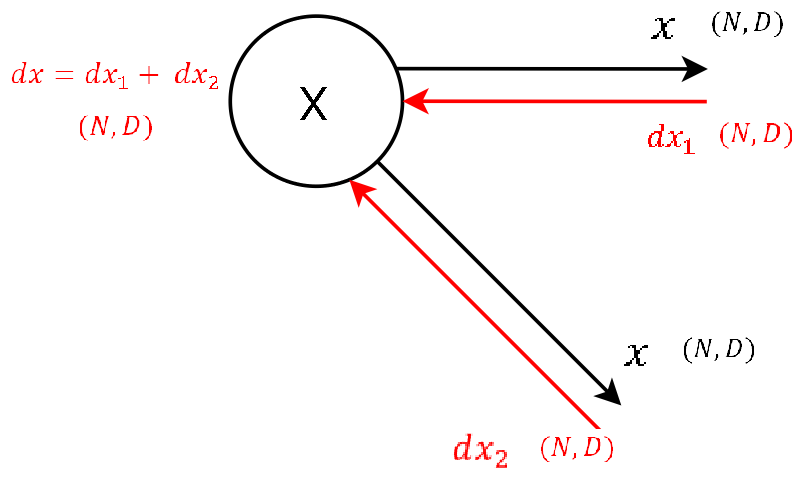
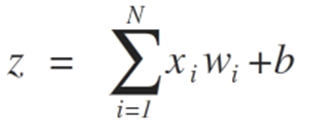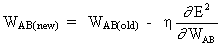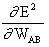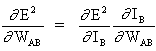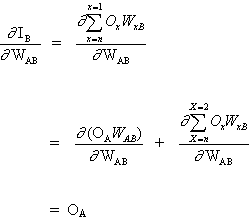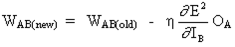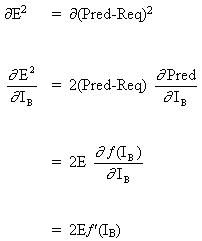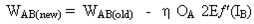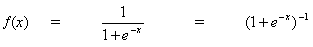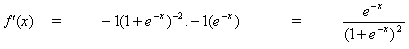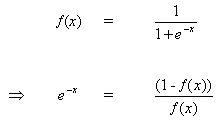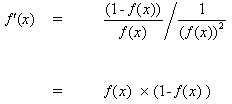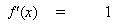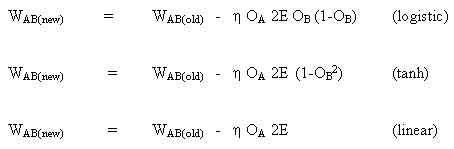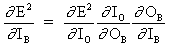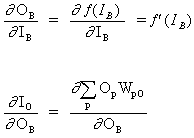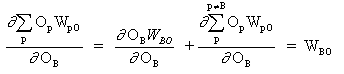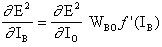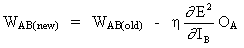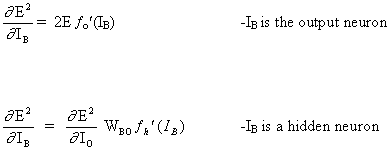Для чего нужен backward pass в нейросети

Deep Learning: как это работает? Часть 3 — архитектуры CNN

В этой статье вы узнаете:

ILSVRC

The ImageNet Large Scale Visual Recognition Challenge — это такое ежегодное соревнование, на котором ресечеры сравнивают свои сетки в задачах обнаружения и классификации объектов на фотографиях.

Это соревнование являлось толчком для развития:

— Архитектур нейронных сетей
— личных методов и практик, которыми пользуются и по сей день

По этому графику видно, как развивались алгоритмы классификации с течением времени:

По оси x — года и алгоритмы (с 2012 года — сверточные нейронные сети).
По оси y — процент ошибок на выборке из top-5 error.

Top-5 error — это способ оценивания модели: модель возвращает некое распределение вероятностей и если среди топ-5 вероятностей есть истинное значение (метка класса) класса, то ответ модели считается правильным. Соответственно, (1 — top-1 error) — это всем знакомая точность (accuracy).

Архитектуры CNN

LeNet-5

Появилась аж в 1998 году! Была предназначена для распознавания рукописных букв и цифр. Под subsampling (понижение размерности) здесь подразумевается pooling-слой.

CONV 5×5, stride = 1
POOL 2×2, stride = 2
CONV 5×5, stride = 1
POOL 5×5, stride = 2
FC (120, 84)
FC (84, 10)

Сейчас эта архитектура имеет только историческую значимость. Подобную архитектуру легко имплементировать «ручками» в любом современном фреймворке для глубокого обучения.

AlexNet

Картинка не дублируется. Так изображена архитектура, потому что архитектура AlexNet тогда не влезала на одно устройство GPU, поэтому «половина» сети работала на одной GPU, а вторая — на другой.

Появилась в 2012 году. С нее и начался прорыв в том самом ILSVRC — она победила все stat-of-art модели того времени. После этого люди поняли, что нейронные сети действительно работают 🙂

Архитектура более конкретно:

Если приглядеться на архитектуру AlexNet, то можно увидеть, что за 14 лет (с появления LeNet-5) не произошло почти никаких изменений, кроме кол-ва слоев.

VGGNet

Появилась в 2014 году.

Две версии — VGG16 и VGG19. Основная идея — использовать вместо больших сверток (11×11 и 5×5) маленькие свертки (3×3). Интуиция в использовании больших сверток простая — мы хотим получать больше информации от соседних пикселей, но гораздо лучше использовать маленькие фильтры чаще.

— Во время обучения нейронной сети для алгоритма обратного распространения ошибки важно сохранять представления объекта (для нас — исходного изображения) на всех этапах (свертках, пулингах) прямого распространения (forward pass — это когда мы подаем на вход картинку и движемся к выходу, к результату). Такое представления объекта может дорого стоить в плане памяти. Взгляните:

Получается примерно 96 МБ на изображение — и это только для forward pass’а. Для backward pass’a (bwd на картинке) — во время вычисления градиентов — примерно в два раза больше. Выходит такая интересная картина: наибольшее число обучаемых параметров расположено в полносвязных слоях, а наибольшую память занимают представления объекта после сверточных и пулинговых слоев. С — синергия.

— Сеть имеет 138 миллионов обучаемых параметров в вариации 16-ти слоев и 143 миллиона параметров в вариации 19-ти слоев.

GoogLeNet

Появилась в 2014 году.

Красные кружочки — это так называемый Inception module.

Давайте взглянем на него поближе:

Мы берем карту признаков (feature map) с предыдущего слоя, применяем к ней какое-то количество сверток с разными фильтрами, потом конкатенируем полученное. Интуиция простая: мы хотим получить различные представления нашей карты признаков, используя фильтры разных размеров. Свертки 1×1 используются для того, чтобы не так сильно наращивать кол-во каналов после каждого такого inception-блока. Т.е. когда у карты признаков большое кол-во каналов, и хотят уменьшить это кол-во, не изменяя высоту и ширину карты признаков, используют свертку размерности 1×1.

Также в сети присутствуют три блока-классификатора, вот так выглядит один из них (тот что справа для нас):

С помощью такой конструкции градиент «лучше» доходит от выходных слоев до входных во время обратного распространения ошибки.

Зачем нужны еще два лишних выхода сети? Дело все в так называемой проблеме затухающего градиента (vanishing gradient problem):

Суть в том, что при выполнении обратного распространения ошибки градиент банально стремится к нулю. Чем глубже сеть — тем она более подвержена этому явлению. Почему так происходит? Когда мы выполняем backward pass, мы идем от выхода ко входу, вычисляя градиенты сложных функций. Производная сложной функции (chain rule) — это, по сути, умножение. И вот так, умножая какие-то значения по пути от выхода ко входу, мы встречаем числа, которые близки к нулю, и, как следствие, веса нейронной сети практически не обновляются. Частично это проблема функций активаций типа sigmoid, у которых выход лежит в каком-то фиксированном диапазоне. Ну и частично эта проблема решается путем использования функции активации ReLu. Почему частично? Потому что никто не дает гарантии на значения обучаемых параметров и представления входного объекта во всех картах признаков.

ResNet

Архитектура (вариант ResNet-34):

Появилась в 2015 году.

Основным новшеством стало большое количество слоев и, так называемые, residual блоки. Эти блоки используются в качестве борьбы с проблемой затухающего градиента. Связь между такими residual-блоками называется shortcut (стрелочки на картинке). Теперь по этим шорткатам градиент и будет доходить до всех нужных параметров, тем самым обучая сеть 🙂

Проблема затухающего градиента актуальна для всех глубоких нейронных сетей.
Существует и ее антагонист — проблема взрывающегося градиента (exploding gradient problem), которая также актуальная для всех глубоких нейронных сетей. Суть понятная из названия — градиент становится слишком большим, что вызывает NaN (not a number, бесконечность). Решение очевидно — ограничить значение градиента, в противном случае — уменьшить его значение (нормировать). Такая техника называется «clipping».

Заключение

В 2019-м году появилась статья о новом семействе архитектур — EfficientNet.

Следить за последними трендами в различных задачах и областях, связанными с Machine Learning, рекомендую тут. На этом ресурсе можно выбрать задачу(например, image classification) и датасет(например, ImageNet) и посмотреть на качество тех или иных архитектур, дополнительную информацию о них. Например, сетка FixEfficientNet-L2 занимает почетное первое место по классификации изображений на датасете ImageNet (top-1 accuracy).

В следующих статьях поговорим про transfer learning, object detection, segmentation.

Источник

Understanding the backward pass through Batch Normalization Layer

Batch Normalization

Btw: it’s called “Batch” Normalization because we perform this transformation and calculate the statistics only for a subpart (a batch) of the entire trainingsset.

Backpropagation

In this blog post I don’t want to give a lecture in Backpropagation and Stochastic Gradient Descent (SGD). For now I will assume that whoever will read this post, has some basic understanding of these principles. For the rest, let me quote Wiki:

Backpropagation, an abbreviation for “backward propagation of errors”, is a common method of training artificial neural networks used in conjunction with an optimization method such as gradient descent. The method calculates the gradient of a loss function with respect to all the weights in the network. The gradient is fed to the optimization method which in turn uses it to update the weights, in an attempt to minimize the loss function.

Uff, sounds tough, eh? I will maybe write another post about this topic but for now I want to focus on the concrete example of the backwardpass through the BatchNorm-Layer.

Computational Graph of Batch Normalization Layer

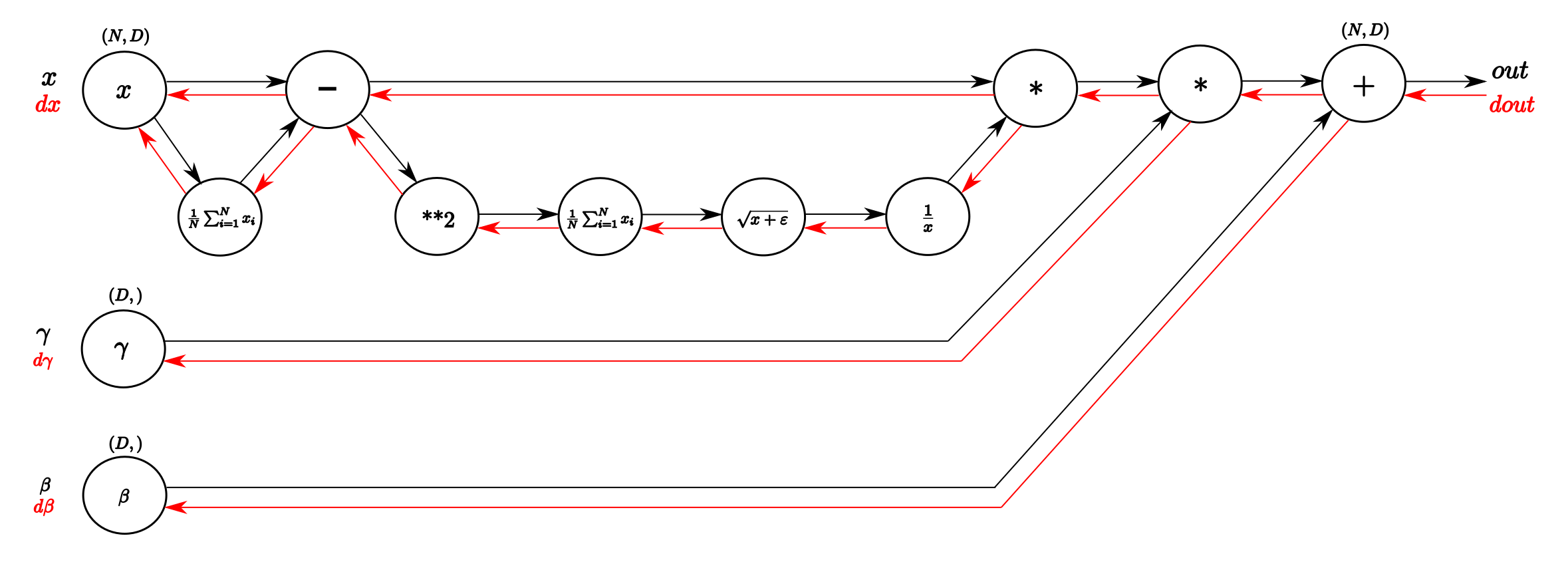
I think one of the things I learned from the cs231n class that helped me most understanding backpropagation was the explanation through computational graphs. These Graphs are a good way to visualize the computational flow of fairly complex functions by small, piecewise differentiable subfunctions. For the BatchNorm-Layer it would look something like this:

A vanilla implementation of the forwardpass might look like this:

Note that for the exercise of the cs231n class we had to do a little more (calculate running mean and variance as well as implement different forward pass for trainings mode and test mode) but for the explanation of the backwardpass this piece of code will work. In the cache variable we store some stuff that we need for the computing of the backwardpass, as you will see now!

The power of Chain Rule for backpropagation

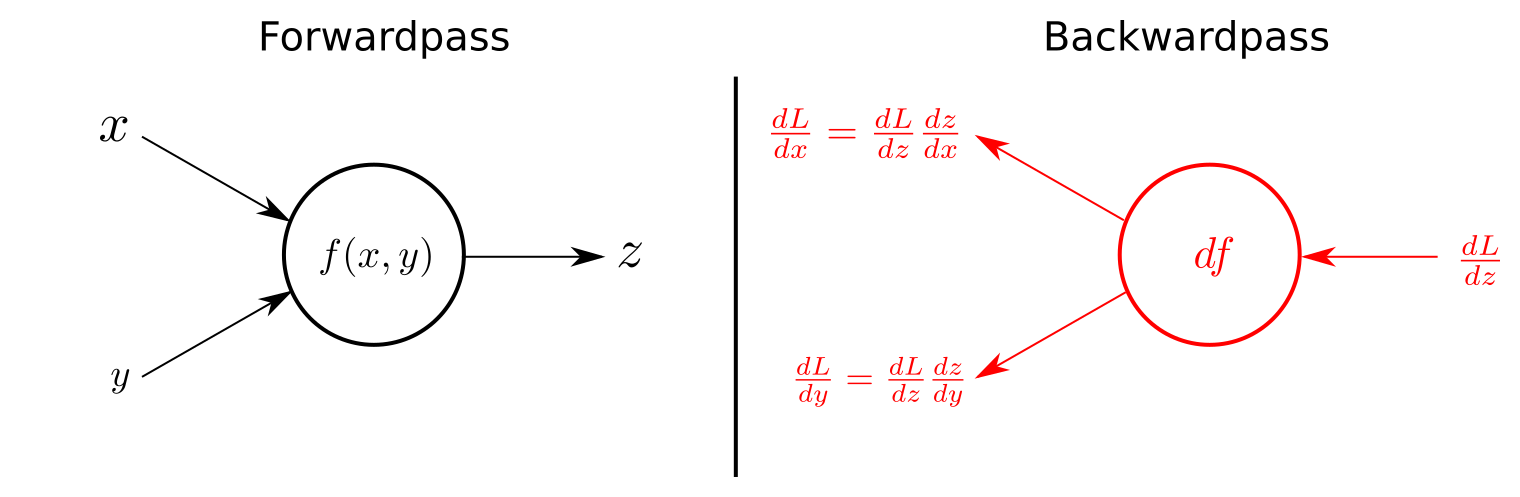
For all who kept on reading until now (congratulations!!), we are close to arrive at the backward pass of the BatchNorm-Layer. To fully understand the channeling of the gradient backwards through the BatchNorm-Layer you should have some basic understanding of what the Chain rule is. As a little refresh follows one figure that exemplifies the use of chain rule for the backward pass in computational graphs.

So again, we only have to multiply the local gradient of the function with the gradient of above to channel the gradient backwards. Some derivatives of some basic functions are listed in the course material. If you understand that, and with some more basic knowledge in calculus, what will follow is a piece of cake!

Finally: The Backpass of the Batch Normalization

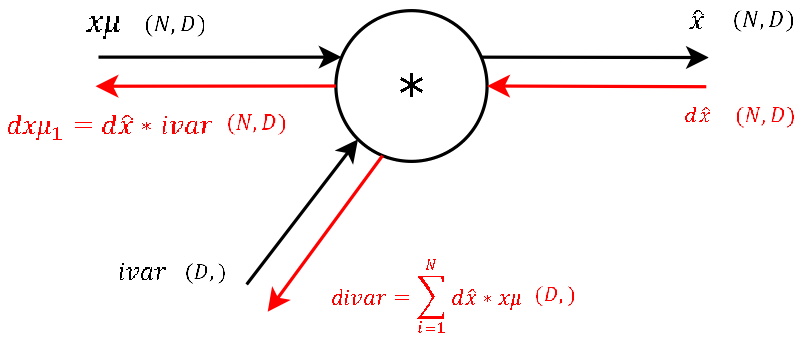
In the comments of aboves code snippet I already numbered the computational steps by consecutive numbers. The Backpropagation follows these steps in reverse order, as we are literally backpassing through the computational graph. We will know take a more detailed look at every single computation of the backwardpass and by that deriving step by step a naive algorithm for the backward pass.

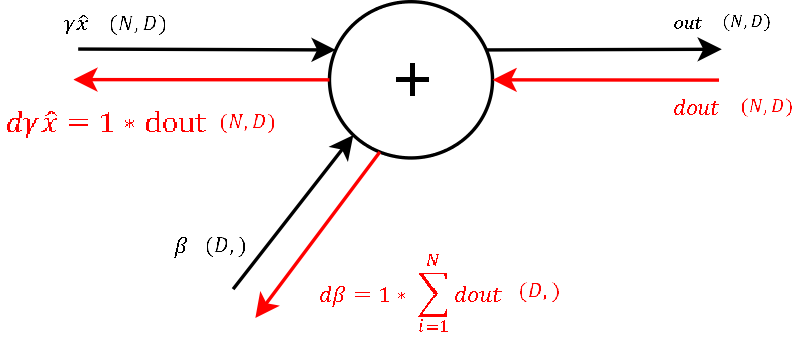
Step 9

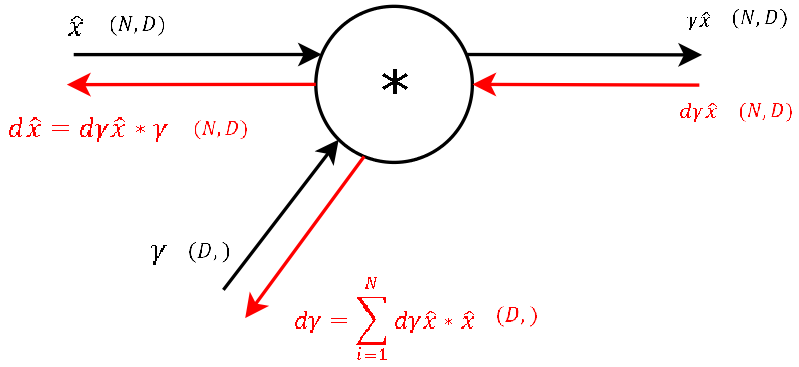
Step 8

Step 7

It’s basically the exact same operation, so lets not waste much time and continue. The two needed variables xmu and ivar for this step are also stored cache variable we pass to the backprop function. (And again: This is one of the main advantages of computational graphs. Splitting complex functions into a handful of simple basic operations. And like this you have a lot of repetitions!)

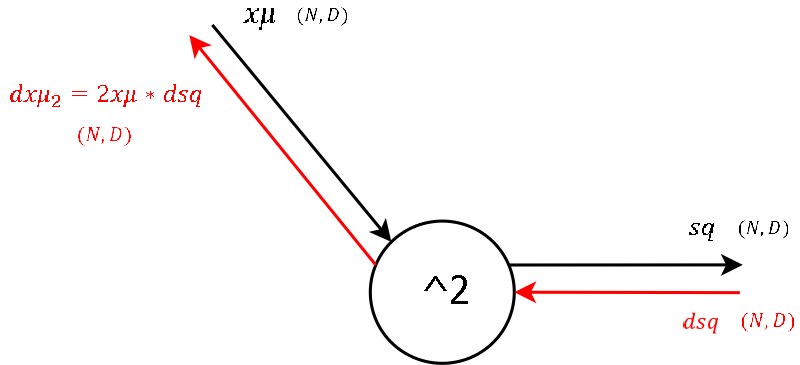
Step 6

Step 5

Step 4

The calculation of the derivative of this steps local gradient might look unclear at the very first glance. But it’s not that hard at the end. Let’s recall that a normal summation gate (see step 9) during the backward pass only transfers the gradient unchanged and evenly to the inputs. With that in mind, it should not be that hard to conclude, that a column-wise summation during the forward pass, during the backward pass means that we evenly distribute the gradient over all rows for each column. And not much more is done here. We create a matrix of ones with the same shape as the input sq of the forward pass, divide it element-wise by the number of rows (thats the local gradient) and multiply it by the gradient from above.

Step 3

I think for all who followed until here, there is not much to explain regarding the derivative of the local gradient.

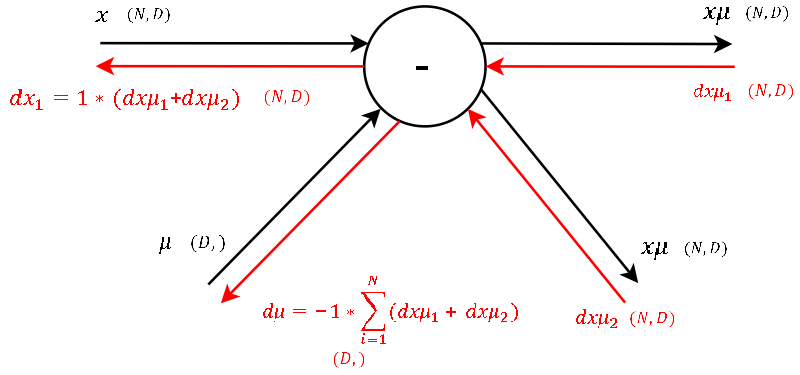
Step 2

Okay lets see. One of the definitions of backprogatation and computational graphs is, that whenever we have two gradients coming to one node, we simply add them up. Knowing this, the rest is little magic as the local gradient for a subtraction is as hard to derive as for a summation. Note that for mu we have to sum up the gradients over the dimension N (as we did before for gamma and beta ).

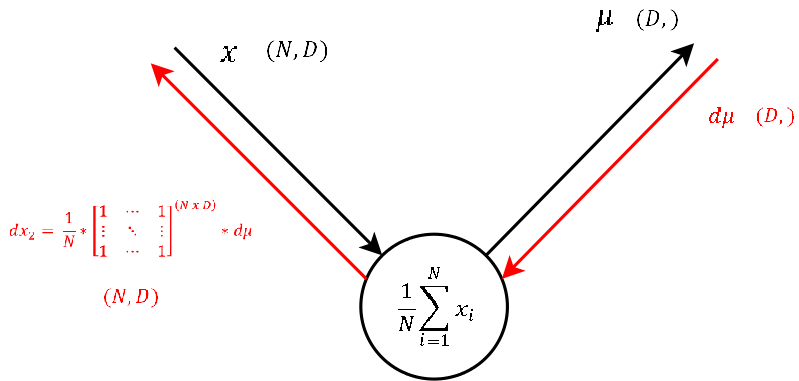
Step 1

As this node executes the exact same operation as the one explained in step 4, also the backpropagation of the gradient looks the same. So let’s continue to the last step.

Naive implemantation of the backward pass through the BatchNorm-Layer

Putting together every single step the naive implementation of the backwardpass might look something like this:

Note: This is the naive implementation of the backward pass. There exists an alternative implementation, which is even a bit faster, but I personally found the naive implementation way better for the purpose of understanding backpropagation through the BatchNorm-Layer. This well written blog post gives a more detailed derivation of the alternative (faster) implementation. However, there is a much more calculus involved. But once you have understood the naive implementation, it might not be to hard to follow.

Some final words

First of all I would like to thank the team of the cs231n class, that gratefully make all the material freely available. This gives people like me the possibility to take part in high class courses and learn a lot about deep learning in self-study. (Secondly it made me motivated to write my first blog post!)

And as we have already passed the deadline for the second assignment, I might upload my code during the next days on github.

Источник

Обратное распространение упрощено

Дата публикации Jul 14, 2019

Этот пост объясняет, что является, вероятно, самой базовой реализацией обратного распространения. Я предполагаю, что читатель имееттвердое теоретическое пониманиеобратного распространения (+ градиентный спуск) и просто не понимает, как начать его реализацию.

Но, к сожалению, это случается не слишком часто. Вот почему так важно понимать back-prop. Лично для меня, с тех пор как я сам реализовал обратную поддержку, у меня был гораздо более высокий уровень успеха, когда мои нейронные сети делали то, что я хочу, чтобы они делали в первые несколько попыток. У Андрея Карпати отличныйстатьяОб этом вы должны обязательно посмотреть. Достаточно убедительно, давайте начнем.

Изображение выше объясняет алгоритм с точки зрения одного нейрона. Вот,Lявляется значением стоимости для прогнозов, сделанных в предыдущем проходе вперед. Градиент (δL / δz) получен этим нейроном из слоев перед ним в сети. Из этого изображения мы получаем, что локальные градиенты (δz /? xа такжеδz / δy), выходы (Z) и активаций (Икса такжеY) для каждого нейрона необходимо сохранить в памяти для последующего расчета. Они используются для расчета градиентов (δL /? xа такжеδL / δy) пройти назад, что получат нейроны предыдущих слоев. Как именно это делается, дается в разделах ниже.

Имена переменных говорят сами за себя и префикс ofd_»перед переменной указывает, что она хранит производную переменной после followingd_’(‘d_this’хранит градиент ‘это’).

Инициализация параметра

Первым делом, прежде чем начать, нужно инициализировать значения параметров для нашей сети. Веса и смещения для разных слоев будут сохранены в виде пар ключ-значение в отдельных словарях. Это довольно просто и может быть сделано с помощью следующего фрагмента кода:

Функция стоимости и метрики

Следующее, что нужно сделать, это сформулировать функцию потерь и найти метрику для проверки производительности нашей сети на каждом прямом проходе. Мы будем использовать простую двоичную кросс-энтропийную потерю в качестве функции стоимости и точность в качестве метрики оценки. Это довольно легко рассчитать и сделать это можно следующим образом:

«get_class_from_probs”- это служебная функция, используемая для получения предсказанных значений класса (0 или 1) вместо вероятностей, полученных из сигмоидальной функции.

Активации и производные

‘d_initПараметр ’- градиент инициализации. Для последнего слоя это значение будет равно 1, а значение будет кумулятивным произведением градиентов до текущего слоя для всех предыдущих слоев.

Форвард Пасс

Это простая часть, где мы выполняем умножение матриц, добавляем смещения на каждом этапе, проводим выходные данные через функцию активации и получаем наш конечный результат. Код делится на две части: однослойный прямой проход и весь прямой проход. Код для прямого прохода одного уровня приведен ниже. Параметры для слоя, состоящего из n нейронов:

Следующим шагом является создание всего прямого прохода с использованием предыдущей функции, код которой приведен ниже. Ключ здесь ксохранить значения выходовиз этого слоя в словарях, как до, так и после прохождения через функцию активации. Это потребуется при передаче градиентов назад с использованием правила цепочки. Параметры:

Обратный проход

Это самая сложная часть здесь. Это также, как и прямой проход, можно разбить на однослойный проход и общий обратный проход. Обратный проход в один слой включает несколько шагов:

Обратите внимание на использованиеПравило цепидля расчета градиентов. Ниже приведен фрагмент кода со следующими параметрами:

Теперь, когда у нас есть средства для вычисления градиентов из одного слоя, мы можем легко поддержать в сети, многократно используя эту функцию для всех слоев в нашей нейронной сети с прямой связью (очевидно, в обратном порядке). Градиенты, рассчитанные с помощью функции one_layer_backward_pass, сохраняются в ‘градиенты‘ толковый словарь. Эти градиенты будут позже использоваться для обновления параметров (веса + смещения) при выполнении градиентного спуска.

Примечание: градиент функции потерь относительно прогнозов, сделанных сетью, должен быть рассчитан вне основного цикла. Это было сделано в строке 10 фрагмента ниже Тривиально придумать эту формулу, взяв производную от ‘cross_entropy_loss’Функция (параметризованная прогнозами и фактическими метками) относительно прогнозов‘y_pred»,

Важные вещи, чтобы отметить здесь:

Обновление параметров и обучение

Трудная часть сделана! Теперь все, что нам нужно сделать, это обновить параметры и обучить сеть, используя градиентный спуск. В этом игрушечном примере мы будем использовать пакетный градиентный спуск, но вам лучше использовать мини-пакетный градиентный спуск для эффективности, когда данных об обучении много. Веса и смещения обновляются с помощью следующей функции. Параметры:

Наконец, сеть можно обучить, используя следующие шаги:

Вот код для обучения сети:

Это оно! Это действительно так просто. Теперь осталось только проверить нашу сеть на наличие невидимых данных. Для более глубокого понимания важно попробовать это самостоятельно, выполнить математику и вычисления в своей голове и посмотреть на размеры градиентов, весов и смещений на разных этапах сети. Это ключ, чтобы не запутаться между подпоркой и градиентным спуском. Back-prop используется только для вычисления градиентов на разных этапах сети, тогда как спуск по градиентам использует эти градиенты для обновления параметров сети. Я опускаю тестовый код здесь (по сути, только один проход вперед), но вы можете посмотреть на мою полную реализациюВот(включая разделение валидации поездов и тестирование сети). Спасибо за проделанную работу!

Источник

Многослойный перцептрон и алгоритм обратного распространения ошибки

Введение

Краткий обзор истории

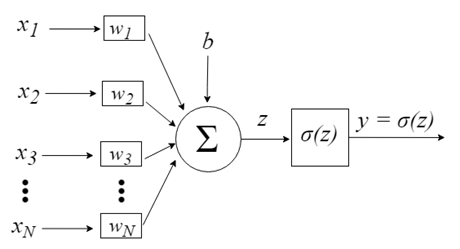
Компьютерная модель нейрона: перцептрон

Перцептрон

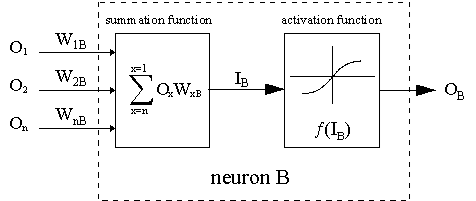
Перцептрон вдохновлен идеей обработки информации единственной нервной клетки, называемой нейроном. Нейрон принимает на вход сигналы через свои дендриты, которые передают электрический сигнал телу клетки. Точно так же перцептрон получает входные сигналы из примеров обучающих данных, которые предварительно взвесили и объединили в линейное уравнение, называемое активацией.

Где weight — это вес сети, X — это входное значение, i — индекс веса или входные данные, а смещение — это специальный вес, который не имеет множитель в виде входного значения (можем считать, что входные данные всегда равны 1.0).

Затем активация преобразуется в выходное (прогнозируемое) значение с помощью передаточной функции (функция активации).

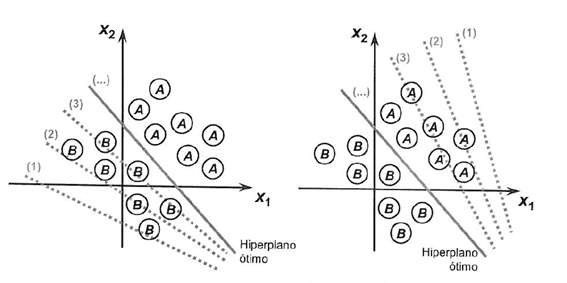
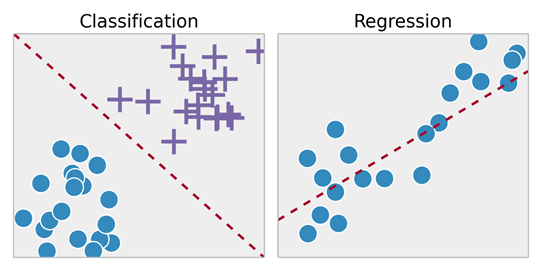
Таким образом, перцептрон представляет собой алгоритм классификации проблем с двумя классами (двоичный классификатор), где для разделения двух классов может использоваться линейное уравнение.

Это тесно связано с линейной регрессией и логистической регрессией, которые осуществляют прогнозы аналогичным образом (например, взвешенная сумма входов).

Алгоритм перцептрона — простейший вид искусственной нейронной сети. Это модель одного нейрона, которая может использоваться в задачах классификации двух классов и обеспечивает основу для дальнейшего развития гораздо более крупных сетей.

Чтобы проиллюстрировать процесс, направленный на достижение предела разделимости классов, ниже мы показываем две ситуации, которые демонстрируют их сближение к стабилизации с учетом только двух входов

Веса алгоритма перцептрона следует оценивать на основе данных обучения с использованием стохастического градиентного спуска.

Стохастический градиент

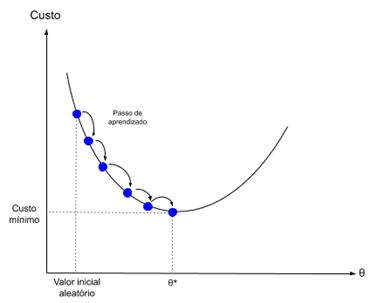
Градиентный спуск — это процесс минимизации функции в направлении градиента функции стоимости.

Это подразумевает знание формы стоимости, а также производной, чтобы с определенной точки мы могли узнать наклон и могли двигаться в этом направлении, например, вниз по направлению к минимальному значению.

В машинном обучении мы можем использовать метод, который оценивает и обновляет веса для каждой итерации, называемый стохастическим градиентным спуском, чтобы минимизировать ошибку модели в наших обучающих данных.

Принцип работы этого алгоритма оптимизации заключается в том, что каждый обучающий экземпляр показывается модели по одному. Модель делает прогноз для обучающего экземпляра, вычисляет ошибку и обновляет модель, чтобы уменьшить ошибку для следующего прогноза.

Эту процедуру можно использовать для поиска набора весов в модели, который дает наименьшую ошибку для модели в обучающих данных.

Для алгоритма перцептрона на каждой итерации веса w обновляются с использованием уравнения:

Для стохастического градиентного спуска требуются два параметра:

Они вместе с обучающими данными будут аргументами для функции.

Нам нужно выполнить 3 цикла в функции:

1. Цикл для каждой эпохи.

2. Цикл для каждой строки в обучающих данных для эпохи.

3. Цикл для каждого веса, который обновляется для одной строке в одной эпохи.

Веса обновляются в зависимости от ошибки, допущенной моделью. Ошибка рассчитывается как разница между фактическим значением и прогнозом, сделанным с помощью весов.

Для каждого входного атрибута есть свой вес, и они постоянно обновляются, например:

Смещение обновляется аналогичным образом, только без входа, поскольку оно не связано с конкретным входным значением:

Применение модели нейрона:

Теперь перейдем к практическому применению.

Этот урок разделен на 2 части:

2. Оптимизация веса сети

Эти шаги обеспечат основу для реализации и применения алгоритма перцептрона к другим задачам классификации.

Нам нужно определить количество столбцов в нашем наборе X, для этого мы определяем константу

В MQL5 многомерный массив может быть статическим или динамическим только для первого измерения, а поскольку все остальные измерения будут статическими, при объявлении массива необходимо указать размер.

Это будет необходимо как при оценке значений весов кандидатов при стохастическом градиентном спуске, так и после завершения модели. Прогнозы надо делать и на тестовых данных, и на новых.

Первый вес всегда является смещением, поскольку он автономен и не работает с конкретным входным значением.

Перенос нейронов:

Как только нейрон активирован, нам нужно передать активацию, чтобы увидеть, каковы на самом деле выходные данные нейрона.

Мы получаем в качестве аргумента в функции прогнозирования входной набор X, массив с весами (W) и строку, для которой прогнозируется входной набор X.

Мы можем придумать небольшой набор данных, чтобы проверить нашу функцию прогнозирования.

Мы также можем использовать заранее подготовленные веса, чтобы делать прогнозы для этого набора данных.

После того, как мы собрали все это вместе, мы можем протестировать нашу функцию прогнозирования ниже.

activation = (w1 * X1) + (w2 * X2) + b

Или с конкретными значениями веса, мы вручную выбираем как:

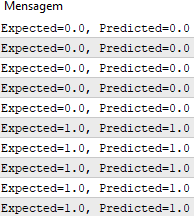
После завершения работы функции мы получаем прогнозы, которые соответствуют ожидаемым выходным значениям y .

Теперь можем реализовать стохастический градиентный спуск для оптимизации значений веса.

2. Оптимизируем веса сети

Веса для наших обучающих данных можно оценить, используя стохастический градиентный спуск, как было сказано ранее.

Ниже приведена функция train_weights(), которая вычисляет значения веса для набора обучающих данных с использованием стохастического градиентного спуска.

В MQL5 мы не можем получить возврат из этого массива с данными обученных весов, потому что, в отличие от переменных, массивы могут быть переданы в функцию только по ссылке. Это означает, что функция не создает собственный экземпляр массива, а вместо этого работает напрямую с переданным ей массивом. Таким образом, все изменения, осуществляемые в этом массиве внутри функции влияют на исходный массив.

На каждой эпохе мы отслеживаем сумму квадратичной ошибки (положительное значение), чтобы отслеживать уменьшение ошибки. Жто позволяет наблюдать как алгоритм минимизирует ошибку на каждой эпохе.

Давайте протестируем нашу функцию с одним и тем же набором данных, представленным выше.

Мы используем скорость обучения 0,1 и обучаем модель только для 5 эпох или 5 показов весов для всего набора обучающих данных.

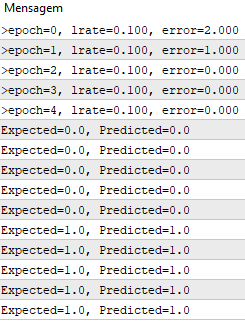
При выполнении примера для каждой эпохи печатается сообщение с суммой квадратичной ошибки для этой эпохи и окончательным набором весов.

Мы видим, как быстро алгоритм выучивает проблему.

Этот тест можно найти в файле PerceptronScript.mq5.

Многослойный перцептрон

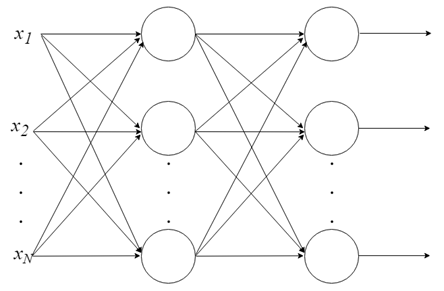
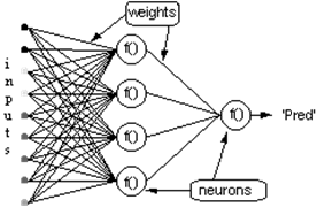
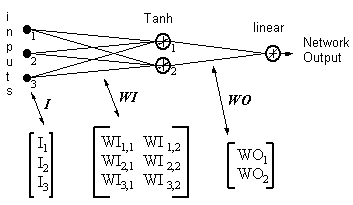
С одним нейроном мало что можно сделать, но мы можем объединить их в многоуровневую структуру, каждый с разным количеством нейронов, и сформировать нейронную сеть, называемую многослойным перцептроном (« multi layer perceptron, MLP »). Вектор входных значений X проходит через начальный слой, выходные значения которого связаны со входами следующего уровня, и так далее, пока сеть не предоставит выходные значения последнего слоя в качестве результата. Сеть может быть организована в несколько слоев, что делает ее глубокой и способной выучить все более сложные отношения.

Обучение MLP

Для того, чтобы такая сеть работала, ее нужно обучать. Это как учить ребенка читать. Обучение MLP происходит в контексте машинного обучения с учителем, но как это работает?

Обучение с учителем:

Обратное распространение

Разве мы не учимся на ошибках?

Идея алгоритма обратного распространения ошибки состоит в том, чтобы на основе расчетной ошибки, полученной на выходном слое нейронной сети, пересчитать значение весов вектора W последнего слоя нейронов. Затем мы переходим к предыдущему слою и так далее, от конца к началу, то есть, он состоит из обновления всех весов W слоев, от последнего до достижения входного слоя сети путем обратного распространения ошибки, полученной сетью. Другими словами, ошибка вычисляется между тем, что предсказала сеть, и тем, что она была на самом деле (фактический 1, предсказанный 0; у нас есть ошибка!), поэтому мы пересчитываем значения всех весов, начиная с последнего слоя и переходя к первому, всегда обращая внимание на уменьшение этой ошибки.

Алгоритм обратного распространения ошибки состоит из двух этапов:

1. Прямой проход («forward pass»), при котором наши входы проходят через сеть и получают прогнозы выхода (этот шаг также известен как фаза распространения).

2. Обратный проход («backward pass»), при котором мы вычисляем градиент функции потерь на последнем слое (то есть слое прогнозирования) сети и используем этот градиент для рекурсивного применения цепного правила («chain rule») для обновления весов в нашей сети (также известного как стадия обновления веса или обратное распространение)

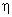
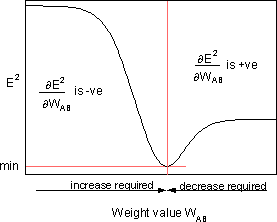
где — параметр скорости обучения, который определяет скорость обучения, а

является чувствительностью ошибки E² к весу W AB и определяет направление поиска в пространстве весов для нового веса W AB (новый), как изображено на рисунке ниже.

Чтобы минимизировать E², правило дельты обеспечивает необходимое направление изменения веса.

Возможны две ситуации:

Рассмотриваем первый случай:

Поскольку B является выходным нейроном, изменение квадрата ошибки из-за настроки W AB просто является изменением квадрата ошибки выходного сигнала B.

объединяя уравнение (5) и уравнение (6), получаем

Правило изменения весов, когда нейрон B является выходным нейроном, если выходная функция активации, f (.), является логистической функцией:

Дифференцируем уравнение (8) по аргументу x:

при вставке (10) в (9) получаем:

таким же образом для функции tanh

или для линейной функции (identity)

Рассматривая второй случай :

B это скрытый нейрон

где O представляет выходной нейрон

где p это индекс, который охватывает все нейроны, включая нейрон B, который обеспечивает входные сигналы для выходного нейрона. Расширяем правую часть уравнения (13),

При вставке (13) и (13) в (12):

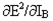
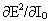
Следовательно, теперь это выражается как функция от , вычисляемая, как описано в уравнении (6).

Полное правило изменения веса W AB между нейроном A, который посылает сигнал нейрону B, является таким:

где fo (.) и fh (.) это скрытые функции активации и выхода соответственно.

Пример

LR = коеффициент обучения

Обновления веса становятся

нейроном с линейным выходом

Этот урок разделен на 5 частей:

1. Инициализация сети.

2. Прямое распространение (FeedForward).

3. Обратное распространение.

Для нашей разработки мы реализуем применение на чистом MQL. Нам уже известно, что существуют библиотеки на других языках, которые уже являются гораздо более сложными, и настоятельно рекомендуется использовать их из практических соображений и соображений производительности, но, как уже было сказано в начале, важно понимать внутреннее устройство таких библиотек, чтобы иметь больший контроль над всем процессом. Мы также не использовали ООП в нашем тесте, поскольку это всего лишь алгоритм для иллюстрации предыдущих уравнений, в нем нет необходимости. Однако в реальных случаях гораздо практичнее использовать ООП, поскольку оно обеспечивает масштабируемость проекта.

1. Инициализация сети

У каждого нейрона есть набор весов, которые необходимо поддерживать. Вес для каждого входного соединения и дополнительный вес для смещения.

Рекомендуем инициализировать веса сети для небольших случайных чисел. В этом случае мы будем использовать случайные числа в диапазоне от 0 до 1. Для этого мы создали функцию для генерации случайных чисел.

Ниже представлена ​​функция под названием initialize_network(), которая создает веса нашей нейронной сети.

3. Обратное распространение

Алгоритм обратного распространения назван в честь способа обучения весов

Ошибка вычисляется между ожидаемыми выходами и выходными сигналами сети прямого распространения. Затем эти ошибки передаются обратно по сети от выходного слоя к скрытому слою, перекладывая ответственность за ошибку и обновляя веса по мере их поступления.

Математика ошибки обратного распространения была объяснена выше.

Сеть обучается методом стохастического градиентного спуска.

Это включает в себя несколько итераций, раскрывающих набор обучающих данных в сети, и для каждой строки данных прямое распространение входных данных, обратное распространение ошибки и обновление весов сети.

Делать прогнозы с помощью обученной нейронной сети довольно просто.

Мы уже видели, как распространить паттерн входа для получения выходных данных. Это все, что нам нужно сделать, чтобы осуществить прогноз. Мы можем использовать выходные значения напрямую как вероятность принадлежности паттерна к каждому выходному классу.

Полный пример можно найти в файле MLP_Script.mq5.

Заключение

Мы занимались вычислениями, задействованными в процессе развития нейрона перцептрона, а также сети нейронов перцептрона, называемой «multi layer perceptron, MLP». В данном процессе мы поняли, как осуществляется обучение этого типа сетей с использованием обратного распространения ошибки и градиентного спуска.

Источник