Для чего нужен бинарный поиск

Бинарный поиск

Линейный поиск

Мы считаем, что вы уже знаете линейный поиск, а именно умеете решать задачи такого типа:

Задание

Убедитесь, что вы умеете решать эти задачи. Докажите, что быстрее, чем O(n) их решить в худшем случае нельзя.

Бинарный поиск

Однако иногда найти число X в массиве можно и быстрее! Для этого надо добавить условие на то, что массив отсортирован. Но давайте начнем не с этого.

Задание

Я загадал число X от 1 до 100. Вы можете спрашивать, больше ли мое число чем число T, я отвечаю “да” или “нет”. За сколько вопросов в худшем случае вы сможете найти число X? Как нужно действовать?

Почему нужно делить обязательно пополам? Почему бы не спросить “число X больше, чем 80?” первым же вопросом? Но если вдруг ответ “нет”, то мы останемся с 80 вариантами вместо 100. То есть деление отрезка ровно пополам гарантирует, что в худшем случае мы останемся не более чем с половиной вариантов.

Теперь вернёмся к нашей задаче. Можно понять, что такой алгоритм работает как раз за \(O(\log n)\) вопросов (если число 100 на заменить абстрактную переменную \(n\) ). Несложно убедиться, что именно логарифм раз нужно поделить число на два, чтобы получилось 1.

Общий принцип

А теперь представьте такую задачу: у вас есть массив, состоящий из некоторого количества подряд идущих нулей, за которыми следует какое-то количество подряд идущих единиц.

Вам дан массив, и вам нужно найти позицию первой единицы, то есть найти такое место, где заканчиваются нули, и начинаются единицы. Это можно сделать с помощью линейного поиска за один проход по массиву, но хочется сделать это быстрее.

Есть много способов писать бинарный поиск, и в его написании люди очень часто путаются. Очень удобно в данном случае воспользоваться инвариантом (это слово значит “постоянное свойство”):

Пусть переменная left всегда указывает на \(0\) в массиве, а переменная right всегда указывает на \(1\) в массиве.

Дальше мы будем переменные left и right постепенно сдвигать друг к другу, и в какой-то момент они станут соседними числами. Это и будет означать, что мы нашли место, где заканчиваются нули и начинаются единицы.

Осталось нам написать цикл while :

Мы решили задачу для ноликов и единичек, но это легко обобщается на абсолютно любую задачу, где есть какое-то свойство, которое в начале массива не выполняется, а потом выполняется.

Задание

Поэтому зачастую такие задачи сформулированы таким образом:

Задание

Найдите время работы, за которое решается эта задача?

Источник

Бинарный поиск в C++: подробное руководство

Сегодня мы и изучим его. Также попытаемся ответить на такие вопросы: как бинарный поиск работает в программе, плюсы и минусы его использования у себя в коде и в каких структурах данных можно его применять, а в каких нет. Поехали!

Что такое бинарный поиск

Линейный поиск по сравнению с бинарным — дешевая подделка. Бинарный поиск — очень быстрый алгоритм с не сложной реализацией, который находит элемент с определенным значением в уже отсортированном массиве.

Очень важно помнить! Алгоритм будет работать правильно, только с отсортированным массивом. А если по случайности вы забыли отсортировать массив перед его использованием, то в большинстве случаев тот ответ, который подсчитал алгоритм, будет неверным.

Принцип работы бинарного поиска

Самым легким и самым долгим по времени решением, будет поочередная проверка пассажиров в комнате с прибором (это линейный поиск). Но это слишком долго.

В задаче выше охранники использовали алгоритм двоичного поиска для нахождения диверсанта. В обычной программе принцип работы бинарного поиска такой же, как и в примере, выше.

Как создать бинарный поиск в C++

Давайте посмотрим как работает бинарный поиск на примере.В примере ниже в строке 9 мы создали массив arr на 10 элементов и в строке 12 предложили пользователю с клавиатуры заполнить его ячейки.

В строке 20 мы предлагаем пользователю ввести ключ (который нужно будет найти в массиве), а дальше мы с бинарным поиском проверим массив на наличие введенного ключа пользователем. Если мы найдем ключ в массиве, то выведем индекс ячейки, в которой находится ключ.

Источник

Бинарный поиск

Определение

Часто вместо математической функции \(f(x)\) бинарный поиск производится на отсортированных по возрастанию или убыванию массивах. Если массив не содержит искомого элемента, алгоритм найдёт ближайший к нему элемент (или, более точно, позицию в массиве, на которую нужно вставить искомый элемент, чтобы сохранить упорядоченность).

Алгоритм

Предположим, что наша функция возрастает, и текущие границы промежутка, точно содержащего \(x\), это \([l; r]\). Сужение выполняется следующим образом: возьмём “среднюю” точку в промежутке \(m = \frac<2>\), и сравним \(f(m)\) с \(y\):

Если функция не возрастает, а убывает, алгоритм выглядит практически так же, но логика при сужениях обратная: если \(f(m)

Реализация для отсортированного массива как дискретной функции на C++

Реализации бинарного поиска в стандартной библиотеке C++

В стандартной библиотеке C++ содержатся две основные функции реализующие бинарный поиск на отсортированном массиве. Их определения:

Функция std::upper_bound используется в особых ситуациях, когда нужно найти положение первого элемента, больше заданного.

Возвращаясь к ситуации наличия нескольких искомых элементов в массиве, с помощью этих функций искомый промежуток можно записать следующим образом:

Для бинарного поиска по массиву, отсортированному по собственному компаратору вы можете воспользоваться расширенной формой функций:

Бинарный поиск по ответу

Источник

Использование бинарного поиска для оптимизации запроса на выборку данных

Введение

Сейчас очень популярна тем оптимизации работы с различными СУБД. На многочисленных форумах ведутся дискуссии о «самой лучшей СУБД в мире», но часто все это перетекает в необоснованные выкрики о том, что «я познал смысл жизни и понял, что самое лучшее хранилище данных — Х».

Да, несомненно, сейчас мы можем наблюдать активное развитие NoSQL решений, которые позволяют делать многое. Но данная статья не о них. Так вышло, что я сменил работу и в нагрузку мне достался один очень интересный проект на связке php+MySQL. В нем есть много хороших решений, но он писался без расчёта на большую аудиторию. За несколько лет существования количество активных пользователей начало приближаться к числам с 7 нулями. Так как проект представляет из себя подобие социальной сети с игровыми элементами, то таблица с пользователями оказалась не самой «тяжёлой» из всех. В наследство мне достались таблицы с десятками миллионов вещей пользователей, личных сообщений, биллинговыми записями и т. п. Проект начали рефакторить, разбивать на несколько серверов и достигли значительных результатов. Сейчас все стабильно.

Но недавно мне на почту прислали новую задачу. Суть заключалась в сборе статистики. Проанализировав требования я понял, что для выполнения достаточно написать один единственный запрос, выполняющий 3 INNER JOIN’а на таблицы, размеры которых впечатляли. Каждая таблица в среднем содержала 40 миллионов записей. Получается, что временная таблица состояла бы из 4*4*4*10^21 = 64*10^21 записей. Это колоссальная цифра. И загружать СУБД таким запросом для сбора статистики — непозволительная роскошь.

Далее, собственно, я и хочу представить решение данной абстрактной задачи, которое пришло мне в голову, когда я вспоминал занятия по информатике на первом курсе университета.

(в проекте используется СУБД MySQL, но алгоритм не имеет каких-либо специфических особенностей)

Что такое бинарный поиск

Думаю, что многие из вас писали лабораторные работы, посвящённые поиску элемента в массиве с использование бинарного алгоритма. Постараюсь кратко изложить его суть.

Пусть у нас имеется отсортированный массив из n элементов:

Первый элемент массива = 1
Последний элемент массива = n

Нам необходимо найти индекс элемента со значением f.

Каждый шаг заключается в том, что мы вычисляем середину массива:

Середина массива = round(Первый элемент + Последний элемент)/2

Затем вычисляем значение этого элемента и проверяем больше или меньше полученное значение в сравнении с искомым f. Диапазон поиска уменьшается в 2 раза:

Если > f, то
Последний элемент массива = значение середины
Иначе
Первый элемент массива = значение середины

Данные шаги повторяются пока не наступит одно из условий:

Думаю, суть ясна. Таким образом мы значительно ускоряем поиск нужного элемента за счёт сокращения диапазонов поиска, но жертвуем некоторой точностью вычислений (для статистики это не критично, если пару элементов из миллионов не будут учтены. В противном случае необходимо сделать эпсилон нулевым и завершать поиск только после достижения последнего уровня дерева).

Переходим к практике

Итак, предположим, что нам необходимо сделать INNER JOIN на 3 таблицы, а затем задать условие «столбец х в диапазоне между 10 и 20». Причём столбец х не имеет индекса. Это будет очень долго выполнятся. Тут и приходит на помощь это простой способ.

Берем таблицу с этим самым столбцом и применяем на ней бинарный поиск, для поиска диапазона первичных ключей, удовлетворяющих условию 10 = 10 AND x

Источник

Двоичный поиск

Основные авторы описания: А. В. Чупин.

Синонимы названия метода: двоичный поиск, бинарный поиск, метод деления пополам, метод половинного деления, дихотомия.

Содержание

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод двоичного поиска используется в качестве быстрого варианта поиска в заранее отсортированном массиве. Получил распространение благодаря как наименьшей из возможных высоте алгоритма, так и из-за ряда своих вычислительных характеристик, а также (в среде нечисленных алгоритмов) из-за своей рекурсивности, то есть лёгкости записи.

Основная идея заключается в дроблении массива на половины и дальнейшем рекурсивном поиске в одной из них.

Альтернативой служит метод линейного поиска (то есть полного перебора), имеющий, соответственно, линейную вычислительную сложность ( [math]O(n)[/math] ), однако работающий на произвольно упорядоченных массивах. Если сравнивать возможности применения обоих методов, то линейный поиск выгоднее применять 1) для поиска в коротких массивах; 2) когда требуется провести поиск небольшое число раз; 3) в потоковом случае. В отличие от него, бинарный поиск требует предобработку (сортировку, сложность которой не менее [math]O(n \log_2 n)[/math] ) и особенно полезен, если массив большой и поиск проводится неоднократное (точнее, более, чем порядка [math]O(\log_2 n)[/math] ) число раз.

Метод позволяет различные обобщения и видоизменения:

Вариации также могут касаться формата и сути вывода результата в отдельных случаях (см. варианты возврата при ненахождении).

Очень близко к метод бинарного поиска по массиву стоит непрерывный аналог — метод бисекции (метод деления пополам) нахождения корня непрерывной функции на заданном отрезке. Самое большое отличие заключается в вычислении значения функции вместо нахождения элемента массива по его индексу, а также использование действительных чисел в качестве аргумента в отличие от целых чисел для индексации элементов массива.

По своему определению, алгоритм может быть записан в одной из двух основных форм — рекурсивной и итеративной. Поскольку вычислительное ядро в них одинаковое, но в рекурсивном есть дополнительная нагрузка по вызову функций и хранению их стека, в данной статье рассматривается только итеративная версия.

1.2 Математическое описание алгоритма

Вычисляемые данные: индекс (номер позиции) элемента, равного искомому (или ответ, что такого элемента нет).

1.3 Вычислительное ядро алгоритма

1.4 Макроструктура алгоритма

По определению алгоритм состоит из рекурсивных вызовов самого себя для меньших массивов. Стандартные макрооперации не используются.

1.5 Схема реализации последовательного алгоритма

В рекурсивном варианте определяется функция, принимающая в числе прочих параметров индексы концов отрезка массива, на котором идёт текущий поиск, а операция «идём к шагу 2» означает вызов той же функции поиска с другими индексами концов отрезка.

В итеративном варианте пп. 2-5 обёрнуты в бесконечный цикл, выход из которого возможен либо в п. 2 (как неуспешный), либо в п. 5, когда значение найдено.

1.6 Последовательная сложность алгоритма

Таким образом, алгоритм обладает логарифмической временной сложностью по данным и даже последовательная реализация достаточно быстра и, в принципе, не нуждается в распараллеливании.

1.7 Информационный граф

Граф алгоритма является параметризованным (зависит от размера массива) и недетерминированным (в смысле, что порядок вычислений зависит от начальных данных).

1.8 Ресурс параллелизма алгоритма

1.9 Входные и выходные данные алгоритма

Дополнительные ограничения: массив упорядочен.

Выходные данные: индекс элемента [math]A[/math] в массиве, если он есть.

Объём выходных данных: один скаляр.

1.10 Свойства алгоритма

Алгоритм абсолютно устойчив, так как действия производятся только над целыми числами, и поэтому погрешность всегда равна 0.

2 Программная реализация алгоритма

Возможная простейшая реализация алгоритма на языке C:

Здесь ряд индексов [math]l_k, m_k, r_k[/math] из математической схемы алгоритма превращён в одну переменную, поскольку требуются только последние значения этих рядов.

2.1 Особенности реализации последовательного алгоритма

Обычно в качестве ответа выводят −1, если число не найдено.

Другие возможные варианты в данной ситуации (выбор зависит от того, как и где будет использоваться метод поиска как базовая единица) [8] :

2.1.1 Частые ошибки при реализации

Несмотря на то, что код достаточно прост, в нём есть несколько ловушек, на которые нужно обратить внимание [9] :

2.2 Локальность данных и вычислений

Пространственная локальность достаточно плохая — начальные обращения в память гарантированно далеки друг от друга. Однако расстояние с номером итерации экспоненциально уменьшается и в конце есть надежда на использование преимуществ локальности обращений.

Временная локальность ещё хуже — один и тот же элемент массива никогда не требуется дважды.

2.2.1 Локальность реализации алгоритма

2.2.1.1 Структура обращений в память и качественная оценка локальности

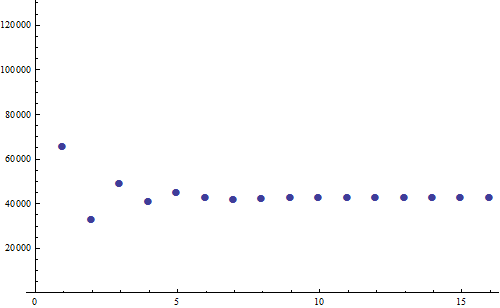
На рис. 3 представлен профиль обращений в память для реализации последовательного алгоритма двоичного поиска. В программе задействован массив и три переменные, на рисунке показаны обращения только к элементам этого массива. Каждая точка соответствует одной итерации алгоритма.

Видно, что на каждой итерации используется одна ячейка памяти, при этом адреса располагаются достаточно хаотично. Пространственная локальность от очень плохой постепенно улучшается до идеальной, когда идут обращения только в близкие ячейки памяти. Данные из массива никогда не используются повторно, поэтому временная локальность плохая.

2.2.1.2 Количественная оценка локальности

2.3 Возможные способы и особенности параллельной реализации алгоритма

Однако при этом потребуется предусмотреть обмен результатами сравнения своей точки деления на каждом процессоре для определения искомого интервала для следующей итерации. Это потребует минимум одной коллективной операции обмена, что ставит под сомнение эффективность распараллеливания.

2.4 Масштабируемость алгоритма и его реализации

2.4.1 Масштабируемость алгоритма

2.4.2 Масштабируемость реализации алгоритма

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

Использовать алгоритм в любой реализации для архитектур с разделённой памятью смысла не имеет — из-за нелокального доступа к исходным данным и малого количества вычислительных операций даже в параллельной модификации выигрыш будет съедаться коммуникациями.

Применение систем с общей памятью с помощью OpenMP теоретически имеет смысл, однако для получения хоть какого-то ускорения требуется выполнение нескольких условий:

30 поискам в массиве из миллиарда элементов).

Источник