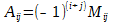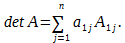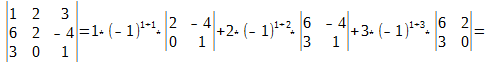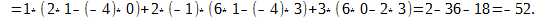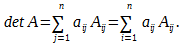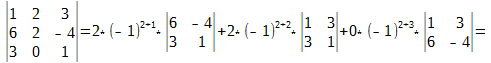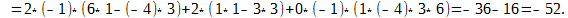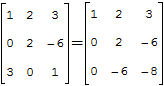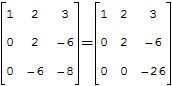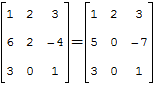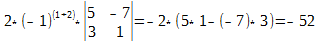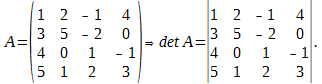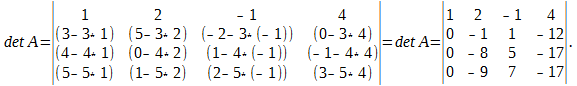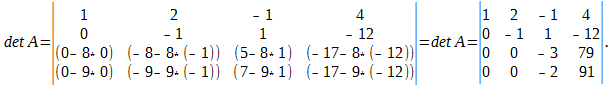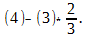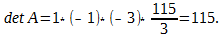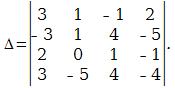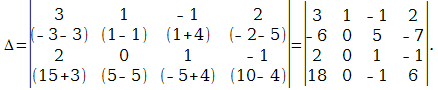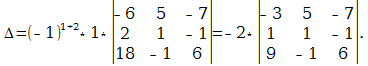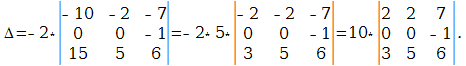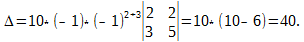Для чего нужен детерминант

Как вычислить определитель (детерминант) матрицы? Минор и алгебраическое дополнение

Без преобразования матрицы, определитель легко посчитать только для матриц размером 2×2 и 3×3. Это делается по формулам:

(можно посчитать по любой строке, выше приводиться формула расчёта определителя по первой строке).

Расчёты для матриц размером 4×4 и выше затруднительны, поэтому их нужно преобразовывать в соответствии со свойствами определителя. Нужно стремиться получить матрицу, в которой все значения кроме одного любого столбца или любой строки равны нулю. Пример такой матрицы:

Для неё определитель равен:

Обратите внимание, что

это вычисление детерминанта матрицы, полученой вычетом строки и столбца, на пересечении которых находиться единственное не нулевое числов строки/столбца, по которому мы разлагаем матрицу:

Если привести матрицу к треугольному виду, то её определитель вычисляется как произведение цифр по диагонали. Например, для матрицы

Аналогично следует поступать с матрицами 5×5, 6×6 и другими больших размерностей.

Преобразования матриц нужно выполнять в соответствии со свойствами определителя. Но прежде чем перейти к практике по вычислению определителя для матриц 4×4, давайте вернёмся к матрицам 3×3 и подробно рассмотрим, как вычисляется определитель для них.

Минор

Определитель матрицы не очень прост для понимания, поскольку в его понятии присутствует рекурсия: определитель матрицы состоит из нескольких элементов, в том числе из определителя (других) матриц.

Чтобы не застрять на этом, давайте прямо сейчас (временно) примем, что определитель матрицы

Ещё разберёмся в условных обозначения и в таких понятиях как минор и алгебраическое дополнение.

Буквой i мы обозначаем порядковый номер стоки, буквой j – порядковый номер столбца.

a_ij означает элемент матрицы (цифру) на пересечении строки i и столбца j.

Представим себе матрицу, которая получена из исходной удалением строки i и столбца j. Определитель новой матрицы, которая получена из исходной удалением строки i и столбца j, называется минором M_ij элемента a_ij.

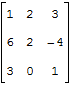
Проиллюстрируем сказанное. Предположим, дана матрица

Тогда для определения минора M₁₁ элемента a₁₁ нам нужно составить новую матрицу, которая получается из исходной удалением первой строки и первого столбца:

И вычислить для неё определитель: 2*1 — (-4)*0 = 2

Для определения минора M₂₂ элемента a₂₂ нам нужно составить новую матрицу, которая получается из исходной удалением второй строки и второго столбца:

Алгебраическое дополнение

Алгебраическим дополнением А_ij для элемента a_ij называется минор M_ij этого элемента, взятый со знаком «+», если сумма индексов строки и столбца (i + j), на пересечении которых стоит этот элемент, чётная, и со знаком «-», если сумма индексов нечётная.

Для матрицы из предыдущего примера

Вычисление определителя для матриц

Определителем порядка n, соответствующим матрице А, называется число, обозначаемое det A и вычисляемое по формуле:

В этой формуле нам всё уже знакомо, давайте теперь посчитаем определитель матрицы для

Каков бы ни был номер строки i=1,2,…, n или столбца j = 1, 2,…, n определитель n-го порядка равен сумме произведений элементов этой строки или этого столбца на их алгебраические дополнения, т. е.

Т.е. детерминант можно вычислить по любому столбцу или по любой строке.

Чтобы убедиться в этом, вычислим определитель для матрицы из последнего примера по второму столбцу

Свойства определителя матриц

Для вычисления определителя любого порядка можно применять метод последовательного понижения порядка определителя. Для этого пользуются правилом разложения определителя по элементам строки или столбца. Еще один способ вычисления определителей заключается в том, чтобы с помощью элементарных преобразований со строками (или столбцами), прежде всего в соответствии со свойствами 4 и 7 определителей, привести определитель к виду, когда под главной диагональю определителя (определяемой так же, как и для квадратных матриц) все элементы равны нулю. Тогда определитель равен произведению элементов, расположенных на главной диагонали.

При вычислении определителя последовательным понижением порядка для уменьшения объема вычислительной работы целесообразно с помощью свойства 7 определителей добиться обнуления части элементов какой-либо строки или какого-либо столбца определителя, что уменьшит число вычисляемых алгебраических дополнений.

Приведение матрицы к треугольному виду, преобразование матрицы, облегчающее вычисление определителя

Показанные ниже методы нецелесообразно использовать для матриц 3×3, но я предлагаю рассмотреть суть методов на простом примере. Воспользуемся матрицей, для которой мы уже считали определитель — нам будет проще проверить правильность вычислений:

Используя 7-е свойство определителя, вычтем из второй строки третью, умноженную на 2:

из третьей строки вычтем соответствующие элементы первой строки определителя, умноженные на 3:

Так как элементы определителя, расположенные под его главной диагональю, равны 0, то, следовательно, определитесь равен произведению элементов, расположенных на главной диагонали:

Как видим, ответ совпал с полученными ранее.

Давайте вспомним формулу определителя матрицы:

Детерминант — это сумма алгебраических дополнений, умноженная на члены одной из строк или одного из столбцов.

Если в результате преобразований мы сделаем так, что одна из строк (или столбец) будет состоять полностью из нулей кроме одной позиции, то нам не нужно будет считать все алгебраические дополнения, поскольку они заведомо будут равны нулю. Как и предыдущий метод, этот целесообразно применять для матриц больших размеров.

Покажем пример на той же самой матрице:

Вычислим определитель по второму столбцу. Нам нужно посчитать только одно алгебраическое дополнение, поскольку остальные заведомо сводятся к нулю:

Вычисление определителя для матриц 4×4, 5×5 и больших размерностей

Чтобы избежать слишком больших вычислений для матриц больших размеров следует делать преобразования, описанные выше. Приведём пару примеров.

Вычислить определитесь матрицы

Р е ш е н и е. Используя 7-е свойство определителя, вычтем из второй строки третью, из четвёртой строки — соответствующие элементы первой строки определителя, умноженные соответственно на 3, 4, 5. Эти действия сокращённо будем обозначать так: (2) — (1) * 3; (3) — (1) * 4; (4) — (1) * 5. Получим:

Далее, в соответствии с ведёнными обозначениями, выполним действия: (3) — (2) * 8; (4) — (2) * 9. Получаем

Так как элементы определителя, расположенные под его главной диагональю, равны 0, то, следовательно, определитесь равен произведению элементов, расположенных на главной диагонали:

Вычислить определитель

Разлагая полученный определитесь по второй строке имеем:

(Затем мы вынесли сомножитель 2 первого столбца на основании свойства 4). Далее прибавим к элементам первого и второго столбца элементы определителя. Получим:

Затем мы вынесли множитель в первом столбце, а затем общий множитель (-1) в первой строке. Разлагая теперь получившийся определитесь третьего порядка по элементам второй строки получим:

Здесь определитесь второго порядка вычислен в соответствии с его определением, по формуле

Вычисление определителя (детерминанта) матрицы wxMaxima и Maxima

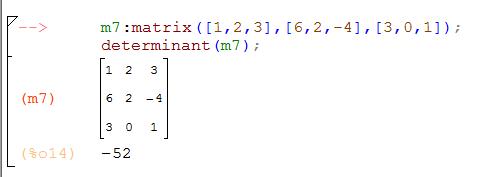
В wxMaxima и Maxima для вычисления определителя используется функция determinant:

Для приведения матриц к треугольному виду можно воспользоваться функцией triangularize:

Источник

Значение слова «детерминант»

детермина́нт

1. матем. определитель матрицы; скалярная величина, которая может быть вычислена и поставлена в однозначное соответствие матрице

2. книжн. определитель, определяющий фактор ◆ Так, например, один и тот же локальный, темпоральный, объектный детерминант может распространять двусоставное предложение, односоставное предложение именное, спрягаемо-глагольное, инфинитивное, наречное. Наталия Шведова, «Русский язык», 2017 г.

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова гиперболоид (существительное):

Синонимы к слову «детерминант&raquo

Предложения со словом «детерминант&raquo

Понятия, связанные со словом «детерминант»

В настоящее время отсутствует единое определение точно решаемой задачи для всех разделов математики. Это обусловлено особенностями самих задач и методов поиска их решения. Вместе с тем базовые теоремы, определяющие наличие и единственность решений, строятся на общих принципах, что будет показано ниже.

Отправить комментарий

Дополнительно

Предложения со словом «детерминант&raquo

Для нашего же времени подчинение как одна из детерминант поведения особенно актуально.

Это основная детерминанта всех жизненных проявлений личности.

Обычно в этих концепциях постулируется некая потребность как главная детерминанта развития.

Источник

Для чего нужен детерминант

det А

Итак, det А ,

Например, для n 2

,

для n 3

Правило вычисления определителя равносильно правилу треугольников (правилу Саррюса), которое схематически можно записать как

ОСНОВНЫЕ СВОЙСТВА ОПРЕДЕЛИТЕЛЯ

1. Равноправие строк и столбцов. При транспонировании матрицы ее определитель не меняется.

2. Если все элементы какого-либо столбца (строки) определителя равны нулю, то определитель также равен нулю. Это свойство очевидно, так как каждое слагаемое содержит по одному и только одному сомножителю из каждого столбца (строки).

3. Антисимметрия. При перестановке двух любых столбцов (строк) определителя его знак меняется на противоположный, а абсолютная величина остается неизменной.

Доказательство свойств 1 и 3 основано на правиле расстановки знаков членов определителя.

4. Определитель с двумя одинаковыми столбцами (строками) равен нулю.

Действительно, при перестановке, например, двух одинаковых столбцов определитель не изменяется, но вместе с тем он в силу третьего свойства меняет знак на обратный, т. е.

, откуда или .

6. Общий множитель всех элементов какого-либо столбца (строки) определителя можно вынести за его знак. Отсюда следует, что если какой-либо столбец (строку) определителя умножить на число λ, то сам определитель умножится на это число.

7. Если какой-либо столбец (строка) определителя является линейной комбинацией других его столбцов (строк), то определитель равен нулю.

Свойства 6 и 7 вытекают из пятого свойства.

8. Определитель не изменится, если к любому его столбцу (строке) прибавить произвольную линейную комбинацию его столбцов (строк).

Действительно, в силу линейности определитель равен сумме исходного определителя и определителя с двумя одинаковыми столбцами (строками).

Доказательство следует из свойства линейности определителя.

Источник

Методы вычисления определителей

I. Перестановка двух столбцов (строк) определителя приводит к изменению его знака на противоположный.

II. Умножение всех элементов одного столбца (строки) определителя на одно и то же число, отличное от нуля, приводит к умножению определителя на это число.

III. Прибавление к элементам одного столбца (строки) определителя соответствующих элементов другого столбца, умноженных на одно и то же число, не изменяет определитель.

При помощи элементарных преобразований можно упростить определитель, т.е. привести его к виду, удобному для вычислений.

Метод приведения определителя к треугольному виду

При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.

Итак, метод состоит из двух шагов.

1. При помощи элементарных преобразований привести определитель к треугольному виду.

2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.

Пример 2.12. Вычислить определитель четвёртого порядка

Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):

Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется.

В полученной матрице нужно сделать равными нулю элементы и второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:

Получили определитель треугольного вида.

2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали :

Метод понижения порядка определителя

Этот метод также основан на элементарных преобразованиях определителя.

1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.

2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.

Пример 2.13. Вычислить определитель четвёртого порядка методом понижения порядка.

2. Разложим определитель по второй строке

Получили определитель третьего порядка.

Прибавим ко второму столбцу первый

Полученный определитель разложим по второму столбцу

Получили определитель 2-го порядка.

Прибавим ко второй строке первую, умноженную на (-2)

Разложим определитель по второй строке и заменим определитель первого порядка единственным его элементом

Результат совпадает с полученным в примере 2.7.

Метод изменения всех элементов определителя

При вычислении определителей бывает полезно изменить все его элементы, умножив их на одно и то же число, не равное нулю, либо прибавить к каждому элементу одно и то же число. Найдем формулы изменения определителя при этих преобразованиях.

Применяя свойство 7 к первому столбцу этого определителя, получаем сумму определителей

отличающихся от определителя матрицы только j-м столбцом. Раскладывая этот определитель по j-му столбцу, получаем сумму алгебраических дополнений элементов этого столбца, умноженную на

Пример 2.14. Вычислить определитель n-го порядка

Решение. Рассмотрим определитель диагональной матрицы

Определитель диагональной матрицы равен произведению диагональных элементов:

Вычисление определителей с помощью рекуррентных уравнений

Этот метод заключается в том, что исходный определитель n-го порядка выражается через определители того же вида, но меньшего порядка. Получается рекуррентное уравнение

Решая это уравнение, находим формулу, выражающую определитель через определители и порядок

В последнюю формулу подставляем определители невысокого порядка, которые нетрудно вычислить каким-либо другим способом.

Пример 2.15. Вычислить определитель n-го порядка

Решение. Разложим определитель по первой строке

Следовательно, искомый определитель удовлетворяет рекуррентному уравнению

Подберем теперь коэффициенты и в формуле так, чтобы при и она давала правильные результаты, т.е.

Пример 2.16. Вычислить определитель Вандермонда

Решение. Рассмотрим определитель

где старший коэффициент равен алгебраическому дополнению элемента

Источник