Для чего нужен эпсилон
что какой эпсилон
Ε, ε (название: э́псилон, греч. έψιλον) — 5-я буква греческого алфавита. В системе греческой алфавитной записи чисел имеет числовое значение 5. Происходит от финикийской буквы hé — hé. От буквы «эпсилон» произошли латинская E и кириллическая Е. Название «эпсилон» (греч. Ε ψιλόν — «е простое» ) было введено для того, чтобы отличать эту букву от созвучного сочетания αι.
Использование
Заглавная буква эпсилон в основном не используется как символ, поскольку пишется так же, как и заглавная латинская буква E.
В различных дисциплинах при помощи строчной буквы ε обозначаются:
в математическом анализе — положительное сколь угодно малое вещественное число; см. примеры в статье Предел последовательности;
в алгебре — предельное порядковое число последовательности \omega,\omega^<\omega>,\omega^<\omega^<\omega>>,\dots.
в теории множеств — отношение принадлежности элемента множеству (такое обозначение является устаревшим, сейчас для той же цели используется символ ∈);
в тензорном исчислении — символ Леви-Чивиты;
в теории автоматов — эпсилон-переход;
в физике — угловое ускорение; коэффициент экстинкции оптического поглощения; проводимость среды; электронный захват; относительное удлинение; диэлектрическая проницаемость среды; энергия активации; ЭДС; ε0 — универсальная электрическая постоянная.
в астрономии — пятая (как правило) по яркости звезда в созвездии;
в программировании — точность численного типа данных;
в информатике — пустая строка;
в фонетике — неогубленный гласный переднего ряда средне-нижнего подъёма.
в теории метаболического контроля — эластичность фермента
Кто такие эпсилон самцы
03 Jun 2019 в 20:53
03 Jun 2019 в 20:53 #1
Всем известно кто такие альфа, беты, гамы, омежки.
А вот кто такие эпсилон самцы и их роль в обществе мне непонятно. На кого можно спроекцировать это мне тоже не понятно.
В нете инфы особой нету, только какая то дичь про охотников.
Жду ответы эспертов
03 Jun 2019 в 20:55 #2
Это которые специализируются на своём поле
03 Jun 2019 в 20:55 #3
Всем известно кто такие альфа, беты, гамы, омежки.
А вот кто такие эпсилон самцы и их роль в обществе мне непонятно. На кого можно спроекцировать это мне тоже не понятно.
В нете инфы особой нету, только какая то дичь про охотников.
Жду ответы эспертов
03 Jun 2019 в 20:56 #4
Заглавная буква эпсилон не используется как символ, поскольку пишется так же, как и заглавная латинская буква E.
В различных дисциплинах при помощи строчной буквы ε обозначаются:
эпсилон
От Земли до Беты — восемь дён,
Сколько ж до планеты Эпсило́н,
Не считаем мы, чтоб не сойти с ума.
В. С. Высоцкий, Песня космических негодяев
Смотреть что такое «эпсилон» в других словарях:
эпсилон — сущ., кол во синонимов: 1 • буква (103) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
эпсилон — эпсилон, а (название буквы) … Русский орфографический словарь
эпсилон — Обозначение, обычно приписываемое интерметаллическим, металл металлоид и металл неметалл соединениям, встречающимся в системах железных сплавов, например: Fe3Mo2, FeSi и Fe3P. [http://sl3d.ru/o slovare.html] Тематики машиностроение в целом … Справочник технического переводчика
Эпсилон — У этого термина существуют и другие значения, см. E. Греческий алфавит Αα Альфа … Википедия
Эпсилон (ε) — Epsilon (ε) Эпсилон (ε). Обозначение, обычно приписываемое интерметаллическим, металл металлоид и металл неметалл соединениям, встречающимся в системах железных сплавов, например Fe3Mo2, FeSi и Fe3P. (Источник: «Металлы и сплавы. Справочник.» Под … Словарь металлургических терминов
Эпсилон — м. Название буквы греческого алфавита. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
эпсилон — (2 м); мн. э/псилоны, Р. э/псилонов … Орфографический словарь русского языка
Эпсилон-салон — Эпсилон салон самиздатский литературный альманах, выпускавшийся в 1985 1989 гг. в Москве Николаем Байтовым и Александром Барашом. Вышло 18 выпусков, каждый по 70 80 страниц, в машинописном исполнении, тиражом 9 экземпляров. По словам… … Википедия
Эпсилон (буква) — Греческий алфавит Α α альфа Β β бета … Википедия
Машинный эпсилон
Плавающая запятая — форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто используемое представление утверждено в стандарте IEEE 754. Реализация математических операций с числами с плавающей запятой в вычислительных системах может быть как аппаратная, так и программная.
Содержание
«Плавающая запятая» и «плавающая точка»
Так как в некоторых, преимущественно англоязычных и англофицированных, странах (см. подробный список Decimal separator (англ.) ) при записи чисел целая часть отделяется от дробной точкой, то в терминологии этих стран фигурирует название «плавающая точка» (floating point (англ.) ). Так как в России целая часть числа от дробной традиционно отделяется запятой, то для обозначения того же понятия используется термин «плавающая запятая».
Происхождение названия
Название «плавающая запятая» происходит от того, что запятая в позиционном представлении числа (десятичная запятая, или, для компьютеров, двоичная запятая — далее по тексту просто запятая) может быть помещена где угодно относительно цифр в строке. Это положение запятой указывается отдельно во внутреннем представлении. Таким образом, представление числа в форме с плавающей запятой может рассматриваться как компьютерная реализация экспоненциальной записи чисел.
Преимущество использования представления чисел в формате с плавающей запятой над представлением в формате с фиксированной запятой (и целыми числами) состоит в том, что можно использовать существенно больший диапазон значений при неизменной относительной точности. Например, в форме с фиксированной запятой число, занимающее 8 разрядов в целой части и 2 разряда после запятой, может быть представлено в виде 123456,78; 8765,43; 123,00 и так далее. В свою очередь, в формате с плавающей запятой (в тех же 8 разрядах) можно записать числа 1,2345678; 1234567,8; 0,000012345678; 12345678000000000 и так далее.
Скорость выполнения компьютером операций с числами, представленными в форме с плавающей запятой, измеряется в англ. FLOPS — число операций с плавающей запятой в секунду ),
Структура числа
Число с плавающей запятой состоит из:
Нормальная форма
Использование в вычислительных машинах
Краткий обзор
Существует несколько способов того, как строки из цифр могут представлять числа:
Запись числа в форме с плавающей запятой позволяет производить вычисления над широким диапазоном величин, сочетая фиксированное количество разрядов и точность. Например, в десятичной системе предоставления чисел с плавающей запятой (3 разряда) операцию умножения, которую мы бы записали как
в нормальной форме представляется в виде
(1,20 × 10 −1 ) × (1,20 × 10 −1 ) = (1,44 × 10 −2 ).
В формате с фиксированной запятой мы бы получили вынужденное округление
Мы потеряли крайний правый разряд числа, так как данный формат не позволяет запятой «плавать» по записи числа.
Диапазон чисел, представимых в формате с плавающей запятой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 52 бита + 1 знаковый, показатель — 11 бит. Таким образом получаем диапазон точности примерно от 4,94 × 10 −324 до 1.79 × 10 308 (от 2 −52 × 2 −1022 до
1 × 2 1024 ). Пара значений показателя зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся значения бесконечность), получающихся в результате операций типа деления на ноль нуля, положительных и отрицательных чисел. Также сюда попадают денормализованные числа, у которых мантисса меньше единицы. В специализированных устройствах (например GPU) поддержка специальных чисел часто отсутствует. Существуют программные пакеты, в которых объём памяти выделенный под мантиссу и показатель задаётся программно, и ограничивается лишь объёмом доступной памяти ЭВМ.
Машинный эпсилон
В отличие от фиксированной запятой, сетка чисел, которые способна отобразить арифметика с плавающей запятой, неравномерна: она более густая для чисел малого порядка и более редкая — для больших чисел. Но относительная погрешность записи чисел одинакова и для малых чисел, и для больших. Поэтому можно ввести понятие машинного эпсилона.
Машинным эпсилоном называется наименьшее положительное число ε такое, что 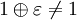

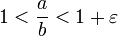
ЭПСИЛОН-РАЗЛОЖЕНИЕ
Уменьшение числа степеней свободы (в единице объёма) при описании критич. явлений проводится обычно посредством перехода от микроскопич. узельных, или «ячеечных», спинов к макроскопич. квазинепрерывным «блочным» спинам, определяемым как нек-рое среднее (разумеется, не в термодинамич. смысле) от b d дискретных ячеечных спинов. Здесь b>=1— целое число, указывающее, во сколько раз каждое из d рёбер гиперкубич. спинового «блока» превосходит постоянную исходной решётки. Описанная операция проводится столько раз, сколько необходимо, чтобы линейные размеры блока стали порядка x (очевидно, это вполне аналогично операции сглаживания или крупнозернистого усреднения, используемой, напр., в гидродинамике). С др. стороны, переход к блочным спинам, обладающим пространственным разрешением
С др. стороны, учитывая, что величина
описывает спиновую конфигурацию в масштабах вплоть до b
суммирование по i и j проводится от 1 до n, а модули всех волновых векторов под знаком суммы ограничены сверху величиной Л.

В окрестности m* действие преобразования РГ имеет вид
k 2 , а массовый оператор S(k) в низших порядках по взаимодействию может быть разложен по степеням ln k:. С др. стороны, согласно результатам анализа по методу РГ, вблизи критич. точки G(k)
от «несущественных», возникающих благодаря наличию несуществ. переменной t 2 . с малым показателем у 2 = О(e); для этого необходимо подобрать спец. вид ф-ции u(e) (обычно такой, чтобы обратить t 2 . в нуль). Очевидно, от выбора и(e), равно как и от величины и способа введения параметра обрезания L, согласно гипотезе универсальности, не должен зависеть окончательный результат; описанная процедура наз. исключением медленного переходного процесса или расширением критич. области (Вильсон, 1971).
Родственными Э.-р. в квантовой статистич. физике являются также разложения на малых расстояниях и на световом конусе для произведений локальных токов в КТП. Напр., произведения двух локальных токов J(x+l) и J(x—l) при малых пространственно-временных векторах l ведут себя след. образом:
Метод РГ для критич. явлений, в том числе Э.-р. до настоящего времени не имеет вполне надёжного матем. обоснования, а также к.-л. однозначной реализации. Существует ряд подходов, основанных на использовании теории возмущений, рекуррентных ф-л, дифференц. ур-ний и т. п., каждый из к-рых обладает своими преимуществами и недостатками. Однако в целом метод РГ наиб. предпочтителен для анализа критич. явлений, т. к. в отличие от прямых методов вычисления статистич. суммы и корреляц. ф-ций преобразования РГ действуют в пространстве несингулярных величин и предоставляют широкие возможности для построения аппроксимаций, в т. ч. прямых численных расчётов с использованием ЭВМ.
Лит.: Вильсон К., Когут Дж., Ренормализационная группа и e-разложение, пер. с англ., М., 1975; Ландау Л. Д., Лиф-шиц Е. М., Статистическая физика, ч. 1, 3 изд., М., 1976, p 147; Паташинский А. 3., Покровский В. Л., Флуктуационная теория фазовых переходов, 2 изд., М., 1982; Pfeuty P., Toulouse G., in: Introduction to the renormalization group and to the critical phenomena, L.- N. Y., 1977; Ma Ш,, Современная теория критических явлений, пер. с англ., М., 1980; Изюмов Ю. А., Скрябин Ю. Н., Статистическая механика магнитоупорядочен-ных систем, М., 1987. Ю. Г. Рудой.











