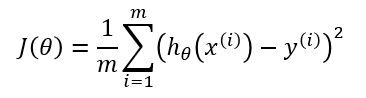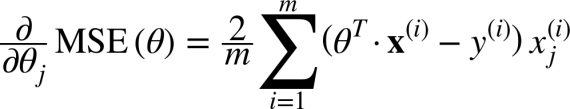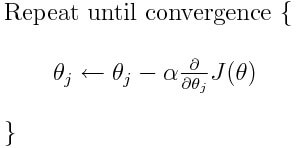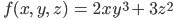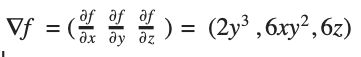Для чего нужен градиентный спуск
Градиентный спуск: всё, что нужно знать
Градиентный спуск — самый используемый алгоритм обучения, он применяется почти в каждой модели машинного обучения. Градиентный спуск — это, по сути, и есть то, как обучаются модели. Без ГС машинное обучение не было бы там, где сейчас. Метод градиентного спуска с некоторой модификацией широко используется для обучения персептрона и глубоких нейронных сетей, и известен как метод обратного распространения ошибки.
В этом посте вы найдете объяснение градиентного спуска с небольшим количеством математики. Краткое содержание:
Что такое градиентный спуск
Градиентный спуск — метод нахождения минимального значения функции потерь (существует множество видов этой функции). Минимизация любой функции означает поиск самой глубокой впадины в этой функции. Имейте в виду, что функция используется, чтобы контролировать ошибку в прогнозах модели машинного обучения. Поиск минимума означает получение наименьшей возможной ошибки или повышение точности модели. Мы увеличиваем точность, перебирая набор учебных данных при настройке параметров нашей модели (весов и смещений).
Итак, градиентный спуск нужен для минимизации функции потерь.
Суть алгоритма – процесс получения наименьшего значения ошибки. Аналогично это можно рассматривать как спуск во впадину в попытке найти золото на дне ущелья (самое низкое значение ошибки).
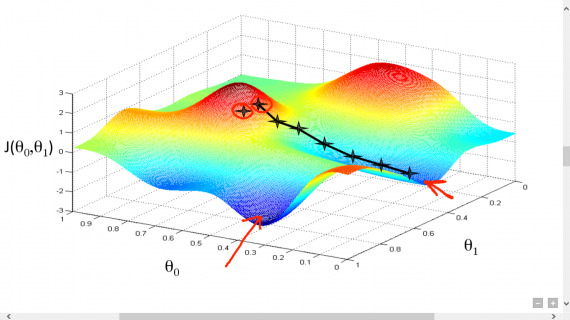
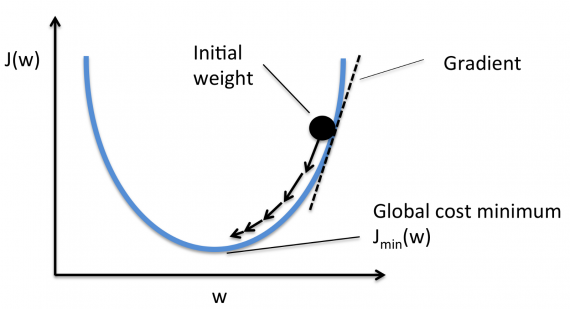
В дальнейшем, чтобы найти самую низкую ошибку (глубочайшую впадину) в функции потерь (по отношению к одному весу), нужно настроить параметры модели. Как мы их настраиваем? В этом поможет математический анализ. Благодаря анализу мы знаем, что наклон графика функции – производная от функции по переменной. Это наклон всегда указывает на ближайшую впадину!
На рисунке мы видим график функции потерь (названный «Ошибка» с символом «J») с одним весом. Теперь, если мы вычислим наклон (обозначим это dJ/dw) функции потерь относительно одного веса, то получим направление, в котором нужно двигаться, чтобы достичь локальных минимумов. Давайте пока представим, что наша модель имеет только один вес.
Важно: когда мы перебираем все учебные данные, мы продолжаем добавлять значения dJ/dw для каждого веса. Так как потери зависят от примера обучения, dJ/dw также продолжает меняться. Затем делим собранные значения на количество примеров обучения для получения среднего. Потом мы используем это среднее значение (каждого веса) для настройки каждого веса.
Также обратите внимание: Функция потерь предназначена для отслеживания ошибки с каждым примером обучениям, в то время как производная функции относительного одного веса – это то, куда нужно сместить вес, чтобы минимизировать ее для этого примера обучения. Вы можете создавать модели даже без применения функции потерь. Но вам придется использовать производную относительно каждого веса (dJ/dw).
Теперь, когда мы определили направление, в котором нужно подтолкнуть вес, нам нужно понять, как это сделать. Тут мы используем коэффициент скорости обучения, его называют гипер-параметром. Гипер-параметр – значение, требуемое вашей моделью, о котором мы действительно имеем очень смутное представление. Обычно эти значения могут быть изучены методом проб и ошибок. Здесь не так: одно подходит для всех гипер-параметров. Коэффициент скорости обучения можно рассматривать как «шаг в правильном направлении», где направление происходит от dJ/dw.
Это была функция потерь построенная на один вес. В реальной модели мы делаем всё перечисленное выше для всех весов, перебирая все примеры обучения. Даже в относительно небольшой модели машинного обучения у вас будет более чем 1 или 2 веса. Это затрудняет визуализацию, поскольку график будет обладать размерами, которые разум не может себе представить.
Подробнее о градиентах
Кроме функции потерь градиентный спуск также требует градиент, который является dJ/dw (производная функции потерь относительно одного веса, выполненная для всех весов). dJ/dw зависит от вашего выбора функции потерь. Наиболее распространена функция потерь среднеквадратичной ошибки.
Производная этой функции относительно любого веса (эта формула показывает вычисление градиента для линейной регрессии):
Это – вся математика в ГС. Глядя на это можно сказать, что по сути, ГС не содержит много математики. Единственная математика, которую он содержит в себе – умножение и деление, до которых мы доберемся. Это означает, что ваш выбор функции повлияет на вычисление градиента каждого веса.
Коэффициент скорости обучения
Всё, о чём написано выше, есть в учебнике. Вы можете открыть любую книгу о градиентном спуске, там будет написано то же самое. Формулы градиентов для каждой функции потерь можно найти в интернете, не зная как вывести их самостоятельно.
Однако проблема у большинства моделей возникает с коэффициентом скорости обучения. Давайте взглянем на обновленное выражение для каждого веса (j лежит в диапазоне от 0 до количества весов, а Theta-j это j-й вес в векторе весов, k лежит в диапазоне от 0 до количества смещений, где B-k — это k-е смещение в векторе смещений). Здесь alpha – коэффициент скорости обучения. Из этого можно сказать, что мы вычисляем dJ/dTheta-j ( градиент веса Theta-j), и затем шаг размера alpha в этом направлении. Следовательно, мы спускаемся по градиенту. Чтобы обновить смещение, замените Theta-j на B-k.
Если этот размера шага alpha слишком велик, мы преодолеем минимум: то есть промахнемся мимо минимума. Если alpha слишком мала, мы используем слишком много итераций, чтобы добраться до минимума. Итак, alpha должна быть подходящей.
Использование градиентного спуска
Что ж, вот и всё. Это всё, что нужно знать про градиентный спуск. Давайте подытожим всё в псевдокоде.
Примечание: Весы здесь представлены в векторах. В более крупных моделях они, наверное, будут матрицами.
От i = 0 до «количество примеров обучения»
1. Вычислите градиент функции потерь для i-го примера обучения по каждому весу и смещению. Теперь у вас есть вектор, который полон градиентами для каждого веса и переменной, содержащей градиент смещения.
2. Добавьте градиенты весов, вычисленные для отдельного аккумулятивного вектора, который после того, как вы выполнили итерацию по каждому учебному примеру, должен содержать сумму градиентов каждого веса за несколько итераций.
3. Подобно ситуации с весами, добавьте градиент смещения к аккумулятивной переменной.
Теперь, ПОСЛЕ перебирания всех примеров обучения, выполните следующие действия:
1. Поделите аккумулятивные переменные весов и смещения на количество примеров обучения. Это даст нам средние градиенты для всех весов и средний градиент для смещения. Будем называть их обновленными аккумуляторами (ОА).
2. Затем, используя приведенную ниже формулу, обновите все веса и смещение. Вместо dJ / dTheta-j вы будете подставлять ОА (обновленный аккумулятор) для весов и ОА для смещения. Проделайте то же самое для смещения.
Это была только одна итерация градиентного спуска.
Повторите этот процесс от начала до конца для некоторого количества итераций. Это означает, что для 1-й итерации ГС вы перебираете все примеры обучения, вычисляете градиенты, потом обновляете веса и смещения. Затем вы проделываете это для некоторого количества итераций ГС.
Различные типы градиентного спуска
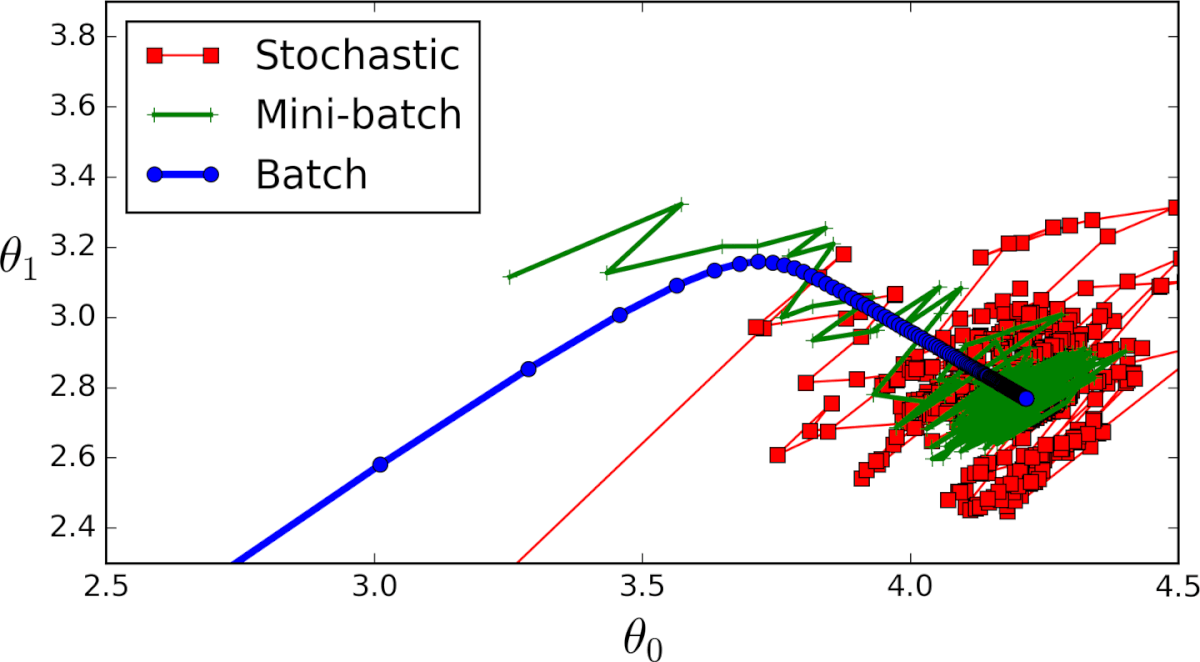
Существует 3 варианта градиентного спуска:
1. Мini-batch: тут вместо перебирания всех примеров обучения и с каждой итерацией, выполняющей вычисления только на одном примере обучения, мы обрабатываем n учебных примеров сразу. Этот выбор хорош для очень больших наборов данных.
2. Стохастический градиентный спуск: в этом случае вместо использования и зацикливания на каждом примере обучения, мы ПРОСТО ИСПОЛЬЗУЕМ ОДИН РАЗ. Есть несколько вещей замечаний:
3. Серия ГС: это то, о чем написано в предыдущих разделах. Цикл на каждом примере обучения.
Пример кода на python
Применимо к cерии ГС, так будет выглядеть блок учебного кода на Python.
Вот и всё. Теперь вы должны хорошо понимать, что такое метод градиентного спуска.
Понимание градиентного спуска
Дата публикации Aug 29, 2019
Минимизация ошибки между моделью и набором обучающих данных является фундаментальной практикой в науке о данных. В конце концов, если модель не соответствует обучающему набору данных, то она явно не будет иметь предсказательной силы.
Примеры этой концепции см.Понимание основ линейной регрессииа такжеПонимание множественной регрессии, В обоих случаях модель определенного типа (либо линейная регрессия, либо множественная регрессия) соответствовала набору данных путем минимизации ошибки.
Чтобы минимизировать ошибку в модели, также необходимо иметь возможность рассчитать ошибку. И сделать это таким образом, чтобы охватить сложность ситуации, оставаясь чувствительным к серьезным проблемам исследователя данных. Это требует хорошо написанной функции стоимости, как было описано вФункции стоимости: основы машинного обучения,
После того как тип модели выбран и написана функция стоимости, последняя часть реализует инструмент для минимизации функции стоимости, таким образом подгоняя модель к данным. Функция стоимости будет варьировать параметры модели по мере необходимости, чтобы найти наилучшее соответствие.
Градиентный спуск является мощным инструментом для этой роли.
Что такое градиентный спуск?
Давайте начнем объяснять градиентный спуск, продумывая пример. Представьте себе параболу. Параболы имеют как постоянно меняющиеся склоны, так и минимальную точку. Минимальная точка возникает там, где уклон равен нулю, поскольку это также точка, где уклон начинает увеличиваться с другой стороны.
Для тех, кто знаком с исчислением, это равносильно тому, что минимум происходит в точке, где производная уравнения равна нулю.
Теперь представьте, что мы начинаем с определенной точки и хотим достичь минимума. Нам не нужно указывать конкретный момент прямо сейчас, поскольку это все концептуально. Мы можем рассчитать наклон в любом направлении от нашей начальной точки, определить, какой наклон положительный, а какой отрицательный, и двигаться в направлении отрицательного наклона. Это автоматически приблизит нас к минимуму.
Постепенно и неоднократно движение в этом направлении в конечном итоге найдет минимальную точку.
Использование градиентного спуска для нахождения минимальной точки параболы немного глупо; это простой инструмент для этого простого примера. Но что происходит, когда есть много переменных, со многими различными уклонами в разных направлениях? Вот где сила автоматизации процесса становится очевидной.
Как работает градиентный спуск?
Градиентный спуск автоматически выполняет все шаги, описанные в нашем предыдущем примере с параболой. Конкретно это:
Это вызывает вопрос о размере шага. Как алгоритм градиентного спуска выбирает размер шага?
Как выбрать размер шага?
Действительно, это может быть сложным выбором. Это обычно называют скорее искусством, чем наукой.
Маленькие шаги с наименьшей вероятностью могут перескочить и пропустить минимальную точку. Это хорошо. Маленькие шаги самые точные. С другой стороны, они могут привести к невероятно длительным поискам.
Представьте себе, что вы работаете с градиентным спуском и хотите быть настолько уверенным, что вы точно нашли минимум, что вы используете минимальный размер шага, а алгоритм должен повторяться миллиард раз. Это не хорошо.
Но в то же время вы хотите, чтобы размер шага был достаточно маленьким, чтобы не допустить перерегулирования.
Некоторые возможные решения этой проблемы включают в себя:
К сожалению, ни один из этих подходов не является явным победителем.
Постепенное уменьшение размера шага не работает должным образом, потому что уменьшение размера шага может происходить либо слишком медленно, либо слишком быстро. Быстрое уменьшение размера шага приводит к проблеме, которую этот алгоритм пытался избежать, крошечному размеру шага и множеству итераций. Медленное уменьшение размера шага может привести к другой проблеме превышения минимальной точки.
Расчет оптимального размера шага работает фантастически, но очень затратно для вычислений. Это действительно уменьшает количество итераций, но каждая итерация занимает так много времени, что существенно не сокращает время вычислений.
Одним из отличных решений является использование псевдо-версии расчета оптимального размера шага. Это можно сделать, предоставив алгоритму массив возможных размеров шагов. Затем алгоритм перебирает все возможные размеры шагов, находит наилучший результат и выполняет этот шаг. Это более точно, чем автоматическое изменение размера шага с течением времени, и более эффективное по времени вычисление оптимального размера шага в каждой точке.
Он обеспечивает гибкое решение, которое работает достаточно хорошо в каждой точке, не слишком дорого в вычислительном отношении.
Каковы ограничения градиентного спуска?
Наиболее распространенным решением этой проблемы является стохастический градиентный спуск.
Что такое стохастический градиентный спуск?
Стохастический градиентный спуск основан на предположении, что ошибки в каждой точке в пространстве параметров являются аддитивными. Ошибка в точке один может быть добавлена к ошибке в точке два, которая может быть добавлена к ошибке в точке три, и так далее для всех точек.
Это означает, что модели не нужно рассчитывать ошибку во всех точках одновременно (вычислительно дорогой процесс). Вместо этого он может рассчитать ошибку в каждой точке отдельно и суммировать их вместе.
Кстати, это предположение почти всегда верно. Лучше на минуту подумать, чтобы убедиться, что это правда в вашей проблеме, а не просто предположить, что это так, но вы обнаружите, что это правда в подавляющем большинстве случаев.
Используя это предположение, стохастический градиентный спуск может рассчитать ошибку в каждой точке последовательно. Это экономит огромное количество времени на вычисления.
Это резко увеличивает скорость каждого шага в процессе градиентного спуска. Стохастический градиентный спуск все еще является итеративным процессом, определяющим направление и движущимся к минимальному шагу за раз.
Недостатком стохастического градиентного спуска является то, что он не находит истинный минимум так надежно. Вместо этого он имеет тенденцию быть очень близко, а затем обвести минимум навсегда. Чтобы избежать этого, важно установить порог улучшения. Если повторяющиеся итерации через функцию градиентного спуска не приведут к значительному сокращениюфункция стоимоститогда вы просто кружите вокруг минимальной точки. Пришло время выйти из процесса градиентного спуска и принять доступные результаты.
Объединяя все вместе
Градиентный спуск является важным инструментом в создании прогнозных моделей для науки о данных. Это общий подход к оптимизации, используемый для минимизациифункция стоимости, тем самым находя оптимальные параметры в ваших моделях. Например, он обычно используется длялинейная регрессияилимножественная регрессиямодели к тренировочному набору данных.
Этот алгоритм работает путем вычисления наклона кривой в каждом направлении в ее точке в пространстве данных и настройки параметров для перемещения в направлении наиболее отрицательного наклона. Для тех, кто знаком с исчислением, он делает это с частными производными.
Определение размера шага является фундаментальной проблемой использования градиентного спуска. Небольшие размеры шагов гарантируют нахождение истинного минимума, но также дают много итераций и длительное время вычислений. Большие размеры шагов выполняются быстрее, но с большей вероятностью выходят за рамки минимальной точки. Распространенным решением является предоставление модели нескольких различных размеров шага на выбор. Затем он рассчитывает улучшение с каждым размером шага и перемещается так далеко Это повышает точность за исключением использования большого размера шага, одновременно избегая проблем со временем вычисления маленьких шагов.
Оптимизация наборов параметров с использованием градиентного спуска может занять очень много времени. Это связано с тем, что он должен вычислять ошибку для всего набора данных одновременно. Стохастический градиентный спуск позволяет избежать этой проблемы, предполагая, что ошибки являются аддитивными. Таким образом, он может вычислять ошибку в каждой точке последовательно, уменьшая вычислительные требования к компьютеру. Это дает значительно более быстрые результаты.
[1] Для тех, кто не изучал исчисление, частные производные являются наклоном уравнения одной переменной. Например, частная производная по B для A = 0,25 + 0,9 * B + B * C + 1,2 C равна 0,9 + C.
[2] «Наиболее отрицательный наклон» относится к тому факту, что, вероятно, будет много направлений с отрицательным наклоном. Чтобы найти минимум как можно быстрее, градиентный спуск использует направление с наибольшим абсолютным значением отрицательного наклона.
[3] Как далеко это шаг? Как узнать размер шага? Хорошие вопросы Продолжайте читать, они будут рассмотрены в ближайшее время.
Разбираем нейросети по частям: как работает градиентный спуск
Градиентный спуск — это способ поиска точек минимума или максимума в сложных функциях. Рассказываем, почему это так важно для обучения нейросетей
Нейросети сейчас везде, и даже цифровому гуманитарию от них не скрыться. Word2vec при помощи нейросети кодирует смысл слов (вот тут мы объясняли, как), а новые модели ELMO и BERT даже научились учитывать, что слова появляются в разных контекстах и от этого из смысл тоже может меняться. Этот текст — про то, что значит «обучить» нейросеть и кто «подбирает веса» отдельных нейронов.
А что вообще творится в нейросетях? Напомните!
Ранее мы рассказывали, как «сырые» данные (картинка, видео или текст) разбиваются на мелкие кусочки и подаются на каждый входной нейрон. Дальше входные нейроны анализируют что-то очень простое — есть ли в их кусочке картинки 10 белых пикселей, есть ли буква «Т» в слове — и если да, нейрон «активируется», то есть передает свой сигнал в следующий слой с определенной силой. Сигналы комбинируются, потом собираются в абстрактные комбинации десятков комбинаций сигналов, и в конце концов активируют один из нейронов, который классифицирует картинку как котика или хлеб.
А как активируется нейрон?
Нейрон — это функция, которая получает на вход числа (обычно много), что-то с ними делает и возвращает одно число (обычно от 0 до 1). Функция, из которой нейрон состоит, называется функцией активации, или передаточной функцией. Именно она отвечает за то, будет ли передан сигнал нейрона дальше (1 на выходе функции — если будет, 0 — если нет). В самом простом виде функция активации может быть пороговой:
В данном случае, если какие-то значения на входе нейрона дали положительную сумму — нейрон активировался. Порог активации здесь выглядит как вертикальная палочка, простой переключатель вкл/выкл, а значит, нейрон может быть либо активен, либо нет — как лампочка. Есть и более сложные функции, которые могут изменять силу выходного сигнала, могут «чуть-чуть активировать» нейрон, или «активировать его посильнее»:
Выбор функции активации нейронов влияет на то, какие задачи они могут решать, и их подбор — задача создателя нейросети. Если создатель понимает, какие функции для чего подходят, у него больше шансов сделать крутую нейросеть, которая решит его проблему.
Вот главное: нейрон — это функция. Чем больше ее значение, тем важнее сигнал нейрона для всей сети.
Почему это важно в контексте обучения нейросети?
Коротко: нейроны постоянно дают слишком сильный или слабый сигнал и сбивают предсказание, их нужно настраивать.
Нейроны глупые! Без ручной настройки силы их выходных сигналов нейросеть даёт случайные предсказания. К выходному значению нейрона можно (и нужно) прибавлять некоторый вес. Вес прибавляется или отнимается в зависимости от того, насколько сильно в прошлый раз нейросеть ошиблась с предсказанием. Этот этап работы, когда нейроны штрафуются за все прошлые «косяки», называется обратным распространением ошибки. Какие-то нейроны активируются слишком сильно, какие-то — слабо, но все равно они уводят предсказание нейросети в сторону от правильного. Поскольку нейронов слишком много, и за какие конкретно признаки каждый из них отвечает — неясно, настроить каждый вес вручную невозможно. Люди придумали способ настраивать веса автоматически.
Для этого существует функция потерь. Что она делает?
Коротко: ее значение возрастает, если нейросеть сильно ошибается. Значит, надо найти такое решение, где функция возрастать не будет.
Есть функция, возрастающая при сильной ошибке предсказания. Чем больше ошибка, тем сильнее уменьшаются (штрафуются) веса активированных нейронов. Человеку нужно свести меру ошибки к минимуму, научить нейросеть делать верные предсказания о том, котик на картинке или булочка. Если функция потерь дает высокие значения при большой ошибке, мы просто ищем такие веса, при которых она дает минимальные значения.
Кстати, функций потерь тоже существует много, они по-разному подходят для разных задач, и крутые программисты за 300к/сек знают, как в них сориентироваться. Функции потерь объединяет то, что они возрастают вместе с мерой ошибки предсказания. Она вычисляется просто: из числа X (предсказанного) вычитаем число Y (то, что должно было предсказаться) — получаем число Err. Оно становится одним из аргументов функции потерь.
Здесь надо вспомнить производные
Задача подбора весов нейронной сети также называется тренировкой или задачей оптимизации. (Ведь optimus — наилучший, а значит, мы и ищем лучшие веса?) Веса нам нужны те, при которых функция потерь принимает минимальное значение. Когда мы знаем это значение, рассчитать нужные веса становится легко — все равно, что решить уравнение.
А значит, желаемая схема обучения нейросети выглядит примерно так:
Функция потерь принимает минимальное значение → находим соответствующие этому значению веса → ошибка минимальна → предсказание нейросети точно → вы великолепны.
Только сначала нужно найти минимальное значение функции.
Как это делали в школе?
Когда на уроке алгебры учительница давала какой-нибудь многочлен и просила найти его минимум, мы поступали следующим образом:
Напомним, что производная функции выражает скорость ее возрастания или убывания. Её геометрический смысл — показать угол, под которым в данной точке проходит касательная к функции. Если производную (а значит, угол касательной) приравнять к нулю, то мы найдем точки, в которых касательная параллельна оси абсцисс.
Вот что это будут за точки: в них функция меняет направление. Такие точки обязательно становятся (хотя бы локальными) минимумами или максимумами функции. А вот как будут выглядеть касательные к этим точкам:
После этого (страшного или приятного?) математического флешбэка пора признаваться, что как раз вот так в нейронных сетях найти минимум функции потерь невозможно. У нее слишком много входных аргументов, и аналитические подходы (как показанный выше) не работают. Приходится применять специальный поисковой, пошаговый метод градиентного спуска (умное слово для него — «эвристический», то есть все тот же «поисковой», но еще умнее — по-гречески).
Вот главное: нам до сих пор нужно найти минимальное значение функции потерь, это минимизирует ошибку в предсказании нейросети. Но мы сейчас выяснили, что по-школьному это сделать не получится.
We need to go deeper
Если есть функция, зависящая от нескольких переменных, можно говорить о частной производной, то есть о такой производной, когда все остальные переменные, кроме той, которая нам интересна, становятся константами (то есть постоянными).
Поэтому вот вам таблица, попробуйте сказать, чему равна частная производная от переменной x функции
Помните, что если рассчитывать производную от x, то z становится константой и с ней ничего делать не нужно.
(Ответ будет чуть ниже, не подглядывайте!)
Математически фразу «производная функции y от переменной x» можно записать так:
Ответ к задаче: частная производная равна
Чему же равна частная производная в точке (x=3, z=4)? Теперь мы можем просто подставить значения 3 и 4 в полученное уравнение частной производной
Мы получим, что производная равна 23 + 44 = 22.
Пора рассказать, что такое градиент
Если для функции многих переменных по очереди рассчитать частные производные для каждой из переменных (и записать эти производные в ряд, и взять в скобочки), получится вектор, называемый градиентом. Так как одна переменная соответствует одной координатной оси, каждый элемент вектора показывает скорость изменения функции вдоль своей оси, а все вместе они показывают направление, в котором быстрее всего возрастает функция в целом.
Вот главное: градиент — это вектор, показывающий направление, в котором функция многих переменных быстрее всего возрастает или падает. «Градиент функции f» записывается так: ∇f (можно читать как «набла f»).
Вот небольшое упражнение. Попробуйте найти градиент функции
для переменных x, y, z?
Подсказка: должен получиться вектор с тремя элементами.
Сложность в том, чтобы уследить, какие из «констант» — множители переменной, что рассматриваются в данный момент, а какие — отбрасываются как слагаемые.
Объясните наконец, что такое градиентный спуск!
Градиентный спуск — это эвристический алгоритм, который выбирает случайную точку, рассчитывает направление скорейшего убывания функции (пользуясь градиентом функции в данной точке), а затем пошагово рассчитывает новые значения функции, двигаясь в выбранную сторону. Если убывание значения функции становится слишком медленным, алгоритм останавливается и говорит, что нашел минимум.
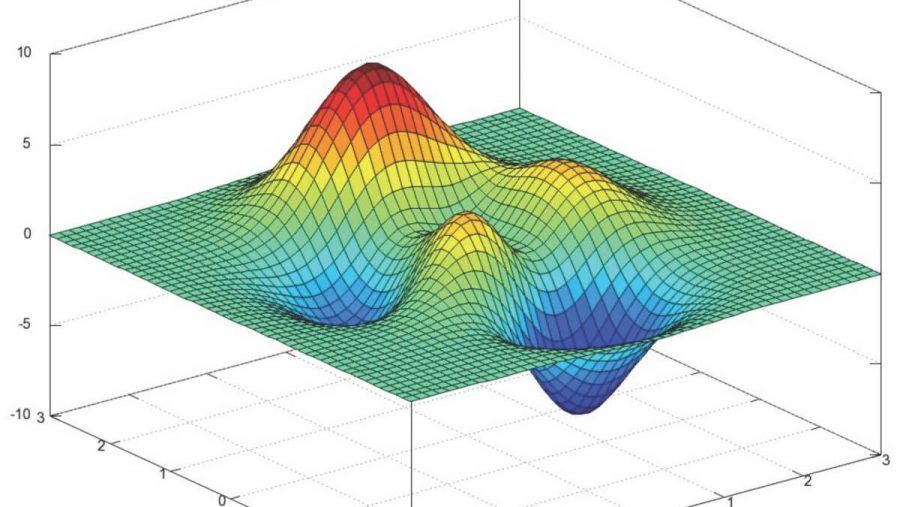
Стоит помнить, что говорим не о двумерных функциях. Представить, что происходит, можно по этой картинке:
Градиентный спуск выбирает случайную точку, находит направление самого быстрого убывания функции и двигается до ближайшего минимума вдоль этого направления. Кстати, размер одного шага можно настроить, это бывает очень важно. Если на каком-то этапе разность между старой точкой (до шага) и новой снижается ниже предела, считается, что минимум найден, алгоритм завершен. Можно вообразить работу градиентного спуска как игру в «холодно-горячо» до тех пор, пока степень «потепления» не станет пренебрежительно малой.
Вот главное: