Для чего нужен механизм
Механизмы
»Механизм — это совокупность тел (обычно — деталей машин), ограничивающих свободу движения друг друга взаимным сопротивлением. Механизмы служат для передачи и преобразования движения.
Как преобразователь движения механизм видоизменяет скорости, или траектории, или же и то, и другое. Он преобразует скорости, если при известной скорости одной из его частей другая его часть совершает движение, подобное движению первой, но с другой скоростью. Механизм преобразует траекторию, если, в то время как одна из его точек описывает известную траекторию, другая описывает другую заданную траекторию. Определенность движения механизма достигается попарным соединением его частей. Если требуется поставить тело A в такие условия, чтобы оно могло проходить последовательно только через определенные положения, то определяют поверхность, касательную ко всем этим положениям тела A (такая поверхность называется огибающей) и делают в неподвижном теле B канал, имеющий форму найденной огибающей. Тело A, помещенное в такой канал, будет способно только к определенному движению.
Содержание
Элементы механизмов
Такая совокупность двух тел, в которой формой одного тела определяется весь ряд последовательных положений, которые способно в нём занять другое тело, называется кинематической парой. Тела, составляющие пару, называются её звеньями. Например, тело, имеющее призматический канал, и помещенная в этом канале призма составляют поступательную пару, потому что одно из этих тел может совершать относительно другого только поступательное движение. Цилиндрическая втулка и помещенный в ней шип, снабженный закраинами, не дающими ему выскочить из втулки, составляют вращательную пару. Винт и гайка составляют винтовую пару. Расстояние между нарезками винта, считаемое по направлению оси винта, называется его шагом, так что, обойдя винт один раз, нарезка приближается к концу винта на один шаг. Поступательная пара может быть математически рассматриваема как такая винтовая, шаг которой равен бесконечности. Вращательная пара может быть рассматриваема как винтовая, шаг которой равен нулю. Эти пары называются простыми; отличительное свойство их заключается в том, что в них относительное движение одного звена по отношению к другому тождественно с относительным движением второго звена по отношению к первому.
Пары, не обладающие этим свойством, называются высшими. Таковы: зацепляющиеся между собой зубчатые колеса, шкив и перекинутый через него ремень, дуговой двухсторонник и полая трёхгранная призма и многие другие.
Движение звена A в звене B называется обращенным по отношению к движению звена B в звене A. Одну из наиболее интересных высших пар представляет собой эллиптический циркуль. Он состоит из доски, в которой сделаны два крестообразно пересекающихся между собой прямолинейных, перпендикулярных друг к другу прореза, и из стержня с выступающими на концах цилиндрическими шипами, диаметры которых равны ширине прорезов. Стержень вставляется шипами в прорезы так, чтобы один шип ходил по одному, а другой по другому из прорезов; с противоположной стороны на шипы навинчиваются винты с головками, препятствующими шипам выскочить из прорезов. При неподвижности доски траектория всех точек стержня суть эллипсы; как частные случаи эллипсов траектория центров шипов суть прямые линии, а траектория середины стержня — окружность. Движение стержня относительно доски происходит так, как будто бы соединённый с ним круг, построенный на нём как на диаметре, катился по внутренней стороне окружности, описанной из точки пересечения средних линий прорезов радиусом, равным диаметру катящегося круга. В обращенном движении, то есть при неподвижности стержня, все точки доски описывают улитки Паскаля (см. Кривые).
Звено B, соединённое в какую-либо пару со звеном A, может быть соединено в пару же со звеном C, которое, в свою очередь, может составлять пару со звеном D и так далее. Такое последовательное соединение звеньев в пары называется кинематической цепью. Если последнее звено кинематической цепи соединено в пару с первым, то цепь называется замкнутой, в противном случае она называется открытой. Такая кинематическая замкнутая цепь, которая при неподвижности одного из звеньев получает определенность движения, характеризующую механизм, называется принудительной. Когда в принудительной цепи одно из звеньев предполагается неподвижным, то говорят, что цепь поставлена на этом звене. Ставя принудительную цепь последовательно на разные её звенья, получим столько механизмов, сколько имеется звеньев в цепи. Примером принудительной цепи может служить шарнирный четырёхсторонник, состоящий из четырёх стержней, соединённых между собой вращательными парами, называемыми шарнирами.
Типы механизмов
Механизм, все точки которого описывают траектории, лежащие в параллельных между собой плоскостях, называется плоским. Движение твердого тела, в котором все точки его описывают траектории, параллельные одной и той же плоскости, называется также плоским. Всякое плоское движение происходит так, как будто бы некоторая кривая, соединённая неизменяемо с движущимся телом, катилась по некоторой другой неподвижной кривой. Эти кривые называются полодиями. Полодии, как катящиеся друг по другу кривые, постоянно прикасаются одна к другой. Их общая точка прикосновения называется мгновенным полюсом. В течение весьма малого промежутка времени движение тела можно рассматривать как бесконечно малое вращение около мгновенного полюса. Так, например, в описанном выше эллиптическом циркуле движение, как мы видели, приводится к катанию одного круга по другому; эти круги и есть суть полодии данного движения. Если бы весь эллиптический циркуль (и доска, и стержень) был подвижен, то все-таки относительное движение стержня и доски было бы то же самое и определялось бы катанием тех же полодий. Относительное движение каждых двух звеньев принудительной цепи, хотя бы эти звенья и не были соседними, составляя пару, характеризуется катанием двух соответствующих полодий (в плоском механизме). Всякое движение твердого тела (не плоское) приводится к катанию друг по другу, соединённому со скольжением, двух линейчатых поверхностей, называемых аксоидами.
Наибольшим практическим значением из всех высших пар пользуются зубчатые колеса, представляющие собой необходимое для преодоления более или менее значительных сопротивлений видоизменение катков. Цилиндрическими катками называются цилиндрические твердые тела, вращающиеся около своих геометрических осей и прикасающиеся друг к другу своими боковыми поверхностями, которые делаются шероховатыми. Если вращать один из таких катков, то благодаря существующему между катками трению и другой будет вращаться. Скорости вращения были бы обратно пропорциональны радиусам, если бы катки не скользили один по другому. Полодиями относительного движения двух соприкасающихся катков служат окружности основания самих катков. Чтобы устранить скольжение полодий, можно было бы на каждом из катков сделать впадины и выступы, чтобы выступы одного входили во впадины другого. Это и будут зубчатые колеса.
Полодии двух зацепляющихся между собой зубчатых цилиндрических (лобовых) колес суть окружности, называемые начальными. Отношение угловых (вращательных) скоростей обратно пропорционально радиусам начальных окружностей. Впадины и выступы зубчатого колеса образуют зубцы. Расстояние между двумя соответственными точками пересечения профилей двух соседних зубцов с начальной окружностью, считаемое по этой окружности, называется шагом. Приготовление зубчатого колеса начинается с того, что начальную окружность его, размер которой определяется по данной относительной скорости колеса, делят на столько равных частей, сколько зубцов предполагается сделать на колесе; расстояние между соседними точками деления и будет равно шагу. Шаги сцепляющихся колес должны быть равны между собой, а, следовательно, радиусы начальных окружностей пропорциональны числам зубцов. Если полодии относительного движения двух зубчатых колёс суть окружности, то отношение скоростей обратно пропорционально радиусам полодий и, следовательно, постоянно; такое постоянство и требуется от правильно устроенных колёс, а так как в зубчатых колесах полодии ничем не отмечены, то самая форма зубцов должна быть такова, чтобы при сцеплении их относительное движение колёс характеризовалось бы круговыми полодиями данных радиусов.
Существует несколько способов определения правильной формы зубцов, удовлетворяющих этому условию. Все эти способы основаны на следующем соображении. Пусть дан профиль зубца колеса A; покатим начальную окружность колеса A по начальной окружности колеса B на один шаг и найдем огибающую ко всем положениям, принимаемым при этом данным зубцом; эта огибающая и будет, по общему методу построения пар, представлять собой искомую форму зубца колеса B. Способ этот приложим к определению вида зубца колеса B в том случае, когда профиль зубца колеса A есть маленькая окружность, описанная из точки деления начальной окружности радиусом, раза в четыре меньшим шага; такое колесо называется цевочным и имеет зубцы, называемые цевками, в виде палок, параллельных оси колеса; профили цевок суть кружки, представляющие собой сечения цевок плоскостью, перпендикулярной к оси колеса. Покатим цевочное колесо A по колесу B; при этом центр цевки опишет эпициклоиду и огибающая последовательных положений цевки будет кривая, параллельная этой эпициклоиде и отстоящая от неё на расстояние радиуса цевки. Этой кривой и нужно ограничить бок зубца колеса B. Полный зубец ограничивается двумя такими боками, расположенными симметрично относительно средней линии зубца, направленной по радиусу колеса. а) Способ рулетт. Рулеттой называется кривая, чертимая какой-нибудь точкой кривой A, катящейся по кривой B. Пусть начальные окружности M и N колес соприкасаются взаимно в точке O. Построим произвольных радиусов вспомогательные круги P и Q, из которых P имел бы внутреннее прикосновение в точке O с M, круг же Q имел бы внутреннее прикосновение тоже в точке O с N. Покатим все четыре круга один по другому так, чтобы они постоянно соприкасались бы в одной точке. Изберем на P какую-нибудь точку a. Эта точка при катании P по M опишет гипоциклоиду p и при катании P по N опишет эпициклоиду q. Кривые p и q будут в течение движения соприкасаться взаимно потому, что обе чертятся одной и той же точкой a. Если принять p за форму впадины зубца колеса M, то q будет огибающая различных положений p и, как таковая, может быть принята за профиль выступа колеса N. Выступ колеса M и впадина колеса N образуются катанием кривой Q подобным же образом. Если взять радиус вспомогательной окружности P вдвое меньшим, то (как это видно из приведенной выше теории эллиптического циркуля) гипоциклоида p получает вид прямой. б) Способ развертывающих. Пусть O есть точка соприкосновения начальных окружностей; проведем через неё прямую, наклоненную к линии центров CC’ под углом 75°, опустим из центров C и C’ перпендикуляры CA и C’B на эту прямую и опишем из C и C’ окружности радиусами CA и C’B; вообразим себе твердые цилиндры, построенные на найденных вспомогательных окружностях, как на основаниях; обернем около цилиндра CA нитку, свободный конец которой вытянем до O, и в этом месте укрепим на нитку карандаш. Двигая карандашом направо и налево так, чтобы идущая с цилиндра нить оставалась натянутой, не скользила бы по цилиндру, а только развертывалась бы несколько с него при движении карандаша в одну сторону и навертывалась бы при движении карандаша в другую сторону, начертим кривую, называемую развертывающей (см. Кривые, табл. II, фиг. 11). Эта кривая и будет профилем зубца колеса C. Профиль зубца колеса C’ получается развертыванием нити с окружности C’B. в) Кроме этих точных способов построения зубцов, существуют ещё приближенные, состоящие в нахождении круговых дуг, близко подходящих к теоретически правильным кривым. Из таких способов наиболее известны изобретенные Виллисом, Чебышевым и Петровым. Длина зубцов определяется из условия, чтобы постоянно находились в зацеплении три зубца.
Для того, чтобы, не увеличивая длины зубцов, дать возможность большему их числу находиться в одновременном зацеплении, поступают следующим образом: на готовое зубчатое колесо кладут, так чтобы оси их совпадали, другое такое же колесо и поворачивают его на 1 /5 шага, на это колесо кладут третье и поворачивают его на 1 /5 шага относительно второго и так далее накладывают одно на другое пять колес, которые и скрепляют между собой наглухо в таком положении или, ещё лучше, отливают целиком штуку, имеющую форму таких сложенных колес; то же делают и для того колеса, которое должно сцепляться с приготовленным таким образом колесом. Такие колеса называются ступенчатыми, так как боковые поверхности их оказываются покрытыми ступенчатыми линиями. Если бы для приготовления ступенчатого колеса мы взяли не 5 толстых колёс, отступающих друг от друга на 1 /5 шага, а бесконечное множество бесконечно тонких колес, отступающих друг от друга на бесконечно малую часть шага, то на боковой поверхности получили бы не ступенчатые, а винтовые линии. Такие колеса с винтообразно идущими зубцами и отливаются (конечно целиком, а не из бесконечного числа тонких колёс, рассматриваемых только в теории). Эти колеса, по имени изобретателя называемые колесами Гука, употребляются в М., требующих большой плавности движения.
Если имеется ряд валов с насаженными на них наглухо последовательно зацепляющимися зубчатыми колесами, по одному колесу на каждом валу, то абсолютная величина отношения угловой скорости первого и последнего вала, сколько бы ни было промежуточных колес, будет та же самая, как если бы первое и последнее колесо зацеплялись между собой непосредственно. Если же желают изменить это отношение, как это требуется, например, при устройстве часов, то на 1-й вал насаживают колесо, сцепляющееся с маленьким колесом, называемым шестерней, насаженным на втором валу, на котором параллельно с шестерней насаживается колесо, сцепляющееся с шестерней 3-го вала, и так далее; наконец, колесо предпоследнего вала сцепляют с шестерней последнего вала. В таком М. отношение угловых скоростей первого и последнего валов выражается формулой:
ω 1/ ω n = (-1)n-1(m1 m2 m3…mn)/(M1 M2 M3…Mn-1)
где ω 1 — угловая скорость первого вала, ω n — угловая скорость последнего вала, n — число валов, M1M2M3…— число зубцов колес, m1m2m3…— число зубцов шестерен. Множитель (-1) n-1 стоит для того, чтобы показать, что при четном числе валов первый и последний вращаются в противоположные стороны, а при нечетном числе валов — в одну и ту же сторону. Если некоторые из валов в системе зубчатых колес подвижны, то такая система называется эпициклической. Эпициклические системы представляют чрезвычайно богатый материал для преобразования вращения. Так, например, при помощи такой системы, состоящей только из четырёх колес почти одинакового размера, можно достигнуть такой передачи, при которой на 10000 оборотов некоторой части М. другая его часть делает только один оборот.
Особый, весьма богатый класс составляют механизмы, состоящие из зубчатого колеса с острыми зубцами, круто скошенными в одну сторону и отлого в другую, и задерживающей собачки. Такие колеса называются храповыми. К этому классу относится, между прочим, соединение храпового колеса с якорем маятника в стенных часах и разные другие спуски.
Кроме твердых тел, звеньями механизмов могут быть и гибкие тела, как это мы видим в одном из распространеннейших механизмов, служащих для передачи вращения, а именно в ремённой передаче, состоящей из двух шкивов с перекинутым через них ремнем. Такие шкивы вращаются в одну сторону, если ремень на них надет просто; если же ремень надет так, что он перекрещивается между шкивами, принимая форму восьмерки, то шкивы вращаются в противоположные стороны. Отношение угловых скоростей было бы обратно пропорционально радиусам шкивов, если бы не было скольжения ремня, которое изменяет это отношение примерно на 2 процента. Часть ремня, набегающая на шкив, должна идти так, чтобы средняя линия ремня находилась в одной плоскости со средним сечением шкива. Если это условие не соблюдается, то ремень соскочит; сбегающая же со шкива часть ремня может быть отведена значительно в сторону. Этим обстоятельством пользуются при устройстве передачи между шкивами, находящимися в разных плоскостях.
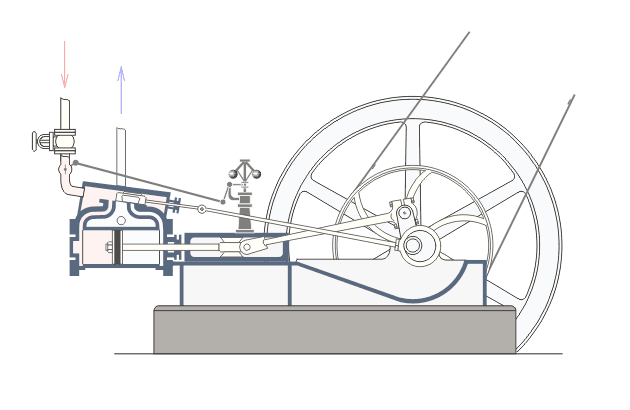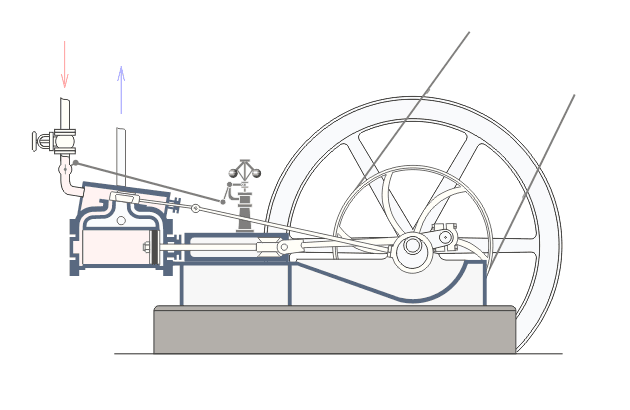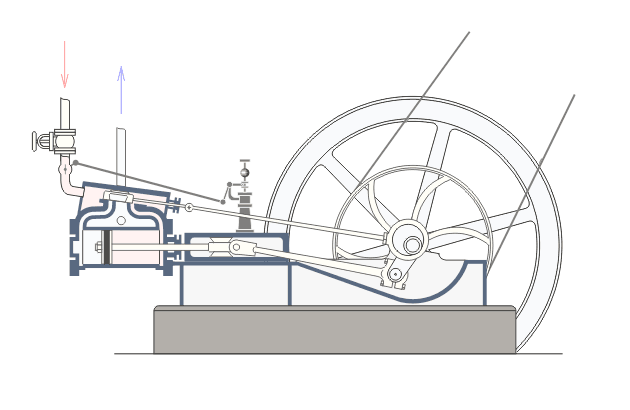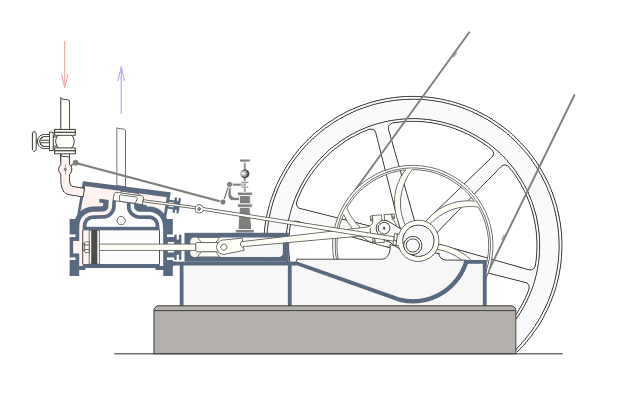
Механизмы, состоящие из твердых звенев, соединённых между собой только вращательными парами, называются шарнирными. Техника обогатилась весьма многими новыми шарнирными механизмами, в особенности за последнее столетие, благодаря стремлению разрешить поставленную в прошлом столетии Уаттом задачу о превращении движения по дуге круга в движение прямолинейное. Ватт встретился с этой задачей, усовершенствуя паровую машину и желая соединить описывающий дугу конец коромысла с прямолинейно ходящей головкой поршневого штока, и решил её изобретением своего знаменитого параллелограмма, ведущего точку по кривой, весьма мало отличающейся от прямой.
Затем было изобретено множество М., решавших ту же задачу с большим ещё приближением. Наконец, задача о приближенных прямилах получила окончательное завершение в удивительно простых и дающих весьма большое приближение прямилах Чебышева, одно из которых, может быть самое замечательное, состоит из шарнирного четырёхсторонника, в котором звено, противоположное неподвижному, представляет собой прямоугольник с равными катетами; на концах одного из катетов находятся шарниры, которыми это звено связывается с боковыми звеньями четырёхсторонника, конец же другого катета и описывает кривую, чрезвычайно мало отличающуюся от прямой; одно из боковых звеньев четырёхсторонника, производя полные обороты (непрерывное вращение), приводит механизм в движение (конечно, это звено надо вращать каким-либо двигателем). Таким образом, этот удивительный механизм, имея всего только три подвижных звена, с большим приближением преобразует в прямолинейное движение не колебание по дуге, но вращательное движение с произвольным числом полных оборотов.
В шестидесятых годах французским инженером Посселье найдено было, наконец, и точное прямило. Затем точные прямила найдены были Липкиным, Гартом и Брикаром. Хотя эти точные прямила и не так практичны, как чебышевские, будучи сложнее их, и хотя теперь головка поршневого штока парой машины ведется обыкновенно просто салазками (поступательной парой), тем не менее открытие точного прямила составило эпоху главным образом потому, что механизмы Посселье, Липкина и Гарта основаны на устройстве такой принудительной цепи, в которой произведение расстояний двух подвижных точек механизма от третьей точки остается постоянным, так что когда одно из этих расстояний увеличивается — другое уменьшается; такая кинематическая цепь называется инверсором, и при помощи её может быть решено множество кинематических и даже чисто математических задач, как, например, механическое решение уравнений высших степеней, механическое деление угла на три равные части и прочие.
Инверсор Посселье состоит из ромба с шарнирами по углам и двух равных между собой, но более длинных, чем стороны ромба, стержней, которые скреплены шарниром между собой; каждый из стержней скреплен на другом своём конце с вершинами ромба шарниром; вершины ромба, скрепленные шарнирами с длинными стержнями, суть противоположные друг другу вершины; назовем две другие вершины свободными. Расстояния, произведение которых остается постоянным, суть расстояния шарнира, в котором длинные стержни скреплены между собой, от свободных вершин ромба. Если шарнир, связывающий между собой длинные стержни, сделать неподвижным и с помощью добавочного стержня, вращающегося около неподвижного центра, вести ближайшую к точке пересечения стержней свободную вершину ромба по окружности, проходящей через шарнир, связывающий длинные стержни, то другая свободная вершина ромба и опишет прямую. Сильвестер, Кемпе, Робертс, Дарбу, Бурместер и многие другие учёные изобрели и исследовали в последнее время множество весьма интересных шарнирных механизмов, дающих замечательные преобразования траекторий. Шарнирными механизмами можно также передавать вращение даже с изменением числа оборотов, но такой способ передачи ещё не вошёл в практику, за исключением спарника, представляющего собой шарнирный параллелограмм, с помощью которого передается вращение без изменения угловой скорости от одной малой стороны параллелограмма к другой (см. Мёртвые точки).
Жидкие тела также могут служить звеньями механизма. Примером такого механизма может служить коленчатая трубка, наполненная жидкостью и снабженная в каждом колене поршнем, так как в такой системе определенному движению одного поршня будет соответствовать вполне определенное движение другого. Жидкость и прилегающие к ней стенки трубки составляют здесь кинематическую поступательную пару. Твердые звенья действуют друг на друга сопротивлением, благодаря своей твердости. Жидкие звенья, благодаря весьма малой сжимаемости жидкости, могут действовать на твердые звенья давлением; то же можно сказать и о газах. Ведь и твердые тела не абсолютно тверды, а представляют некоторую уступчивость. Поэтому Рёло рассматривает мельничное подливное колесо и действующую на него воду как высшую пару, аналогичную соединению зубчатого колеса с зубчатой линейкой (рейкой), осевую турбину и действующую на неё воду — как винтовую пару. Даже самые твердые части М. стираются трением друг о друга, а с другой стороны, например, обрабатываемая нитка передает в некоторых машинах движение от веретена к веретену. Поэтому и соединение орудия машины с обрабатываемым материалом (например, резец и обтачиваемый предмет) Рёло рассматривает как кинематическую пару, тем более что обрабатываемый предмет принимает форму огибающей различные относительные положения орудия.
С такой точки зрения разница между машиной и механизмом является только в том, что на машину смотрят с динамической точки зрения, исследуя соотношения между работой двигателя и работой полезных и бесполезных сопротивлений, а на механизм смотрят с точки зрения кинематической, исследуя соотношения между траекториями, скоростями и ускорениями. Но, например, в немецком языке такого различия нет, оба понятия обозначаются одним словом (см. Maschine)
Простые механизмы
Содержание
Трехтысячный год до нашей эры. Действо разворачивается на территории современного графства Уилтшир в Англии на живописных солсберийских равнинах.
Шумная ватага людей решительно тащит громадный тридцатитонный кремнистый песчаник, распространенную горную породу местности, в то время, как в арьергарде камне-человеко-колонны кипит основная работа: туда-сюда то и дело снуют крепкие ребята с бревнами, оперативно перекатывая и подкладывая спереди округлые деревяшки, выкатившиеся из-под камня сзади.
Короче говоря, транспортировочная суета.
Вот так, в нескольких словах можно описать процесс самой загадочной и мистической стройки человечества — процесс сооружения мегалитического Стоунхенджа.
Никому доподлинно неизвестно, кто возвел это чудо света — кельтские ли жрецы, может, древние бритты, предки современных французов, свидетели Мерлиновой бороды или инопланетяне.
Неизвестно и то, какую цель преследовали возводившие: археологи, историки и ученые всего мира до сих пор бьются над разгадками тайн постройки этого сооружения каменного века, неофициально именуемого восьмым чудом света.
Однако одно все же известно.
Наши предки, еще задолго до изобретения колеса, кое-что таки смыслили в физике. Иначе как бы им удавалось в двадцать-тридцать рук перемещать на огромные расстояния объекты массой более тридцати тонн?
Для справки. Тридцать тонн для человека — невероятная масса. К примеру, профессиональные пауэрлифтеры способны поднимать штанги порядка трехсот-четырехсот килограмм за подход. А это значит, что нам пришлось бы отправить в прошлое примерно 85 натренированных спортсменов экстра-класса, чтобы обычной тягой сдвинуть с места неолитический валун. Да, наших предков из каменного века недооценивать не стоит. Особенно их смекалку.
Что такое механизм?
История стара как мир: при меньшем получить больше.
Таков закон нашего существования в природе. Ресурсы человека ограничены, условия жизни — быстротечны и непредсказуемы, потребности — велики. А чтобы процветать и выживать, не нарушая пропорции данных трех переменных, необходимо умение не только подстраиваться, но и использовать с умом то, что дано. В конце концов, умение облегчить себе труд и превысить мышечные возможности — это то, что выделяет нас на фоне других представителей царства животных.
Именно поэтому технологические решения всегда развивались параллельно с человеком. Мы всегда были, есть и будем в поиске. В поиске того, что могло бы помочь нам выгадывать больше, вкладываясь меньше. И практически все, что мы придумывали во имя этой цели на протяжении тысячелетий, так или иначе можно отнести к понятию механизма.

Механизм — это устройство, повышающее производительность труда и облегчающее его выполнение. Задача его проста — преобразовывать энергию и передавать движение: к механизму прикладывается сила, которую он в свою очередь «перерабатывает» и передает телу, совершая работу. Обычно наименьший неделимый элемент механизма называется простым или простейшим.
Ему можно дать следующее краткое определение:
Простой механизм — устройство, служащее для преобразования силы.
Механизмы помогают нам везде. Начать с того, что в скелете человека все кости, имеющие свободный ход, являются «простыми механизмами» — рычагами. Продолжить можно чем угодно, хоть содержимым кухонного шкафчика: ножи, топорики для рубки мяса, открывашки, штопоры, ножницы и прочее — все это имеет отношение к простым механизмам. Двери, окна, тележки в супермаркетах, качели, пандусы, пинцеты, ручки смесителя в ванной, колодца, велосипеды, внутренности ремонтного ящика, от гвоздодера до кусачек… продолжать можно долго. Простые механизмы — основа нашей жизни.
Основы простых механизмов
По математике формул очевидно, что с увеличением расстояния перемещения, сила, необходимая для совершения того же объема работы, уменьшается.
К тому же, так как сила — вектор, с помощью механизма мы можем изменять не только ее величину, но и направление.

Принцип: пройти два лишних метра, затратив при этом меньше мышечных сил.
Флаг тридцать тонн не весит, но с помощью механизма мы задали силе противоположное направление и немного выиграли — лезть никуда не придется.
Принцип механического выигрыша
«Немного выиграли» — вся суть механизмов. Благодаря простым механическим устройствам мы меняем направление силы, расстояние ее применения, непосредственно значение силы и все ради того, чтобы получить выигрыш в силе.
Определить выигрыш с точки зрения физики можно так:
Механический выигрыш — величина увеличения силы, получаемая в результате работы простого механизма.
Величина работы никогда не меняется — меняется либо сила, либо расстояние. Выигрыш рассчитывается отношением двух сил:
Виды простых механизмов
Простые механизмы по своей конструкции делятся на два типа: рычаг и наклонная плоскость.
У рычага встречается две разновидности — блок и ворот. Наклонная плоскость так же встречается с двумя разновидностями — винтом и клином.
Ну, чисто технически вы будете правы, если скажете, что мир устроен и построен на шести простых механизмах.
Рычаг
Рычаг. Представляет собой перекладину, которая вращается вокруг неподвижной точки опоры. Рычаг помогает поднимать тяжелые предметы, уравновешивать их. Пример простого рычага — качели-балансиры.
Блок. Разновидность рычага. В простом понимании представляет собой веревку, намотанную на колесо.
Облегчает работу тем, что меняет направление силы. К тому же, тянут веревку обычно вниз, поднимая тем самым груз наверх. А это значит что? Правильно: нам еще и помогает сила тяжести.
Ворот
Ворот. Тоже разновидность рычага. Механизм принципа «ось-колесо». Ось — цилиндр, который фиксирует колесо на месте, а колесо на этой оси вращается.
Входная сила прикладывается к оси, давая выходную силу в виде вращательного движения колеса. Вспомните велосипед: чем активнее вы нажимаете на педаль, тем быстрее двигаетесь.
Наклонная плоскость
Наклонная плоскость. Ранее упомянутый нами в примере лестничный проем — яркий пример того, как выглядит механизм по типу наклонной плоскости.
Это поверхность, у которой один край расположен выше другого. Кстати, именно в наклонных плоскостях кроется секрет постройки древних пирамид Египта.
Винт. Если взять наклонную плоскость, обернуть ее вокруг цилиндра, то мы получим винт — механизм, который используется для того, чтобы что-то опускать, поднимать или обычно просто дабы удерживать два тела вместе.
Типичная крышка от банки или бутылки — показательный пример винта. А вот вкрутить даже маленький винтик — задача времязатратная, поскольку винтовые механизмы значительно увеличивают расстояние применения силы. Чтобы сравнить, можно взять два винта и кусок поролона: один винт в него вдавить, другой вкрутить. А теперь попробуйте вдавить винт в стену…
Клин. Если представить две наклонные плоскости, сходящиеся в одной точке, выйдет то, что называется клином.
Он помогает удерживать предметы на месте, но, что важнее, раскалывать тела или отделять от них части.
Это интересно: почему говорят «клин клином вышибают»?
Этимология фразеологизма тесно связана с тем, как в старину раскалывали массивные бревна.
Одним клином с такой задачей было не справиться: забитый до упора, он лишь частично раскалывал бревно.
Ни клин не достать обратно, ни дров не нарубить. Поэтому рядом с забитым клином вбивали рядом другой — так, чтобы второй заходил глубже и вышибал первый. И так далее, и тому подобное, до тех пор, пока деревянный брусок не расколется напополам.
Вот и выходит, что клин клином вышибают в прямом смысле — один клин вышибают вторым. И откуда только взялась распространенная речевая ошибка «клин клином вышибает»?
Итоги
Так что же, простые механизмы насколько эффективны, что знаменитая архимедова «угроза» про переворот Земли — правда?
Немного математической магии рычагов, о которой вы узнаете совсем скоро, и… выходит один миллион триллионов километров, он же квинтиллион.
Подсказка: возраст Земли — четыре с половиной миллиарда лет. Так вот, пока Архимед будет двигать свой рычаг, Земля успеет пережить более 6000 циклов идущих друг за другом Больших взрывов и апокалипсисов.
Да и дали бы мы Архимеду точку опоры, пусть так. Вопрос в другом: как сконструировать рычаг такой неимоверной длины в земных условиях?
А как же его после переместить в космическое пространство?