Для чего нужен расширенный алгоритм евклида

Расширенный алгоритм Евклида

Вы будете перенаправлены на Автор24

Расширенный алгоритм Евклида — это алгоритм определения коэффициентов, позволяющих выразить наибольший общий делитель числовой пары через эти два числа.

Введение

Под алгоритмом Евклида понимается разработанный им алгоритм, позволяющий определить наибольший общий делитель целочисленной пары.

Древнегреческий математик Евклид жил в третьем веке до нашей эры. Он описал этот алгоритм в своей серии книг, называемых «Начала».

Данный алгоритм является старейшим числовым алгоритмом, который применяется и в настоящее время.

Для наипростейшего варианта применения алгоритма Евклида, берутся два целых положительных числа, и с помощью этого алгоритма находится ещё два числа, состоящие из числа меньшего веса и разности этих чисел. Эта операция циклически выполняется до тех пор, пока числа не сравняются. Полученное в итоге число и будет наибольшим общим делителем изначальной пары чисел. Евклид разработал алгоритм применительно лишь к натуральным числам и геометрическим понятиям, таким как длина, площадь, объём. Но в девятнадцатом веке нашей эры его обобщили и на другие математические понятия, например, целые Гауссовы числа и полиномы одной переменой. Дальнейшее развитие алгоритма вызвало внедрение термина евклидово кольцо. Затем алгоритм Евклида обобщили и на такие понятия математики как узлы и многомерные полиномы. Алгоритм нашёл много внедрений в области теории и практики. Например, на его базе создан криптографический алгоритм с открытым ключом RSA, который применяется в коммерческой сфере.

Расширенный алгоритм Евклида

$a • x + b • y = gcd (a, b)$.

($b$%$a • X_1 + a • Y_1 = g$,

и надо найти решение ($x, y$) для искомой пары ($a, b$):

Выполнив ряд преобразований, находим конечные формулы:

Источник

Расширенный алгоритм Евклида

Алгоритм вычисления наибольшего общего делителя (НОД) был открыт древнегреческими математиками и известен как алгоритм “взаимного вычитания”. И хотя упоминание об этом алгоритме имеется еще у Аристотеля, впоследствии его стали называть алгоритмом Евклида. Что такое наибольший общий делитель, его свойства и методы вычисления рассмотрены в [1].

Напомним, что НОД двух чисел можно вычислить согласно следующей рекуррентности:

На языке Си процедура вычисления НОД имеет вид:

int gcd( int a, int b)

Алгоритм Евклида можно расширить для нахождения по заданным a и b таких целых x и y, что ax + by = d, где d – наибольший общий делитель a и b.

Лемма. Пусть для положительных целых чисел a и b (a > b) известны d = НОД(a, b) = НОД(b, a mod b), а также числа x’ и y’, для которых

Тогда значения x и y, являющиеся решениями уравнения ax + by = d, находятся из соотношений

x = y’, y = x’ – y’ · (2)

Через здесь обозначена целая часть числа a/b.

Доказательство. Поскольку a mod b = a – · b, то

d = x’ · b + y’ · (a – · b) = y’ · a + (x’ – y’ · ) · b = x · a + y · b,

где обозначено x = y’, y = x’ – y’ · .

Функция gcdext(int a, int b, int *d, int *x, int *y), приведенная ниже, по входным числам a и b находит d = НОД(a, b) и такие x, y что d = a · x + b · y. Для поиска неизвестных x и y необходимо рекурсивно запустить функцию gcdext(b, a mod b, d, x, y) и пересчитать значения x и y по выше приведенной формуле. Рекурсия заканчивается, когда b = 0. При b = 0 НОД(a, 0) = a и a = a · 1 + 0 · 0, поэтому полагаем x = 1, y = 0.

void gcdext ( int a, int b, int *d, int *x, int *y)

Для ручного выполнения расширенного алгоритма Евклида удобно воспользоваться таблицей с четырьмя столбцами (как показано ниже в примере), соответствующих значениям a, b, x, y. Процесс вычисления разделим на три этапа:

а) Сначала вычислим НОД(a, b), используя первые два столбца таблицы и соотношение (1). В последней строке в колонке а будет находиться значение d = НОД(a, b).

б) Занесем значения 1 и 0 соответственно в колонки x и y последней строки.

в) Будем заполнять последовательно строки для колонок x и y снизу вверх. Значения x и y в последнюю строку уже занесены на этапе б). Считая, что в текущей заполненной строке уже находятся значения (x’, y’), мы при помощи формул (2) будем пересчитывать и записывать значения (x, y) в соответствующие ячейки выше стоящей строки.

1. Расширенный алгоритм Евклида. Найдем решение уравнения 5x + 3y = 1. Вычисление НОД(5, 3) и нахождение соответствующих x, y произведем в таблице:

Порядок и направление вычислений указаны стрелками и буквами.

y = x’ – y’ · = 1 – (-1) · = 1 + 1 = 2

Линейным сравнением называется уравнение вида ax = b (mod n). Оно имеет решение тогда и только тогда, когда b делится на d = НОД(a, n). Если d > 1, то уравнение можно упростить, заменив его на a’x = b’ (mod n’), где a’ = a / d, b’ = b / d, n’ = n / d. После такого преобразования числа a’ и n’ являются взаимно простыми.

Алгоритм решения уравнения a’x = b’ (mod n’) со взаимно простыми a’ и n’ состоит из двух частей:

1. Решаем уравнение a’x = 1 (mod n’). Для этого при помощи расширенного алгоритма Евклида ищем решение (x₀, y₀) уравнения a’x + n’y = 1. Взяв по модулю n’ последнее равенство, получим a’x₀ = 1 (mod n’).

Лемма. Если НОД(k, m) = 1, то равенство ak = bk (mod m) эквивалентно a = b (mod m).

Доказательство. Из ak = bk (mod m) следует, что (a – b) · k делится на m. Но поскольку k и m взаимно просты, то a – b делится на m, то есть a = b (mod m).

Пример. Решить уравнение 18x = 6 (mod 8).

ДИОФАНТОВЫ УРАВНЕНИЯ

Диофантовыми называются уравнения вида

В этой главе рассмотрим алгоритм нахождения решения линейного диофантового уравнения с двумя неизвестными вида a·x + b·y = c (далее для простоты будем опускать знаки умножения и писать прото ax + by = c).

Теорема 1. Уравнение ax + by = c имеет решение в целых числах тогда и только тогда, когда c делится на НОД(a, b).

Теорема 2. Если пара (x₀, y₀) является решением уравнения ax + by = c, то все множество его решений (x, y) описывается формулой:

Для нахождения частичного решения (x₀, y₀) уравнения ax + by = c следует сначала найти решение (x’, y’) уравнения ax + by = d (d – наибольший общий делитель a и b) при помощи расширенного алгоритма Евклида, после чего умножить его на c / d. То есть

Пример. Найти множество решений уравнения 5x + 3y = 7.

1. Уравнение имеет решение, так как 7 делится на НОД(5, 3) = 1.

2. Находим решение уравнения 5x’ + 3y’ = 1 при помощи расширенного алгоритма Евклида: (x’, y’) = (-1, 2).

3. Находим решение (x₀, y₀) исходного диофантового уравнения:

Согласно теореме 2 множество решений исходного диофантового уравнения имеет вид:

СПИСОК ЛИТЕРАТУРЫ

1. Статья «Наибольший общий делитель «, журнал Потенциал №10, 2008.

Источник

СОДЕРЖАНИЕ

Описание

Расширенный алгоритм Евклида действует аналогично, но добавляет две другие последовательности, как показано ниже.

Это означает, что пара коэффициентов Безу, предоставляемая расширенным алгоритмом Евклида, является минимальной парой коэффициентов Безу, поскольку это единственная пара, удовлетворяющая обоим вышеупомянутым неравенствам.

Пример

Доказательство

Таким образом, и являются коэффициентами Безу. s k <\ displaystyle s_ > т k <\ displaystyle t_ >

Рекуррентное соотношение можно переписать в матричном виде

Полиномиальный расширенный алгоритм Евклида

Второе отличие заключается в ограничении размера коэффициентов Безу, обеспечиваемом расширенным алгоритмом Евклида, который более точен в полиномиальном случае, что приводит к следующей теореме.

Третье отличие состоит в том, что в полиномиальном случае наибольший общий делитель определяется только с точностью до умножения на ненулевую константу. Существует несколько способов однозначного определения наибольшего общего делителя.

Псевдокод

Для реализации описанного выше алгоритма следует сначала заметить, что на каждом шаге нужны только два последних значения индексированных переменных. Таким образом, для экономии памяти каждая индексированная переменная должна быть заменена всего двумя переменными.

и аналогично для других параллельных заданий. Это приводит к следующему коду:

Частное a и b по их наибольшему общему делителю, которое выводится, может иметь неправильный знак. Это легко исправить в конце вычислений, но здесь не было сделано для упрощения кода. Точно так же, если либо a, либо b равны нулю, а другое отрицательно, наибольший общий делитель, который выводится, отрицателен, и все знаки вывода должны быть изменены.

Однако во многих случаях это не совсем оптимизация: в то время как первый алгоритм не подвержен переполнению при использовании с машинными целыми числами (то есть целыми числами с фиксированной верхней границей цифр), умножение old_s * a при вычислении bezout_t может переполняться, ограничивая эту оптимизацию входными данными, которые могут быть представлены в менее чем половине максимального размера. При использовании целых чисел неограниченного размера время, необходимое для умножения и деления, увеличивается квадратично с размером целых чисел. Это означает, что «оптимизация» заменяет последовательность умножений / делений малых целых чисел на единичное умножение / деление, что требует больше вычислительного времени, чем операции, которые она заменяет вместе взятые.

Упрощение дробей

Вычисление мультипликативных обратных в модульных структурах

Модульные целые числа

Тождество Безу утверждает, что a и n взаимно просты тогда и только тогда, когда существуют целые числа s и t такие, что

Сокращение этого тождества по модулю n дает

Простые алгебраические расширения полей

Пример

Случай более двух чисел

Итак, чтобы применить к n числам, мы используем индукцию

Источник

Алгоритм Евклида

Вы будете перенаправлены на Автор24

Существуют разные способы поиска НОД. Одним из наиболее эффективных из них является алгоритм Евклида для вычисления наибольшего общего делителя. Рассмотрим его подробнее.

Алгоритм Евклида для нахождения НОД — это последовательное деление с остатком.

На каждом этапе нахождения НОД с помощью алгоритма Евклида производится деление большего из пары двух чисел на меньшее, а остаток записывается и используется при дальнейших вычислениях в качестве нового делителя для предыдущего.

Вычисление остатка производят до тех пор, пока он не будет равен нулю, тогда последний использованный делитель и будет являться наибольшим общим делителем, полученным через алгоритм Евклида.

$НОД(f_0, f_1)= НОД(f_1, f_2)$

То есть применение алгоритма Евклида для нахождения наибольшего общего делителя есть не что иное, как последовательная цепочка вычислений остатков и частных от деления.

Цепочку вычисления НОД с помощью алгоритма Евклида можно записать так:

$f_0=a_1 \cdot f_1 + f_2$;

$f_1=a_2 \cdot f_2 + f_3$;

Каждое последовательное вычисление нового остатка называется итерацией.

Рисунок 1. Алгоритм Евклида: блок-схема. Автор24 — интернет-биржа студенческих работ

Готовые работы на аналогичную тему

Рассмотрим пример на получение НОД через алгоритм Евклида.

При вычислении НОД получаем последовательно пары чисел:

Алгоритм Евклида: доказательство

Докажем корректность алгоритма Евклида с помощью двух этапов.

$f_=q_f_+f_$, так как он является делителем обоих слагаемых в правой части равенства.

НОД: расширенный алгоритм Евклида

Расширенный алгоритм Евклида рассматривает НОД через линейную комбинацию этих чисел с некоторыми целыми коэффициентами.

Здесь остатки вычисляются по следующим формулам:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 29 03 2021

Источник

Расширенный алгоритм Евклида

Алгори́тм Евкли́да — алгоритм для нахождения наибольшего общего делителя двух целых чисел или наибольшей общей меры двух однородных величин.

Содержание

История

Древнегреческие математики называли этот алгоритм ἀνθυφαίρεσις или ἀνταναίρεσις — «взаимное вычитание». Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля. В «Началах» Евклида он описан дважды — в VII книге для нахождения наибольшего общего делителя двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков.

Историками математики (Цейтен и др.) было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника). Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.

Ряд математиков средневекового Востока (Сабит ибн Курра, ал-Махани, Ибн ал-Хайсам, Омар Хайям) попытались построить на основе алгоритма Евклида теорию отношений, альтернативную по отношению теории отношений Евдокса, изложенной в V книге «Начал» Евклида. Согласно определению, предложенному этими авторами, четыре величины, первая ко второй и третья к четвёртой, имеют между собой одно и то же отношение, если при последовательном взаимном вычитании второй величин в обеих парах на каждом шаге будут получаться одни и те же неполные частные.

Алгоритм Евклида для целых чисел

Пусть a и b целые числа, не равные одновременно нулю, и последовательность чисел

определена тем, что каждое r_k это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело, то есть

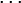
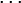
a = bq₀ + r₁ b = r₁q₁ + r₂ r₁ = r₂q₂ + r₃ r_{k − 2} = r_{k − 1}q_{k − 1} + r_k r_{n − 1} = r_nq_n

Корректность этого алгоритма вытекает из следующих двух утверждений:

Проще сформулировать алгоритм Евклида так: если даны натуральные числа a и b и, пока получается положительное число, по очереди вычитать из большего меньшее, то в результате получится НОД.

Расширенный алгоритм Евклида и соотношение Безу

Формулы для r_i могут быть переписаны следующим образом:

здесь s и t целые. Это представление наибольшего общего делителя называется соотношением Безу, а числа s и t — коэффициентами Безу. Соотношение Безу является ключевым в доказательстве леммы Евклида и основной теоремы арифметики.

Связь с цепными дробями

Отношение a / b допускает представление в виде цепной дроби:

.

.

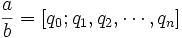
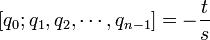
Вариации и обобщения

Ускоренные версии алгоритма

См. также

Литература

Полезное

Смотреть что такое «Расширенный алгоритм Евклида» в других словарях:

Алгоритм Евклида — Имеется викиучебник по теме « … Википедия

Евклида алгоритм — Алгоритм Евклида алгоритм для нахождения наибольшего общего делителя двух целых чисел или наибольшей общей меры двух однородных величин. Содержание 1 История 2 Алгоритм Евклида для целых чисел … Википедия

Алгоритм Шенкса — (англ. Baby step giant step; также называемый алгоритм больших и малых шагов) в теории групп, детерминированный алгоритм дискретного логарифмирования в кольце вычетов по модулю простого числа. Для модулей специального вида данный… … Википедия

Алгоритм Фюрера — (англ. Fürer’s algorithm) быстрый метод умножения больших целых чисел. Алгоритм был построен в 2007 году швейцарским математиком Мартином Фюрером[1] из университета штата Пенсильвания как асимптотически более быстрый алгоритм, чем его… … Википедия

Код Боуза — Коды Боуза Чоудхури Хоквингхема (БЧХ коды) в теории кодирования это широкий класс циклических кодов, применяемых для защиты информации от ошибок (см. Обнаружение и исправление ошибок). Отличается возможностью построения кода с… … Википедия

Список алгоритмов — Эта страница информационный список. Основная статья: Алгоритм Ниже приводится список алгоритмов, группированный по категориям. Более детальные сведения приводятся в списке структур данных и … Википедия

Программируемые алгоритмы — Служебный список статей, созданный для координации работ по развитию темы. Данное предупреждение не устанавл … Википедия

Китайская теорема об остатках — Несколько связанных утверждений известны под именем китайской теоремы об остатках. Эта теорема в её арифметической формулировке была описана в трактате китайского математика Сунь Цзы «Сунь Цзы Суань Цзин» (кит. упр. 孙子算经, пиньинь: sunzi suanjing) … Википедия

Метод квадратичных форм Шенкса — метод факторизации целых чисел, основанный на применении квадратичных форм, разработанный Даниелем Шенксом (англ. Daniel Shanks).[1] в 1975 году, как развитие метода факторизации Ферма. Для 32 разрядных компьютерах алгоритмы, основанные на… … Википедия

Тест простоты Люка — В теории чисел тест простоты Люка это тест простоты натурального числа n; для его работы необходимо знать разложение на множители. Для простого числа n простые множители числа вместе с некоторым основанием a составляют сертификат Пратта, который… … Википедия

Источник