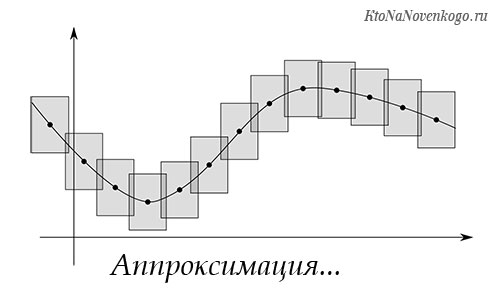
Для чего нужна аппроксимация
ТЕМА 3. АППРОКСИМАЦИЯ ФУНКЦИЙ
3.1. Зачем нужна аппроксимация функций?
В практике расчетов, связанных с обработкой экспериментальных данных, вычислением f(x), разработкой вычислительных методов, встречаются следующие две ситуации:
В зависимости от способа подбора параметров получают различные методы аппроксимации; наибольшее распространение среди них получили интерполяция и среднеквадратичное приближение, частным случаем которого является метод наименьших квадратов.
3.2. Что такое интерполяция?
В случае линейной аппроксимации (3.1) система для нахождения коэффициентов линейна и имеет следующий вид:
Для большинства практически важных приложений при интерполяции наиболее удобны обычные алгебраические многочлены, ибо они легко обрабатываются.
Общий вид алгебраического многочлена
Матрица системы (3.2) в этом случае имеет вид
и ее определитель (это определитель Вандермонда) отличен от нуля, если точки x i разные. Поэтому задача (3.2) имеет единственное решение, т.е. для заданной системы различных точек существует единственный интерполяционный многочлен.
3.3. Какие бывают многочлены и способы интерполяции?
Интерполяционный многочлен Ньютона (PN)
Здесь текущая точка, в которой надо вычислить значение многочлена, разделенные разности порядка k, которые вычисляются по следующим рекуррентным формулам:
Схема расчета многочлена Ньютона представлена на рис. 3.2.
Линейная (PNL) и квадратичная(PNS) интерполяция
и за значение f(x) принимают ( линейная интерполяция ) или ( квадратичная интерполяция ). Схема расчета для линейной и квадратичной интерполяции приведена на рис. 3.3.
Интерполяционный многочлен Лагранжа (PL)
Схема расчета интерполяционного многочлена Лагранжа представлена на рис. 3.4.
Интерполяция общего вида, использующая прямое решение системы (3.2) методом Гаусса (POG)
Поэтому когда требуется производить много вычислений многочлена, построенного по одной таблице, оказывается выгодно вначале один раз найти коэффициенты и затем использовать формулу (3.3). Коэффициенты находят прямым решением системы (3.2) c матрицей (3.4), затем вычисляют его значения по экономно программируемой формуле (алгоритм Горнера)
Схема расчета интерполяционного многочлена общего вида по формуле (3.9) с прямым решением системы (3.2) приведена на рис.3.5.
Интерполяция общего вида, использующая расчет коэффициентов многочлена (3.3) через многочлен Лагранжа (POL)
Находить коэффициенты многочлена (3.3) можно, не решая прямо систему (3.2), а используя разложение коэффициентов Лагранжа (3.8):
Рекуррентные формулы для нахождения коэффициентов :
Схема алгоритма вычисления коэффициентов многочлена общего вида по формулам (3.10), (3.11) представлена на рис. 3.6.
3.4. Что такое среднеквадратичная аппроксимация?
Суть среднеквадратичной аппроксимации заключается в том, что параметры функции подбираются такими, чтобы обеспечить минимум квадрата расстояния между функциями f(x) и в пространстве (см. подразд. 1.3), т.е. из условия
В случае линейной аппроксимации (3.1) задача (3.12) сводится к решению СЛАУ для нахождения необходимых коэффициентов :
Здесь скалярные произведения в L 2.
Матрица системы (3.13) симметричная, и ее следует решать методом квадратного корня.
Тогда матрица СЛАУ (3.13) диагональная и параметры находятся по формуле
Метод наименьших квадратов (МНК)
получаем систему n линейных уравнений относительно n неизвестных следующего вида:
Здесь векторы-таблицы функ-ций. Элементы матрицы G и вектора в (3.15) определяются выражениями
скалярные произведения векторов.
Система (3.15) имеет симметричную матрицу G и решается методом квадратного корня.
Схема расчета коэффициентов многочлена вида (3.3) по методу наименьших квадратов представлена на рис. 3.8.
Составляем сумму квадратов невязок
Условия минимума (3.1 4 ):
Приводя подобные члены, получим окончательно систему двух уравнений с симметричной матрицей относительно неизвестных c 1 и c 2 :
На рис. 3.9 приведена таблица функции f(x) и полученная по МНК функция ( x ).
3.5. Варианты заданий
Что такое аппроксимация
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Многие термины, используемые точными науками, находят свое применение и в обыденной жизни.
Сегодня рассмотрим один из них, термин «аппроксимация».
Узнаем, что такое аппроксимация в математике и в каких ситуациях это понятие можно использовать, исключая точные науки.
Аппроксимация в математике — это …
Как правило, суть термина раскрывается, если его перевести на родной язык. В переводе с латинского «proxima» – это «ближайшая», более широкое толкование перевода – «приближение».
Следовательно, аппроксимация – это метод вычислений, используемый в математике, заключающийся в том, что сложные математические объекты при расчетах (других исследованиях) заменяются более простыми (но максимально похожими).
Пример: при расчетах, в которых используются иррациональные числа (бесконечные десятичные дроби), эти числа заменяются рациональными числами (конечными дробями), приближенными по количественному значению. Этот метод называется диофантовым приближением и является примером применение метода аппроксимации.
Знакомое нам всем число π (пи) – это бесконечная десятичная дробь. π = 3,1415926535897932 …. При вычислениях, в которых используется число «пи», принято брать не дробь целиком (но это и невозможно, ведь она бесконечна), а только 2 цифры после запятой.
Таким образом, принято считать, что π = 3,14. И это тоже применение метода аппроксимации.
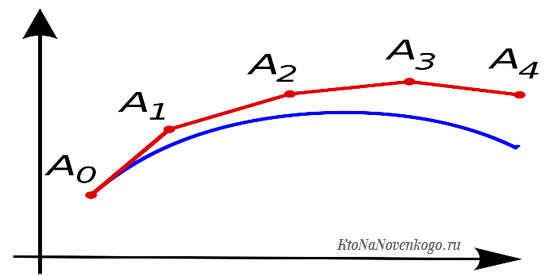
В геометрии метод аппроксимации используется в действиях с кривыми: для удобства вычислений они заменяются ломаными. Как это выглядит, можно посмотреть на схеме:
Кривая (синий цвет) для проведения каких-либо вычислений аппроксимируется в ломаную, каждое из звеньев которой имеет вершины с координатами, максимально приближенными к координатам кривой.
Термин «аппроксимация» схож по сути со следующими математическими понятиями:
Применение термина «аппроксимация» в иных областях
Суть термина применительно к философским категориям остается той же, что и в математике – это указание на приблизительный характер какого-либо процесса, явления.
Аппроксимация в экономике – это метод, используемый в моделировании экономических ситуаций, а именно – замена сложных производственных или иных экономических объектов более простыми (при сохранении основных входных и выходных параметров этих объектов).
Данный метод позволяет решать сложные задачи с помощью «пожертвования» деталями, что делает алгоритм решения (это что?) более простым.
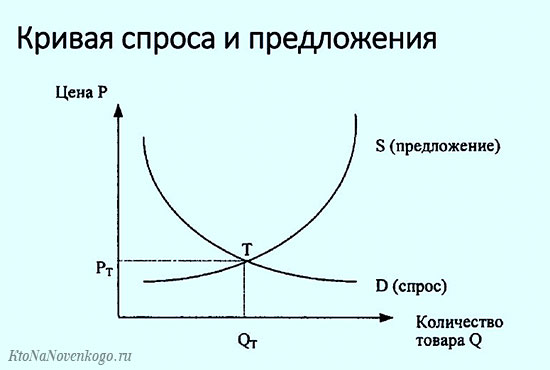
Приведу простой пример: для построения кривых спроса (что это?) и предложения используются показатели цены и количества проданных товаров. Это наглядно изображено на рисунке ниже:
На самом деле на спрос и предложение влияние оказывают и другие факторы.
При проведении анализа эти факторы не учитывают, принимая во внимание только цену и проданный товар, следовательно, построенные кривые являются аппроксимацией более сложных кривых. Но для оценки данной экономической ситуации полученные аппроксимированные графики являются достаточными.
Аппроксимация в повседневной жизни – это обобщение ряда событий, имеющих одинаковый посыл. Например, на вопрос: «Как дела?», мы чаще всего отвечаем: «Нормально, все в порядке».
Это аппроксимация оценки своей жизни, своей деятельности за недавний отрезок времени. На самом деле происходило и плохое, и хорошее, но в целом – «все по среднему», мы не вдаемся в подробности и не рассказываем, что произошло за, допустим, последнюю неделю.
Или еще пример: вчера весь день светило солнце, несколько раз «занавешиваясь» облачками. Но на вопрос о погоде мы ответим, что было солнечно, и не будем рассказывать о ее небольших изменениях, потому что они были недолгими, и не существенными.
Краткое резюме
Мы рассмотрели применение термина «аппроксимация» в различных областях. Следует отметить, что практическое использование аппроксимации в алгебре и геометрии очень специфично, поэтому в этой статье детального разъяснения нет.
Для тех, кто хочет подробней узнать про аппроксимацию функций привожу 2 ссылки: первая – лекция общего характера, другая – монография по этой же теме с прикладным уклоном.
Читайте наш блог, это познавательно!
Автор статьи: Елена Копейкина
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
Комментарии и отзывы (2)
Мне думается, математики, социологи, маркетологи и проч. знают этот термин. Всем же прочим просто не нужно такое специфическое слово. Ну как его использовать вне профессиональной сферы?
Происхождение этого слова я вижу от английского «approximately», что означает «приблизительно». Оно в свою очередь от другого слова, кстати очень распространенный термин в авиации — «approach», то есть приближение, подход.
Аппроксимация
Добавлено в закладки: 0
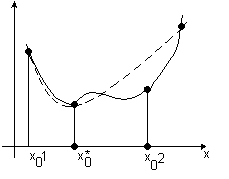
Метод аппроксимации дает возможность проводить исследования разных характеристик объектов, например, их качественных и числовых свойств.
Это достигается тем, что эти свойства сводятся к характеристикам объектов, которые уже известны, или гораздо легче определяются.
Рассмотрим, более детально, ч то значит аппроксимация. Аппроксима́ция, или приближе́ние являются научным методом, состоящим в замене одних объектов другими, в каком-то смысле близкими к исходным, однако более простыми.
Аппроксимация дает возможность исследовать качественные свойства и количественные характеристики объекта, сводя задачу к изучению более удобных или более простых объектов (к примеру, таких, свойства которых легко вычисляются или свойства которых известны уже). В теории чисел изучают диофантовы приближения, в частности, приближения рациональными иррациональных чисел. В геометрии рассматривают аппроксимации кривых ломаными. Определенные разделы математики целиком посвящены в сущности аппроксимации, к примеру, теория приближения функций, количественные методы анализа.
В переносном смысле употребляют в философии как способ приближения, указание на неокончательный, приблизительный характер. К примеру, в таком смысле термин «аппроксимация» употреблялся активно Сёреном Кьеркегором (1813—1855) в «Заключительном ненаучном послесловии…»
Остаточный член
Остаточный член — разница меж аппроксимирующей функцией и заданной функцией. Оценка остаточного члена тем самым является оценкой точности рассматриваемой аппроксимации. Данный термин используется, к примеру, в формуле ряда Тейлора.
Примеры
Когда функция будет применяться лишь для интерполяции, то достаточно аппроксимировать точки полиномом, скажем, пятой степени:
Гораздо сложней обстоит дело, когда изменения с граничными условиями. Тут уже качество итога зависит от профессионализма исследователя.
Для оптимального выбора параметров уравнений используют обычно способ наименьших квадратов.
Мы надеемся, что да ли наиболее полное определение и понятие термина аппроксимация, привели ее примеры
АППРОКСИМАЦИЯ
Смотреть что такое «АППРОКСИМАЦИЯ» в других словарях:
Аппроксимация — (approximation приближение) процедура выбора оптимальной аппроксимирующей функции из определенного класса функций. Следует различать параметрическую и непараметрическую аппроксимацию. При параметрической аппроксимации общий вид (формула, модель)… … Официальная терминология
АППРОКСИМАЦИЯ — [ Словарь иностранных слов русского языка
аппроксимация — приближение; апроксимирование, апроксимация, линеаризация Словарь русских синонимов. аппроксимация сущ., кол во синонимов: 3 • апроксимация (2) • … Словарь синонимов
аппроксимация — и, ж. approximation, нем. Approximation <лат. approximare приближаться. мат. Приближенное выражение каких л. величин через другие, более простые величины. Крысин 1998. | Аппроксимация называется официальное снижение требований в школьной… … Исторический словарь галлицизмов русского языка
Аппроксимация — приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач. В экономике целью А. часто является укрупнение характеристик моделируемых экономических объектов. Словарь бизнес терминов. Академик.ру.… … Словарь бизнес-терминов
АППРОКСИМАЦИЯ — (от лат. approximo приближаюсь) замена одних математических объектов (напр., чисел или функций) другими, более простыми и в том или ином смысле близкими к исходным (напр., кривых линий близкими к ним ломаными) … Большой Энциклопедический словарь
АППРОКСИМАЦИЯ — приближенное выражение математических величин (чисел, функций и т. п.) через другие. Любую непрерывную функцию f(x), a ≤ х ≤ b можно аппроксимировать алгебраическими или тригонометрическими многочленами. Важно определить степень… … Геологическая энциклопедия
АППРОКСИМАЦИЯ — (от лат. approximare – приближаться). Обучение иноязычному произношению, ограниченное приближением к правильному произношению и допускающее «снисходительное отношение» к фонетическим ошибкам, не нарушающим коммуникацию. Однако А. не должна… … Новый словарь методических терминов и понятий (теория и практика обучения языкам)
Аппроксимация — [approximation] «замена одних математических объектов другими, в том или ином смысле близкими к исходным»[1] ; в частности приближенное выражение сложной функции с помощью более простых. Например, при кусочно линейной А., непрерывная… … Экономико-математический словарь
аппроксимация — «Замена одних математических объектов другими, в том или ином смысле близкими к исходным» [1]. В частности — приближенное выражение сложной функции с помощью более простых. Например, при кусочно линейной А., непрерывная… … Справочник технического переводчика
Аппроксимация
«Что такое аппроксимация?» – один из нередко задаваемых в сети интернет вопросов. Жаждущие получить ответ, обычно хотят его иметь в форме: точной, всеобъемлющей и короткой. О содержательности ответа как-то забывают.
Если спросить: «Что такое музыка?», то я, как дилетант, скажу, что музыка – это то, что приятно слушать. А профессионал возможно будет поставлен в тупик таким «простым» вопросом. Однако, ближе к теме.
Аппроксимация – это приближение. Приближение чего-то к чему-то с той или иной точностью. Более пространно: аппроксимация, как процесс, – это построение объекта, с той или иной точностью воспроизводящего те или иные свойства исходного, т.е. аппроксимируемого, объекта. Причем, построение объекта в том или ином отношении более удобного, чем исходный объект.
У аппроксимации может быть множество направлений и приложений. Я могу кратко рассказать о той аппроксимации, которой занимался десятки лет. Более всего, это относилось к процессам топливоиспользования на ТЭС. Десятки, а порой и сотни, разных графиков и таблиц, характеризующих работу энергетического оборудования, приходилось переводить в форму аппроксимирующих уравнений или формул. То есть, одни математические объекты – графики и таблицы – воспроизводились другими математическими объектами – аппроксимирующими формулами. После чего формулы заводились на ЭВМ или персональный компьютер, и по ним можно было получить все нужные выходные данные, не водя пальцем по исходным графикам или делая какие-то грубые оценки по таблицам.
Кроме этого, мне, как программисту (или алгоритмисту), приходилось создавать довольно сложные программы – модели, описывающие технологический процесс. Порой эти программы были весьма неудобны для обычного пользователя. Но полученные расчетным путем данные вполне удавалось воспроизвести достаточно точной и простой в обращении аппроксимирующей формулой.
Вы можете в Excel построить график и щелкнуть по нему правой кнопкой мыши. Появится запрос: Вставить линию тренда. Там же можно будет разместить на графике и уравнение тренда. Это и будет примером аппроксимирующей формулы. На нашем сайте вы также можете найти десятки примеров аппроксимации.
Но чтобы получить более или менее содержательное представление, скажем, о пилке дров, надо сначала обрести хотя бы какие-то навыки владения пилой. Тоже самое и с аппроксимацией.
P.S. Решил посмотреть как интерпретируется слово «аппроксимация» в сети интернет. Более других мне понравилась интерпретация в Большом Энциклопедическом Словаре (БЭС):
Только «замена» – это, в моем понимании, нечто вторичное. А первичное – «приближение». Я, например, порой строил десятки аппроксимирующих формул, добиваясь наилучшего приближения к исходной таблице данных. А собственно «замена» в основном касалась замены одной аппроксимирующей формулы на другую, более удачную. Впрочем, пользователь уже мог использовать мою аппроксимирующую формулы «взамен» исходной таблицы.
В Большой Советской Энциклопедии (БСЭ) находим более развернутое определение:
«Аппроксимация (от лат. approximo — приближаюсь), замена одних математических объектов другими, в том или ином смысле близкими к исходным. Аппроксимация позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (например, таких, характеристики которых легко вычисляются или свойства которых уже известны). В теории чисел изучаются диофантовы приближения, в частности приближения иррациональных чисел рациональными. В геометрии и топологии рассматриваются аппроксимации кривых, поверхностей, пространств и отображений. Некоторые разделы математики целиком посвящены аппроксимации; например, приближение и интерполирование функций, численные методы анализа. Роль аппроксимации в математике непрерывно возрастает. В настоящее время аппроксимация может рассматриваться как одно из основных понятий математики». С. Б. Стечкин.
Осталось только поинтересоваться что означают «диофантовы приближения» и прочие специальные термины и все станет окончательно понятно.
В Википедии (свободной энциклопедии) очень короткое определение:
«Аппроксимация, или приближение — научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми».
Позволю себе заметить, что «приближение» – это не есть «замена» или это «замена» в каком-то очень узком и специальном смысле, например в смысле «использование вместо».
В словаре бизнес-терминов находим весьма расплывчатое, на мой взгляд, определение:
«Аппроксимация – приближенное решение сложной функции с помощью более простых, что резко ускоряет и упрощает решение задач. В экономике целью аппроксимации часто является укрупнение характеристик моделируемых экономических объектов».
В философской энциклопедии:
«АППРОКСИМАЦИЯ (от лат. approximare — приближаться) — метод сознательного упрощения «слишком точного» теоретического знания с целью привести его в соответствие с потребностями и возможностями практики. Например, использование числа «пи» с точностью до пятого знака после запятой достаточно для решения поставленной практической задачи. Аппроксимация первоначально использовалась в математике и затем распространилась на все науки. Аппроксимация противоположна идеализации». Г. Д. Левин.
В научной диалектике есть положение: «Истина всегда конкретна». Так и с аппроксимацией – нет аппроксимации «вообще». Ее содержательная часть – в конкретных приложениях и в конкретных областях. Я, например, занимался аппроксимацией графиков и табличных данных посредством подбора подходящих для этого формул с использованием метода наименьших квадратов, встроенного в электронные таблицы Quattro Pro и Excel. А способов подбора – десятки, и это уже не только наука, но и искусство. Ваш, Протасов Н.Г.
Задача аппроксимации (задача о приближении)
Пусть y = f(x) является функцией аргумента х. Нередко эта зависимость задается в табличном виде. В контрольных по математике на аппроксимацию также часто требуется найти некоторую аналитическую функцию, которая приближенно описывает заданную табличную зависимость. Кроме того, требуется определить значения функции в других точках, отличных от заданных табличных значений. Этой цели служит задача о приближении (аппроксимации). В этом случае находят некоторую функцию f(х), такую, чтобы отклонения ее от заданной табличной функции было наименьшим. Функция f(х) называется аппроксимирующей.
Вид аппроксимирующей функции существенным образом зависит от исходной табличной функции. В разных случаях функцию f(х) выбирают в виде экспоненциальной, логарифмической, степенной, синусоидальной и т.д. В каждом конкретном случае выбирают таким образом, чтобы достичь максимальной близости аппроксимирующей и табличной функций. Чаще всего, однако, функцию представляют в виде полинома по степеням х:
Коэффициенты aj подбираются таким образом, чтобы достичь наименьшего отклонения полинома от заданной функции.
Таким образом, аппроксимация – замена одной функции другой, близкой к первой и достаточно просто вычисляемой».
Лично я редко пользуюсь полиномами в их классическом виде, как и другими стандартными представлениями, указанными в статье. Однако это уже нюансы технологии построения аппроксимирующих формул.