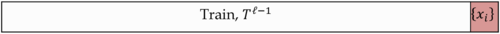Для чего нужна кросс валидация
Кросс-валидация
Кросс-валидация или скользящий контроль — процедура эмпирического оценивания обобщающей способности алгоритмов. С помощью кросс-валидации эмулируется наличие тестовой выборки, которая не участвует в обучении, но для которой известны правильные ответы.
Содержание
Определения и обозначения [ править ]
Пусть [math] X [/math] — множество признаков, описывающих объекты, а [math] Y [/math] — конечное множество меток.
[math]T^l = <(x_i, y_i)>_
[math]Q[/math] — мера качества,
[math]\mu: (X \times Y)^l \to A, [/math] — алгоритм обучения.
Разновидности кросс-валидации [ править ]
Валидация на отложенных данных (Hold-Out Validation) [ править ]
Обучающая выборка один раз случайным образом разбивается на две части [math] T^l = T^t \cup T^
После чего решается задача оптимизации:
Метод Hold-out применяется в случаях больших датасетов, т.к. требует меньше вычислительных мощностей по сравнению с другими методами кросс-валидации. Недостатком метода является то, что оценка существенно зависит от разбиения, тогда как желательно, чтобы она характеризовала только алгоритм обучения.
Полная кросс-валидация (Complete cross-validation) [ править ]
Здесь число разбиений [math]C_l^
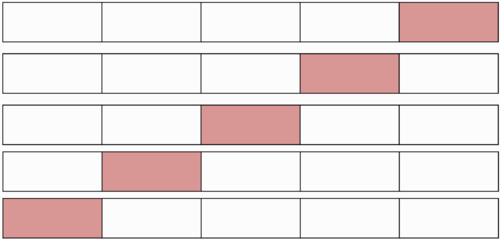
k-fold кросс-валидация [ править ]
Каждая из [math]k[/math] частей единожды используется для тестирования. Как правило, [math]k = 10[/math] (5 в случае малого размера выборки).
t×k-fold кросс-валидация [ править ]
Кросс-валидация по отдельным объектам (Leave-One-Out) [ править ]
Выборка разбивается на [math]l-1[/math] и 1 объект [math]l[/math] раз.
Преимущества LOO в том, что каждый объект ровно один раз участвует в контроле, а длина обучающих подвыборок лишь на единицу меньше длины полной выборки.
Недостатком LOO является большая ресурсоёмкость, так как обучаться приходится [math]L[/math] раз. Некоторые методы обучения позволяют достаточно быстро перенастраивать внутренние параметры алгоритма при замене одного обучающего объекта другим. В этих случаях вычисление LOO удаётся заметно ускорить.
Случайные разбиения (Random subsampling) [ править ]
Выборка разбивается в случайной пропорции. Процедура повторяется несколько раз.
Критерий целостности модели (Model consistency criterion) [ править ]
Не переобученый алгоритм должен показывать одинаковую эффективность на каждой части.
Перекрёстная проверка (кросс-валидация, Cross-validation) — метод оценки аналитической модели и её поведения на независимых данных. При оценке модели имеющиеся в наличии данные разбиваются на k частей. Затем на k−1 частях данных производится обучение модели, а оставшаяся часть данных используется для тестирования. Процедура повторяется k раз; в итоге каждая из k частей данных используется для тестирования. В результате получается оценка эффективности выбранной модели с наиболее равномерным использованием имеющихся данных.
Обычно кросс-валидация используется в ситуациях, где целью является предсказание, и хотелось бы оценить, насколько предсказывающая модель способна работать на практике. Один цикл кросс-валидации включает разбиение набора данных на части, затем построение модели на одной части (называемой тренировочным набором), и валидация модели на другой части (называемой тестовым набором). Чтобы уменьшить разброс результатов, разные циклы кросс-валидации проводятся на разных разбиениях, а результаты валидации усредняются по всем циклам.
Кросс-валидация важна для защиты от гипотез, навязанных данными («ошибки третьего рода»), особенно когда получение дополнительных данных затруднительно или невозможно.
Предположим, у нас есть модель с одним или несколькими неизвестными параметрами, и набор данных, на котором эта модель может быть оптимизирована (тренировочный набор). Процесс подгонки оптимизирует параметры модели и делает модель настолько подходящей под тренировочный набор, насколько это возможно. Если мы теперь возьмем независимый образец данных для валидации модели из того же источника, откуда мы взяли тренировочный набор данных, обычно обнаруживается, что модель описывает тестовые данные хуже, чем тренировочный набор. Это называется переподгонкой (overfitting), и особенно часто встречается в ситуациях, когда размер тренировочного набора невелик, или когда число параметров в модели велико. Кросс-валидация это способ оценить способность модели работать на гипотетическом тестовом наборе, когда такой набор в явном виде получить невозможно.
Распространенные типы кросс-валидации
Кросс-валидация по K блокам (K-fold cross-validation)
В этом случае исходый набор данных разбивается на K одинаковых по размеру блока. Из K блоков один оставляется для тестирования модели, а остающиеся K-1 блока используются как тренировочный набор. Процесс повторяется K раз, и каждый из блоков используется один раз как тестовый набор. Получаются K результатов, по одному на каждый блок, они усредняются или комбинируются каким-либо другим способом, и дают одну оценку. Преимущество такого способа перед случайным сэмплированием (random subsampling) в том, что все наблюдения используются и для тренировки, и для тестирования модели, и каждое наблюдение используется для тестирования в точности один раз. Часто используется кросс-валидация на 10 блоках, но каких-то определенных рекомендаций по выбору числа блоков нет.
В послойной кросс-валидации блоки выбираются таким образом, что среднее значение ответа модели примерно равно по всем блокам.
Валидация последовательным случайным сэмплированием (random subsampling)
Этот метод случайным образом разбивает набор данных на тренировочный и тестовый наборы. Для каждого такого разбиения, модель подгоняется под тренировочные данные, а точность предсказания оценивается на тестовом наборе. Результаты затем усредняются по всем разбиениям. Преимущество такого метода перед кросс-валидацией на K блоках в том, что пропорции тренировочного и тестового наборов не зависят от числа повторений (блоков). Недостаток метода в том, что некоторые наблюдения могут ни разу не попасть в тестовый набор, тогда как другие могут попасть в него более, чем один раз. Другими словами, тестовые наборы могут перекрываться. Кроме того, поскольку разбиения проводятся случайно, результаты будут отличаться в случае повторного анализа.
В послойном варианте этого метода, случайные выборки генерируются таким способом, при котором средний ответ модели равен по тренировочному и тестовому наборам. Это особенно полезно, когда ответ модели бинарен, с неравными пропорциями ответов по данным.
Поэлементная кросс-валидация (Leave-one-out, LOO)
Здесь отдельное наблюдение используется в качестве тестового набора данных, а остальные наблюдения из исходного набора – в качестве тренировочного. Цикл повторяется, пока каждое наблюдение не будет использовано один раз в качестве тестового. Это то же самое, что и K-блочная кросс-валидация, где K равно числу наблюдений в исходном наборе данных.
Оценка соответствия модели
Цель кросс-валидации в том, чтобы оценить ожидаемый уровень соответствия модели данным, независимым от тех данных, на которых модель тренировалась. Она может использоваться для оценки любой количественной меры соответствия, подходящей для данных и модели. Например, для задачи бинарной классификации, каждый случай в тестовом наборе будет предсказан правильно или неправильно. В этой ситуации коэффициент ошибки может быть использован в качестве оценки соответствия, хотя могут использоваться и другие оценки. Если предсказываемое значение распределено непрерывно, для оценки соответствия может использоваться среднеквадратичная ошибка, корень из среднеквадратичной ошибки или медианное абсолютное отклонение.
Применения кросс-валидации
Кросс-валидация может использоваться для сравнения результатов различных процедур предсказывающего моделирования. Например, предположим, что мы интересуемся оптическим распознаванием символов, и рассматриваем варианты использования либо поддерживающих векторов (Support Vector Machines, SVM), либо k ближайших соседей (k nearest neighbors, KNN). С помощью кросс-валидации мы могли бы объективно сравнить эти два метода в терминах относительных коэффициентов их ошибок классификаций. Если мы будем просто сравнивать эти методы по их ошибкам на тренировочной выборке, KNN скорее всего покажет себя лучше, поскольку он более гибок и следовательно более склонен к переподгонке по сравнению с SVM.
Кросс-валидация также может использоваться для выбора параметров. Предположим, у нас есть 20 параметров, которые мы могли бы использовать в модели. Задача – выбрать параметры, использование которых даст модель с лучшими предсказывающими способностями. Если мы будем сравнивать подмножества параметров по их ошибкам на тестовом наборе, лучшие результаты получатся при использовании всех параметров. Однако с кросс-валидацией, модель с лучшей способностью к обобщению обычно включает только некоторое подмножество параметров, которые достаточно информативны.
Вопросы вычислительной производительности
Ограничения и неверное использование кросс-валидации
Кросс-валидация дает значимые результаты только когда тренировочный набор данных и тестовый набор данных берутся из одного источника, из одной популяции. В многих применениях предсказательных моделей структура изучаемой системы меняется со временем. Это может наводить систематические отклонения тренировочного и валидационного наборов данных. К примеру, если модель для предсказания цены акции тренируется на данных из определенного пятилетнего периода, нереалистично рассматривать последующий пятилетний период как выборку из той же самой популяции.
Если выполняется правильно, и наборы данных из одной популяции, кросс-валидация дает результат практически без смещений (bias). Однако, есть много способов использовать кросс-валидацию неправильно. В этом случае ошибка предсказания на реальном валидационном наборе данных скорее всего будет намного хуже, чем ожидается по результатам кросс-валидации.
Способы неверно использовать кросс-валидацию:
1. Использовать кросс-валидацию на нескольких моделях, и взять только результаты лучшей модели.
2. Проводить начальный анализ для определения наиболее информативного набора параметров, используя полный набор данных. Если отбор параметров требуется в модели предсказания, он должен проводиться последовательно на каждом тренировочном наборе данных. Если кросс-валидация используется для определения набора используемых моделью параметров, на каждом тренировочном наборе должна проводиться внутренняя кросс-валидация для определения набора параметров.
3. Позволять некоторым тренировочным данным попадать также и в тестовый набор – это может случиться из-за существования дублирующих наблюдений в исходном наборе.
Кросс-валидация (Cross Validation)
Кросс-валидация (перекрестная проверка) – это метод оценки Моделей (Model) Машинного обучения (ML) путем обучения нескольких из них на подмножествах доступных входных данных и их оценки на другом дополнительном подмножестве. Такая проверка используется для обнаружения Переобучения (Overfitting), т.е. неспособности распознать паттерн.
Всегда необходимо проверять стабильность предсказывающего Алгоритма (Algorithm): нам нужна уверенность в том, что модель имеет представление о большинстве шаблонов в данных, что ее эффективность не падает от шумных данных, или, другими словами, у нее низкий уровень Смещения (Bias) и Дисперсии (Variance).
Проверка
Валидация – это процесс принятия решения о том, приемлемы ли числовые результаты, определяющие предполагаемые взаимосвязи между переменными в качестве характеристики данных. Как правило, оценка Ошибки (Error) для модели выполняется после обучения, более известного как оценка Остатков (Residuals). Мы выполняем численную оценка ошибкой обучения – разницы в предсказанных и истинных ответах. Однако это только дает нам представление о том, насколько хорошо модель работает с Тренировочными данными (Train Data). Однако вероятно, что модель склонна к переобучению или Недообучению (Underfitting). Проблема этого метода оценки заключается в том, что он не гарантирует приемлемый уровень обобщения новых неизвестных данных.
Метод удержания (Holdout Method)
Простое решение вышеописанной проблемы заключается в удержании части обучающих данных и использовании ее для оценки предсказательной способности. Ошибка сообщает затем, как наша модель работает с новыми данными или валидационным набором. Хотя этот метод не требует дополнительных вычислительных затрат и лучше, чем традиционная проверка, он все же подвержен высокой дисперсии. Неизвестно, какие точки данных попадут в набор для проверки, и результат может быть совершенно разным для каждой случайной Выборки (Sample).
Кросс-валидация по K блокам
Поскольку все возможные варианты загрузить в модель непросто, удержание части Датасета (Dataset) для проверки создает проблему недообучения. Уменьшая объем обучающих данных, мы рискуем потерять важные закономерности и тенденции в наборе, что, в свою очередь, увеличивает ошибку, вызванную смещением. Итак, нам нужен метод, который предоставляет достаточно данных для обучения модели, а также оставляет достаточно данных для проверки. Кросс-валидация по K блокам (K-Fold Cross Vaidation) делает именно это.
При K-Fold проверке данные делятся на k подмножеств. Теперь удержание повторяется k раз, так что каждый из k подмножеств используется в качестве проверочного набора, а другие подмножества k-1 объединяются, чтобы сформировать обучающий набор. Ошибка усредняется по всем k испытаниям, чтобы получить обощенную эффективность нашей модели. Каждая точка данных попадает в набор для проверки ровно один раз и попадает в обучающий набор k-1 раз. Это значительно снижает смещение, поскольку мы используем большую часть данных для подгонки, а также значительно сокращаем дисперсию, поскольку большая часть данных также используется в наборе для проверки. Перестановка тренировочного и тестового наборов также повышает эффективность этого метода. По умолчанию K равен 5 или 10, но может принимать и любое другое значение.
Стратифицированная кросс-валидация по K блокам
В некоторых случаях может быть большой естественный дисбаланс. Например, в датасете о ценах на недвижимость может быть большое количество домов с высокой ценой. Или в случае Классификации (Classification), представителей одного класса может быть в несколько раз больше, чем другого. Для таких ситуаций и делается небольшое изменение в методике перекрестной проверки, так что каждый блок содержит примерно такую же пропорцию классов. Этот вариант проверки также известен как стратифицированная кросс-валидация по K блокам.
Вышеупомянутые методы называют неисчерпывающими методами перекрестной проверки. Они не вычисляют все способы разделения исходной выборки, т.е. вам просто нужно решить, сколько подмножеств необходимо сделать. Кроме того, это приближения метода, описанного ниже, также называемого исчерпывающим методом, который вычисляет все возможные способы разделения данных на обучающие и тестовые наборы.
Перекрестная проверка без исключения
Leave-P-Out Cross Validation (LPO) оставляет P точек данных за пределами обучающего набора, т.е. если в исходной выборке имеется N точек данных, тогда N-P выборок используются для обучения модели, а P точек используются в качестве набора для проверки. Это повторяется для всех комбинаций, в которых исходный образец может быть отделен таким образом, а затем ошибка усредняется для всех испытаний, чтобы оценить общую эффективность.
Этот метод является исчерпывающим в том смысле, что он должен обучать и проверять модель для всех возможных комбинаций, а для умеренно больших P он может стать вычислительно невыполнимым.
Частным случаем этого метода является P = 1. Он известен как Поэлементная кросс-валидация (LOO). Этот метод предпочтительнее предыдущего, потому что не страдает от массивных вычислений, и количество возможных комбинаций равно количеству точек данных в исходной выборке (N).
Перекрестная проверка – очень полезный метод оценки эффективности вашей модели, особенно в тех случаях, когда вам нужно уменьшить переобучение. Это также полезно при определении Гиперпараметров (Hyperparameter) при поиске наименьшей ошибки.
Кросс-валидация и Scikit-learn
Давайте посмотрим, как кросс-валидация реализована в SkLearn. Для начала импортируем необходимые библиотеки:
Используем датасет о пациентах, у которых диагностируют диабет. Отделим Предикторы (Predictor Variable) от Целевой переменной (Target Variable), создав объекты X и y соответственно. Для совершенствования модели используем так называемую Регуляризацию Лассо (L1 Regularization):
Отсортированный от большего к меньшему список точностей выглядит весьма плачевно: линейная модель справилась лишь с 33% наблюдений:
Ну что ж, модель учебная, так что низкая предсказательная способность здесь не главное, хоть результат и улучшился до 39%. Процесс совершенствования модели здесь только начинается, и MSE каждой итерации – прекрасный способ сравнивать между собой качество последующих апгрейдов:
Ноутбук, не требующий дополнительной настройки на момент написания статьи, можно скачать здесь.
Автор оригинальной статьи: @prashantgupta17
3.1. Перекрестная проверка: оценка производительности ¶
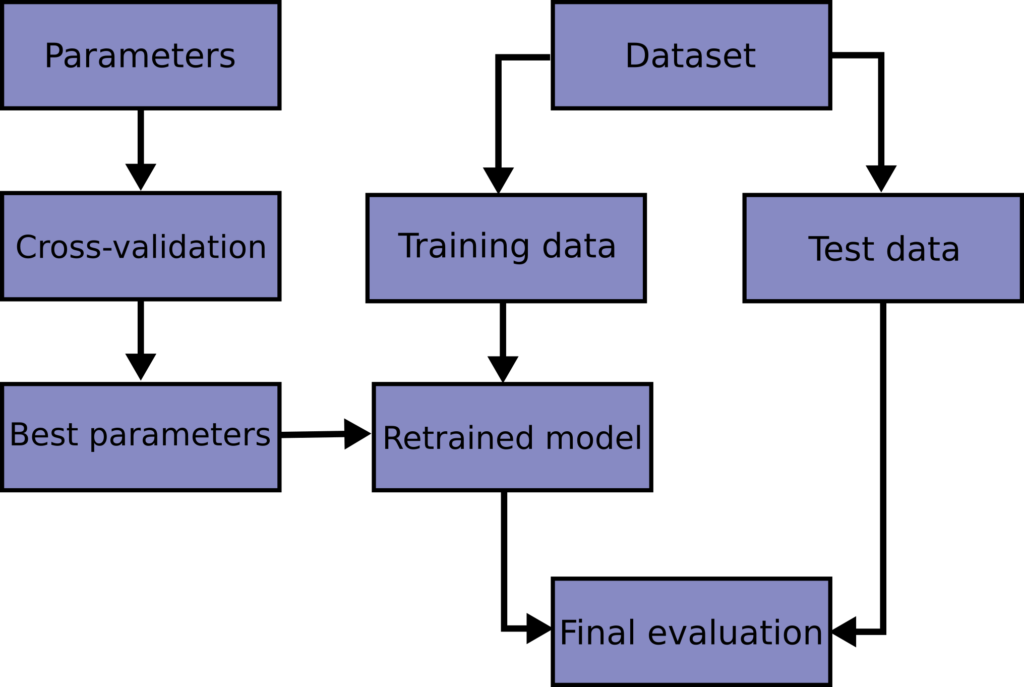
Изучение параметров функции прогнозирования и тестирование ее на одних и тех же данных является методологической ошибкой: модель, которая будет просто повторять метки образцов, которые она только что увидела, будет иметь идеальную оценку, но пока не сможет предсказать что-либо полезное. невидимые данные. Такая ситуация называется переобучением. Чтобы этого избежать, при проведении (контролируемого) эксперимента с машинным обучением обычно используется часть имеющихся данных в виде набора тестов X_test, y_test. Обратите внимание, что слово «эксперимент» не предназначено для обозначения только академического использования, потому что даже в коммерческих условиях машинное обучение обычно начинается экспериментально. Вот блок-схема типичного рабочего процесса перекрестной проверки при обучении модели. Лучшие параметры могут быть определены методами поиска по сетке.
В scikit-learn можно быстро вычислить случайное разбиение на обучающие и тестовые наборы с помощью train_test_split вспомогательной функции. Давайте загрузим набор данных диафрагмы, чтобы он соответствовал линейной машине опорных векторов:
Теперь мы можем быстро выбрать обучающий набор, сохраняя 40% данных для тестирования (оценки) нашего классификатора:
Однако, разбивая доступные данные на три набора, мы резко сокращаем количество выборок, которые можно использовать для обучения модели, а результаты могут зависеть от конкретного случайного выбора для пары наборов (обучение, проверка).
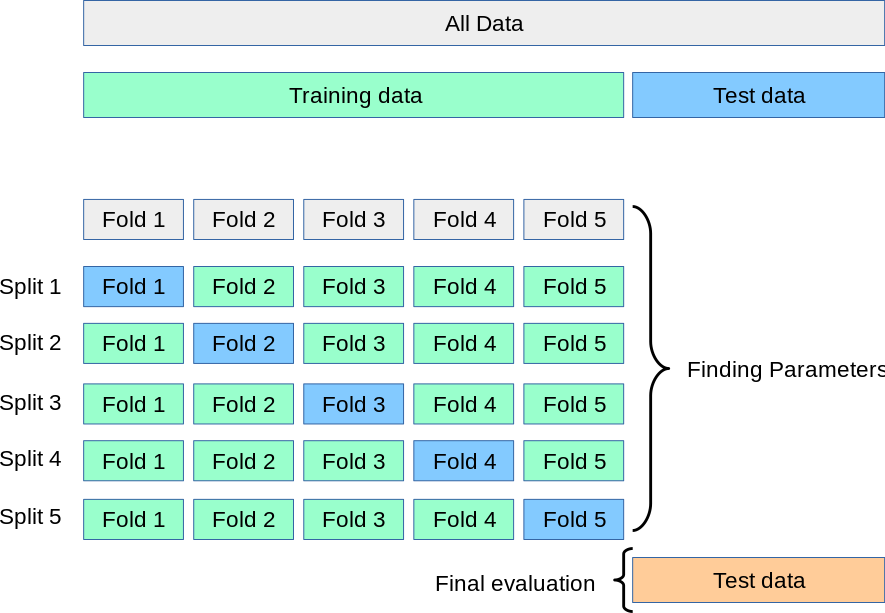
Решением этой проблемы является процедура перекрестной проверки (cross-validation сокращенно CV). Набор тестов по-прежнему должен храниться для окончательной оценки, но набор для проверки больше не нужен при выполнении резюме. В базовом подходе, называемом k- кратным CV, обучающая выборка разбивается на k меньших наборов (другие подходы описаны ниже, но обычно следуют тем же принципам). Для каждой из k «фолдов» выполняется следующая процедура :
Показатель производительности, сообщаемый k- фолд перекрестной проверкой, тогда является средним из значений, вычисленных в цикле. Этот подход может быть дорогостоящим в вычислительном отношении, но не тратит слишком много данных (как в случае фиксации произвольного набора проверки), что является основным преимуществом в таких задачах, как обратный вывод, когда количество выборок очень мало.
3.1.1. Вычисление метрик с перекрестной проверкой
Самый простой способ использовать перекрестную проверку — вызвать cross_val_score вспомогательную функцию для оценщика и набора данных.
В следующем примере показано, как оценить точность машины вектора поддержки линейного ядра в наборе данных радужной оболочки путем разделения данных, подбора модели и вычисления оценки 5 раз подряд (с разными разбиениями каждый раз):
Таким образом, средний балл и стандартное отклонение выражаются следующим образом:
По умолчанию оценка, вычисляемая на каждой итерации CV, является score методом оценщика. Это можно изменить, используя параметр оценки:
Также можно использовать другие стратегии перекрестной проверки, передав вместо этого итератор перекрестной проверки, например:
Другой вариант — использовать итерируемые разбиения с получением (train, test) как массивы индексов, например:
Преобразование данных с сохраненными данными
Подобно тому, как важно протестировать предсказатель на данных, полученных в результате обучения, предварительная обработка (например, стандартизация, выбор функций и т. Д.) И аналогичные преобразования данных аналогичным образом должны быть изучены из обучающего набора и применены к удерживаемым данным для прогнозирования. :
A Pipeline упрощает составление оценщиков, обеспечивая такое поведение при перекрестной проверке:
3.1.1.1. Функция cross_validate и оценка нескольких показателей
В cross_validate функции отличается от cross_val_score двух способов:
Для оценки единственной метрики, где параметром скоринга является строка, вызываемая или None, ключи будут: [‘test_score’, ‘fit_time’, ‘score_time’]
А для оценки нескольких показателей возвращаемое значение — это dict со следующими ключами: [‘test_ ‘, ‘test_ ‘, ‘test_ ‘, ‘fit_time’, ‘score_time’]
Множественные показатели могут быть указаны в виде списка, кортежа или набора заранее определенных имен счетчиков:
Или как dict сопоставление имени счетчика с предопределенной или настраиваемой функцией оценки:
Вот пример cross_validate использования одной метрики:
3.1.1.2. Получение прогнозов путем перекрестной проверки
Замечание о неправильном использовании cross_val_predict. Результат cross_val_predict может отличаться от полученного при использовании, cross_val_score поскольку элементы сгруппированы по-разному. Функция cross_val_score берет среднее значение по сверткам перекрестной проверки, тогда как cross_val_predict просто возвращает метки (или вероятности) из нескольких различных моделей без различия. Таким образом, cross_val_predict не является подходящей мерой ошибки обобщения.
Доступные итераторы перекрестной проверки представлены в следующем разделе.
3.1.2. Итераторы перекрестной проверки
В следующих разделах перечислены утилиты для создания индексов, которые можно использовать для создания разбиений наборов данных в соответствии с различными стратегиями перекрестной проверки.
3.1.2.1. Итераторы перекрестной проверки для данных
Предполагая, что некоторые данные являются независимыми и идентично распределенными (Independent and Identically Distributed — i.i.d.), предполагается, что все выборки происходят из одного и того же генерирующего процесса и что генеративный процесс не имеет памяти о сгенерированных ранее выборках.
В таких случаях можно использовать следующие кросс-валидаторы.
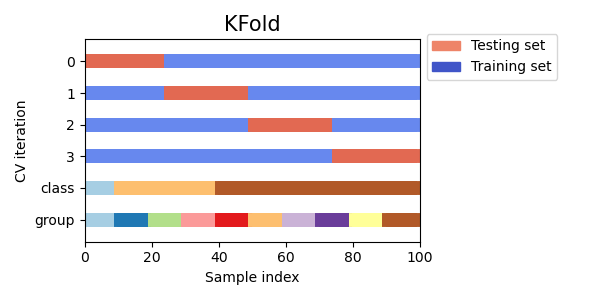
3.1.2.1.1. K-фолд
Пример 2-фолдовой перекрестной проверки на наборе данных с 4 образцами:
Вот визуализация поведения перекрестной проверки. Обратите внимание, на KFold не влияют классы или группы.
3.1.2.1.2. Повторяющийся K-Fold
RepeatedKFold повторяет K-Fold n раз. Его можно использовать, когда нужно выполнить KFold n раз, производя разные разбиения в каждом повторении.
Пример 2-кратного K-Fold повторяется 2 раза:
Аналогичным образом, RepeatedStratifiedKFold повторяет стратифицированный K-Fold n раз с различной рандомизацией в каждом повторении.
3.1.2.1.3. Оставьте один вне (LOO)
Пример Leave-2-Out в наборе данных с 4 образцами:
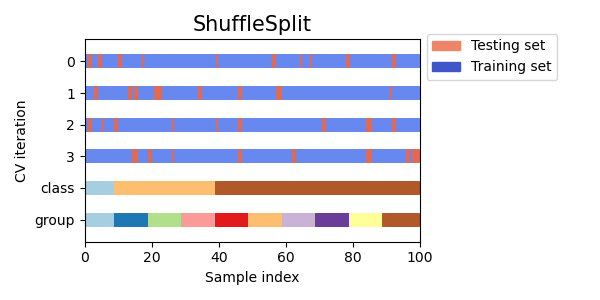
3.1.2.1.5. Перекрестная проверка случайных перестановок, известная как Shuffle & Split
Итератор ShuffleSplit будет генерировать, определенные пользователем, число независимых обученые / тестовые наборы данных разделений. Образцы сначала перемешиваются, а затем разделяются на пару наборов для обучения и тестов.
Можно контролировать случайность для воспроизводимости результатов путем явного заполнения random_state генератора псевдослучайных чисел.
Вот пример использования:
Вот визуализация поведения перекрестной проверки. Обратите внимание, на ShuffleSplit это не влияют классы или группы.
Таким образом ShuffleSplit это хорошая альтернатива KFold перекрестной проверке, которая позволяет более точно контролировать количество итераций и долю выборок на каждой стороне разделения обучения / тест.
3.1.2.2. Итераторы перекрестной проверки со стратификацией на основе меток классов.
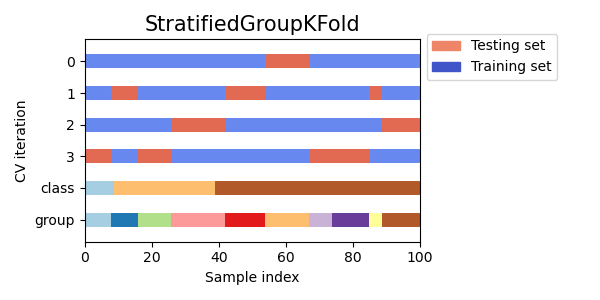
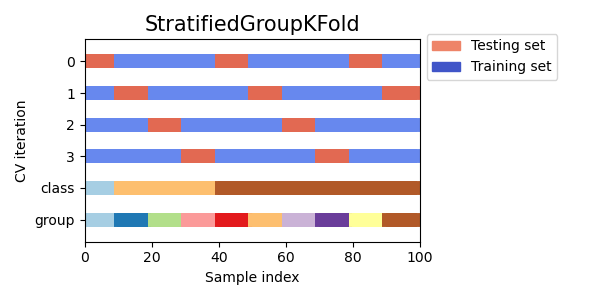
Некоторые проблемы классификации могут демонстрировать большой дисбаланс в распределении целевых классов: например, отрицательных образцов может быть в несколько раз больше, чем положительных. В таких случаях рекомендуется использовать стратифицированную выборку, как это реализовано в, StratifiedKFold и StratifiedShuffleSplit гарантировать, что относительная частота классов приблизительно сохраняется в каждой последовательности и валидации.
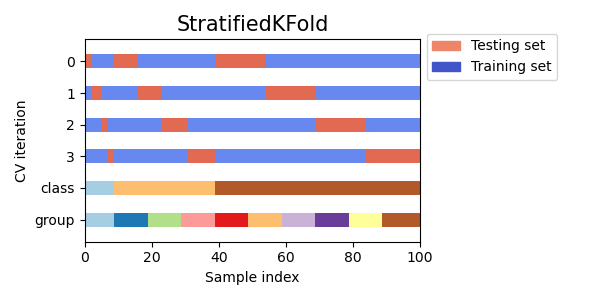
3.1.2.2.1. Стратифицированный k-фолд
StratifiedKFold представляет собой разновидность k-фолдовой кратности, которая возвращает стратифицированные фолды: каждый набор содержит примерно такой же процент выборок каждого целевого класса, что и полный набор.
Мы видим, что StratifiedKFold соотношение классов (примерно 1/10) сохраняется как в обучающем, так и в тестовом наборе данных.
Вот визуализация поведения перекрестной проверки.
RepeatedStratifiedKFold может использоваться для повторения стратифицированного K-фолдов n раз с различной рандомизацией в каждом повторении.
3.1.2.2.2. Стратифицированное перемешивание в случайном порядке
Вот визуализация поведения перекрестной проверки.
3.1.2.3. Итераторы перекрестной проверки для сгруппированных данных.
Предположение iid нарушается, если основной процесс генерации дает группы зависимых выборок.
Такая группировка данных зависит от предметной области. В качестве примера можно привести медицинские данные, собранные у нескольких пациентов, с множеством образцов, взятых у каждого пациента. И такие данные, вероятно, будут зависеть от отдельной группы. В нашем примере идентификатор пациента для каждого образца будет идентификатором его группы.
В этом случае мы хотели бы знать, хорошо ли модель, обученная на конкретном наборе групп, обобщается на невидимые группы. Чтобы измерить это, нам нужно убедиться, что все выборки в фолдовой проверке взяты из групп, которые вообще не представлены в парной обучающей выборке.
Для этого можно использовать следующие разделители перекрестной проверки. Идентификатор группировки для образцов указывается через groups параметр.
3.1.2.3.1. Группа K фолд
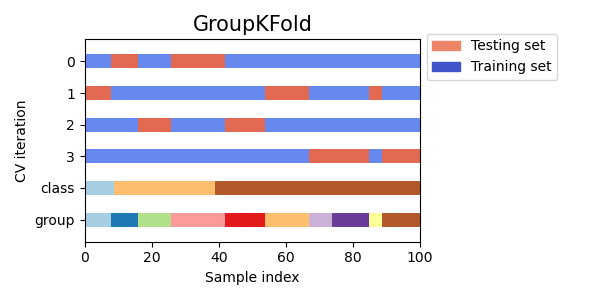
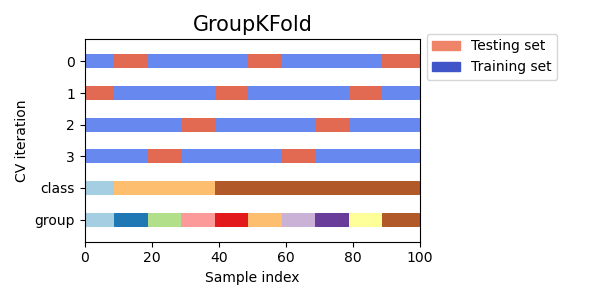
GroupKFold представляет собой вариант k-фолдовое увеличение, которое гарантирует, что одна и та же группа не будет представлена как в тестовой, так и в обучающей выборке. Например, если данные получены от разных субъектов с несколькими выборками по каждому субъекту, и если модель достаточно гибкая, чтобы учиться на личностно-специфических особенностях, ее нельзя будет обобщить на новые темы. GroupKFold п озволяет обнаруживать такого рода ситуации переобучения.
Представьте, что у вас есть три предмета, каждому из которых соответствует номер от 1 до 3:
Каждый предмет проходит разные этапы тестирования, и один и тот же предмет никогда не проходит и в тестировании, и в обучении. Обратите внимание, что складки не имеют точно такого же размера из-за несбалансированности данных.
Вот визуализация поведения перекрестной проверки.
3.1.2.3.2. Оставьте одну группу вне (Leave One Group Out)
LeaveOneGroupOut представляет собой схему перекрестной проверки, в которой образцы хранятся в соответствии с массивом целочисленных групп, предоставленным третьей стороной. Эту групповую информацию можно использовать для кодирования произвольных предопределенных фолдов перекрестной проверки, зависящих от домена.
Таким образом, каждый обучающий набор состоит из всех выборок, кроме тех, которые относятся к определенной группе.
Например, в случаях нескольких экспериментов, LeaveOneGroupOut может использоваться для создания перекрестной проверки на основе различных экспериментов: мы создаем обучающий набор, используя образцы всех экспериментов, кроме одного:
Другое распространенное применение — использование информации о времени: например, группы могут быть годом сбора образцов и, таким образом, допускать перекрестную проверку на разбиение по времени.
3.1.2.3.3. Оставьте P групп вне (Leave P Groups Out)
Пример выхода из группы 2 из 2:
3.1.2.3.4. Групповой случайный сплит
Вот пример использования:
Вот визуализация поведения перекрестной проверки.
3.1.2.4. Предопределенные Fold-Splits / Validation-Sets
Для некоторых наборов данных уже существует предварительно определенное разделение данных на фолды обучения и теста или на несколько фолдов перекрестной проверки. С PredefinedSplit помощью этих фолдов можно использовать, например, при поиске гиперпараметров.
3.1.2.5. Использование итераторов перекрестной проверки для разделения обучения и тестирования
Вышеупомянутые групповые функции перекрестной проверки также могут быть полезны для разделения набора данных на подмножества обучения и тестирования. Обратите внимание, что вспомогательная функция train_test_split является оболочкой ShuffleSplit и, таким образом, допускает только стратифицированное разбиение (с использованием меток классов) и не может учитывать группы.
Чтобы выполнить разделение поезда и теста, используйте индексы для подмножеств поезда и теста, полученные на выходе генератора split() методом разделителя перекрестной проверки. Например:
3.1.2.6. Перекрестная проверка данных временных рядов
3.1.2.6.1. Разделение временных рядов
TimeSeriesSplit это вариант k-фолд возврата, который возвращается первымk складывается как набор поездов и ($k+1$)-я фолдов в качестве тестового набора. Обратите внимание, что в отличие от стандартных методов перекрестной проверки, последовательные обучающие наборы являются надмножествами предшествующих. Кроме того, он добавляет все лишние данные в первый обучающий раздел, который всегда используется для обучения модели.
Этот класс можно использовать для перекрестной проверки выборок данных временных рядов, которые наблюдаются через фиксированные интервалы времени.
Пример перекрестной проверки 3-сегментных временных рядов на наборе данных с 6 выборками:
Вот визуализация поведения перекрестной проверки.
3.1.3. Замечание о перемешивании
Если порядок данных не является произвольным (например, выборки с одной и той же меткой класса являются смежными), сначала перетасовка данных может быть существенной для получения значимого результата перекрестной проверки. Однако может быть и обратное, если образцы не распределены независимо и одинаково. Например, если образцы соответствуют новостным статьям и упорядочены по времени публикации, то перетасовка данных, скорее всего, приведет к переобучению модели и завышенной оценке валидации: она будет проверена на образцах, которые искусственно похожи (близкие вовремя) к обучающим выборкам.
3.1.4. Перекрестная проверка и выбор модели
3.1.5. Результат теста на перестановку (Permutation test score)
permutation_test_score предлагает другой способ оценки производительности классификаторов. Он обеспечивает p-значение на основе перестановок, которое показывает, насколько вероятно, что наблюдаемая производительность классификатора будет получена случайно. Нулевая гипотеза в этом тесте заключается в том, что классификатор не может использовать какую-либо статистическую зависимость между функциями и метками, чтобы делать правильные прогнозы на основе оставленных данных. permutation_test_score генерирует нулевое распределение, вычисляя n_permutations различные перестановки данных. В каждой перестановке метки случайным образом перемешиваются, тем самым удаляя любую зависимость между функциями и метками. Выходное значение p — это доля перестановок, для которых средняя оценка перекрестной проверки, полученная моделью, лучше, чем оценка перекрестной проверки, полученная моделью с использованием исходных данных. Для надежных результатов n_permutations обычно должно быть больше 100 и составлять cv от 3 до 10 фолдов.
Низкое значение p свидетельствует о том, что набор данных содержит реальную зависимость между функциями и метками, и классификатор смог использовать это для получения хороших результатов. Высокое значение p могло быть связано с отсутствием зависимости между функциями и метками (нет разницы в значениях функций между классами) или потому, что классификатор не смог использовать зависимость в данных. В последнем случае использование более подходящего классификатора, способного использовать структуру данных, приведет к низкому значению p (p-value).
Перекрестная проверка предоставляет информацию о том, насколько хорошо классификатор обобщает, в частности, о диапазоне ожидаемых ошибок классификатора. Однако классификатор, обученный на многомерном наборе данных без структуры, может работать лучше, чем ожидалось при перекрестной проверке, просто случайно. Обычно это может происходить с небольшими наборами данных, содержащими менее нескольких сотен образцов. permutation_test_score предоставляет информацию о том, нашел ли классификатор реальную структуру классов, и может помочь в оценке производительности классификатора.
Важно отметить, что этот тест показал низкие p-значения, даже если в данных есть только слабая структура, потому что в соответствующих переставленных наборах данных нет абсолютно никакой структуры. Таким образом, этот тест может показать, только когда модель надежно превосходит случайное предположение.
Наконец, permutation_test_score вычисляется методом грубой силы и полностью соответствует (n_permutations + 1) * n_cv моделям. Следовательно, его можно обрабатывать только с небольшими наборами данных, для которых подгонка отдельной модели выполняется очень быстро.