Для чего нужна математическая модель
Просто о сложном: что такое математическое моделирование и почему нам больше не нужны эксперименты на людях
tany_savelieva
Сегодня математики пытаются помочь медикам представить, как устроены внутренние процессы в организме, или предсказать реакцию конкретного пациента на лечение с помощью языков программирования и без проведения дорогих и опасных экспериментов. Метод математического моделирования применяется в самых разных областях науки, в том числе в физиологии и медицине. В рамках проекта «Физтех.Читалка» молодой ученый, аспирант МФТИ Тимур Гамилов рассказал «Теориям и практикам», как математические модели помогают врачам ставить диагнозы, а спортсменам — рекорды.
«Лего» для ученых
Математическое моделирование начали использовать в спорте и медицине еще в 50-х годах. В этой сфере активно работают математики, информатики и физики различных специализаций. Метод математического моделирования устроен по принципу конструктора «Лего», в котором вместо деталей — данные о состоянии здоровья человека и математические формулы, на основе которых врачи ставят диагноз и составляют план лечения. Используя данные о медицинских показателях, математики и инженеры создают гипотезу, которую затем проектируют и проверяют с помощью специального языка программирования.
Неудивительно, что интерес к математическому моделированию в медицине и спорте растет: в США с 1961 по 2006 год процент бюджетных денег, которые тратятся на медицину, возрос с 4% до 20%. В других странах люди тоже хотят жить долго и хорошо, а готовность властей финансировать науку и текущий уровень развития технологий растут с каждым годом. Поэтому вместо того, чтобы проводить медицинские эксперименты на людях, в качестве подопытных кроликов ученые используют математические модели.
Модель для сборки: инструкция
Для построения любой математической модели необходимы данные. Базовые знания о строении и функционировании организма человека можно найти в анатомических атласах и другой справочной литературе. Но поскольку организм каждого человека уникален, врачи наблюдают за каждым пациентом индивидуально: проводят МРТ, компьютерную томографию, измеряют пульс, давление.
Представим, что перед командой ученых (биологов, математиков, физиков, программистов) стоит задача — помочь в постановке диагноза и поиске метода лечения пациентов со стенозом. Первым делом мы, ученые, должны понять, что такое стеноз, и расспрашиваем об этом врачей. Оказывается, стеноз — это возникновение бляшек на сосудах, которые создают разницу в давлении между участками сосуда. В результате сосуд может не выдержать такой нагрузки и порваться. Диагностируется заболевание двумя путями. Первый — качественный способ: нужно сделать снимок сосуда, найти бляшку и по ее виду сделать вывод. Второй — количественный: через бедренную артерию в нужные участки сосуда вводятся датчики, которые измеряют разницу давлений. Результаты количественного анализа — более точные. Это значит, что можно не оперировать пациента без надобности, а осложнения после лечения будут минимальными. Минусы этого способа — в цене и высоких рисках для пациента. Нужна дешевая и безопасная альтернатива, которая поможет поставить количественный диагноз и принять верное решение о лечении. Такой альтернативой может стать математическая модель процессов, происходящих в организме, связанных с развитием болезни.
В нашем случае нужно понять, по каким законам возникает разница в давлениях внутри сосудов, и записать эти законы в виде уравнений. Модели создаются под каждую проблему, болезнь или задачу. Для начала в уравнения (например, гидродинамики) вписывают величины, примерно одинаковые для всех пациентов — в науке они называются константами. Помимо констант, существуют параметры — показатели, которые учитываются для каждого человека индивидуально: длина, ширина сосудов, частота пульса, вид шума в сосудах. После того как мы вписали в уравнения константы, снимаем данные с пациента и записываем их в уравнения. Так ученые связывают параметры и константы с помощью формул: теперь в готовое уравнение мы подставляем разные значения для разных пациентов, чтобы получить необходимый результат — показатель разницы давлений между участками сосуда. Лечение стеноза, в зависимости от степени тяжести заболевания, врачи проводят либо медикаментозно (когда разница в давлениях небольшая), либо с помощью хирургического вмешательства (для более серьезных случаев).
После того как модель запрограммирована, работа не заканчивается. Во-первых, измерить большую часть параметров, которые нужно внести в уравнения, скорее всего, не получится без огромных затрат и дорогостоящих операций. Например, для детального определения структуры бляшек, упругих свойств сосуда и законов, по которым он меняется со временем, потребуется колоссальное количество сил и средств. Поставить такую технологию на поток вряд ли удастся.
Во-вторых, снятые параметры могут измениться через определенное время. Эластичность сосудов сильно меняется в зависимости от гормонов, которые на данный момент присутствуют в крови. А чтобы предсказать, сколько каких гормонов содержится в кровяном русле в интересующий нас период, нужно замоделировать в буквальном смысле весь организм человека, так как гормональный фон зависит от огромного количества факторов.
Врачи не знают математику, а математики — биологию, однако без диалога невозможна ни одна дисциплина на стыке наук
В-третьих, даже если мы сможем измерить все необходимые параметры и они не станут сильно меняться со временем, измерения, скорее всего, будут неточными. И чем больше параметров мы снимаем, тем активнее будет расти эта неточность. А поскольку в организме от небольшого изменения каждого параметра существенно меняются все остальные величины, такая неточность часто становится критичной. Например, даже несущественное количество введенного лекарства, растворяющего тромбы, может привести к передозировке, которая вызовет серьезное кровотечение.
Решаются эти проблемы путем упрощения модели: ученые по максимуму сокращают количество параметров и уравнений, стараются сделать их проще, или, как говорят математики, оптимизируют систему. Несмотря на технологическое несовершенство, метод математического моделирования уже работает и помогает людям. Благодаря математическому моделированию была создана известная модель токов в клетке Ходжкина — Хаксли, которая помогла описать, как распространяются электрохимические импульсы, передающие информацию в организме по нервным клеткам. Эта разработка считается одним из самых важных открытий неврологии XX века. За нее ученые получили Нобелевскую премию.
В помощь Усэйну Болту
Математически смоделированные стратегии для тренировок — уже рутина для спортивной индустрии. Показатели великого бегуна Усэйна Болта почти совпадают с графиком кривой оптимального темпа для бега на 100 метров в каждый момент времени. На соревнованиях по прыжкам с трамплина на лыжах высота конструкции выбирается с использованием математической модели тел спортсменов так, чтобы нагрузки не стали критичны для организма.
Математика + медицина
Главная трудность в развитии метода пока заключается в том, что значительное количество разработок так и остаются теорией. В повседневное клиническое использование вводится крайне малая часть таких проектов. Ученые видят будущее моделей в их адаптации под реальные условия. Теоретические расчеты нужны и важны для понимания процессов, которые происходят в организме, но не менее важно научиться использовать такие расчеты глобально. Сильно упростит задачу, если пациентам будет легко и понятно снимать показатели самостоятельно.
Ученым из разных областей придется все чаще работать на стыке наук и сотрудничать с инженерами и врачами. Чтобы эти идеи не оставались на страницах научных журналов, а реально помогали людям, математики должны начать взаимодействовать с врачами, которые ставят перед ними конкретные медицинские задачи. Такое взаимодействие (из-за особенностей образования и способа мышления) часто дается обеим сторонам непросто: врачи не знают математику, а математики — биологию, все они пользуются разной терминологией и методами. Однако без подобного диалога невозможна ни одна дисциплина на стыке наук.
Математическая модель
Что такое математическая модель
Математическая модель — концепция представления реальности математическим способом, вариант схемы как комплекса, изучение которого позволяет человеку обрести знания о некой другой системе.
Простой пример: график зависимости среднесуточной температуры от времени.
Математическая модель также была создана для того, чтобы проанализировать и предугадать поведение материального объекта. Однако у математической модели есть проблема, от которой не избавиться — идеализация.
Математическое моделирование — процесс создания, а также приемы построения и исследования математических моделей.
Все науки, которые используют для решения своих задач математический аппарат, практикуют математическое моделирование. То есть, заменяют объект своего исследования математической моделью и занимаются исследованием последней.
При помощи совокупности математических методов можно описать образцовый объект или процесс, который построен на стадии содержательного моделирования.
Как осуществляется связь математической модели и реальности?
Самые важные математические модели всегда обладают качеством универсальности. То есть, совершенно разные феномены могут быть описаны одной математической моделью.
Однако стоит помнить, что модель — объект, она может иметь собственные качества и свойства, которые могут не относиться к реальному моделируемому объекту.
Часто математические модели представляют в виде:
Представим основные понятия, которые важны для изучения данной темы:
Виды математических моделей, классификация
Существует несколько классификаций математических моделей. Рассмотрим некоторые из них.
Формальная типология
Основа данной классификации — какие математические средства используются для создания модели. Для создания схем в формальной классификации часто используется прием дихотомии.
Дихотомия — раздвоение, разделение чего-то на две части. Например, графиков.
К известным типам дихотомии относятся:
| Линейные | Нелинейные |
| Сосредоточенные | Распределенные |
| Детерминированные | Стохастические |
| Статические | Динамические |
| Дискретные | Непрерывные |
Типология по методу представления объекта
В рамках данной классификации выделяют структурные и функциональные модели.
Эти парадигмы также имеют название «черные ящики».
Содержательные, а также формальные модели
Многие авторы, которые описывают процесс моделирования в математике, отмечают, что для начала нужно построить специальную образцовую конструкцию, так называемую содержательную модель.
В разных учебных изданиях идеальный объект называется по-разному. Встречаются такие примеры как умозрительная модель, концептуальная модель, а также предмодель.
Конечная математическая схема будет назваться формальной моделью (математическая модель). Она получается в результате представления предмодели с помощью формального языка.
Построить умозрительную модель можно с помощью уже готового набора идеализаций. Например, в механике существуют идеальные пружины, маятники, твердые тела и тд, которые представляют собой готовые заготовки для построения содержательной модели.
Однако есть научные области, в которых сложно построить содержательные модели, потому что в них нет полноценных формализованных доктрин. К таким дисциплинам относятся биология, физика, психология, экономика и многие другие).
Содержательная типология
В работах английского физика Рудольфа Эрнста Пайерлса можно найти некоторые типологии математических моделей, которые используются в физике и других естественных науках. Советские ученые Александр Горбань и Рэм Хлебопрос расширили классификацию Пайерлса. Данная типология акцентирует свое внимание на процессе выстраивания содержательной модели. Итак, существуют следующие типы математических моделей:
Сложность моделируемой системы
Выделяются три уровня систем по сложности:
Советский академик Александр Андронов выделил три типа неустойчивых моделей:
Неустойчивые модели называют негрубыми. Устойчивые модели — мягкие.
Какие еще бывают модели?
Это ряд прототипов, которые выделяются по принципу применения.
Также выделяют материальные и информационные модели. Натуральные — муляжи, макеты. А информационные — прототипы, которые заменяют реальность формально (то есть словесно, графически и т.д.).
Какие параметры нужны для построения математической модели
Рассмотрим принципы построения математических моделей:
Также все математические модели должны отличаться следующими признаками адекватностью, конечностью, полнотой, упрощенностью, гибкостью.
Алгоритм составления, основные моменты
Для того чтобы составить математическую модель необходимо перевести данные задачи в вид математической формы. То есть переделать слова в формулу, уравнение и т.д. Необходимо установить математические связи между всеми условиями задачи.
Стоит помнить, что формула, уравнение математической модели должно полностью соответствовать тексту задачи, потому что иначе цель исследования изменится, а значит и задачу мы будем решать другую.
Представим алгоритм решения математической модели:
Попробуем составить математическую модель на примере простой задачи:
Иван Федорович вернулся с охоты и показал своей семье добычу. Оказалось, что он принес 10 тушек зайцев, которые живут в тайге, 50 % всей добычи — из тундры, а из местного леса, где охотился Иван Федорович нет ни одного животного. Сколько всего дичи купил Иван Федорович в магазине «Мясо диких животных?».
Данный текст нужно представить в виде уравнения. Для этого необходимо установить математические связи между всеми условиями задачи.
Обобщение — для того, чтобы построить математическую модель, нужно выбросить всю ненужную информацию из задачи, оставить только нужное и заменяем на математический объект.
Урок 13
Информационное моделирование на компьютере
Содержание урока
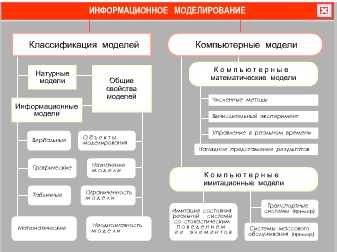
Информационное моделирование на компьютере. Компьютерная математическая модель
Информационное моделирование на компьютере
Компьютерная математическая модель
Изучаемые вопросы:
— Разновидности компьютерных моделей.
— Компьютерная математическая модель и вычислительный эксперимент.
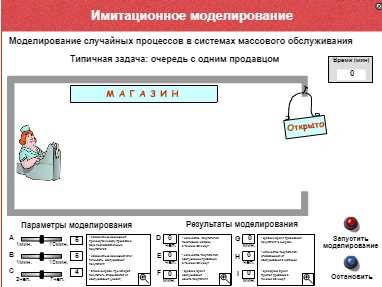
— Имитационное моделирование.



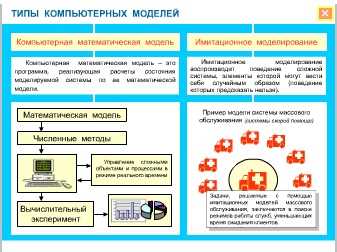


 Математическая модель — это описание моделируемого процесса на языке математики.
Математическая модель — это описание моделируемого процесса на языке математики. Использование компьютерной математической модели для исследования поведения объекта моделирования называется вычислительным экспериментом. Говорят также: численный эксперимент.
Использование компьютерной математической модели для исследования поведения объекта моделирования называется вычислительным экспериментом. Говорят также: численный эксперимент.
 Информационное моделирование на компьютере. Управление на основе моделей
Информационное моделирование на компьютере. Управление на основе моделей