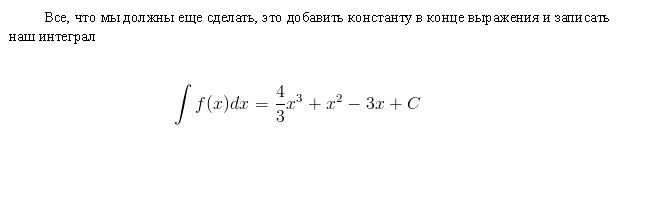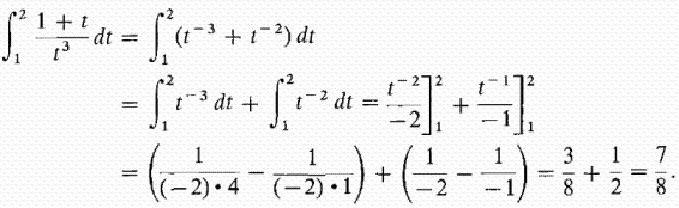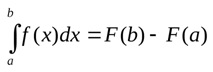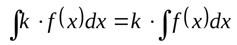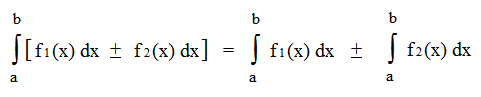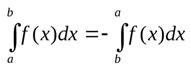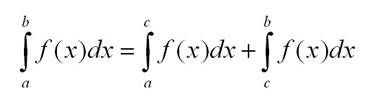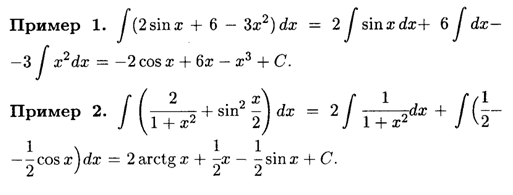Для чего нужна таблица интегралов
Таблица интегралов
Основные формулы интегралов
Интегрирование — это процесс нахождения интеграла, что является одной из основных операций математического анализа. При вычислении определенного интеграла определяется площадь криволинейной трапеции, которая ограничивается сверху кривой (графиком заданной функции), снизу осью х, справа и слева вертикальными прямыми, которые параллельны оси y в заданных точках.
Знания основных формул интегрирования помогут взять неопределенный и вычислить определенный интегралы. Решение задач, где используются интегралы всегда начинается с взятия неопределенного интеграла, поэтому в этом разделе представлены основные формулы неопределенных интегралов, где С — это произвольная константа интегрирования, то есть число, которое можно задать, если нам будет известны дополнительные условия, например, значения функции в конкретной точке.
Ниже представлена таблица основных интегралов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Правила интегрирования функций
Для того чтобы взять интеграл, не всегда хватает знания таблицы основных формул, также необходимо знать свойства интегралов и правила интегрирования различных функций.
Метод замены переменной помогает упростить сложные интегралы и свести их либо к более простым, либо к табличным значениям, которые можно сразу проинтегрировать и вычислить значения, если нам известны пределы интегрирования (для определенного интеграла). Он производится двумя способами: подведение функции под знак дифференциала и собственно замена переменной.
Интегралы элементарных функций
Первообразные рациональных функций
Логарифмы
Основные интегралы с логарифмическими функциями, которые нужно знать:
Также рассмотрим частные случаи интегрирования логарифмических функций, примером могут служить такие интегралы:
Что такое интеграл? Интегралы с подробным решением. Таблица интегралов
Слово «интеграл» происходит от латинского integralis – целостный. Это название предложил в 17 в. ученик великого Лейбница (и также выдающийся математик) И. Бернулли. А что такое интеграл в современном понимании? Ниже мы постараемся дать всесторонний ответ на этот вопрос.
Исторические предпосылки возникновения понятия интеграла
В начале 17 в. в рассмотрении ведущих ученых находилось большое число физических (прежде всего механических) задач, в которых нужно было исследовать зависимости одних величин от других. Самыми наглядными и насущными проблемами были определение мгновенной скорости неравномерного движения тела в любой момент времени и обратная этой задача нахождения величины пути, пройденного телом за определенный промежуток времени при таком движении. Сегодня мы уже знаем, что такое интеграл от скорости движения – это и есть пройденный путь. Но понимание того, как его вычислять, зная скорость в каждый момент времени, появилось не сразу.
Поначалу из рассмотрения таких зависимостей физических величин, например, пути от скорости, было сформировано математическое понятие функции y = f(x). Исследование свойств различных функций привело к зарождению математического анализа. Ученые активно искали способы изучения свойств различных функций.
Как возникло вычисление интегралов и производных?
После создания Декартом основ аналитической геометрии и появления возможности изображать функциональные зависимости графически в осях декартовой системы координат, перед исследователями встали две крупные новые задачи: как провести касательную к кривой линии в любой ее точке и как найти площадь фигуры, ограниченной сверху этой кривой и прямыми, параллельными осям координат. Неожиданным образом оказалось, что первая из них эквивалентна нахождению мгновенной скорости, а вторая – нахождению пройденного пути. Ведь он при неравномерном движении изображался в декартовых осях координат «расстояние» и «время» некоторой кривой линией.
Гением Лейбница и Ньютона в середине 17 в. были созданы методы, позволившие решать обе эти задачи. Оказалось, что для проведения касательной к кривой в точке нужно найти величину так называемой производной от функции, описывающей эту кривую, в рассматриваемой ее точке, и эта величина оказывается равной скорости изменения функции, т. е. применительно к зависимости «путь от скорости» собственно мгновенной скоростью тела.
Для нахождения же площади, ограниченной кривой линией, следовало вычислить определенный интеграл, который давал ее точную величину. Производная и интеграл – основные понятия дифференциального и интегрального исчисления, являющихся базисом современного матанализа – важнейшего раздела высшей математики.
Площадь под кривой линией
Итак, как же определить ее точную величину? Попробуем раскрыть процесс ее вычисления через интеграл подробно, с самых азов.
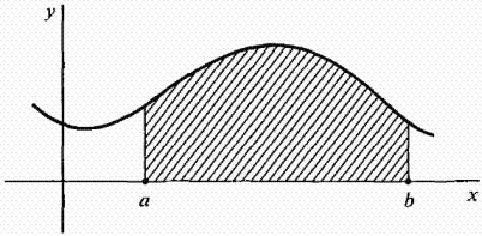
Пусть f является непрерывной на отрезке [ab] функцией. Рассмотрим кривую у = f(x), изображенную на рисунке ниже. Как найти площадь области, ограниченной кривой ), осью х, и линиями х = а и х = b? То есть площадь заштрихованной фигуры на рисунке.
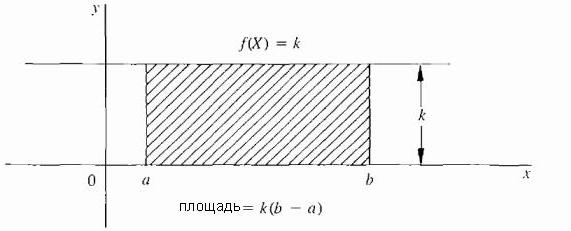
Самый простой случай, когда f является постоянной функцией; то есть, кривая есть горизонтальная линия f(X) = k, где k постоянная и k ≥ 0, как показано на рисунке ниже.
Области некоторых других простых фигур, таких как треугольник, трапеция и полуокружность, даются формулами из планиметрии.
Площадь под любой непрерывной кривой у = f(х) дается определенным интегралом, который записывается так же, как обычный интеграл.
Риманова сумма
Прежде чем погрузиться в подробный ответ на вопрос, что такое интеграл, выделим некоторые основные идеи.
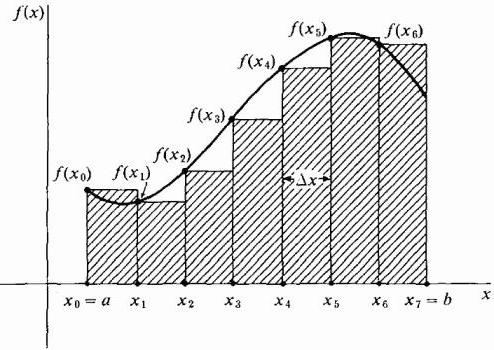
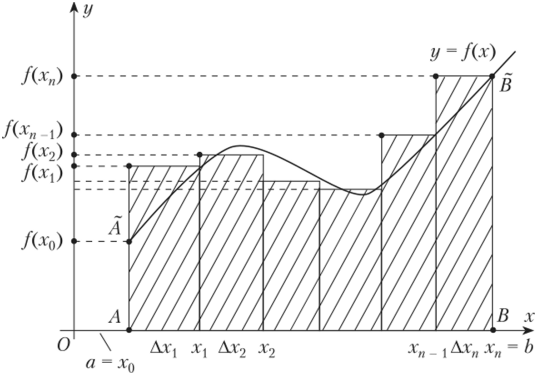
Во-первых, область под кривой делится на некоторое число n вертикальных полос достаточно малой ширины Δx. Далее каждая вертикальная полоса заменяется вертикальным прямоугольником высотой f(х), шириной Δx, и площадью f(х)dx. Следующим шагом является формирование суммы площадей всех этих прямоугольников, называемой Римановой суммой (смотрите рисунки ниже).
Рисуя наши прямоугольники шириной Δx, мы можем брать их высоту, равную значению функции на левом краю каждой полоски, т. е. на кривой будут лежать крайние левые точки их верхних коротких сторон шириной Δx. При этом на участке, где функция растет, и ее кривая является выпуклой, все прямоугольники оказываются ниже этой кривой, т. е. их сумма будет заведомо меньшей точной величины площади под кривой на этом участке (см. рисунок ниже). Такой способ аппроксимации называется левосторонним.
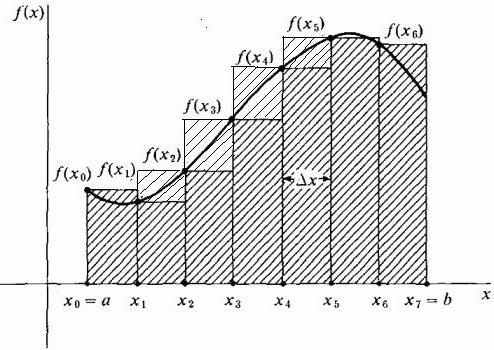
В принципе, можно нарисовать аппроксимирующие прямоугольники таким образом, чтобы на кривой лежали крайние правые точки их верхних коротких сторон шириной Δx. Тогда они будут выше кривой, и приближение площади на этом участке окажется больше ее точной величины, как показано на рисунке ниже. Этот способ носит название правостороннего.
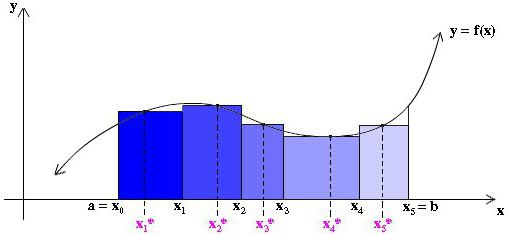
Но мы можем также взять высоту каждого из аппроксимирующих прямоугольников, равной просто некоторому значению функции в произвольной точке x*i внутри соответствующей полоски Δxi (смотри рис. ниже). При этом мы даже можем не брать одинаковую ширину всех полосок.
Составим Риманову сумму:
Переход от Римановой суммы к определенному интегралу
В высшей математике доказывается теорема, которая гласит, что если при неограниченном возрастании числа n аппроксимирующих прямоугольников наибольшая их ширина стремится к нулю, то Риманова сумма An стремится к некоторому пределу A. Число A – одно и то же при любом способе образования аппроксимирующих прямоугольников и при любом выборе точек x*i.
Наглядное пояснение теоремы дает рисунок ниже.
Из него видно, что, чем уже прямоугольники, тем ближе площадь ступенчатой фигуры к площади под кривой. При числе прямоугольников n→∞ их ширина Δxi →0, а предел A суммы An численно равен искомой площади. Этот предел и есть определенный интеграл функции f (х):
Символ интеграла, представляющий собой видоизмененную курсивную литеру S, был введен Лейбницем. Ставить сверху и снизу обозначения интеграла его пределы предложил Ж. Б. Фурье. При этом ясно указывается начальное и конечное значение x.
Геометрическое и механическое истолкование определенного интеграла
Попробуем дать развернутый ответ на вопрос о том, что такое интеграл? Рассмотрим интеграл на отрезке [a,b] от положительной внутри него функции f(х), причем считаем, что верхний предел больше нижнего a n
Давайте рассмотрим простые неопределенные интегралы, примеры взятия которых показаны ниже.
Пусть нужно найти интеграл от функции:
Начнем с первого слагаемого. Мы смотрим на показатель степени 2 и увеличиваем его на 1, затем делим первый член на результирующий показатель 3. Получаем: 4(x 3 ) / 3.
Последний член имеет множитель х, но мы просто не видим его. Мы можем представить себе последнее слагаемое как (-3x 0 ). Это эквивалентно (-3)∙(1). Если мы используем правило интегрирования, мы добавим 1 к показателю, чтобы поднять его до первой степени, а затем разделим последний член на 1. Получим 3x.
Это правило интегрирования работает для всех значений n, кроме n = – 1 (потому что мы не можем разделить на 0).
Мы рассмотрели самые простой пример нахождения интеграла. Вообще же решение интегралов является делом непростым, и в нем хорошим подспорьем является уже накопленный в математике опыт.
Таблицы интегралов
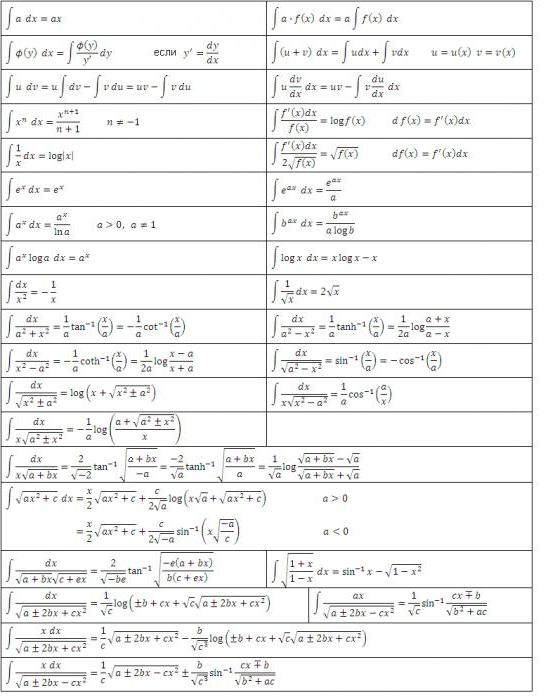
В разделе выше мы видели, что из каждой формулы дифференцирования получается соответствующая формула интегрирования. Поэтому все возможные их варианты уже давно получены и сведены в соответствующие таблицы. Нижеприведенная таблица интегралов содержит формулы интегрирования основных алгебраических функций. Эти формулы нужно знать на память, заучивая их постепенно, по мере их закрепления упражнениями.
Еще одна таблица интегралов содержит основные тригонометрические функции:
Как же вычислить определенный интеграл
Оказывается, сделать это, умея интегрировать, т. е. находить неопределенные интегралы, очень просто. И помогает в этом формула основателей интегро-дифференциального исчисления Ньютона и Лейбница
Согласно ей, вычисление искомого интеграла состоит на первом этапе в нахождении неопределенного, последующем вычислении значения найденной первообразной F(x) при подстановке x, равного сначала верхнему пределу, затем нижнему и, наконец, в определении разности этих значений. При этом константу С можно не записывать. т.к. она пропадает при выполнении вычитания.
Рассмотрим некоторые интегралы с подробным решением.
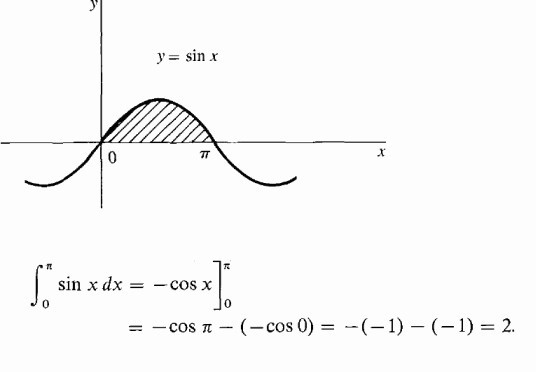
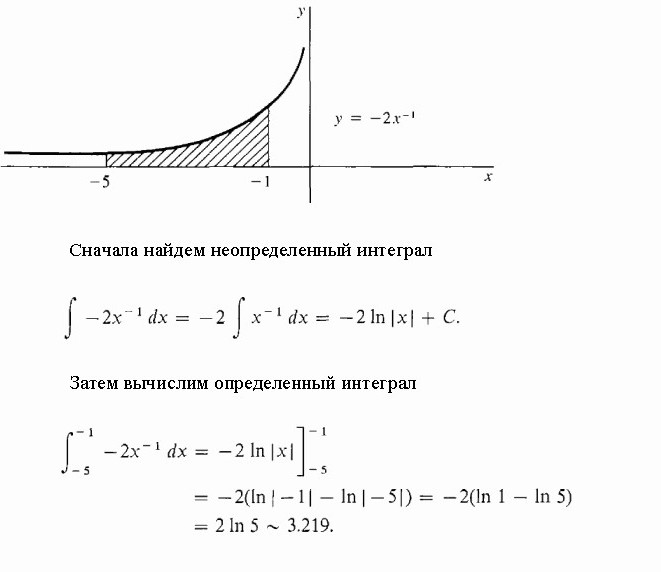
Найдем площадь участка под одной полуволной синусоидой.
y=(1+t)/t 3 от t=1 до t=2.
О несобственных интегралах
Мы говорили об определенном интеграле для конечного промежутка [a,b] от непрерывной на нем функции f(х). Но ряд конкретных задач приводит к необходимости расширить понятие интеграла на случай, когда пределы (один или оба) равны бесконечности, или при разрывной функции. Например, при вычислении площадей под кривыми, асимптотически приближающимися к осям координат. Для распространения понятия интеграла на этот случай, кроме предельного перехода при вычислении Римановой суммы аппроксимирующих прямоугольников, выполняется еще один. При таком двукратном переходе к пределу получается несобственный интеграл. В противоположность ему все интегралы, о которых говорилось выше, называются собственными.
Интегралы – что это, как решать, примеры решений и объяснение для чайников
За 4 минуты вы узнаете, что такое интегрирование. Как интеграл связан с производными. Чем отличается определенный интеграл от неопределенного. 5 примеров вычисления интегралов
Почему вы не знаете, как решать интегралы
А для чего нужны интегралы? Попробуйте сами себе ответить на этот вопрос.
Объясняя тему интегралов, учителя перечисляют малополезные школьным умам области применения. Среди них:
Связать все эти процессы не всегда получается, поэтому многие ученики путаются, даже при наличии всех базовых знаний для понимания интеграла.
Главная причина незнания – отсутствие понимания практической значимости интегралов.
Нужна помощь в написании работы?
Написание учебной работы за 1 день от 100 рублей. Посмотрите отзывы наших клиентов и узнайте стоимость вашей работы.
Интеграл – что это?
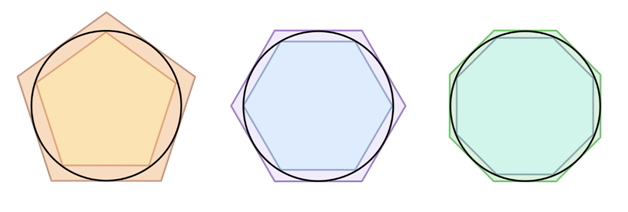
Предпосылки. Потребность в интегрировании возникла в Древней Греции. В то время Архимед начал применять для нахождения площади окружности методы, похожие по сути на современные интегральные исчисления. Основным подходом для определения площади неровных фигур тогда был «Метод исчерпывания», который достаточно лёгок для понимания.
Суть метода. В данную фигуру вписывается монотонная последовательность других фигур, а затем вычисляется предел последовательности их площадей. Этот предел и принимался за площадь данной фигуры.
Метод исчерпывания для определения площади круга
В этом методе легко прослеживается идея интегрального исчисления, которая заключается в нахождении предела бесконечной суммы. В дальнейшем эта идея применялась учёными для решения прикладных задач астронавтики, экономики, механики и др.
Современный интеграл. Классическая теория интегрирования была сформулирована в общем виде Ньютоном и Лейбницем. Она опиралась на существовавшие тогда законы дифференциального исчисления. Для её понимания, необходимо иметь некоторые базовые знания, которые помогут математическим языком описать визуальные и интуитивные представления об интегралах.
Объясняем понятие «Интеграл»
Процесс нахождения производной называется дифференцированием, а нахождение первообразной – интегрированием.
Интеграл математическим языком – это первообразная функции (то, что было до производной) + константа «C».
Интеграл простыми словами – это площадь криволинейной фигуры. Неопределенный интеграл – вся площадь. Определенный интеграл – площадь в заданном участке.
Интеграл записывается так:
Каждая подынтегральная функция умножается на компонент «dx». Он показывает, по какой переменной осуществляется интегрирование. «dx» – это приращение аргумента. Вместо X может быть любой другой аргумент, например t (время).
Неопределённый интеграл
Неопределенный интеграл не имеет границ интегрирования.
Для решения неопределённых интегралов достаточно найти первообразную подынтегральной функции и прибавить к ней «C».
Определённый интеграл
В определенном интеграле на знаке интегрирования пишут ограничения «a» и «b». Они указаны на оси X в графике ниже.
Точки A и B на оси X – есть ограничение зоны определения интеграла
Для вычисления определенного интеграла необходимо найти первообразную, подставить в неё значения «a» и «b» и найти разность. В математике это называется формулой Ньютона-Лейбница:
Таблица интегралов для студентов (основные формулы)
Скачайте формулы интегралов, они вам еще пригодятся
Как вычислять интеграл правильно
Существует несколько простейших операций для преобразования интегралов. Вот основные из них:
Вынесение константы из-под знака интеграла
Разложение интеграла суммы на сумму интегралов
Если поменять местами a и b, знак изменится
Можно разбить интеграл на промежутки следующим образом
Это простейшие свойства, на основе которых потом будут формулироваться более сложные теоремы и методы исчисления.
Примеры вычисления интегралов
Решение неопределенного интеграла
Решение определенного интеграла
Базовые понятия для понимания темы
Чтобы вы поняли суть интегрирования и не закрыли страницу от непонимания, мы объясним ряд базовых понятий. Что такое функция, производная, предел и первообразная.
Функция – правило, по которому все элементы из одного множества соотносятся со всеми элементами из другого.
Производная – функция, описывающая скорость изменения другой функции в каждой конкретной точке. Если говорить строгим языком, – это предел отношения приращения функции к приращению аргумента. Он вычисляется вручную, но проще использовать таблицу производных, в которой собрано большинство стандартных функций.
Приращение – количественное изменение функции при некотором изменении аргумента.
Предел – величина, к которой стремиться значение функции, при стремлении аргумента к определённому значению.
Пример предела: допустим при X равном 1, Y будет равно 2. Но что, если X не равен 1, а стремится к 1, то есть никогда её не достигает? В этом случае y никогда не достигнет 2, а будет только стремиться к этой величине. На математическом языке это записывается так: limY(X), при X –> 1 = 2. Читается: предел функции Y(X), при x стремящемся к 1, равен 2.
Как уже было сказано, производная – это функция, описывающая другую функцию. Изначальная функция может быть производной для какой-либо другой функции. Эта другая функция называется первообразной.
Заключение
Найти интегралы не трудно. Если вы не поняли, как это делать, прочитайте статью еще раз. Со второго раза становится понятнее. Запомните! Решение интегралов сводится к простым преобразованиям подынтегральной функции и поиска её в таблице интегралов.
Если текстовое объяснение вам не заходит, посмотрите видео о смысле интеграла и производной:
Как использовать таблицу интегралов?
Не просите маня в х найти какой-нибудь интеграл. Я не умею находить интегралы, я могу только над ними по прикалываться. Прежде, чем здесь появится таблица неопределенных интегралов, нужно представить определение неопределенного интеграла.
Прямо каламбур получился. Неопределенным интеграл называется так не потому, что определение для него никто не придумал, а потому, что с ним нельзя точно определиться. Математики меня заклюют за такое разъяснение.
Таблица интегралов
 |
| Неопределенный интеграл и его свойства |
Как видите, неопределенный интеграл представляет из себя совокупность первообразных для заданной функции. Дальше идет таблица основных неопределенных интегралов.
 |
| Таблица основных неопределенных интегралов |
Если вы любите по вечерам вместо семечек щелкать неопределенные интегралы, тогда большая таблица интегралов для вас. Если вы где-то учитесь, настоятельно рекомендую пользоваться большой таблицей интегралов в качестве ответов, которые обычно размещают в конце учебника. Помните, что вы не в детском садике и задачку без действий вам никто не задаст. Даже в задаче на одно действие между условием и ответом записывают это действие.
Вот большая таблица неопределенных интегралов. Эта таблица интегралов содержит 147 представителей этой математической фауны. Я подозреваю, что коллекция эта далеко не полная, но некоторые самые популярные виды интегралов в ней присутствуют.
Нажимаете на ссылку — откроется картинка, по виду очень похожая на размотанный рулон туалетной бумаги. Наводите курсор на эту ленту, курсор превращается в лупу со знаком «плюс», жмете. Теперь вы в царстве интегралов.
Сохранить память о столь увлекательном путешествии можно при помощи правой кнопки мыши и строчки меню «Сохранить изображение как…». Всё, Третьяковская галерея интегралов переселилась в ваш компьютер.
Это для тех, кто не любит читать всё то, что я пишу. Таблица интегралов разбита на 12 групп, все их мы рассмотрим более подробно на отдельных страницах.
Как найти неопределенный интеграл? Очень просто. Тупо берете формулу, тупо подставляете в пример. Лично я так делал. Иногда можно чего-то там перегруппировать, упростить, вынести за знак интеграла…
Название самого лучшего в мире искателя интегралов я не претендовал, о чем нисколько не жалею. Вообще, живых интегралов я за свою жизнь так и не встретил. Все они для меня вымерли, как динозавры, сразу же после окончания учебы. Да, я ещё кое-что о них помню. Только и всего.
Очень интересен каламбур, написанный буковками под таблицей основных неопределенных интегралов. На первый взгляд получается, что первообразная на первообразной сидит и первообразной погоняет. Ясно, что записанное выражение и дураку понятно.
Но бывают ещё и особо одаренные представители рода человеческого, типа меня. У меня просто мозги отключаются, когда я вижу или читаю подобные фразы. Наверное, инстинкт самосохранения срабатывает — мозг боится собственного вывиха.
Долго вспоминал, где у меня лево, где право. Через пару дней напряженной умственной работы, я пришел к выводу, что в левой части описывается ситуация, когда мы точно знаем, от какой первообразной функции мы получили производную.
В правой части мы пытаемся угадать, какой первообразной функции принадлежит производная. На динозаврах это гораздо понятнее. Если у нас есть живой динозавр, то мы точно знаем, как он выглядит, и точно можем сказать, как через десятки миллионов лет будут выглядеть его останки.
Но вот когда мы сегодня находим останки динозавров, мы не можем точно сказать, как они выглядели — окраску, голос, запах по останкам определить не возможно. Знак равенства стоит на том основании, что из всех возможных вариантов один точно правильный.
В отличии от динозавров, математические функции математики представляют в абстрактном виде, вне времени — одновременно и настоящее, и будущее, и прошлое. Теперь эта же мысль, но языком математических формул. Используем определение и свойства неопределенных интегралов. Возьмем первообразную функцию с константой и посмотрим, что происходит.
 |
| Первообразная функция |
Здесь на первое место выступает порядок выполнения математических действий. Если мы сперва дифференцируем первообразную функцию, то константа теряется. После интегрирования её нужно восстанавливать для сохранения равенства.
Если применить свойства неопределенного интеграла и взаимно сократить интегрирование и дифференцирование, то первообразная останется в своем первоначальном виде, с константой. Здесь получается фокус с тузом в рукаве.
В определении неопределенного интеграла константа является частью первообразной функции F(x) и отдельно не выделяется — туз спрятан в рукаве. После интегрирования мы добавляем константу, потерявшуюся при дифференцировании — туз достаем из рукава на всеобщее обозрение.
В этом случае главным является не сам фокус, а факт присутствия туза у фокусника как до, так и после демонстрации трюка. Что такое константа? Это число. Геометрически при помощи изменения константы можно сместить график функции F(x) вдоль оси игреков вниз или вверх.
В определении неопределенного интеграла указано, что совокупность всех этих первообразных и представляет из себя этот злополучный интеграл. Но это только одна сторона медали. В определении не указывается, что вся совокупность первообразных рассматривается в одной, кем-то когда-то выбранной, системе координат.
А если мы выберем одну первообразную, тогда изменение константы будет смещать систему координат. С точки зрения выбранной первообразной, неопределенный интеграл — это совокупность всех систем координат, в которых может рассматриваться данная первообразная функция.
Чудеса относительности. Если мы сидим попой на поверхности Земли, то мы видим, как Солнце бегает по небу. Если мы сидим попой на Солнце (не бойтесь поджариться, ведь математика — абстрактная наука и позволяет сидеть на чем угодно), то мы видим, как Земля вращается вокруг собственной оси.
Всё зависит от выбранной нами точки зрения, что в математике соответствует выбору системы координат. С учетом относительности влияния константы на сладкую парочку «функция — система координат», первое предложение в определении неопределенного интеграла можно записать так:
Неопределенный интеграл для функции f(x) — это совокупность всех первообразных данной функции или совокупность всех систем координат данной первообразной функции.
Не знаю, как посмотрят на такое развитие сюжета математики, но получилось слишком заумно. Всё это дело можно упростить, если отказаться от пыток восстановить константу в первообразной функции. Ещё раз проконтролируем свои действия.
Если у нас есть первообразная функция с константой или без, мы можем точно сказать, как выглядит её производная. Если у нас есть производная, мы не можем точно сказать, от какой именно первообразной она получена.
Всё дело заключается в том, что при взятии производной происходит изменение системы координат. Если мы рассматриваем производную f(x) в измененной системе координат, то восстановить первоначальную систему координат первообразной функции F(x) невозможно.
Нельзя воскресить мертвое. Вместо математической точности у нас получается гадание на кофейной гуще. И это гадание выражается в прибавлении константы к скелету первообразной функции. Задачу эту можно решить на уровне задних парт третьего класса.
Почему задних парт? Они находятся дальше всех от испепеляющего светоча знаний, льющегося с классной доски. Почему третьего класса? У них ещё не выработан благоговейный трепет перед учебниками. Просто начинаем фантазировать. Придумываем какое-нибудь новое определение и при помощи него разруливаем ситуацию.
Функция в собственной системе координат Fo(x) — это функция, у которой константа приравнивается к нулю. Так сказать, функция в собственном соку. Классическим примером функций в собственной системе координат можно считать тригонометрические функции. При изучении они рассматриваются без константы.
Поскольку определение неопределенного интеграла уже написано и правила хорошего тона настоятельно не рекомендуют его рихтовать, придумаем еще одно определение какой-нибудь промежуточной фигни. Пусть эта фигня будет называться «определенная первообразная«. Теперь берем определение неопределенного интеграла и на его основе пишем свое определение определенной первообразной.
Определенная первообразная для функции f(x) — это первообразная данной функции в собственной системе координат Fo(x). Если функция f(x) определена и непрерывна на промежутке (a, b) и F(x) — её первообразная, то есть F'(x)=f(x) при a меньше x меньше b
 |
| Определенная первообразная |
От определенной первообразной можно двигаться налево к неопределенному интегралу путем добавления константы или направо к определенному интегралу путем обозначения пределов интегрирования. Выглядит это приблизительно так.
 |
| Свойства определенной первообразной |
В геометрическом смысле определенная первообразная является формулой для вычисления площади фигуры, ограниченной осями координат, графиком функции f(x) и прямой х=х. В последнем равенстве с левой стороны находится просто буква икс, обозначающая переменную, с правой стороны — её численное значение.
Дальше ещё несколько слов о константе в неопределенном интеграле. При дифференцировании функции константа превращается в ноль. В математике существует первая, вторая, третья и так далее, производные. Можно предположить, что столько же существует и неопределенных интегралов. Берем результат интегрирования и снова интегрируем. Вот что может получиться…
Ветхий Завет от Матана.
Вначале ничего не было. Потом было слово. Точнее, два слова — Неопределенный Интеграл. И создал Неопределенный Интеграл константу. А потом Он создал переменную. И стала переменная плюс константа. А потом Неопределенный Интеграл создал…
 |
| Первообразная константы |
Вот так и появился этот мир, в котором мы живем. Аминь. Пардон, плюс константа. Если вас не устраивает такая история сотворения мира, эти же формулы можно трактовать как историю Большого Взрыва. Ведь ученые уверяют, что началось всё с точки, то есть с нуля.
Сергей Манулов, давний друг этого сайта, предлагал мне опубликовать в одной таблице интегралы рядом с производными. Так действительно будет нагляднее и понятней. Но здесь есть два момента. Во-первых, таблица получится такой широкой, что в этот сайт явно не влезет.
Во-вторых, насколько я помню, таблица производных несколько меньше, чем таблица интегралов. Ну не любят математики играть в производные.
Кого интересует исследование всяких каракуль, пусть даже и обличенных в математические формулы? А вот игры в интегралы среди математиков очень даже популярны. По своей популярности они могут уступать разве что играм в комплексные числа.
Наверное, так получается потому, что при помощи определенных интегралов можно находить площади криволинейных трапеций или что-то там ещё. Математики играют в свои любимые игрушки и вроде как полезным делом заняты.
Что нужно помнить о неопределенных интегралах? Как молитва заканчивается словом «Аминь», так любой неопределенный интеграл заканчивается словами «плюс константа».