Для чего нужна теорема лагранжа

Для чего нужна теорема лагранжа

Проверить справедливость теоремы Лагранжа для функции \[f\left( x \right) = — 3x + 5\] на отрезке \(\left[ <1,4>\right].\) Если теорема соблюдается, найти точку \(\xi,\) удовлетворяющую условиям теоремы.

Составить формулу конечных приращений для квадратичной функции \(f\left( x \right) = a + bx + c\) при произвольных значениях \(x\) и \(\Delta x.\)

С помощью формулы Лагранжа (или формулы конечных приращений) можно вычислить значение функции в точке \(x + \Delta x,\) если известно значение функции \(f\left( x \right)\) в точке \(x\) и значение производной \(f’\left( \xi \right)\) в некоторой промежуточной \(\xi.\) Запишем данную формулу в таком виде: \[f\left( \right) = f\left( x \right) + f’\left( \xi \right)\Delta x.\] Найдем теперь координату \(\xi\) (в которой вычисляется производная) для квадратичной функции. Производная квадратичной функции записывается в виде \[ = <<\left( + bx + c> \right)^\prime > > = <2ax + b.>\] Подставляя в формулу Лагранжа выражения для функции \(f\left( x \right)\) и ее производной, получаем: \[ \right)^2> + b\left( \right) + c = a + bx + c + \left( <2a\xi + b>\right)\Delta x,>\;\; <\Rightarrow \cancel<\color>> + 2ax\Delta x + a <\left( <\Delta x>\right)^2> + \cancel<\color> + \cancel<\color> + \cancel<\color> = \cancel<\color>> + \cancel<\color> + \cancel<\color> + 2a\xi \Delta x + \cancel<\color>,>\;\; <\Rightarrow 2ax\Delta x + a<\left( <\Delta x>\right)^2> = 2a\xi \Delta x,>\;\; <\Rightarrow a\Delta x\left( <2x + \Delta x>\right) = 2a\xi \Delta x,>\;\; <\Rightarrow 2\xi = 2x + \Delta x,>\;\; <\Rightarrow 2\xi = 2\left( ><2>> \right),>\;\; <\Rightarrow \xi = x + \frac<<\Delta x>><2>.> \] Следовательно, в данном случае производную нужно вычислять в точке с координатой \(\xi = x + \large\frac<<\Delta x>><2>\normalsize,\) т.е. смещенной относительно \(x\) на половину приращения \(\Delta x.\) Этот результат справедлив для любой квадратичной функции при произвольных значениях \(x\) и \(\Delta x.\) Таким образом, окончательная формула для квадратичной функции имеет вид \[ \right) > = ><2>> \right)\Delta x.> \] В соответствии с теоремой Лагранжа, касательная, проведенная в точке \(\xi = x + \large\frac<<\Delta x>><2>\normalsize,\) будет параллельна хорде, соединяющей точки \(A\left( \right)\) и \(B\left( \right)> \right)\) (рисунок \(4\)).

Функция \(\) всюду непрерывна и дифференцируема. Показать, что если функция \(\) имеет два действительных корня, то ее производная \(\) имеет по крайней мере один корень.

Подчеркнем, что у производной может быть более одного корня (например, можно рассмотреть функцию \(f\left( x \right) = \sin x\) на отрезке \(\left[ <0,2\pi>\right],\) где производная имеет два корня). Теорема Лагранжа позволяет доказать существование по меньшей мере одного корня.

Функция \(\) непрерывна и дифференцируема на отрезке \(\left[ <2,10>\right].\) Известно, что \(f\left( 2 \right) = 8\) и производная на данном промежутке удовлетворяет условию \(f’\left( x \right) \le 4\) для всех \(x \in \left( <2,10>\right).\) Определить максимально возможное значение функции при \(x = 10.\)

Перепишем эту формулу в виде \[f\left( <10>\right) = f\left( 2 \right) + 8f’\left( \xi \right).\] Максимально возможное значение производной на данном интервале составляет \(f’\left( x \right) = 4.\) Следовательно, \[f\left( <10>\right) \le f\left( 2 \right) + 8 \cdot 4 = 4 + 32 = 40.\] Таким образом, максимально возможное значение функции на правой границе интервала равно \(40.\)

Источник

Теорема Лагранжа и ее следствия

Теорема(Лагранж) (о конечных приращениях). Если функция f(x) непрерывна на отрезке [a, b], дифференцируема на интервале (a, b), то найдется хотя бы одна точка с є (a, b) такая, что выполняется равенство

f(b) – f(a) = f’(с) (b – a) – формула Лагранжа (о конечном приращении).

Доказательство. Теорему Лагранжа можно рассматривать как частный случай теоремы Коши, если положить φ(х) = х. В этом случае

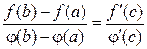
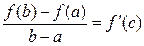
Подставляя эти значения в формулу , получаем или f(b) – f(a) = f’(с) (b – a).

Формула Лагранжа: приращение дифференцируемой функции на отрезке [a, b] равно приращению аргумента, умноженному на значение производной функции в некоторой внутренней точке этого отрезка.

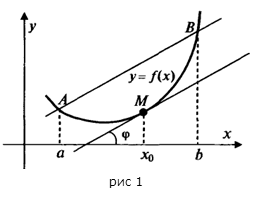
Геометрический смысл формулы Лагранжа.

Запишем формулу Лагранжа в виде 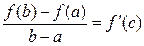, где a

Источник

Основные теоремы для дифференцируемых функций

Локальный экстремум и теорема Ферма.

Пусть существует число \(\delta > 0\) такое, что функция \(f(x)\) определена в \(\delta\)-окрестности точки \(x_<0>\), то есть на множестве \(U_<\delta>(x_0)=(x_0-\delta,x_<0>+\delta)\), и пусть для всех \(x\in U_<\delta>(x_0)\) выполняется неравенство
$$
f(x)\geq f(x_<0>).\label
$$
Тогда говорят, что функция \(f(x)\) имеет в точке \(x_0\) локальный минимум.

Аналогично, если существует число \(\delta > 0\) такое, что для всех \(x\in U_<\delta>(x_0)\) выполняется неравенство
$$
f(x)\leq f(x_<0>).\label
$$
то говорят, что функция \(f(x)\) имеет в точке \(x_0\) локальный максимум.

Локальный минимум и локальный максимум объединяются общим термином локальный экстремум. Функция \(y=f(x)\), график которой изображен на рис. 17.1, имеет локальные экстремумы в точках \(x_1=1,\ x_2=3,\ x_3=4\), а именно минимумы при \(x=1\) и \(x=4\) и максимум при \(x=3\).

Рис. 17.1

Если функция \(f(x)\) имеет локальный экстремум в точке \(x_0\) и дифференцируема в этой точке, то
$$
f'(x_0)=0\label
$$

\(\circ\) Пусть, например, функция \(f(x)\) имеет локальный минимум в точке \(x_0\). Тогда в силу \eqref для всех \(x\in(x_0-\delta,x_0+\delta)\) выполняется неравенство
$$
f(x)-f(x_<0>)\geq 0.\label
$$
Если \(x\in (x_0-\delta,x_0)\), то \(x-x_0 Рис. 17.2

Теорема Ферма имеет простой геометрический смысл: касательная к графику функции \(y=f(x)\) в точке локального экстремума \((x_0,f(x_0))\) параллельна оси абсцисс (рис. 17.2).

Теорема Ролля о нулях производной.

Если функция \(f(x)\) непрерывна на отрезке \([a,b]\), принимает в концах этого отрезка равные значения, то есть
$$
f(a)=f(b),\label
$$
и дифференцируема на интервале \((a,b)\), то существует точка \(\xi\in(a,b)\) такая, что
$$
f'(\xi)=0.\label
$$

\(\circ\) Обозначим \(M=\displaystyle \sup_f(x),\ m=\displaystyle \inf_f(x)\). По теореме Вейерштрасса на отрезке \([a,b]\) существуют такие точки \(c_<1>\) и \(c_<2>\), что \(f(c_<1>)=m,\ f(c_<2>)=M\).

Если \(m=M\), то \(f(x)=\operatorname\), и в качестве \(\xi\) можно взять любую точку интервала \((a,b)\).

Если \(m\neq M\), то \(m 0\) такое, что \(U_<\delta>(c_<1>)\subset (a,b)\). Так как для всех \(x\in U_<\delta>(c_)\) выполняется условие \(f(x)\geq f(c_<1>)=m\), то по теореме Ферма \(f'(c_<1>)=0\), то есть условие \eqref выполняется при \(\xi=c_<1>\). Аналогично рассматривается случай, когда \(c_<2>\in(a,b).\quad \bullet\)

Теорему Ролля можно кратко сформулировать так: между двумя точками, в которых дифференцируемая функция принимает равные значения, найдется хотя бы один нуль производной этой функции. Для случая \(f(a)=f(b)=0\) теорема формулируется еще короче: между двумя нулями дифференцируемой функции лежит хотя бы один нуль ее производной.

Рис. 17.3

Геометрический смысл теоремы Ролля: при условиях теоремы 2 существует значение \(\xi\in(a,b)\) такое, что касательная к графику функции \(y=f(x)\) в точке \((\xi,f(\xi))\) параллельна оси \(Ox\) (рис. 17.3).

Все условия теоремы Ролля существенны. На рис. 17.4—17.6 изображены графики функций, каждая из которых удовлетворяет всем условиям теоремы Ролля, кроме одного. Для всех этих функций не существует точки на интервале \((-2,2)\), в которой производная была бы равно нулю.

Формула конечных приращений Лагранжа.

Если функция \(f(x)\) непрерывна на отрезке \([a,b]\) и дифференцируема на интервале \((a,b)\), то в этом интервале найдется хотя бы одна точка \(\xi\) такая, что
$$
f(b)-f(a)=f'(\xi)(b-a).\label
$$

\(\circ\) Рассмотрим функцию
$$
\varphi(x)=f(x)+\lambda x,\nonumber
$$
где число \(\lambda\) выберем таким, чтобы выполнялось условие \(\varphi(a)=\varphi(b)\), то есть \(f(a)+\lambda a=f(b)+\lambda b\). Отсюда находим
$$
\lambda=-\frac.\label
$$
Так как функция \(\varphi(x)\) непрерывна на отрезке \([a,b]\), дифференцируема на интервале \((a,b)\) и принимает равные значения в концах этого интервала, то по теореме Ролля существует точка \(\xi\in(a,b)\) такая, что \(\varphi'(\xi)=f'(\xi)+\lambda=0\). Отсюда в силу условия \eqref получаем равенство
$$
f'(\xi)=\frac,\label
$$
равносильное равенству \eqref. \(\bullet\)

Правая часть, формулы \eqref равна угловому коэффициенту секущей, которая проходит через точки \(A(a,f(a))\) и \(B(b,f(b))\) графика функции \(y=f(x)\), а левая часть этой формулы равна угловому коэффициенту касательной к графику в точке \((\xi,f(\xi))\). Поэтому теорема Лагранжа имеет следующую геометрическую интерпретацию: существует значение \(\xi\in(a,b)\) такое, что касательная к графику функции \(y=f(x)\) в точке \((\xi,f(\xi))\) параллельна секущей (рис. 17.7), соединяющей точки \(A(a,f(a))\) и \(B(b,f(b))\).

Пусть функция \(f\) удовлетворяет условиям теоремы Лагранжа. Если \(x_<0>\in[a,b]\), а приращение \(\Delta x\neq 0\) таково, что точка \(x_<0>+\Delta x\) также принадлежит отрезку \([a,b]\), то, применив теорему Лагранжа к функции \(f(x)\) на отрезке \(l\) с концами \(x_0\) и \(x_0+\Delta x\) (\(\Delta x\) может быть и отрицательным), получим
$$
f(x_<0>+\Delta x)-f(x_<0>)=\Delta xf'(\xi),\label
$$
где \(\xi\) — некоторая внутренняя точка отрезка \(l\).

Пусть, \(\Delta x > 0\); тогда \(0 Пример 1.

Некоторые следствия из теоремы Лагранжа.

Если функция \(f(x)\) дифференцируема на интервале \((a,b)\) и \(f'(x)=0\) для всех \(x\in (a,b)\), то
$$
f(x)=C=\operatorname,\quad x\in (a,b).\nonumber
$$

\(\circ\) Пусть \(x_<0>\) — фиксированная точка интервала \((a,b)\), \(x\) — любая точка этого интервала. Применяя теорему Лагранжа к функции \(f(x)\) на отрезке с концами \(x_0\) и \(x\) получаем
$$
f(x)-f(x_0)=(x-x_0)f'(\xi),\nonumber
$$
где \(\xi\in(a,b),\ f'(\xi)=0\), откуда \(f(x)=f(x_<0>)=C\). \(\bullet\)

Если функция \(f(x)\) непрерывна на отрезке \([a,b]\), дифференцируема на интервале \((a,b)\) и для всех \(x\in (a,b)\) выполняется равенство \(f'(x)=k\), где \(k\) — постоянная, то
$$
f(x)=kx+B,\quad x\in[a,b],\nonumber
$$
то есть \(f\) — линейная функция.

\(\circ\) Применяя теорему Лагранжа к функции \(f\) на отрезке \([a,x]\), где \(a\leq x\leq b\), получаем \(f(x)-f(a)=k(x-a)\), откуда следует, что \(f(x)=kx+B\), где \(B=f(a)-ka\). \(\bullet\)

Пусть функция \(f(x)\) дифференцируема на интервале \((a,b)\), за исключением, быть может, точки \(x_0\in (a,b)\), и непрерывна в точке \(x_0\). Тогда если существует конечный или бесконечный
$$
\lim_-0>f'(x)=A,\label
$$
то в точке \(x_0\) существует левая производная, причем
$$
f_<->‘(x_<0>)=A.\label
$$

Аналогично, если существует
$$
\lim_+0>f'(x)=B,\label
$$
то
$$
f_<+>‘(x_0)=B.\label
$$
\(\circ\) Пусть приращение \(\Delta x\) таково, что \(\Delta x\neq 0\) и точка \(x_0+\Delta x\) принадлежит интервалу \((a,b)\). Запишем равенство \eqref в виде
$$
\frac+\Delta x)-f(x_<0>)><\Delta x>=f'(x_<0>+\theta\Delta x),\quad 0

Найти точки разрыва функции \(f'(x)\), если
$$
f(x)=\left\<\begin
\displaystyle x^2\sin<\frac<1>> & при\ x\neq 0,\\\nonumber
0 & при\ x=0.\nonumber
\end\right.
$$

\(\triangle\) Если \(x\neq 0\), то \(f'(x)=2\displaystyle \sin\frac<1>-\cos\frac<1>\), а если \(x=0\), то по определению производной \(f'(0)=\displaystyle\lim_\frac<\displaystyle x^2\sin<\frac<1>>>=0\). Следовательно, функция \(f'(x)\) определена на \(\mathbb\) и непрерывна при \(x\neq 0\). В точке \(x=0\) эта функция имеет разрыв второго рода, так как не существует предела функции
$$
f'(x)=2x\sin\frac<1>-\cos\frac<1>\quad при \ x\rightarrow 0.\quad \blacktriangle\nonumber
$$

Если функции \(\varphi\) и \(\psi\) дифференцируемы при \(x\geq x_0\) и удовлетворяют условиям \(\varphi(x_0)=\psi(x_0)\), \(\varphi'(x) > \psi(x)\) при \(x > x_0\), то \(\varphi(x) > \psi(x)\) при \(x > x_<0>\).

\(\circ\) Применяя теорему Лагранжа к функции \(f(x)=\varphi(x)-\psi(x)\) на отрезке \([x_0,x]\), где \(x > x_0\), получаем \(f(x)=f'(\xi)(x-x_0)\), так как \(f(x_0)=0\). Отсюда, учитывая, что
$$
\xi > х_0,\ f'(\xi)=\varphi'(\xi)-\psi'(\xi) > 0,\nonumber
$$
получаем \(f(x) > 0\), то есть \(\varphi(x) > \psi(x)\) при \(x > x_0\). \(\bullet\)

\(\triangle\) Пусть \(\varphi(х)=\operatorname(1+x)\), \(\psi(x)=x-\displaystyle \frac><2>\), тогда \(\varphi(0)=\psi(0)\), \(\displaystyle \varphi'(x)=\frac<1><1+x>\), \(\psi'(x)=1-x\), и при \(x > 0\) справедливо неравенство \(\displaystyle \frac<1> <1+x>> 1-x\), так как при \(x > 0\) это неравенство равносильно очевидному неравенству \(1 > 1-x^2\). Применяя следствие 4 к функциям \(\varphi(x)\) и \(\psi(x)\), получаем неравенство \eqref. \(\blacktriangle\)

Обобщенная формула конечных приращений (формула Коши).

Если функции \(f(x)\) и \(g(x)\) непрерывны на отрезке \([a,b]\), дифференцируемы на интервале \((a,b)\), причем \(g'(x)\neq 0\) во всех точках этого интервала, то найдется хотя бы одна точка \(\xi\in(a,b)\) такая, что
$$
\frac=\frac.\label
$$

Теорема Лагранжа — частный случай теоремы Коши \((g(x)=x)\).

Теорему Коши нельзя получить, применением теоремы Лагранжа к числителю и знаменателю дроби, стоящей в левой части равенства \eqref.

Действительно, эту дробь, по теореме Лагранжа можно записать в виде \(\displaystyle \frac)>)>\), где \(\xi_<1>\in (a,b),\ \xi_<2>\in (a,b)\), но, вообще говоря, \(\xi_<1>\neq\xi_<2>\).

Источник

Основные теоремы дифференциального исчисления

Теорема Ферма

Теорема Ферма. (О равенстве нулю производной)

Следствие. (Геометрический смысл теоремы Ферма)

В точке наибольшего и наименьшего значения, достигаемого внутри промежутка, касательная к графику функции параллельна оси абсцисс.

Теорема Ролля

Теорема Ролля. (О нуле производной функции, принимающей на концах отрезка равные значения)

Следствие. (Геометрический смысл теоремы Ролля)

Найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс.

Следствие.

Теорема Лагранжа

Теорема Лагранжа. (О конечных приращениях)

Следствие. (Геометрический смысл теоремы Лагранжа)

Доказанная формула называется формулой Лагранжа или формулой конечных приращений. Она может быть переписана в виде:

Теорема Коши

Теорема Коши. (Об отношении конечных приращений двух функций)

Если производная функции равна нулю на некотором промежутке, то функция является постоянной на этом промежутке.

Если две функции имеют равные производные на некотором промежутке, то они на этом промежутке отличаются друг от друга на некоторое слагаемое.

Источник

Теорема Лагранжа о порядке конечной группы

Пусть — группа, — ее подгруппа. Левым смежным классом подгруппы по элементу называют множество

Соответственно правый смежный класс подгруппы по элементу — это множество

Замечание. При использовании аддитивной записи групповой операции смежные классы записываются в виде (или ).

Из доказанных теорем о свойствах левых смежных классов, справедливых — подчеркнем это — для любой группы, вытекает простой, но очень важный результат для конечных групп.

Теорема 2.13 (теорема Лагранжа). Порядок конечной группы делится на порядок любой ее подгруппы.

Следствия теоремы Лагранжа

Следствие 2.3. Любая группа простого порядка является циклической.

Возьмем в группе, порядок которой есть простое число, какую-то ее циклическую подгруппу, образующий элемент которой отличен от единицы (нейтрального элемента) группы. Тогда эта подгруппа содержит не менее двух элементов и ее порядок, согласно теореме Лагранжа, должен быть делителем порядка группы. Поскольку порядок всей группы — простое число, а порядок подгруппы не меньше 2, то он совпадет с порядком всей группы.

Замечание. Группа, порядок которой не является простым числом, может быть циклической, т.е. утверждение, обратное следствию 2.3, не имеет места. Так, например, циклической является — аддитивная группа вычетов по модулю 4. Ее образующий элемент — 1. Можно доказать, например, что любая группа порядка 15 является циклической.

Группу называют неразложимой, если она не имеет нетривиальных подгрупп.

Следствие 2.4. Конечная группа неразложима тогда и только тогда, когда она является циклической группой, порядок которой есть простое число.

Если группа циклическая и ее порядок — простое число, то, согласно теореме Лагранжа, каждая ее подгруппа имеет порядок, равный либо единице, либо порядку всей группы, и группа неразложима.

Малая теорема Ферма

Порядок группы равен 16, следовательно, порядок циклической подгруппы, порожденной элементом а, может составлять, согласно теореме Лагранжа, 2, 4, 8, 16 (т.е. быть каким-то из делителей числа 16). Поэтому при поиске обратного элемента достаточно проверить следующие степени (кроме 15-й): 1 (остаток от деления 15 на 2), 3 (остаток от деления 15 на 4) и 7 (остаток от деления 15 на 8).

Источник