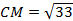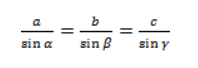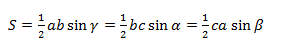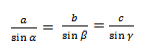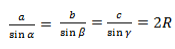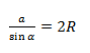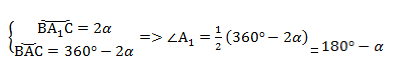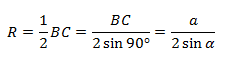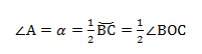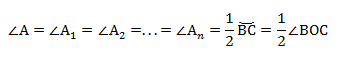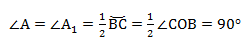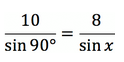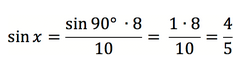Для чего нужна теорема синусов
Теорема синусов. Доказательство теоремы синусов.
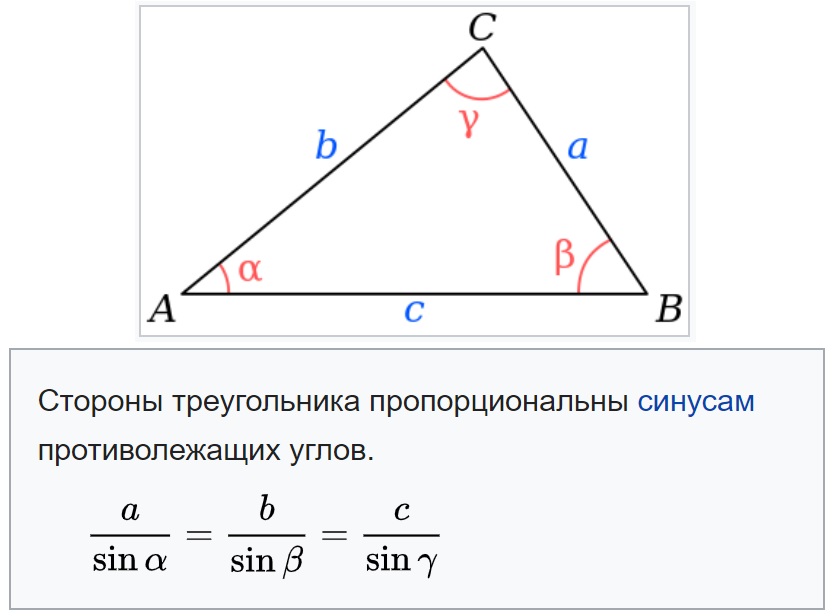
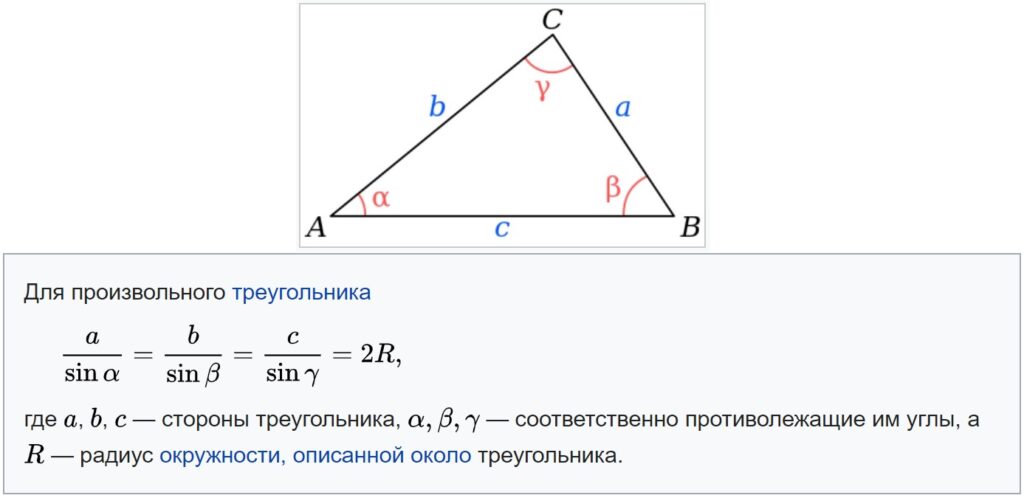
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
Есть 2 подвида теоремы: обычная и расширенная теорема синусов.
Обычная теорема синусов:
Стороны треугольника пропорциональны sin противоположных углов.
Расширенная теорема синусов для произвольного треугольника:
где a, b, c — стороны треугольника, 
Доказательство теоремы синусов.
Пусть есть треугольник, вписанный в окружность. Обозначим его как ABC.
Что бы доказать всю теорему, так как треугольник имеет произвольные размеры, можно доказать только то, что соотношение 1-ной произвольной стороны к противолежащему углу соответствует 2R. Допустим, это будет 2R = a/sin 
Проведем диаметр |BG| для описанной окружности. Из свойства углов, которые вписаны в окружность, угол GCB будет прямым, а угол CGB равен либо 





a=2R sin
Повторяем это же рассуждение для оставшихся сторон треугольника:
Теорема косинусов и синусов
Формулировка и доказательство теоремы косинусов
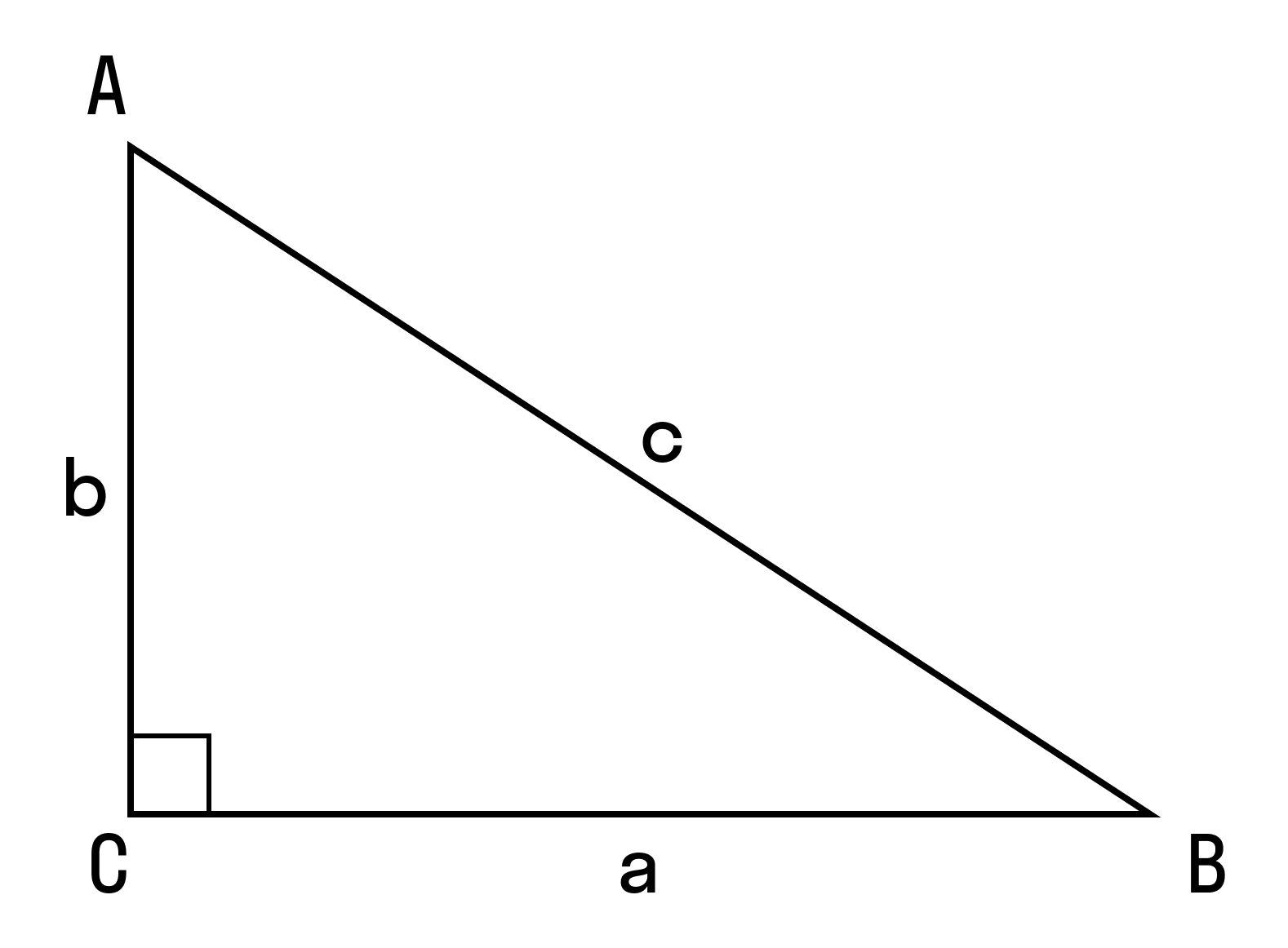
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
Приравниваем правые части уравнений:
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
Расширенная синусов теорема с примерами
При подготовке к ЕГЭ по математике одиннадцатиклассник должен помнить базовый набор формул, которые помогут решать задачи. Одной из них является синусов теорема, которая отражает взаимосвязь между сторонами и углами треугольника. Напомним, доказательство теоремы учить не нужно, поскольку экзамен ориентирован на проверку практических навыков. Лучше посвятить время разбору примеров, в которых можно применить указанную математическую закономерность.
Теорема синусов с примерами
Человечество знакомо с теоремой синусов довольно давно — еще в начале XXI века ее доказательство приводил в своей работе «Книга о неизвестных дугах сферы» западноарабский астроном и математик Ибн Муаз аль-Джайяни.
Существует два варианта теоремы синусов:
Формулировка обычной синусов теоремы: отношение сторон треугольника к синусам противолежащих углов равны или стороны пропорциональны синусам противолежащих углов.
Синусов теорема с примерами
Пример 1. В треугольнике АВС сторона АВ равна 5 см, а синус противолежащего угла АСВ = 3/5. Найти сторону ВС, если синус угла САВ, прилежащего к стороне АВ, равен 1/2.
Решение
Составим соотношение фигурирующих в условии сторон и синусов их углов:
АВ : sin ∠АСВ = ВС : sin ∠САВ.
Подставим известные значения:
Выразим из этого выражения ВС:
ВС = (5 : 3/5) : 1/2 = 5 : 1/2 = 10 см.
Ответ: ВС = 10 см.
Пример 2. В треугольнике АВС сторона АВ равна 10 см, а противолежащий угол АСВ = 30°. Найти остальные стороны, если угол САВ равен 60°.
Решение
Для решения этой задачи воспользуемся прилагаемой таблицей, в которой указаны значения синусов основных углов. В остальном ход решения будет аналогичен предыдущему примеру за исключением одного маленького хода. Для начала составим соотношение сторон и синусов противолежащих углов:
АВ : sin ∠АСВ = ВС : sin ∠САВ = АС : sin ∠ВАС.
На первом этапе нам известны только три из шести членов этого равенства, причем два из них в косвенном виде:
10 : sin 30° = ВС : sin 60° = АС : sin ∠ВАС.
Если вспомнить, что сумма углов треугольника равна 180°, то легко найти оставшийся угол:
∠ВАС = 180° – (∠АСВ + ∠САВ) = 180° – (30° + 60°) = 90°.
Мы уже знаем и третий угол, поэтому уравнение приобретет следующий вид:
10 : sin 30° = ВС : sin 60° = АС : sin 90°.
Дальше поступаем, как в предыдущей задаче, выразив стороны через известные члены выражений:
ВС = sin 60° ∙ 10 : sin 30°,
АС = sin 90° ∙ 10 : sin 30°.
Обратимся к таблице, приведенной выше и выберем из нее соответствующие синусы известных углов:
ВС = √3/2∙ 10 : 1/2 = 10√3 см,
АС = 1 ∙ 10 : 1/2 = 20 см.
Ответ: ВС = 10√3 см; АС = 20 см.
Синусов теорема с примерами
Расширенная синусов теорема с примерами
Формулировка расширенной теоремы синусов: отношение сторон треугольника к синусам противолежащих углов равны друг другу и удвоенному радиусу окружности, описанной вокруг него.
Пример 3. Найти площадь треугольника, если диаметр описанной окружности D равен 20 см. Угол АСВ = 30°, а угол САВ = 60°.
Для решения воспользуемся расширенной формулировкой теоремы синусов:
АВ : sin ∠АСВ = ВС : sin ∠САВ = АС : sin ∠ВАС = 2R.
В этой формулировке нам известны два из семи компонентов и еще лва мы можем определить из базовых знаний по геометрии:
Подставим в исходное выражение известные величины и получим соотношение:
АВ : sin 30° = ВС : sin 60° = АС : sin 90° = 20.
Основным отличием от предыдущей задачи является то, что нам неизвестна сторона АВ, зато известен удвоенный радиус описанной окружности. Это позволяет составить выражения для нахождения всех сторон треугольника:
Выберем из таблицы значения синусов углов и вычитаем стороны треугольника:
ВС = 20 ∙ sin 60° = 20 ∙ √3/2 = 10√3 см,
АС = 20 ∙ sin 90° = 20 ∙ 1 = 20 см,
АВ = 20 ∙ sin 30° = 20 ∙ 1/2 = 10 см.
Синусов теорема с примерами
Внимательный читатель заметил, что мы «зашифровали» в этой задаче треугольник из предыдущего примера. Теперь осталось найти его площадь. Для этого берем стандартную формулу площади произвольного треугольника, которая равна половине произведения сторон на синус угла между ними
Поскольку нам известны все стороны и все углы, то мы можем выбрать любые из них. Возьмем стороны АС и АВ, а также угол САВ между ними:
Примечание: внимательный читатель заметил, что наш треугольник — прямоугольный, так как один из его углов равен 90°. В таком случае можно обойтись без знания синуса угла, вычислив площадь треугольника как половину площади прямоугольника, длина и ширина которого равна катетам треугольника.
Теорема синусов (ЕГЭ 2022)
Существуют две теоремы, свзанные с тригонометрией, которые могут оказать тебе огромную услугу в решении задач — теорема синусов и теорема косинусов.
Особенно в решении задач продвинутого уровня, за которые можно получит неплохие баллы на экзамене!
О теореме косинусов можешь прочитать пройдя по ссылке, а здесь мы поговорим про теорему синусов. Легкую и полезную.
Теорема синусов — коротко о главном
Для любого \( \displaystyle \Delta ABC\):
(здесь \( \displaystyle R\) – радиус описанной окружности)
Теорема синусов — подробнее
Что же нам сообщает теорема синусов? Вероятнее всего, что-нибудь о синусах, не правда ли? Давай сформулируем.
Первый вопрос, который возникает при взгляде на эту формулу: «Но при чём же здесь вообще \( \displaystyle R\)?».
Вот давай именно с него и начнём.
Теорема синусов. Доказательство
Тебе уже известно, что около каждого треугольника можно описать окружность. Мы это и сделаем. А потом проведём диаметр \( \displaystyle BO\).
Пусть этот диаметр пересекает окружность в точке \( \displaystyle K\). Давай рассмотрим \( \displaystyle \Delta BKC\).
Что же это за треугольник?
Ну, конечно же, прямоугольный, ведь в \( \displaystyle \Delta BKC\) угол \( \displaystyle C\) опирается на диаметр \( \displaystyle BK\quad\Rightarrow \quad\angle C=90<>^\circ \) (вспоминаем тему «Вписанный и центральный угол окружности»).
Но и кроме того, \( \displaystyle \angle K\) в \( \displaystyle \Delta BKC\) равен \( \displaystyle \angle A\) в \( \displaystyle \Delta ABC\), потому что эти углы опираются на одну дугу \( \displaystyle BC\) (опять вспоминаем ту же тему).
А теперь просто запишем выражение для синуса \( \displaystyle \angle K\) в прямоугольном \( \displaystyle \Delta BKC\) \( \displaystyle \sin \angle K=\frac
Но ведь \( \displaystyle BK\) – диаметр \( \displaystyle \quad\Rightarrow\quad BK=2R\), и \( \displaystyle \sin \angle K=\frac<2R>\).
Вспомним, что \( \displaystyle \angle K=\angle A\) и получим \( \displaystyle \sin \angle A=\frac<2R>\quad\Rightarrow\quad \frac<\sin \angle A>=2R\).
Вот и всё! Провели одну линию, рассмотрели один прямоугольный треугольник – и доказательство готово.
Но как же быть с углами \( \displaystyle B\) и \( \displaystyle C\)? – спросишь ты.
Да, точно также. Давай рассмотрим \( \displaystyle \angle B\).
Теперь проведём диаметр \( \displaystyle AO\) и соединим точки \( \displaystyle K\) и \( \displaystyle C\).
Как-то тут немного по-другому получается, ты заметил? \( \displaystyle \Delta AKC\), конечно, прямоугольный, так как \( \displaystyle \angle C\) опирается на диаметр \( \displaystyle AK\).
Но теперь \( \displaystyle \angle K+\angle B=180<>^\circ \), потому что четырехугольник \( \displaystyle ABCK\) – вписанный. (Надеюсь, ты ещё помнишь, что для угла \( \displaystyle A\) у нас было \( \displaystyle \angle A=\angle K\).) В чём же дело?
Ну, просто \( \displaystyle \angle B\) – тупой, поэтому и получилось такое различие. Но, к счастью, для теоремы синусов это различие не играет роли. Сейчас мы в этом убедимся.
Итак, запишем выражение для синуса \( \displaystyle \angle K\) в прямоугольном \( \displaystyle \Delta AKC\).
\( \displaystyle \sin \angle K=\frac
Значит, \( \displaystyle \sin \angle B=\frac<2R>\quad\Rightarrow\quad \frac<\sin \angle B>=2R\).
Ну вот, мы рассмотрели и острый, и тупой угол. Если ты все ещё беспокоишься об угле \( \displaystyle C\), то проделай все те же действия самостоятельно и убедись, что все получается.
Обрати внимание, что мы доказали «четверное равенство».
в такой последовательности:
А теперь внимание! Обсудим пользу этой теоремы
Понимаешь, теорема синусов – единственный разумный способ для нахождения радиуса описанной окружности.
Почему я так говорю? А ты вспомни сам: ну где ещё в формулах участвует \( \displaystyle R\)?! Возможно, правда, ты знаком с формулой \( \displaystyle S=\frac
Из теоремы синусов: \( \displaystyle R=\frac<2\sin \angle A>\)
Из формулы площади: \( \displaystyle R=\frac
Чувствуешь разницу? В первой формуле нужно знать только одну сторону и один угол, а во второй формуле – все стороны, да ещё и площадь! Ну и какую формулу легче применить?
А кроме того, открою тебе маленький секрет: формула \( \displaystyle S=\frac
Итак, теорема синусов бывает полезна и для нахождения синуса какого – то угла, если известны две стороны и один угол.
Но в основном теорема синусов – главный инструмент для нахождения радиуса описанной окружности.
Запомни это очень хорошо!
Бонус: Вебинар из нашего курса подготовки к ЕГЭ
ЕГЭ 6, 14, 16. Теорема косинусов и синусов
Универсальный инструмент при решении треугольников — это теоремы косинусов и синусов.
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.
Теорема синусов
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Доказательство теоремы синусов
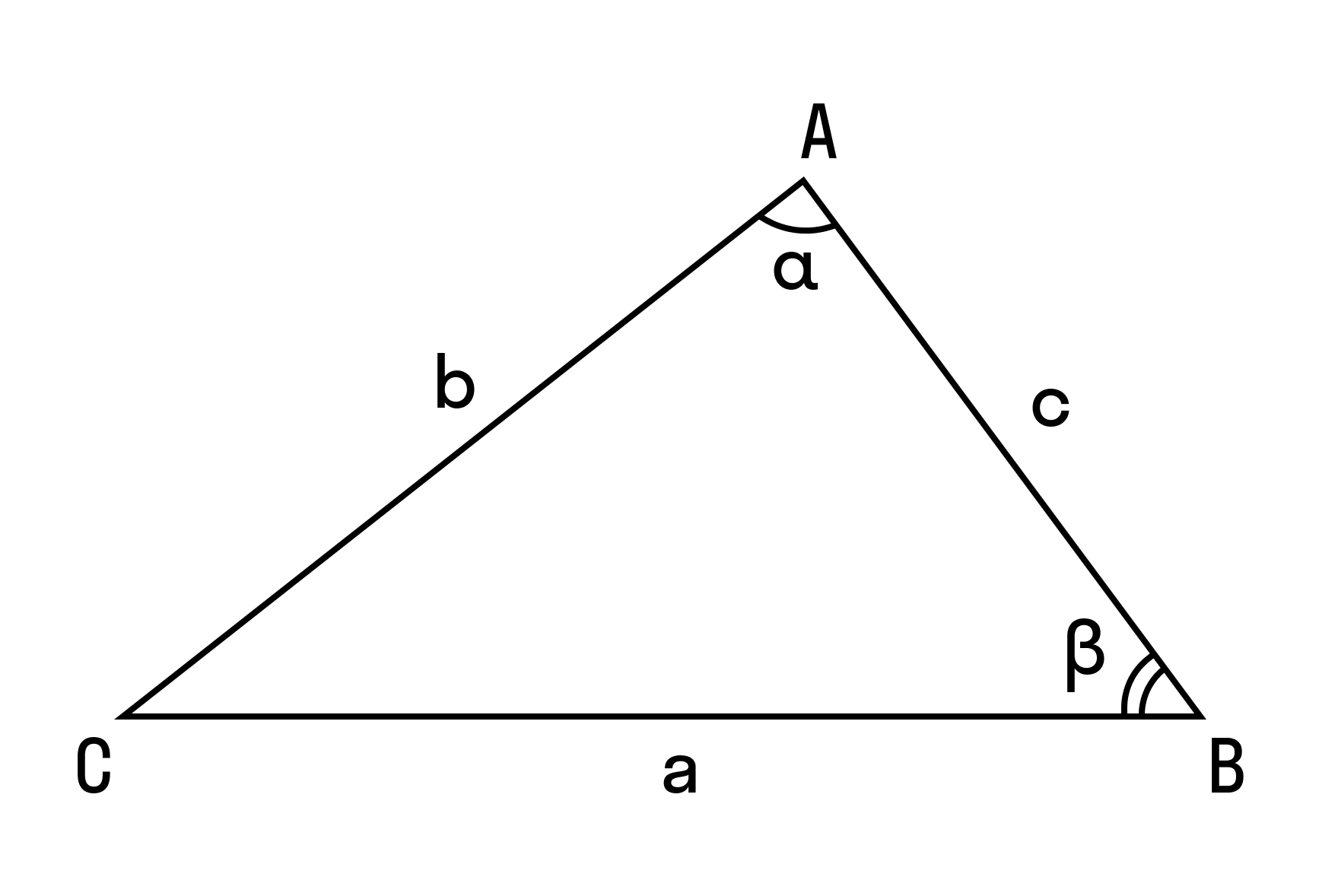
Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.
Нарисуем стандартный треугольник и запишем теорему формулой:
Формула теоремы синусов:
Докажем теорему с помощью формулы площади треугольника через синус его угла.
Из этой формулы мы получаем два соотношения:
Из этих двух соотношений получаем:
Теорема синусов для треугольника доказана.
Эта теорема пригодится, чтобы найти:
Доказательство следствия из теоремы синусов
У теоремы синусов есть важное следствие. Нарисуем треугольник, опишем вокруг него окружность и рассмотрим следствие через радиус.
где R — радиус описанной около треугольника окружности.
Так образовались три формулы радиуса описанной окружности:
Основной смысл следствия из теоремы синусов заключен в этой формуле:
Радиус описанной окружности не зависит от углов α, β, γ. Удвоенный радиус описанной окружности равен отношению стороны треугольника к синусу противолежащего угла.
Для доказательства следствия теоремы синусов рассмотрим три случая.
1. Угол ∠А = α — острый в треугольнике АВС.
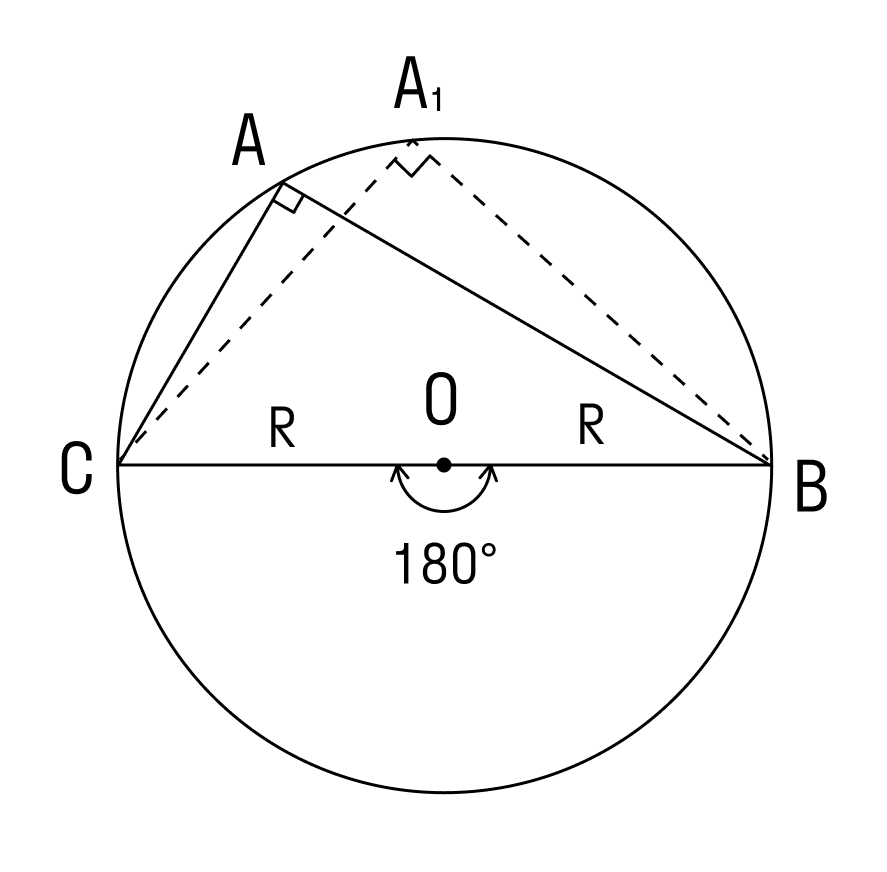
Проведем диаметр BA1. В этом случае точка А и точка А1 лежат в одной полуплоскости от прямой ВС.
Используем теорему о вписанном угле и видим, что ∠А = ∠А1 = α. Треугольник BA1C — прямоугольный, в нём ∠ BCA1 = 90°, так как он опирается на диаметр BA1.
Чтобы найти катет a в треугольнике BA1C, нужно умножить гипотенузу BA1 на синус противолежащего угла.
BA1 = 2R, где R — радиус окружности
Следовательно: R = α/2 sinα
Для острого треугольника с описанной окружностью теорема доказана.
2. Угол ∠А = α — тупой в треугольнике АВС.
Проведем диаметр окружности BA1. Точки А и A1 по разные стороны от прямой ВС. Четырёхугольник ACA1B вписан в окружность, и его основное свойство в том, что сумма противолежащих углов равна 180°.
Вспомним свойство вписанного в окружность четырёхугольника:
В треугольнике BCA1 угол при вершине С равен 90°, потому что он опирается на диаметр. Следовательно, катет а мы находим таким образом:
Следовательно: R = α/2 sinα
Для тупого треугольника с описанной окружностью теорема доказана.
Часто используемые тупые углы:
3. Угол ∠А = 90°.
В прямоугольнике АВС угол А прямой, а противоположная сторона BC = α = 2R, где R — это радиус описанной окружности.
Для прямоугольного треугольника с описанной окружностью теорема доказана.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Теорема о вписанном в окружность угле
Из теоремы синусов и ее следствия можно сделать любопытный вывод: если известна одна сторона треугольника и синус противолежащего угла — можно найти и радиус описанной окружности. Но треугольник не задаётся только этими величинами. Это значит, что если треугольник еще не задан, найти радиус описанной окружности возможно.
Раскроем эту тему на примере теоремы о вписанном в окружность угле и следствиях из нее.
Теорема о вписанном угле: вписанный в окружность угол измеряется половиной дуги, на которую он опирается.
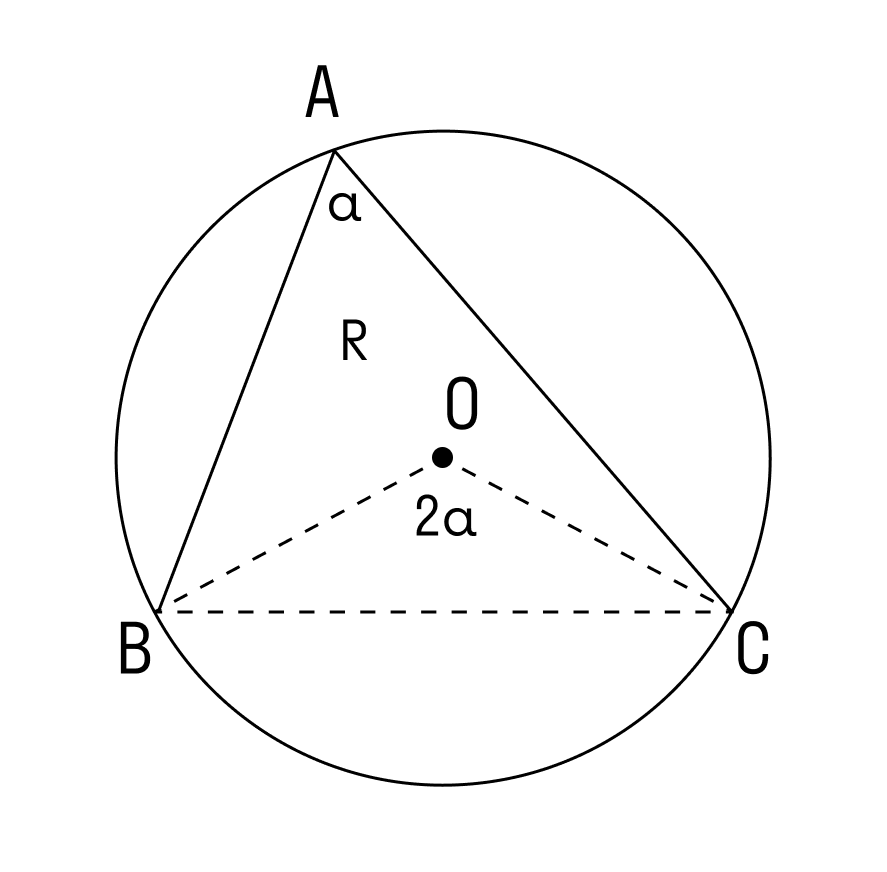
∠А = α опирается на дугу ВС. Дуга ВС содержит столько же градусов, сколько ее центральный угол ∠BOC.
Формула теоремы о вписанном угле:
Следствие 1 из теоремы о вписанном в окружность угле
Вписанные углы, опирающиеся на одну дугу, равны.
∠А = ∠BAC опирается на дугу ВС. Поэтому ∠A = 1/2(∠COB).
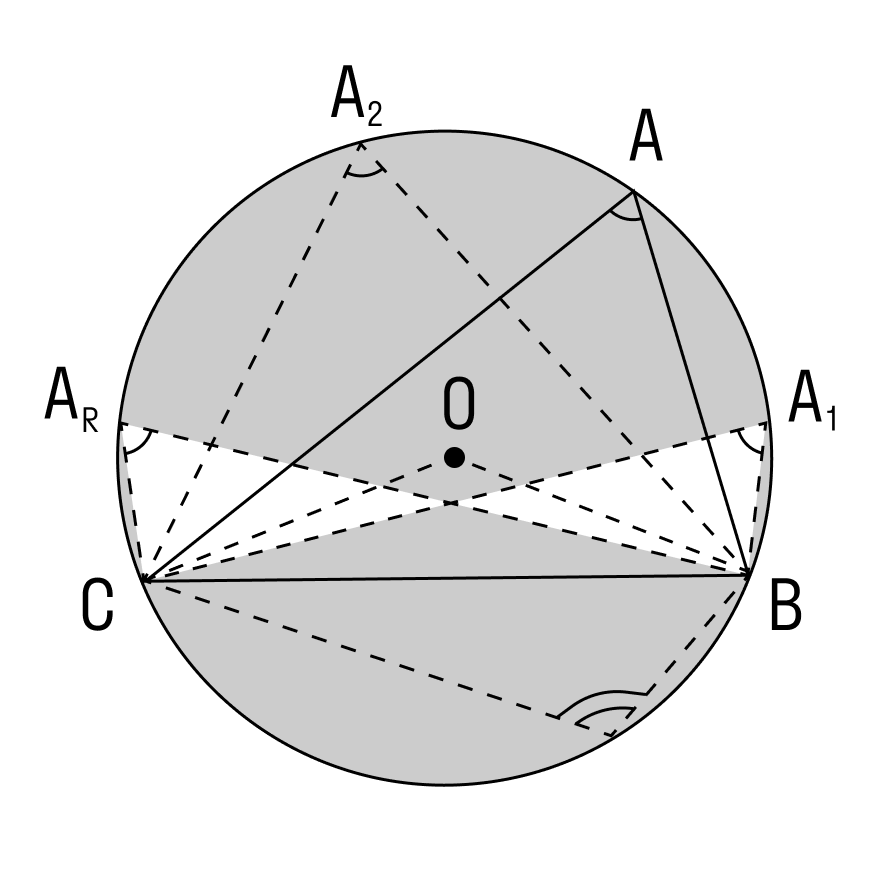
Если мы возьмём точки A1, А2. Аn и проведём от них лучи, которые опираются на одну и ту же дугу, то получим:
На рисунке изображено множество треугольников, у которых есть общая сторона СВ и одинаковый противолежащий угол. Треугольники являются подобными, и их объединяет одинаковый радиус описанной окружности.
Следствие 2 из теоремы о вписанном в окружность угле
Вписанные углы, которые опираются на диаметр, равны 90°, то есть прямые.
ВС — диаметр описанной окружности, следовательно ∠COB = 180°.
Следствие 3 из теоремы о вписанном в окружность угле
Сумма противоположных углов вписанного в окружность четырёхугольника равна 180°. Это значит, что:
Угол ∠А = α опирается на дугу DCB. Поэтому DCB = 2α по теореме о вписанном угле.
Угол ∠С = γ опирается на дугу DAB. Поэтому DAB = 2γ.
Но так как 2α и 2γ — это вся окружность, то 2α + 2γ = 360°.
Следовательно: α + γ = 180°.
Следствие 4 из теоремы о вписанном в окружность угле
Синусы противоположных углов вписанного четырехугольника равны. То есть:
Примеры решения задач
Теорема синусов и следствия из неё активно используются при решении задач. Рассмотрим несколько примеров, чтобы закрепить материал.
Пример 1. В треугольнике ABC ∠A = 45°,∠C = 15°, BC = 4√6. Найти AC.
Пример 2. Гипотенуза и один из катетов прямоугольного треугольника равны 10 и 8 см. Найти угол, который расположен напротив данного катета.
В этой статье мы узнали, что в прямоугольном треугольнике напротив гипотенузы располагается угол, равный 90°. Примем неизвестный угол за x. Тогда соотношение сторон выглядит так:
Значит x = sin (4/5) ≈ 53,1°.
Ответ: угол составляет примерно 53,1°.
Запоминаем
Обычная теорема: стороны треугольника пропорциональны синусам противолежащих углов.
>