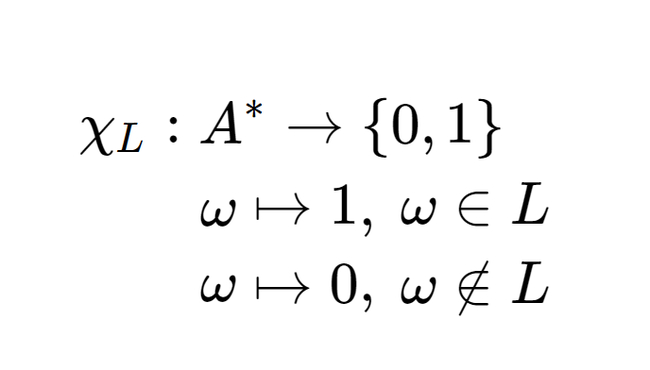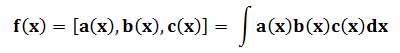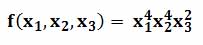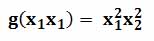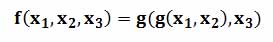Для чего нужна теория групп
Теория групп
Алексей Савватеев
Алексей Савватеев о курсе лекций:
Приглашаю вас на свой миникурс по теории групп, который я назвал «Школьная теория групп».
Я считаю, что теорию групп нужно изучать в средних классах — примерно тогда же, когда вводится символьное обозначение (буквы x,y,z и т.п.) Потому что ступень абстракции, ведущая к общему понятию группы от систем остатков по данному модулю (с одной стороны) и перестановок (с другой), не выше, чем ступень абстракции от чисел 3,4,5 к символам. Перестановки же легко понять и освоить уже во втором-третьем классе, точно так же, как и системы остатков по данному модулю.
В миникурсе я ликвидирую пробелы школьного образования, относящиеся к теории групп и к конкретным примерам групп. Будут установлены базовые факты про вычеты, доказана малая теорема Ферма, исследованы подгруппы групп перестановок на трёх и четырёх символах, введено понятие нормальной подгруппы данной группы и простоты группы.
Затем будет доказано, что группа чётных перестановок на n≥5 символах — простая (что откроет желающим дорогу к вопросам о разрешимости алгебраических уравнений в радикалах), а также что подгруппа переносов плоскости (пространства) — нормальная в группе всех (аффинных) движений соответствующего объекта. Маломерные группы движений получат полную характеризацию (теорема Шаля и законы композиции движений разных видов).
Алексей Владимирович Савватеев — доктор физико-математических наук, специалист в области теории игр, ректор Университета Дмитрия Пожарского, популяризатор математики среди детей и взрослых. Работает одновременно в нескольких научных учреждениях, в том числе в Лаборатории исследования социальных отношений и многообразия общества РЭШ. Читает в Яндексе лекции в Школе Анализа Данных, участвует в теоретических исследованиях. В Иркутске на 0.2 ставки работает доцентом ИГУ.
Матфак ИГУ (Бульвар Гагарина, 20)
5,6,9 и 10 ноября 2015 года.
Теория групп (много скукоты на ночь глядя)
Некто вдохновил меня на создание этого поста.
Сегодня мы немного коснемся теории групп. Об этой теории я узнал дай бог год назад на парах в универе. Мой извращенный всяким матаном и прочими диффурами мозг увидел нечто простое, как дверь, и красивое, как. дверь (литературным талантом я, увы, не обладаю, поэтому на эпитеты слаб). Ладно, давайте уж к делу.
Пусть у нас есть куча однотипных, но разных объектов (например, автопарк уникальных автомобилей). Обзовем его «А». Каждую отдельную машину из этого Автопарка будем обзывать маленькой буквой «а» (за которой, вообще говоря, может скрываться и Порш, и Роллс-Ройс, и, прости господи, Жигули). Так мы плавно и нежно подошли к понятию #множество.
1. Неспроста под номером один наличие в множестве #единицы (обозначим ее «E»). Но не единицы в смысле единицы (ШТА?), а единицы в смысле элемента, который в сочетании с любым другим элементом дает тот же самый элемент (а*1 = а, а+0 = a и т.д). Это как тот самый слабый игрок в команде, который всегда шарится где-то в поле и нихрена не делает.
2. Существует обратный элемент (причем единственный). То есть каждому игроку в команде соответствует чудак-антипод, который сводит всю эффективность на нет. Говоря формально, если «b» обратный «a», то a + b = E (и плюс здесь вовсе не сложение а какая-то там операция)
Итак, теперь мы знаем, что такое #группа. Но зачем? Зачем вся эта простыня текста? Зачем на вообще знать что это такое?
Разумные вопросы, поэтому свой рассказ я закончу простым примером, где эта молодая теория поставила жирную завершающую точку.
А теория групп, бесердечная сс. а, строго доказала, что формулы для корней уравнения степени больше пяти нет, как ты не старайся её отыскать (Кардано и Виет рыдают, обнявшись).
Вот как-то так. Если остаются вопросы, их можно задать в комментах.
Спасибо автору, подобные описания всегда побуждают открыть учебник, вернуться к статье понять, что написано и возрадоваться, что понял и содержимое учебника и то, что написал автор)
Чувак, я как ни разу не математик, оч благодарна за внятный ответ. Потому что по запросу «что такое теория групп» интернет выдаёт древние заклинания.
История проблемы равенства классов P и NP
В 2000 году Математический институт Клэя определил 7 математических задач, решение которых не могли найти в течение многих лет. За решение каждой из них была назначена награда в размере 1 миллиона долларов. Эти 7 задач известны как «задачи тысячелетия», и на сегодняшний день только одна из них была решена — гипотеза Пуанкаре. В этой статье пойдет речь о вопросе равенства классов P и NP, ответ на который может сильно повлиять на всю IT-сферу.
Равенство P и NP классов отсылает нас к теории алгоритмов, а именно к классам сложности. Первое, с чего стоит начать, это то, что классы P и NP классифицируют языки, а не задачи. Пока что это звучит довольно абсурдно, поэтому для понимания разберемся в некоторых деталях.
Пусть А — алфавит и L ⊆ А*, тогда L называется языком над А. Для любого алфавита пустое множество и А* являются тривиальными языками. При этом пустое множество часто называют пустым языком. Однако не стоит путать пустой язык и язык, содержащий пустое слово e, — они различны. Языки могут быть как бесконечными, так и нет, но обязательно счетными. Т. е. множество всех действительных чисел языком нельзя назвать, т. к. такой набор является неисчисляемым.
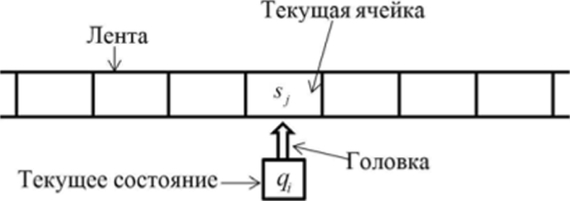
Говоря про абстрактный исполнитель, чаще всего имеют в виду машину Тьюринга, поэтому в дальнейшем под АИ будем подразумевать именно её. Итак, машина Тьюринга имеет неограниченное линейное хранилище, сгруппированное в ячейки. Каждая ячейка может содержать ровно один символ алфавита в любой момент времени. Вдоль ячеек идет считывающая головка, имеющая конечное число состояний. За одну итерацию она может считать значение только одной ячейки, переписать её значение, изменить свое состояние и перейти на одну позицию вправо/влево.
Устройство машины Тьюринга
На основе машины Тьюринга определим так называемую разрешающую машину над языком. Для начала введем определение характеризующей функции X(w). Функция X определяет, принадлежит ли слово w языку L. Если да, то значение функции равно «1»; если нет, то «0». Формально это можно записать так:
Разрешающей машиной D для языка L называется такая машина, которая для каждого w∈A вычисляет характеризующую функцию X(w) за конечное время.
В дополнение к разрешающей машине идет верификатор. Машина V, которая принимает слова w и c и выводит 0 или 1 после конечного числа шагов, называется верификатором для L, если она обладает следующими свойствами:
— выводит 1, только если w входит в язык L;
— для любого w в языке L существует такое c, что V(w,c) = 1.
Классы сложности и формулировка проблемы
Окей, мы рассмотрели несколько понятий. На первый взгляд, все это больше походит на лингвистику: алфавиты, слова, языки… Причем тут задачи? Чтобы ответить на этот вопрос, обратимся к понятию задача разрешимости (англ. Decision problem). Это такой вопрос (сформулированный в формальной системе), требующий ответа «да» или «нет», зависящего, возможно, от значений некоторых входных параметров. Например, «является ли данное натуральное число x простым?» или «даны два числа: x и y; делится ли x на y?« Метод решения в виде алгоритма называется разрешающей процедурой. Теория вычислимости имеет дело в основном с задачами разрешимости и приведенные выше конструкции наглядно соотносятся с таким типом задач: так разрешающая машина над языком является формализацией разрешающей процедуры. Но как же быть с задачами, такими как задача коммивояжера? На них нельзя дать бинарный ответ. В таких случаях применяют приемы приведения к версии decision problem. В случае коммивояжера проблема по-новому формулируется так: «существует ли маршрут не длиннее, чем заданное значение k?»
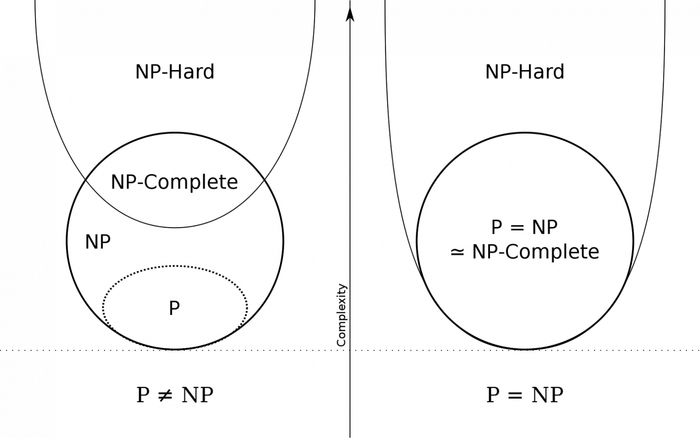
В класс сложности NP входят все языки L, для которых существует такой верификатор, что для каждого (w,c) время его работы полиномиально. Иными словами, NP включает в себя задачи разрешимости, для которых при подходящем сертификате для данного w мы быстро сможем удостовериться в том, что w действительно принадлежит L (ответ на вопрос можно довольно быстро проверить). Отсюда и название «верификатор». В качестве примера задачи в NP можно привести определение наличия в графе гамильтонова цикла. Сертификат в данном случае — последовательность вершин, образующих гамильтонов цикл.
Помимо этих классов можно выделить ещё 2: NP-hard и NP-Complete. Они основываются на приводимости одного языка к другому за полиномиальное время: пусть языки A и B — языки над одним алфавитом. Язык А будет приводимым за полиномиальное время к языку B, если существует такая функция f(w), что
— функция f может быть вычислена машиной Тьюринга за полиномиальное время.
Тогда в класс NP-hard будут входить языки, к которым приводимы все языки в NP (причем NP-hard язык может входить в NP, а может и нет), а в NP-Complete те языки, которые являются одновременно NP-hard и NP. Примером NP-Complete является язык выполнимых булевых формул (SAT). Таким образом, NP-Complete задачи образуют в некотором смысле подмножество «типовых» задач в классе NP: если для какой-то из них найден «полиномиально быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
Отношение между классами при равенстве и неравенстве
Теперь, немного погрузившись в теорию алгоритмов, более конкретно обозначим проблему равенства данных классов. Итак, множество P входит в множество NP, но неизвестно, существуют ли языки, которые входят в NP и не входят в P. Что это означает на практике? Итак, простыми словами класс NP можно охарактеризовать как «трудно решить, легко проверить». Классическим примером задачи, входящей в NP, является задача коммивояжера, для решения которой на данный момент известен лишь один алгоритм — старый добрый перебор (мы не рассматриваем эвристические методы). Однако, получив ответ, его будет не так сложно проверить. Класс P же вобрал в себя те задачи, для которых существует эффективный алгоритм решения, позволяющий решать их за полиномиальное время. И равенство или, наоборот, неравенство этих классов пока не доказано. Если эти классы равны, то это будет значить, что для всех задач, которые сейчас решаются путем перебора или другим неэффективным методом, существует(-ют) полиномиальные алгоритмы. А если не равны, то придется смириться с неоптимальностью решения этих задач.
История проблемы равенства P и NP началась в 1928 году, когда Давид Гильберт сформулировал проблему, названную Entscheidungsproblem (нем. задача разрешения). Ее суть заключается в нахождении алгоритма, определяющего доказуемость данного утверждения из аксиом с использованием правил логики. По названию очевидно, что это задача является задачей разрешения (выводит «да» или «нет»).
В ходе решения этой проблемы потребовалось определить термины «алгоритм» и «вычислимая функция». В 1936 году Алонзо Чёрч и Алан Тьюринг независимо показали, что общее решение Entscheidungsproblem невозможно, предположив, что интуитивное понятие «эффективная вычислимость» соответствует вычислимости функции на машине Тьюринга. Эта гипотеза сегодня известна как тезис Чёрча-Тьюринга.
20 марта 1956 в письме к Джону фон Нейману Курт Гёдель впервые поставил вопрос о вычислительной сложности. Гёдель интересовался, можно ли получить доказательство теоремы (в математико-логическом смысле слова) за квадратичное или линейное время. К сожалению, письмо было обнаружено лишь в 1989 году и получило широкую огласку, когда Юрис Хартманис опубликовал перевод и комментарий.
Статья Алана Кобэма 1965 года под названием «The intrinsic computational difficulty of functions» является одним из первых упоминаний класса сложности P, состоящего из разрешимых за полиномиальное время задач. Тезис Кобэма-Эдмондса (известный также как расширенный тезис Чёрча-Тьюринга), названный в честь Алана Кобэма и Джека Эдмондса, утверждает, что любая разумная модель вычислений может быть выражена через другую модель с замедлением, не более чем полиномиальным по размеру входных данных. Кобэм предположил, что класс P может быть хорошим способом для описания множества реально вычислимых задач. Любая проблема, не содержащаяся в P, невозможна, но если задача реального мира может быть решена с помощью алгоритма, существующего в P, то такой алгоритм в конечном итоге будет открыт.
В 1965 году Юрис Хартманис и Ричард Стернс опубликовали статью «On the Computational Complexity of Algorithms», отмеченную премией Тьюринга. В ней даются более точные определения сложности алгоритма и класса сложности. Хартманис и Стернс определили класс сложности как совокупность всех задач, которые можно решить за установленные временные рамки. В их статье показано, что существует бесконечная иерархия классов сложности (например, задачи, для которых наиболее быстрый алгоритм имеет время, пропорциональное n, n log n, n^2, n^3, 2^n и т. д.), где небольшое увеличение временного интервала позволяет решать больше задач. Во второй статье Хартманис совместно с Филипом М. Льюисом показали, что подобная иерархия существует и для количества памяти (функция от размера входа) при решении задачи на машине Тьюринга.
В 1967 году Мануэль Блюм разработал аксиоматическую теорию сложности, которая основана на его собственных аксиомах (аксиомы Блюма), и получил важный результат — теорему об ускорении. До этого мы говорили по большей части о сложности алгоритма. Хотелось бы аналогичным образом определить и сложность задачи: например, какова сложность самого эффективного (по времени и емкости) алгоритма, решающего эту задачу. Теорема об ускорении гласит, что есть некоторые задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм.
Точная формулировка проблемы равенства P и NP была представлена в 1971 году. Тогда американский ученый Стивен Кук и работавший независимо советский ученый Леонид Левин доказали, что существуют практически актуальные проблемы, которые являются NP-полными. В США Стивен Кук опубликовал статью «The complexity of theorem proving procedures», в которой формализовал понятия редукции за полиномиальное время и NP-полноты, а также доказал существование NP-полной задачи (задача выполнимости булевых формул, SAT). Теорема была независимо доказана Леонидом Левиным и, таким образом, получила название «теорема Кука-Левина».
В 1972 году Ричард Карп сделал рывок в знаменитой статье «Reducibility among Combinatorial Problems», в которой показал, что около 20 разнообразных задач из комбинаторики и теории графов, известных своей вычислительной трудностью, являются NP-полными.
В августе 2010 года Виней Деолаликар, работавший в исследовательском отделении Hewlett-Packard в Пало-Альто в Калифорнии, заявил, что разгадал загадку P vs NP. Он утверждал, что P не равняется NP, однако научное сообщество нашло в его доказательстве фатальную ошибку. В начале 2002 года SIGACT News провел опрос среди 100 ученых, задав им вопрос о равенстве классов NP и P. 61 человек ответили, что «неравны», 9 — «равны», 22 затруднились ответить и 8 сказали, что гипотеза не выводима из текущей системы аксиом и, таким образом, не может быть доказана или опровергнута.
К чему приведет решение проблемы
Окей, теория вычислимости, формализация алгоритмов и абстрактные математические теории — все это конечно интересно, но как решение проблемы равенства NP и P классов отразится на практике? На самом деле, алгоритмы для решения NP-задач используются каждый день во многих сферах. Например, в криптографии, криптовалютах, восстановлении поврежденных файлов, системах блокировки спама, оптимизации в логистике и т. д. Более эффективные решения могли бы значительно сэкономить время и деньги, так как мы пользуемся в основном эвристическими методами, дающими лишь приближенные решения.
Однако существует и обратная сторона монеты. Солидная часть криптографии (криптосистемы с открытым ключом, технологии доказательства выполнения работы в блокчейне, системы блокировки спама) основывается на предположении о неравенстве NP и P классов. Если окажется, что некоторые задачи, для которых, как считалось, не существует эффективных алгоритмов, можно решать быстро, то многие методы защиты устареют.
Может оказаться и так, что последствия решения окажутся не такими тривиальными, как это часто и бывает в математике. В качестве примера рассмотрим континуум-гипотезу о существовании мощности, меньшей континуума и большей мощности счетного множества. Оказывается, существование такого кардинала нельзя ни доказать, ни опровергнуть в аксиоматике ZFC. Так что мы вправе считать, что такие мощности бывают (впрочем, как и считать, что не бывают). Однако ясно, что мы не можем конструктивно построить соответствующее множество. Возможно, точно также окажется и с алгоритмами для NP-задач в случае равенства NP и P (к слову, некоторые математики в опросе SIGACT News так и ответили: гипотеза не выводима из существующей системы аксиом, то есть не может быть доказана или опровергнута).
Пока что существующих методов доказательств недостаточно для строго математического ответа, но не нужно терять надежду. В марте 2001 года Ричард Карп предсказал, что проблема будет решена молодым математиком (до 30 лет) с использованием подхода, о котором еще никто не думал. Стивен Кук заявил, что кто-нибудь предоставит убедительное доказательство в ближайшие 20 лет.
Теория групп
Математическая теория групп, это одна из центральных концепций математики. Теория групп связывает разные разделы математики в такой же степени, как и понятия числа и функции.
Здесь я попробую рассказать о теории групп как можно проще с большим количеством примеров. Сначала дам определение того, что такое математическая группа. А потом расскажу про каждый термин из этого определения.
Определение группы
Сочетание множества и операции
Таким образом, для группы нам необходимо и множество и какая-то операция между элементами этого множества. По отдельности множество без операции не может быть группой. И операция без множества тоже не может быть группой.
Например, множество всех рациональных чисел, это множество, но не группа, так как не сказано, какая операция задана на этом множестве. Точно также множествами, но не группами являются множество всех треугольников или множество всех поворотов вокруг точки в трехмерном пространстве, так как мы еще не задали операцию между элементами этого множества.
Если мы говорим просто об операциях без конкретизации множества, то это тоже не группа. Например, такие операции, как сложение или параллельный перенос не являются группой, так как не задано, с элементами каких множеств они работают.
Еще одна особенность группы заключается в том, что в качестве группы рассматривается только одно сочетание множества и операции. Например, на множестве вещественных чисел можно определить много разных операций (сложение, вычитание, умножение и т.д.). Но в группе рассматривается только одна из этих операций. Другая операция на этом же множестве может представлять собой совсем другую группу.
То же самое можно сказать и относительно операции. Например, операция сложение может быть определена и на множестве целых чисел и на множестве рациональных чисел и на множестве вещественных чисел и т.д. На каждом из этих множеств операция сложения даёт свои группы.
Множество
Множеством в математике называется любой набор любых математических объектов. Причем, совсем необязательно, чтобы эти математические объекты были однотипными.
Но, как вы понимаете, очень трудно между такими неоднородными объектами множества ввести какую-то осмысленную операцию, которая имеет хоть какое-то практическое значение и применение. Поэтому для математических групп характерны однородные множества.
Примеры однородных множеств
Это могут быть, например, множества каких-то чисел. Например, множество всех комплексных чисел, или множество всех вещественных чисел больших 6 и меньших 14, или множество всех рациональных чисел, которые делятся на 3, и т.д.
В группах могут быть множества каких-то точек пространства. Например, в качестве элементов множества можно рассматривать все возможные квадраты на плоскости, или множество всех возможных кривых в 4-мерном пространстве, или множество всех точек какого-то конкретного отрезка и т.д.
Группы бывают на множествах каких-то векторов, тензоров, матриц и т.п.
В качестве множеств могут рассматриваться какие-нибудь преобразования пространства. Например, повороты, отражения, сжатия, смещения, кручения, параллельные переносы и т.п. Причем в одном групповом множестве могут быть одновременно, например, и повороты и растяжения пространства.
В качестве множества можно рассматривать, например, множество операций перестановок. Допустим, у вас есть какие-то объекты, которые как-то различаются между собой, например, разноцветные шарики или пронумерованные шарики. И эти объекты располагаются в каком-то первоначальном порядке. Например, если это пронумерованные шарики, то они могут располагаться в ряд или в ячейках, которые образуют квадратную решетку на плоскости или кубическую в пространстве. Вы можете взять два шарика и переставить их местами. Множество таких операций по перестановки двух шариков называется множеством перестановок.
Можно придумать много разных экзотических множеств. Например, множество всех комбинаций взвешивания монет на весах или множество всех перекрашиваний граней кубика или множество всех поворотов кубика Рубика или множество всех комбинаций граней кубика Рубика и т.п.
Типы множеств
Множества бывают конечные и бесконечные. Например, множество всех натуральных чисел меньших 10 является конечным. В этом множестве только 9 элементов. (В таких странах, как Россия и Германия число 0 не считается натуральным, в отличие, например, от Франции, где 0 признается натуральным числом.) А множество всех натуральных чисел является бесконечным. Еще пример бесконечного множества, это множество всех точек круга радиуса 5 см.
Для теории групп не имеет значение, конечное множество или бесконечное. Бывают группы на конечных множествах и на бесконечных множествах.
Множества бывают дискретные и непрерывные. Например, множество всех натуральных чисел или множество всех поворотов на угол кратный 90 градусов, это примеры дискретных множеств. А примерами непрерывных множеств являются, например, множество всех точек какого-то отрезка или множество всех параллельных переносов на любое расстояние и под любым углом к какому-то направлению.
Для теории групп не имеет значение, дискретное множество или непрерывное. Бывают группы на дискретных множествах и на непрерывных множествах.
В математике в качестве множества рассматривается и пустое множество, которое ничего не содержит. Математическая группа никогда не включает в себя пустое множество, так как для пустого множества остается неопределенной групповая операция между элементами такого множества.
А вот множество из одного единственного элемента может лежать в основе группы. На таком множестве можно ввести групповую операцию.
Подмножество
Подмножество какого-то множества, это любая часть этого множества. Другими словами, каждый элемент такого подмножества в свою очередь является одновременно еще и элементом множества.
Например, целые числа, это подмножество множества рациональных чисел, так как все целые числа являются одновременно и рациональными числами. А вот множество вещественных чисел не является подмножеством множества рациональных чисел, так как к вещественным числам относятся еще и иррациональные числа, которые не являются рациональными.
Если подмножество, в свою очередь, тоже содержит какие-то свои подмножества, то эти подмножества будут тоже подмножествами множества. («Подмножество моего подмножества является моим подмножеством.») Например, целые числа в качестве подмножества содержат натуральные числа. Но целые числа, это подмножество рациональных чисел. Значит, натуральные числа тоже являются подмножеством рациональных чисел.
Выделять подмножества можно как угодно. Например, подмножеством вещественных чисел является множество всех чисел больших числа (-5) и меньших числа (+6.87). Подмножеством множества всех поворотов на плоскости вокруг точки с координатами (0,0) является множество всех поворотов на угол кратный 60 градусов.
Таким образом, если множество, например, непрерывно и бесконечно, то его подмножества могут быть тоже непрерывны и бесконечны. А могут быть и дискретными и конечными.
Каждый элемент множества является его подмножеством.
Всё множество всегда является своим подмножеством.
Пустое множество всегда является подмножеством для любого множества.
Операция
В определении группы говорится, что операция должна быть бинарной и замкнутой. Разберемся с этими терминами.
Бинарная операция
Бинарная операция, заданная на множестве, это такая операция, для проведения которой требуется два элемента множества. В группах присутствуют только бинарные операции.
Такие хорошо знакомые операции, как операции сложения, вычитания, умножения и деления на множестве вещественных чисел являются бинарными операциями, так как для их проведения нужны сразу два числа. К бинарным операциям относятся скалярное произведение векторов и векторное произведение векторов.
Если мы имеем дело с каким-то множеством преобразований пространства (повороты, отражения, сжатия, растяжения, параллельный перенос и т.п.), то бинарную операцию для такого множества преобразований можно ввести просто, как последовательное выполнение двух преобразований. Аналогично, для множества перестановок бинарную операцию можно ввести как последовательное применение двух перестановок.
Наконец, любую функцию от двух переменных можно рассматривать, как бинарную операцию.
Обращаю внимание на то, что бинарная операция подразумевает, что она может действовать не только между разными элементами множества, но и между одним и тем же элементом множества. Например, если это операция умножения на множестве чисел, то мы можем перемножать не только разные числа (типа, 3*5=15), но и одно и то же число можем умножить на само себя (типа, 4*4=16). Именно поэтому существуют группы на базе множества, состоящего только из одного элемента, хотя групповая операция бинарная.
Коммутативность бинарных операций
Обратите внимание, что в некоторых бинарных операциях мы можем переставлять местами элементы множества, и результат выполнения операции от этого никогда не меняется. А в других операциях результат от такой перестановки может измениться.
В 3-мерном пространстве, в общем случае, повороты вокруг выделенной точки не являются перестановочными. (Иначе не было бы проблемы собрать кубик Рубика.) Но если выделить какую-нибудь ось, которая проходит через эту выделенную точку, то повороты вокруг такой оси будут перестановочными. Мы сначала можем сделать, например, поворот на 30 градусов вокруг такой оси по часовой стрелке, а потом на 45 градусов против часовой стрелки. И получим точно такой же поворот, как если делать все в другом порядке: сначала сделать поворот на 45 градусов против часовой стрелки, а потом на 30 градусов по часовой стрелке.
Бинарная операция является коммутирующей (или коммутативной) или перестановочной, если её результат всегда не зависит от порядка следования в ней элементов множества, на котором эта операция определена.
Другими словами, бинарная операция коммутирующая (перестановочная) если всегда AB=BA для любых элементов A и B рассматриваемого множества. Если равенство AB=BA нарушается хотя бы в одном случае, то это некоммутирующая (неперестановочная) операция на данном множестве.
Таким образом, нельзя просто сказать, что та или иная операция коммутирующая или нет, пока не определено то множество, на котором рассматривается данная операция. Например, нельзя сказать, коммутирует или нет последовательное выполнение поворотов, пока неизвестно, где рассматриваются эти повороты, на плоскости или в 3-мерном пространстве. На плоскости повороты коммутируют друг с другом. А повороты в 3-мерном пространстве не коммутируют, так как можно привести хотя бы один пример отсутствия такой коммутации.
Коммутирует ли произведение двух матриц? Это опять зависит от того, на каком множестве матриц мы рассматриваем операцию произведения двух матриц. Если это квадратные матрицы диагонального вида, тогда произведение таких матриц всегда коммутирует. А если это любые квадратные матрицы, то произведение матриц, в общем случае, не коммутирует.
Еще примеры коммутирующих и некоммутирующих операций. Скалярное произведение векторов всегда коммутирует: (A·B) = (B·A). Векторное произведение 3-мерных векторов не коммутирует: [AxB] ≠ [BxA].
Если групповая операция перестановочная, то такие группы называются коммутирующими (или коммутативными) группами или абелевыми группами (в честь норвежского математика Нильса Хенрика Абеля, который внес большой вклад в развитие теории групп).
Унарная операция
Унарная операция, заданная на множестве, это такая операция, для проведения которой требуется только один элемент множества.
Примерами унарных операций являются такие операции, как изменение знака числа, комплексное сопряжение, транспонирование матрицы, вычисление следа матрицы, вычисление определителя матрицы, вычисление длины вектора и другие подобные операции.
На базе унарных операций группы не бывают. Единственное исключение, это когда унарную операцию можно формально рассматривать, в качестве бинарной. Такая возможность может появиться в группах на базе множества с одним элементом.
Например, рассмотрим множество, состоящее только из одной симметричной квадратной матрицы A размера nxn. В этом случае транспонирование не меняет матрицы: A T =A. Поэтому формально введем бинарную операцию, которая работает так: AA = A T = A. Такая операция на таком множестве приводит к очень простой группе.
Тернарная, кватернарная и другие n-арные операции
Кроме унарных и бинарных операций существуют операции с другими большими арностями. Их называют n-арными операциями или мультиарными. Такие операции в качестве групповых операций не используются.
Для n=3 операция называется тернарной, для n=4 будет кватернарная операция. И т.д.
Примерами тернарной операции являются функции от трех переменных: y=f(x1,x2,x3). Или, например, смешанное произведение трех трехмерных векторов: (A,B,C) = (A·[BxC]), это скалярное произведение первого вектора на векторное произведение второго и третьего вектора.
Обратите внимание, что настоящая тернарная операция (да и любая n-арная операция с n>2) не должна сводиться к последовательному применению двух (и более) однотипных бинарных операций. Если мультиарная операция сводится к комбинации нескольких однотипных бинарных операций, то группа с такой операцией может существовать, но все три правила такой группы определяются именно для той бинарной операции, к которой сводится мультиарная операция.
Например, смешанное произведение трехмерных векторов нельзя свести к двум скалярным произведениям или к двум векторным произведениям. Поэтому смешанное произведение векторов является настоящей тернарной операцией и не используется в группах. Ещё примером настоящей тернарной операции (в общем случае) является операция, определенная на множестве функций, по взятию неопределенного интеграла от произведения трех функций:
А вот пример ненастоящей, а формальной тернарной операции. Рассмотрим функцию от трех аргументов:
Если ввести бинарную функцию
Тогда тернарную функцию можно переписать как
Таким образом, эта тернарная операция свелась к двум последовательным применениям бинарной операции одного типа. Поэтому можно придумать группу, между элементами которой действует данная тернарная операция. Но все три правила групповой операции будут относиться только к бинарной операции, из которой состоит эта тернарная операция.
Замкнутая операция
Замкнутая операция, заданная между элементами множества, это такая операция, результатом которой являются элементы того же самого множества. Другими словами, применение замкнутой операции не «выбрасывает» её результат за пределы рассматриваемого множества.
Например, операция сложения для множества натуральных чисел, это замкнутая операция, так как при сложении двух натуральных чисел в результате всегда получается только натуральное число. А вот операция вычитания для множества натуральных чисел не является замкнутой, так как при вычитании большего натурального числа из меньшего получается отрицательное число, а не натуральное.
Аналогично, операция умножения на целых числах является замкнутой, так как при перемножении целых чисел всегда получается только целое число. А операция деления для множества целых чисел уже не является замкнутой, так как в результате деления целых чисел может получиться дробное число.
Векторное произведение трехмерных векторов является замкнутой операцией, так как в результате тоже получается трехмерный вектор. А вот скалярное произведение векторов, это уже не замкнутая операция, так как в результате такой операции получается не вектор, а число.
Замкнутые и незамкнутые операции бывают в операциях с любой мультиарностью.
Например, унарная операция транспонирования матрицы, это замкнутая операция, так как в результате транспонирования получается тоже матрица. А унарная операция получения определителя матрицы, это для матриц размера 2×2 и выше уже не замкнутая операция, так как в результате неё получается не матрица, а число.
Тернарная операция смешанного произведения трех трехмерных векторов не является замкнутой, так как в результате получается число, а не трехмерный вектор. А операция из предыдущего раздела, определенная для множества функций, по взятию неопределенного интеграла от произведения трех функций является замкнутой, так как в результате её тоже получается функция.
В качестве групповых операций используются только замкнутые операции.
Итак, все групповые операции, это только одновременно и замкнутые и бинарные операции.
Далее рассмотрим три обязательных групповых свойства этих групповых операций. Если эти три свойства не выполняются, то такое сочетание множества и операции на нем не является группой.
1. Ассоциативность
Свойство ассоциативности говорит о том, что для операций в группе скобки можно расставлять, как угодно (естественно, с соблюдением правила, что число открытых скобок должно быть равно числу закрытых скобок).
Например:
ABCDEFGH = (AB)(CD)(EFG)H = (ABC(DEFG))H = A(B(C(DE)F)G)H
Расстановка скобок определяется соображениями удобства. Понятно, что если скобки расставить вот так:
5677+(754-754)+(287-287)-5677,
то это выражение будет вычислено гораздо быстрее, чем, если скобки поставить, например, так:
(5677+754)+(-754+287)+(-287-5677)
2. Единичный элемент
В этом пункте определения группы нужно обратить внимание на то, что единичный (нейтральный) элемент группы всегда коммутирует с любым элементом множества: AE=EA, даже если группа некоммутативная.
Обратите внимание, что единичные элементы группы на одном и том же множестве могут быть разными для разных операций. Ведь это, по существу, разные группы. Например, для множества вещественных чисел операция сложения дает группу с единичным элементом равным 0. А операция умножения на том же множестве (без нуля, естественно) дает группу с единичным элементом равным 1.
Еще примеры единичных элементов группы. Если группу образуют матрицы размера nxm с операцией сложения матриц, то единичным элементом группы будет нулевая матрица размера nxm. Если группу образуют квадратные матрицы размера nxn с операцией умножения матриц, то единичным элементом группы будет матрица размера nxn, с единицами по диагонали и нулями во всех других местах.
Еще обратим внимание на то, что самая маленькая группа состоит только из одного элемента. И этим единственным элементом группы как раз и является единичный элемент. Именно в таких группах унарные замкнутые операции можно формально считать бинарными замкнутыми операциями. Выше был дан пример такой группы из одной симметричной матрицы с групповой операцией транспонирования матрицы.
3. Обратный элемент
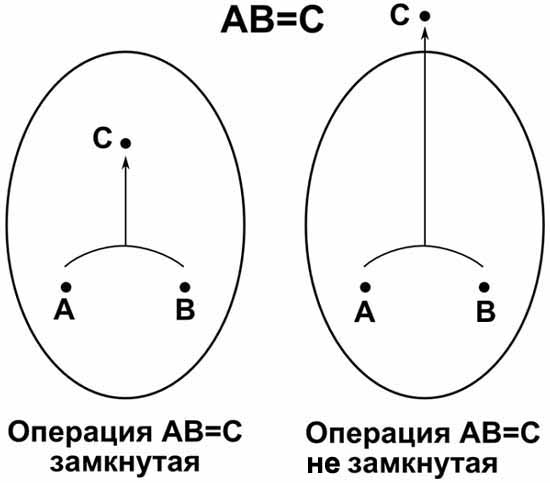
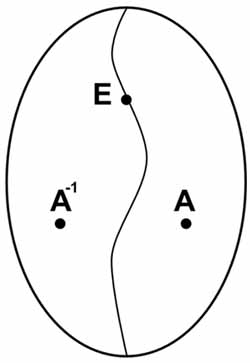
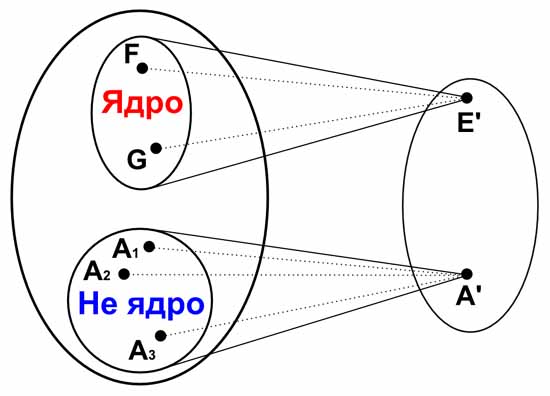
Следующее, на что надо обратить внимание, это то, что совсем необязательно, чтобы элемент группы не совпадал со своим обратным элементом. Иногда, начинающие знакомиться с теорией групп думают, что группа должна иметь такую структуру, как на рисунке. То есть, будто бы, любое групповое множество можно разделить на две части. В разных частях, будто бы, находятся элементы обратные друг другу, и есть еще один единичный элемент, который обратен самому себе в качестве исключения.
Такая ситуация действительно бывает, но не всегда. Примером того, когда бывает такая ситуация, служит группа с операцией сложения для множества целых чисел (или рациональных или вещественных чисел). В этом случае мы можем разделить множество элементов группы на три подмножества, в одном из которых будут все положительные числа, а в другом подмножестве будут все отрицательные числа. И еще будет третье подмножество, состоящее только из одного числа 0, которое является единичным элементом группы.
Такое разделение в этом примере неоднозначное. В первое подмножество мы можем включить все отрицательные числа, кроме, например, числа (-2). Вместо него включим в первое подмножество число (+2). А во второе подмножество включаем все положительные числа, кроме числа (+2), вместо которого берем число (-2).
Например, группа отражений трехмерного пространства относительно плоскости с операцией последовательного применения двух отражений. Это группа из двух элементов. Первый элемент, это единичный элемент, когда пространство не преобразуется. Второй элемент, это отражение. При отражении каждая точка пространства переходят в точку, расположенную на прямой линии, перпендикулярной плоскости, и на таком же расстоянии от плоскости, только с другой стороны этой плоскости. Если сделать два таких последовательных отражения, то точки пространства вернутся на свои первоначальные места, то есть получим единичный элемент группы. Значит, отражение является обратным элементом группы к самому себе.
Еще пример, когда обратный элемент группы совпадает со своим элементом, это группа перестановок. Если 2 раза сделать одну и ту же перестановку, то ничего не изменится.
Подгруппа
Понятие подгруппы более сложное, чем понятие подмножества. Не любое подмножество группового множества может образовать подгруппу.
В группе и в её подгруппе действует одна и та же групповая операция. Значит, чтобы выделить подгруппу из группы, надо в групповом множестве выделить такое подмножеств, чтобы это подмножество с этой операцией само образовывало самостоятельную группу.
Понятно, что раз в подгруппе действует та же самая групповая операция, то значит, в подгруппу всегда входит единичный элемент группы. Бывает, что в одной группе можно найти несколько подгрупп, но каждая из этих подгрупп обязательно будет содержать единичный элемент группы.
У каждой группы, в общем случае, всегда есть две её тривиальных подгруппы. Это подгруппа с одним единичным элементом и подгруппа, которая совпадает с самой группой. Эти две подгруппы любой группы называются несобственными или тривиальными подгруппами. Если группа состоит только из одного элемента, то у неё только одна несобственная подгруппа.
Все другие подгруппы называются собственными (нетривиальными) подгруппами. Бывают такие группы, которые содержат только тривиальные подгруппы. А бывают и такие, которые кроме тривиальных подгрупп содержат еще и собственные подгруппы.
Группы, у которых есть только тривиальные подгруппы, называются простыми группами. Это по аналогии с простыми числами. Простые числа, это такие числа, которые имеют только два своих делителя: число 1 и само себя.
Рассмотрим примеры групп, которые имеют собственные подгруппы.
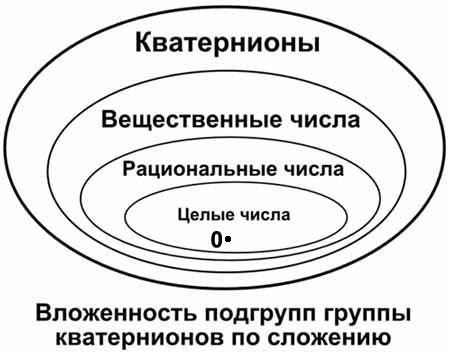
Группа для множества комплексных чисел с операцией сложения имеет в качестве подгруппы группу вещественных чисел с операцией сложения. В свою очередь группа вещественных чисел с операцией сложения имеет подгруппу в виде группы рациональных чисел. При этом группа рациональных чисел с операцией сложения является ещё и подгруппой комплексных чисел с операцией сложения. («Подгруппа моей подгруппы является моей подгруппой.»)
У группы рациональных чисел по сложению есть еще одна подгруппа, это группа целых чисел по сложению. Таким образом, группа целых чисел со сложением является ещё и подгруппой таких групп, как группа вещественных чисел и группа комплексных чисел.
А вот натуральные числа с операцией сложения уже не являются подгруппой группы целых чисел, так как множество натуральных чисел с операцией сложения не образуют группы. Операция сложения не является групповой операцией для множества натуральных чисел, так как для такого сочетания множества и операции не выполняется третье свойство группы, о существовании обратных элементов. (А в России и в Германии не выполняется ещё и второе свойство группы, так как в этих странах число 0 не считается натуральным числом.)
Если в какой-то группе есть две подгруппы, то их пересечение всегда тоже является подгруппой данной группы. А вот объединение этих подгрупп не всегда является подгруппой данной группы.
Изоморфизм и гомоморфизм
Гомоморфизм
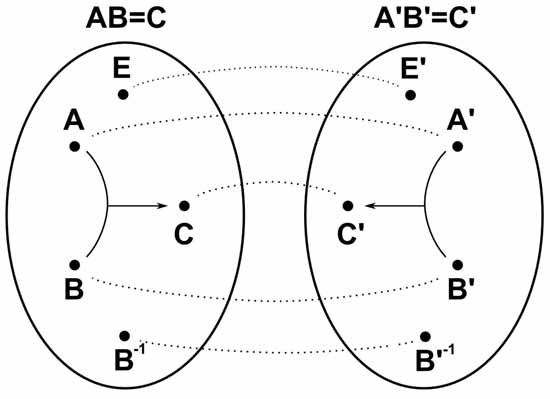
Одна группа гомоморфна другой группе, если любым двум элементам A и B из первой группы можно однозначно сопоставить два элемента A’ и B’, соответственно, из второй группы так, что если AB=C, а A’B’=C’, то элементу C из первой группы однозначно сопоставляется элемент C’ из второй группы.
Фактически, это означает, что существует какая-то однозначная операция отображения всех элементов первой группы на все элементы второй группы так, что при этом сохраняются все отношения между элементами, задаваемые групповыми операциями. Такое отображение называется гомоморфизмом.
Из этого понятно, что единичный элемент первой группы при гомоморфизме всегда соответствует единичному элементу второй группы. А все пары взаимно обратных элементов первой группы всегда соответствуют парам взаимно обратных элементов второй группы.
Простой пример гомоморфизма. Группу целых четных чисел с операцией сложения можно однозначно отобразить на группу всех целых чисел с операцией умножения. При этом числу 0 первой группы соответствует число 0 второй группы. Числу 2 первой группы соответствует число 1 второй группы. Числу 4 первой группы соответствует число 2 второй группы. И т.д. То же самое и с отрицательными числами. В общем случае число n из второй группы является соответствием числа 2n из первой группы.
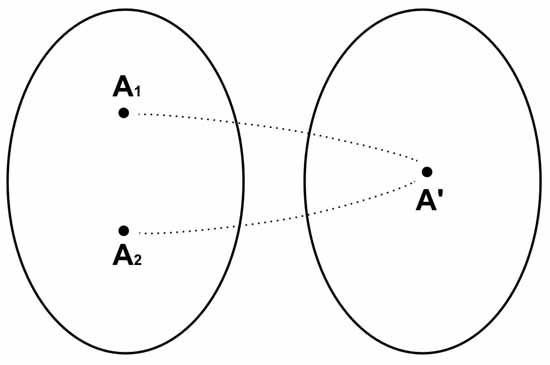
Гомоморфизм требует однозначности такого отображения, но не требует при этом взаимности этого отображения. То есть элемент A из первой группы имеет только один соответствующий ему элемент A’ из второй группы. Во второй группе нет никакого другого элемента, который соответствует элементу A из первой группы. Но вот для двух разных элементов A1 и A2 из первой группы (A1≠A2) допускается иметь только один соответствующий им элемент A’ из второй группы.
В этом смысле вторая группа может не только иметь меньше элементов, чем первая группа, но и быть более простой, чем первая группа. Ядром гомоморфизма первой группы называется такая подгруппа первой группы, которая при гомоморфизме переходит в единичный элемент второй группы.
Изоморфизм
Изоморфизм, это взаимно однозначный гомоморфизм.
То есть, когда элементу A первой группы не только соответствует один элемент A’ второй группы, но и элементу A’ соответствует только один элемент A из первой группы.
Если между двумя группами существует изоморфизм, то данные группы называются изоморфными. Изоморфные группы не отличаются друг от друга с точки зрения теории групп. С точки зрения теории групп изоморфные группы являются совершенно одинаковыми. Элементы таких групп могут иметь разную математическую природу, операции таких групп также могут быть разными, но в теории групп, это одна и та же группа.
Рассмотрим пример изоморфизма. Пусть одна группа представляет собой 4 числа, 1, i, -1, -i, где i, это мнимая единица, а групповой операцией будет умножение этих чисел. Данная группа изоморфна группе вращений плоскости, которые совмещают квадрат с самим собой при поворотах квадрата вокруг своего центра с групповой операцией последовательного применения двух вращений.
Соответствуют друг другу число 1 и поворот на 0 градусов, число i и поворот на 90 градусов, число (-1) и поворот на 180 градусов, число (-i) и поворот на 270 градусов. Можно убедиться, что операция умножения в первой группе точно соответствует операции сочетания двух соответствующих поворотов из второй группы.
Изоморфизм в теории групп полезен тем, что позволяет перенести многие доказанные математиками вещи из одной области математики в другую, когда удается доказать изоморфизм основных групп в этих разных областях математики.