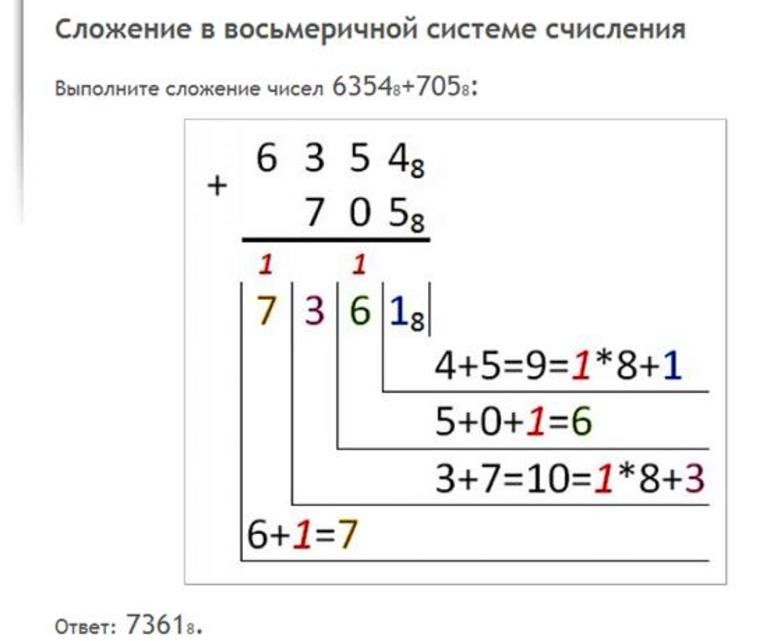
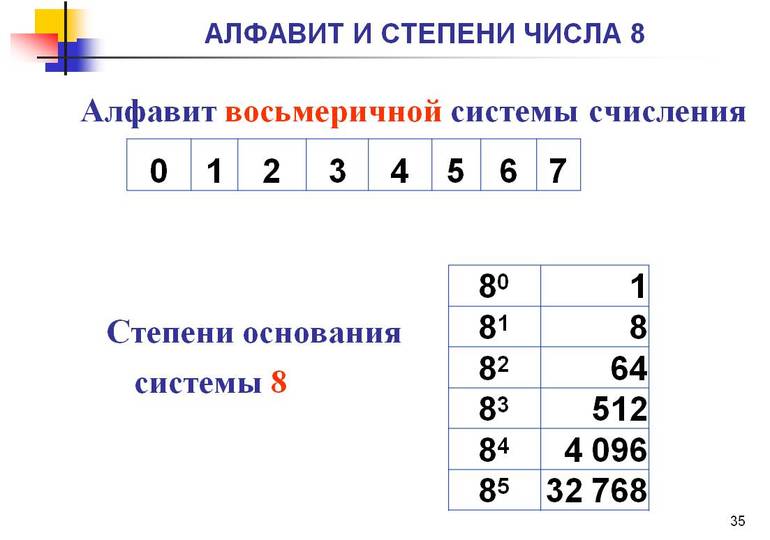
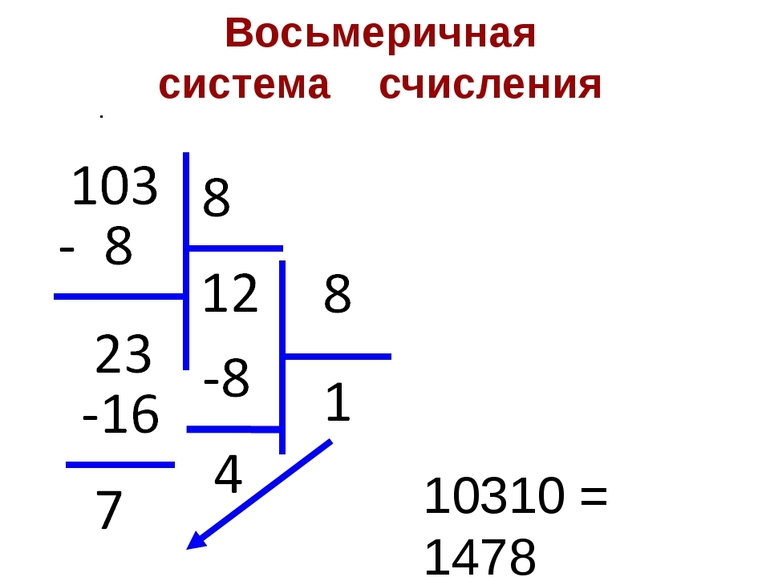
Для чего нужна восьмеричная система счисления
Восьмеричная система счисления
Из Википедии — свободной энциклопедии
| Системы счисления в культуре | |
|---|---|
| Индо-арабская | |
| Арабская Тамильская Бирманская | Кхмерская Лаосская Монгольская Тайская |
| Восточноазиатские | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные | |
| Абджадия Армянская Ариабхата Кириллическая Греческая | Грузинская Эфиопская Еврейская Акшара-санкхья |
| Другие | |
| Вавилонская Египетская Этрусская Римская Дунайская | Аттическая Кипу Майяская Эгейская Символы КППУ |
| Позиционные | |
| 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60 | |
| Нега-позиционная | |
| Симметричная | |
| Смешанные системы | |
| Фибоначчиева | |
| Непозиционные | |
| Единичная (унарная) | |
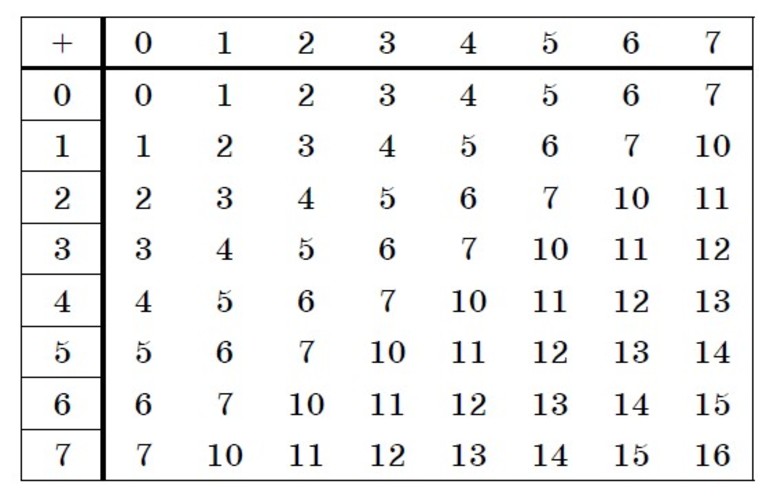
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Широко использовалась в программировании и компьютерной документации, однако позднее была почти полностью вытеснена шестнадцатеричной.
Зачем нужна восьмеричная система счисления в 21 веке?
Работа в восьмеричной системе может быть полезна в случае операций с битовыми флагами и масками по причине простоты вычисления таких значений.
Для последовательности из 3 битов очень удобно применять цифры от 0 до 7 (все цифры восьмеричной системы), а операции для вычисления восьмеричного числа очень простые.
Рассмотрим пример с установкой битов от 000 до 111:
установка правого крайнего бита (младшего) увеличит восьмеричное число на 1
установка среднего бита увеличит восьмеричное число на 2
установка старшего бита увеличит восьмеричное число на 4
То есть, нужно определить состояние каждого бита и соответствуюшее ему число, а затем просуммировать биты в состоянии 1.
Расставим биты и соответствующие им цифры, как описано выше:
Теперь когда мы устаналиваем какой-то бит, к итоговой сумме просто прибавляем соответствующую цифру.
Эта математика очень проста для вычисления в уме, именно потому и применяется в системе маркировки прав доступа к файлам в *nix.
Теперь добавим ещё немного сложности, и рассмотрим систему из 8 битов, т.е. полноценный байт.
Его можно разбить на 3 секции по битам, и я приведу соответствующие цифры восьмеричной системы:
Теперь, правило такое: в рамках 3 битов в группе числа суммируются, как раньше с 3 битами, но цифры каждой отдельной группы пишутся каждая в своём разряде.
Начнём вычисления справа налево (от младшего разряда, отсчитывая по 3 бита):
Значит, итоговое число будет 275 в восьмеричной системе. Фактически, мы отдельно работаем с каждой группой битов (по 3 бита в группе), а потом просто записываем их в нужном порядке.
То есть, если программисту нужно установить битовую последовательность 10111101, достаточно определить в коде переменную с восьмеричным значением 275
Во многих языках программирования нет специального синтаксиса для зависи двоичных значений, например в наиболее распространённых языках C и C++, и удобная запись в восьмеричной системе очень помогает.
В C/C++ и ряде других языков, например Go, восьмеричное число 275 записывается как 0275 (ноль в начале означает, что это восьмеричная система)
Приведу простейший пример на Go (его можно запустить онлайн в https://play.golang.org)
package main
import «fmt»
func main() <
bitmap := 0275 // в Go восьмеричные числа начинаются с нуля, как и в C
fmt.Printf(«%b\n», bitmap)
>
А теперь, как тот же код можно написать используя операции битового сдвига:
1 значит ставим 111
Общие сведения
Во время изобретения персонального компьютера (ПК) или ЭВМ использовался определенный язык представления данных, который существенно отличался от десятичной системы счисления. Последняя используется человеком при ведении расчетов и является самой удобной.
Кодирование данных в современных ЭВМ осуществляется за счет элементов (транзисторов) в интегральных микросхемах. За основу взят полупроводниковый переход, который может быть закрытым или открытым. Следует отметить, что режим «насыщения», присущий радиодетали, не используется. Если он открыт, то в триггер (память) записывается единица, а в противном случае — нуль. В результате этого кодирование осуществляется в двоичном коде (0 или 1), основанием которого является цифра «2».
Для кодирования больших массивов информации использовать двоичную систему счисления не всегда удобно, поскольку количество транзисторов может быть огромным, а устройство будет значительно греться. Чтобы этого избежать, была придумана восьмеричная система счисления.
Для выполнения операции конвертации десятичной системы исчисления в восьмеричный код необходимы некоторые базовые знания. К ним относятся:
Специалисты в области информационных технологий рекомендуют разбирать базовые понятия в последовательности, состоящей из пяти шагов.
Число и цифра
При расчетах и выражении количественных характеристик процесса или явления применяются определенные математические символы — числа. Они состоят из разрядной сетки. Каждый ее элемент — цифра, которая принимает значения, в зависимости от выбранной системы счисления (СС). Например, для десятичной используется диапазон от 0 до 9, а девятеричная состоит из интервала с минимальной величиной, равной 0, а максимальной — 8.
Цифра — математический знак, используемый для построения более сложных конструкций. Например, с его помощью можно записать значения различных типов (четырехзначные, пятизначные). Любое число состоит из разрядной сетки, элементами которой и являются математические символы.
При выполнении различных математических операций нужно следить за одинаковыми разрядами. Например, недопустимо складывать сотни и тысячи, поскольку это действие приведет к ошибочным вычислениям. Далее следует разобрать системы представления информации и их примеры.
Виды числовых представлений
Для правильного перевода чисел из одной СС в другую необходимо разобрать классификацию форм представления информации. Они бывают двух типов, в зависимости от расположения цифр:
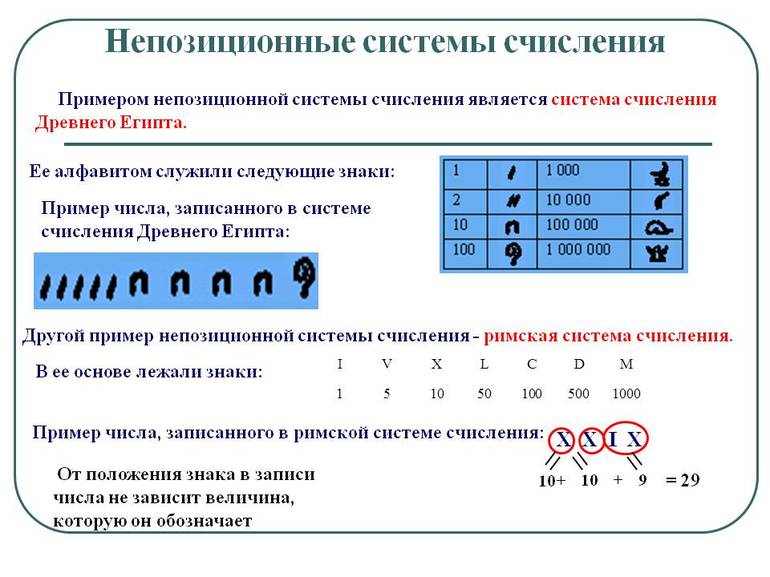
Независимыми от расположения разрядов называются непозиционные СС. Примером одной из них является унарная форма записи числа. Суть ее заключается в эквивалентности символа какому-либо значению. Например, на предприятиях применяются обыкновенные «крестики» для подсчета количества рабочих дней сотрудников. Каждый символ эквивалентен единице.
На уроках математики в начальных классах также применяется инструмент — счетные палочки. Последние помогают ученикам развивать навык устного счета и являются компонентами непозиционной СС. С их помощью возможно выполнять операции суммы, разности, а также произведения и деления.
Следует отметить, что не во всех случаях один символ может соответствовать единице. Это могут быть десятки, сотни и даже тысячи. Для расчетов при помощи непозиционной СС можно придумать собственные обозначения, как это сделано в римских цифрах. Однако при этом существуют определенные недостатки:
Достоинством считается сокращение времени записи величины, которая постоянно изменяется. Например, при подсчете количества выходов персонала достаточно поставить крестик или палочку, и это делается без исправлений. В случае с десятичной СС исправлений избежать невозможно.
Чтобы выполнить перевод в восьмеричную систему счисления, необходимо ознакомиться с методикой конвертации десятичной формы в двоичное кодовое представление.
Двоичная кодировка
Для преобразования десятичной величины в двоичную IT-специалистами были разработаны специальные правила или алгоритмы. К ним относятся столбик и степень. Каждому начинающему IT-специалисту необходимо выбрать оптимальную методику преобразования одной формы числа в другую. Каждый из способов удобен в конкретной ситуации. Можно также применять сразу 2 — один для решения, а другой — для проверки результата. Необходимо разобрать каждую методику подробно с практической реализацией алгоритма.
Метод «столбик»
Первый способ получил широкое применение, поскольку для его выполнения требуется минимум знаний в математической сфере. Он имеет следующий вид:
Реализация алгоритма проверяется на практическом примере. Для этого требуется решить задачу конвертации числа из десятичной СС в другую, перевод 167 <10>в <2>. Решение имеет следующий вид:
Обратный алгоритм конвертации из двоичной в десятичную форму представления величины основан на соответствии значений степенным показателям двойки. Разбиение на разрядную сетку осуществляется справа налево. Методика имеет такой вид:
Реализация методики проверяется на практическом примере — следует взять двоичный код из предыдущего задания, т. е. 10100111. Алгоритм нахождения десятичной формы имеет следующий вид:
Переводить системы счисления в другие формы представления возможно при помощи различных онлайн-сервисов. Для этого требуется указать исходную форму числа, а затем конечную. Однако действия рекомендуется совершать только для проверки результата решения задачи.
Способ степени
Для конвертации в двоичный код также применяется метод степени. Суть его заключается в представлении числа в виде отдельных элементов с основанием «2» и некоторым показателем. Алгоритм в этом случае выглядит таким образом:
Как и во всех остальных случаях, рекомендуется разобрать алгоритм на практическом примере. Решение задачи для числа «167» имеет такой вид:
Однако операция преобразования является вспомогательной. Она применяется для дальнейшей конвертации в восьмеричную СС.
Восьмеричная система
Восьмеричная форма представления чисел состоит из основания-восьмерки и триады. Совокупность последних образуют любые значения. Для кодирования информации в этом случае применяется меньше регистров памяти. Этого нельзя сказать о двоичном коде.
Для восьмеричного представления применяются цифры от 0 до 7 (всего 8). Многие новички часто путают ее с шестнадцатеричной СС, в которой содержатся символы латинского алфавита. При выполнении операций конвертации специалисты рекомендуют ознакомиться со списком (таблицей) восьмеричной системы:
Он поможет перевести любое числовое сообщение. Для удобства IT-специалисты рекомендуют составить презентацию или записать на лист плотной бумаги перекодировку списка. Заучивать коды нет необходимости, поскольку достаточно решать примеры (информация отложится в памяти). Алгоритм кодирования очень прост:
После ознакомления с методикой преобразования нужно проверить ее реализацию на примере. Требуется выяснить, значение 167 <10>. Это делается довольно просто:
Обратное декодирование выполняется по такой методике:
На начальных этапах обучения рекомендуется четко следовать по пунктам методики. Однако через некоторое время последние можно опускать.
Таким образом, восьмеричная система применяется для кодирования больших массивов информации, при котором может быть задействовано минимальное количество регистров запоминающего устройства персонального компьютера.
Восьмеричная система счисления
| Системы счисления в культуре | |
|---|---|
| Индо-арабская система счисления | |
| Арабская Индийские Тамильская Бирманская | Кхмерская Лаоская Монгольская Тайская |
| Восточноазиатские системы счисления | |
| Китайская Японская Сучжоу Корейская | Вьетнамская Счётные палочки |
| Алфавитные системы счисления | |
| Абджадия Армянская Ариабхата Кириллическая | Греческая Эфиопская Еврейская Катапаяди |
| Другие системы | |
| Вавилонская Египетская Этрусская Римская | Аттическая Кипу Майская |
| Позиционные системы счисления | |
| Десятичная система счисления (10) | |
| 2, 3, 4, 5, 6, 7, 8, 9, 12, 16, 20, 60 | |
| Нега-позиционная система счисления | |
| Симметричная система счисления | |
| Смешанные системы счисления | |
| Фибоначчиева система счисления | |
| Непозиционные системы счисления | |
| Единичная (унарная) система счисления | |
| Список систем счисления | |
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.
Таблица перевода восьмеричных чисел в двоичные
Для перевода восьмеричного числа в двоичное необходимо заменить каждую цифру восьмеричного числа на триплет двоичных цифр. Например: 25418 = [ 28 | 58 | 48 | 18 ] = [ 0102 | 1012 | 1002 | 0012 ] = 0101011000012
Ссылки
Полезное
Смотреть что такое «Восьмеричная система счисления» в других словарях:
Восьмеричная система счисления — позиционная система счисления с основанием 8, в которой для записи чисел используются цифры 0, 1, 2, 3, 4, 5, 6 и 7. См. также: Позиционные системы счисления Финансовый словарь Финам … Финансовый словарь
ВОСЬМЕРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ — (octal notation) Система чисел, использующая для выражения чисел восемь цифр от 0 до 7. Так, десятичное число 26 в восьмеричной системе будет записано как 32. Не будучи столь популярной, как шестнадцатиричная система счисления (hexadecimal… … Словарь бизнес-терминов
восьмеричная система счисления — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN octal notation … Справочник технического переводчика
восьмеричная система счисления — aštuonetainė sistema statusas T sritis automatika atitikmenys: angl. octal notation; octal number system; octal system; octonary notation vok. Achtersystem, n; oktales Zahlsystem, n; Oktalschreibweise, f; Oktalsystem, n rus. восьмеричная система … Automatikos terminų žodynas
восьмеричная система — aštuonetainė sistema statusas T sritis automatika atitikmenys: angl. octal notation; octal number system; octal system; octonary notation vok. Achtersystem, n; oktales Zahlsystem, n; Oktalschreibweise, f; Oktalsystem, n rus. восьмеричная система … Automatikos terminų žodynas
Система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Двенадцатиричная система счисления — Двенадцатеричная система счисления позиционная система счисления с целочисленным основанием 12. Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Существует другая система обозначения, где для недостающих цифр используют не A и B, а t от… … Википедия
Двенадцатичная система счисления — Двенадцатеричная система счисления позиционная система счисления с целочисленным основанием 12. Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Существует другая система обозначения, где для недостающих цифр используют не A и B, а t от… … Википедия
ШЕСТНАДЦАТИРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ — (hexadecimal notation) Числовая система, использующая десять цифр от 0 до 9 и буквы от A до F для выражения чисел. Например, десятичное число 26 записывается в этой системе как 1А. Числа шестидесятеричной системы широко используются в… … Словарь бизнес-терминов
Позиционная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Восьмеричная система счисления — правила и примеры решений
Для обеспечения интерфейса «пользователь-компьютер» необходимо переводить числа из одной формы представления в другую. В этом случае может быть полезна восьмеричная система счисления, позволяющая представлять любую информацию в некотором машинном коде. Последний быстро обрабатывается и позволяет расширить объемы декодируемых данных. Однако для этого следует знать определенную методику и немного предыстории развития вычислительной техники.
Общие сведения
Во время изобретения персонального компьютера (ПК) или ЭВМ использовался определенный язык представления данных, который существенно отличался от десятичной системы счисления. Последняя используется человеком при ведении расчетов и является самой удобной.
Кодирование данных в современных ЭВМ осуществляется за счет элементов (транзисторов) в интегральных микросхемах. За основу взят полупроводниковый переход, который может быть закрытым или открытым. Следует отметить, что режим «насыщения», присущий радиодетали, не используется. Если он открыт, то в триггер (память) записывается единица, а в противном случае — нуль. В результате этого кодирование осуществляется в двоичном коде (0 или 1), основанием которого является цифра «2».
Для кодирования больших массивов информации использовать двоичную систему счисления не всегда удобно, поскольку количество транзисторов может быть огромным, а устройство будет значительно греться. Чтобы этого избежать, была придумана восьмеричная система счисления.
Для выполнения операции конвертации десятичной системы исчисления в восьмеричный код необходимы некоторые базовые знания. К ним относятся:
Специалисты в области информационных технологий рекомендуют разбирать базовые понятия в последовательности, состоящей из пяти шагов.
Число и цифра
При расчетах и выражении количественных характеристик процесса или явления применяются определенные математические символы — числа. Они состоят из разрядной сетки. Каждый ее элемент — цифра, которая принимает значения, в зависимости от выбранной системы счисления (СС). Например, для десятичной используется диапазон от 0 до 9, а девятеричная состоит из интервала с минимальной величиной, равной 0, а максимальной — 8.
Цифра — математический знак, используемый для построения более сложных конструкций. Например, с его помощью можно записать значения различных типов (четырехзначные, пятизначные). Любое число состоит из разрядной сетки, элементами которой и являются математические символы.
При выполнении различных математических операций нужно следить за одинаковыми разрядами. Например, недопустимо складывать сотни и тысячи, поскольку это действие приведет к ошибочным вычислениям. Далее следует разобрать системы представления информации и их примеры.
Виды числовых представлений
Для правильного перевода чисел из одной СС в другую необходимо разобрать классификацию форм представления информации. Они бывают двух типов, в зависимости от расположения цифр:
В первом случае значение числа зависит от расположения или комбинации цифр. Этот факт очень просто доказывается на примере обычной десятичной формы представления величины. Например, 25 и 52 — два разных значения. Если бы расположение разрядов не учитывалось, при разности этих двух величин получился нуль. Позиционными СС являются двоичный, восьмеричный и шестнадцатеричный коды. В них также есть разрядная сетка.
Независимыми от расположения разрядов называются непозиционные СС. Примером одной из них является унарная форма записи числа. Суть ее заключается в эквивалентности символа какому-либо значению. Например, на предприятиях применяются обыкновенные «крестики» для подсчета количества рабочих дней сотрудников. Каждый символ эквивалентен единице.
На уроках математики в начальных классах также применяется инструмент — счетные палочки. Последние помогают ученикам развивать навык устного счета и являются компонентами непозиционной СС. С их помощью возможно выполнять операции суммы, разности, а также произведения и деления.
Следует отметить, что не во всех случаях один символ может соответствовать единице. Это могут быть десятки, сотни и даже тысячи. Для расчетов при помощи непозиционной СС можно придумать собственные обозначения, как это сделано в римских цифрах. Однако при этом существуют определенные недостатки:
Достоинством считается сокращение времени записи величины, которая постоянно изменяется. Например, при подсчете количества выходов персонала достаточно поставить крестик или палочку, и это делается без исправлений. В случае с десятичной СС исправлений избежать невозможно.
Чтобы выполнить перевод в восьмеричную систему счисления, необходимо ознакомиться с методикой конвертации десятичной формы в двоичное кодовое представление.
Двоичная кодировка
Для преобразования десятичной величины в двоичную IT-специалистами были разработаны специальные правила или алгоритмы. К ним относятся столбик и степень. Каждому начинающему IT-специалисту необходимо выбрать оптимальную методику преобразования одной формы числа в другую. Каждый из способов удобен в конкретной ситуации. Можно также применять сразу 2 — один для решения, а другой — для проверки результата. Необходимо разобрать каждую методику подробно с практической реализацией алгоритма.
Метод «столбик»
Первый способ получил широкое применение, поскольку для его выполнения требуется минимум знаний в математической сфере. Он имеет следующий вид:
Реализация алгоритма проверяется на практическом примере. Для этого требуется решить задачу конвертации числа из десятичной СС в другую, перевод 167 <10>в <2>. Решение имеет следующий вид:
Обратный алгоритм конвертации из двоичной в десятичную форму представления величины основан на соответствии значений степенным показателям двойки. Разбиение на разрядную сетку осуществляется справа налево. Методика имеет такой вид:
Реализация методики проверяется на практическом примере — следует взять двоичный код из предыдущего задания, т. е. 10100111. Алгоритм нахождения десятичной формы имеет следующий вид:
Переводить системы счисления в другие формы представления возможно при помощи различных онлайн-сервисов. Для этого требуется указать исходную форму числа, а затем конечную. Однако действия рекомендуется совершать только для проверки результата решения задачи.
Способ степени
Для конвертации в двоичный код также применяется метод степени. Суть его заключается в представлении числа в виде отдельных элементов с основанием «2» и некоторым показателем. Алгоритм в этом случае выглядит таким образом:
Как и во всех остальных случаях, рекомендуется разобрать алгоритм на практическом примере. Решение задачи для числа «167» имеет такой вид:
Однако операция преобразования является вспомогательной. Она применяется для дальнейшей конвертации в восьмеричную СС.
Восьмеричная система
Восьмеричная форма представления чисел состоит из основания-восьмерки и триады. Совокупность последних образуют любые значения. Для кодирования информации в этом случае применяется меньше регистров памяти. Этого нельзя сказать о двоичном коде.
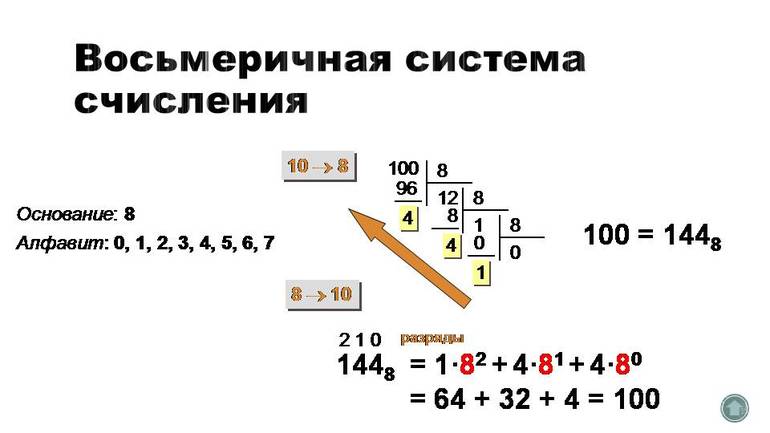
Для восьмеричного представления применяются цифры от 0 до 7 (всего 8). Многие новички часто путают ее с шестнадцатеричной СС, в которой содержатся символы латинского алфавита. При выполнении операций конвертации специалисты рекомендуют ознакомиться со списком (таблицей) восьмеричной системы:
Он поможет перевести любое числовое сообщение. Для удобства IT-специалисты рекомендуют составить презентацию или записать на лист плотной бумаги перекодировку списка. Заучивать коды нет необходимости, поскольку достаточно решать примеры (информация отложится в памяти). Алгоритм кодирования очень прост:
После ознакомления с методикой преобразования нужно проверить ее реализацию на примере. Требуется выяснить, значение 167 <10>. Это делается довольно просто:
Обратное декодирование выполняется по такой методике:
На начальных этапах обучения рекомендуется четко следовать по пунктам методики. Однако через некоторое время последние можно опускать.
Таким образом, восьмеричная система применяется для кодирования больших массивов информации, при котором может быть задействовано минимальное количество регистров запоминающего устройства персонального компьютера.