Для чего нужно измерение информации
Свойства информации
Плохое определение информации (на мой взгляд)
Зачем нужно измерять информацию
Вопрос о количестве и, следовательно, мере измерения информации возник тогда, когда:
· Когда информатика стала оформляться в науку, то есть в систему знаний, включающих в себя различные отношения между понятиями и величинами, как логическими, так и количественными;
· Когда инженерам понадобились точные количественные характеристики устройств, обеспечивающих переработку информации.
Но чтобы ввести меру информации надо ещё раз определить, а что, же это такое – информация, в чём её суть. Определение информации как следа от взаимодействия объектов на этих объектах не очень способствует введению меры для оценки её количества.
2. Рассуждения о сущности информации и её свойствах
Моё определение информации. Информация– сформированная (выработанная) человеческим обществом понятийная сущность, позволяющая описывать и оперировать другими понятийными сущностями, а также меру определённости знания об окружающих живой объект действительности, отображая её в количественной, логической или языковой формах.
Понятийная сущность – существующая в материальных структурах мозга связь между зафиксированными в словах (и других фигурах речи и логики) другими понятиями – то есть определяемая через них.
Вопрос – носит ли понятийная сущность материальный или нематериальный характер?
Мой ответ – любая высказанная мысль[1] (в устной или письменной форме) отрывается от субъекта её породившего. Далее она распространяется независимо от него. Но может воздействовать на другой субъекта только в том случае, если
· у последнего существуют созданные заранее структуры, обрабатывающие мысль или любой примитивный сигнал;
· между двумя объектами существует среда передачи.
Поэтому, на мой взгляд, любая понятийная сущность в своей основе носит материальный характер, хотя это не всегда осознаётся носителем структуры по обработке этих сущностей – человеческим мозгом.
Однако, в зависимости от области деятельности человека, возможны варианты различные типы информационных сущностей. Поэтому понятие «информация» имеет различные трактовки в разных предметных областях.
Например, информация может пониматься как:
· абстракция, абстрактная модель рассматриваемой системы (в математике);
· сигналы для управления, приспособления рассматриваемой системы (в кибернетике);
· мера хаоса в рассматриваемой системе (в термодинамике);
· вероятность выбора в рассматриваемой системе (в теории вероятностей);
· мера разнообразия в рассматриваемой системе (в биологии) и др.
Однако в человеческом обществе материальная сущность информации может быть очень сильно замаскирована. Пример: текст песни или рассказа, юридические законы, математические формулы и.т.д..
Эти примеры показывают, что взаимодействие в человеческом обществе может быть:
1. Опосредованным, то есть передача может происходить через искусственно созданные объекты;
2. Отложенным – то есть происходить через неопределённое время;
3. Носить социальный и нравственный характер – то есть быть обращённой к обществу, а не к конкретной личности, а также востребоваться самим преемником по мере необходимости ( по желанию приёмника)
Рассмотрим понятие информации на основе понятия «алфавит» («алфавитный», формальный подход). Дадим формальное определение алфавита.
Алфавит – конечное множество различных знаков, символов, для которых определена операция конкатенации (приписывания, присоединения символа к символу или цепочке символов); с ее помощью по определенным правилам соединения символов и слов можно получать слова (цепочки знаков) и словосочетания (цепочки слов) в этом алфавите (над этим алфавитом).
Буквой или знаком называется любой элемент x алфавита X, где 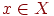
Примеры алфавитов: множество из десяти цифр, множество из знаков русского языка, точка и тире в азбуке Морзе и др. В алфавите цифр знак 5 связан с понятием «быть в количестве пяти элементов».
Конечная последовательность букв алфавита называется словом в алфавите (или над алфавитом).
Длиной p некоторого слова p над алфавитом Х называется число составляющих его букв.
Слово (обозначаемое символом Ø) имеющее нулевую длину, называется пустым словом: |Ø| = 0.
Множество различных слов над алфавитом X обозначим через S(X) и назовем словарным запасом (словарем) алфавита (над алфавитом) X.
В отличие от конечного алфавита, словарный запас может быть и бесконечным.
Слова над некоторым заданным алфавитом и определяют так называемые сообщения.
Таким образом, алфавит должен позволять решать задачу лексикографического (алфавитного) упорядочивания, или задачу расположения слов над этим алфавитом, в соответствии с порядком, определенным в алфавите (то есть по символам алфавита).
Информация содержится не в одном слове, а в предложении или совокупности предложений.
Информация – это некоторая упорядоченная последовательность сообщений, отражающих, передающих и увеличивающих наши знания
Информация актуализируется с помощью различной формы сообщений – определенного вида сигналов, символов.
Информация по отношению к источнику или приемнику бывает трех типов: входная, выходная и внутренняя.
Информация по отношению к конечному результату бывает исходная, промежуточная и результирующая.
Информация по ее изменчивости бывает постоянная, переменная и смешанная.
Информация по стадии ее использования бывает первичная и вторичная.
Информация по ее полноте бывает избыточная, достаточная и недостаточная.
Информация по доступу к ней бывает открытая и закрытая.
Есть и другие типы классификации информации.
В философском аспекте информация делится на мировоззренческую, эстетическую, религиозную, научную, бытовую, техническую, экономическую, технологическую.
Основные свойства информации (Шум, очевидно, не обладает этими свойствами):
Высшей формой информации являются знания.
Из вышеприведенного возникает сомнение, а возможна ли единая мера для оценки количества информации, или хотя бы понимания того, когда и о чём её больше, а когда меньше.
Действительно, существуют разные подходы к оценке количества информации, учитывающие её качественную сторону:
а. Аксиологический подход – учитывает ценность информации:
б.Семантический подход – учитывает форму, содержание в связи с необходимостью владения тезаурусом (словарём) источника и приёмника информации
С практической точки зрения нужно рассмотреть два подхода: вероятностный и полный.
Любые сообщения измеряются в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах, петабайтах и эксабайтах, а кодируются, например, в компьютере, с помощью алфавита из нулей и единиц, записываются и реализуются в ЭВМ в битах.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Для чего нужно измерение информации
Измерение информации: содержательный и алфавитный подходы. Единицы измерения информации.
Вопрос: «Как измерить информацию?» очень непростой. Ответ на него зависит от того, что понимать под информацией. Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными.
Содержательный подход к измерению информации.
Для человека информация — это знания человека. Рассмотрим вопрос с этой точки зрения.
Получение новой информации приводит к расширению знаний. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию.
Отсюда следует вывод, что сообщение информативно (т.е. содержит ненулевую информацию), если оно пополняет знания человека. Например, прогноз погоды на завтра — информативное сообщение, а сообщение о вчерашней погоде неинформативно, т.к. нам это уже известно.
Нетрудно понять, что информативность одного и того же сообщения может быть разной для разных людей. Например: «2×2=4» информативно для первоклассника, изучающего таблицу умножения, и неинформативно для старшеклассника.
Но для того чтобы сообщение было информативно оно должно еще быть понятно. Быть понятным, значит быть логически связанным с предыдущими знаниями человека. Определение «значение определенного интеграла равно разности значений первообразной подынтегральной функции на верхнем и на нижнем пределах», скорее всего, не пополнит знания и старшеклассника, т.к. оно ему не понятно. Для того, чтобы понять данное определение, нужно закончить изучение элементарной математики и знать начала высшей.
Получение всяких знаний должно идти от простого к сложному. И тогда каждое новое сообщение будет в то же время понятным, а значит, будет нести информацию для человека.
Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными.
Алфавитный подход к измерению информации.
Один символ алфавита «весит» 8 бит. Причем 8 бит информации — это настолько характерная величина, что ей даже присвоили свое название — байт.
Сегодня очень многие люди для подготовки писем, документов, статей, книг и пр. используют компьютерные текстовые редакторы. Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов.
В любой системе единиц измерения существуют основные единицы и производные от них.
Для измерения больших объемов информации используются следующие производные от байта единицы:
Презентация к уроку
Цель урока: формирование знаний, умений и навыков расчета единиц измерения информации, определения информационного объема сообщений, возможность практического применения полученных знаний.
Планируемые результаты обучения:
Понятие об информации
С точки зрения физики, наш мир состоит из трех элементов: вещество, энергия, информация.
«Информация» является центральным понятием информатики. Точного определения этого понятия в науке не существует. На бытовом уровне, информация это сообщения, знания, которые человек получает из окружающего мира: общаясь с другими людьми, из книг, Интернета, СМИ и т.д. Понятие отличается от определения тем, что не дается однозначно, а вводится на примерах. При чем каждая наука это делает по своему.
Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными.
Содержательный подход к измерению информации
Информация – это знания человека. Сообщение несет информацию для человека (информативно), если содержащиеся в нем сведения являются для него новыми и понятными.
Сообщение, уменьшающее неопределенность знаний в два раза, несет 1 бит информации.
Неопределенность знаний о некотором событии – это количество возможных результатов события. Что такое “неопределенность знаний”? Рассмотрим пример: Вы бросаете монету, загадывая, что выпадет: орел или решка? Есть два варианта возможного результата бросания монеты. Ни один из этих вариантов не имеет преимущества перед другим (равновероятны). Перед подбрасыванием монеты неопределенность знаний о результате равна двум. После совершения действия неопределенность уменьшилась в 2 раза. Получили 1 бит информации. Результат подбрасывания монеты принес 1 бит информации.
Еще пример: после сдачи зачета или выполнения контрольной работы ученик мучается неопределенностью, он не знает, какую оценку получил. Наконец, учитель объявляет результаты, и он получаете одно из двух информационных сообщений: “зачет” или “незачет”, а после контрольной работы одно из четырех информационных сообщений: “2”, “3”, “4” или “5”.
Информационное сообщение об оценке за зачет приводит к уменьшению неопределенности знания в два раза, так как получено одно из двух возможных информационных сообщений. Информационное сообщение об оценке за контрольную работу приводит к уменьшению неопределенности знания в четыре раза, так как получено одно из четырех возможных информационных сообщений.
Неопределенность знаний о некотором событии — это количество возможных результатов события.
Если обозначить возможное количество событий, или, другими словами, неопределенность знаний N, а буквой i количество информации в сообщении о том, что произошло одно из N событий, то можно записать формулу:
которую используют для решения задач на содержательный подход к измерению информации.
В презентации рассматриваются примеры решения задач по этой теме, а также предлагается решить задачи самостоятельно и проверить ответы (Презентация: слайды 10, 11, 12, 13).
Единицы измерения информации
Бит – наименьшая единица представления информации.
Байт – наименьшая единица обработки и передачи информации.
Один байт равен восьми битам, т.к. именно восемь битов требуется для того, чтобы закодировать любой из 256 символов алфавита клавиатуры компьютера (256=2 8 ).
Для перевода из крупных единиц в мелкие числа умножают, согласно таблице переводов
Пример:
2 Кбайта = 2 * (1 Кбайт) = 2 * 1024 байтов = 2048 байтов = 2048 * 8 бит = 16384 бита.
или можно считать так, так иногда проще:
2 Кбайта = 2 * 2 10 байтов = 2 11 байт = 2 11 * 2 3 бит = 2 14 бит
Для перевода количества информации из мелких единиц в более крупные нужно делить.
Пример:
8192 бита = 8192 : 8 (т.к. в 1 байте 8 бит) = 1024 байт = 1024 : 1024 (т.к. в 1 Кбайте 1024 байт) = 1 Кбайт
или можно считать так
8192 бита = 2 13 бит = 2 13 : 2 3 = 2 10 байт = 2 10 : 2 10 = 1 Кбайт
Примеры объемов информации
Страница книги 2,5 Кбайт Учебник 0,5 Мбайт Газета 150 Кбайт Черно-белый кадр 300 Кбайт Цветной кадр из 3 цветов 1 Мбайт 1,5 часовой цветной фильм 135 Гбайт
В презентации рассматриваются примеры решения задач по этой теме, а также предлагается решить задачи самостоятельно и проверить ответы (Презентация: слайды 19, 20, 21).
Алфавитный подход к измерению информации
Алфавитный подход к измерению количества информации основан на подсчете числа символов в сообщении. При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы. Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами. Полное количество символов алфавита принято называть мощностью алфавита.
N = 2 i – формула для решения задач на алфавитный подход к измерению информации.
N – мощность алфавита
i – количество информации одного символа
В презентации рассматриваются примеры решения задач по этой теме, а также предлагается решить задачи самостоятельно и проверить ответы (Презентация: слайды 26, 27, 28, 29, 30)
Решения заданий практикума представлены в Приложении 2
Домашнее задание находится в презентации на слайдах 14, 22, 30.
Интерактивный тест можно пройти на слайде 32.
Измерение информации

Всего получено оценок: 415.
Всего получено оценок: 415.
Как и любую другую физическую величину, информацию можно измерить. Существуют разные подходы к измерению информации. Один из таких подходов рассматривается в курсе информатики за 7 класс.
Что такое измерение информации
При измерении информации следует учитывать как объем передаваемого сообщения, так и его смысловую нагрузку. В связи с этим в информатике существуют разные подходы к измерению информации.
Алфавитный подход к измерению информации
Способы оценки величины информации могут учитывать или не учитывать смысла информационного сообщения.
Один из способов нахождения количества информации основан на определении веса каждого символа в тексте сообщения. При таком подходе объем сообщения зависит от количества знаков в тексте, чем больше тест, тем больше весит информационное сообщение. При этом абсолютно не важно, что написано, какой смысл несет сообщение. Так как определение объема информации привязано к текстовым единицам: буквам, цифрам, знакам препинания, то такой подход к измерению информации получил название алфавитного.
Вес отдельного знака зависит от их количества в алфавите. Число символов алфавита называют мощностью (N). Например, мощность алфавита английского языка по числу символов равно 26, русского языка 33. Но на самом деле, при написании текста используются и прописные и строчные буквы, а также знаки препинания, пробелы и специальные невидимые символы, обозначающие конец абзаца и перевод к новой строке. Поэтому имеют дело с мощностью 128 или в расширенной версии 256 символов.
Бит, байт и другие единицы измерения
Для двоичного алфавита, состоящего из двух символов – нуля и единицы, мощность алфавита будет составлять 2. Вес символа бинарного алфавита выбран в качестве минимальной единицы информации и называется «бит». Происхождение термина «бит» исходит от англоязычного слова «binary», что означает двоичный.
Восемь бит образуют байт.
Название «байт» было придумано в 1956 году В. Бухгольцем при проектировании первого суперкомпьютера. Слово «byte» было получено путем замены второй буквы в созвучном слове «bite», чтобы избежать путаницы с уже имеющимся термином «bit».
На практике величина объема информации выражает в более крупных единицах: килобайтах, терабайтах, мегабайтах.
Следует запомнить, что килобайт равен 1024 байта, а не 1000. Как, например, 1 километр равен 1000 метрам. Эта разница получается за счет того, 1 байт равен 8 битам, а не 10.
Для того, чтобы легче запомнить единицы измерения, следует воспользоваться таблицей степени двойки.
Таблица степеней двойки
Показатель степени
Значение
То есть, 2 3 = 8 – это 1 байт, состоящий из 8 бит, 2 10 = 1024 это 1 килобайт, 2 20 = 1048576 представляет собой 1 мегабайт, 2 30 = 1 гигабайт, 2 40 = 1 терабайт.
Определение количества информации
Вес символа (i) и мощность алфавита (N) связаны между собой соотношением: 2 i = N.
Так, алфавит мощностью в 256 символов имеет вес каждого символа в 8 бит, то есть один байт. Это означает, что на каждую букву приходится по байту. В таком случае, нетрудно определить, сколько весит весь кодируемый текст сообщения. Для этого достаточно вес символа алфавита умножить на количество символов в тексте. При подсчете количества символов в сообщении следует не забывать, что знаки препинания, а также пробелы – это тоже символы и они весят столько же, сколько и буквы.
Например, при условии, что каждая буква кодируется одним байтом, для текста, «Ура! Наступили каникулы.» информационный объем определяется умножением 8 битов на 24 символа (без учета кавычек). Произведение 8 * 24 = 192 бита – столько весит кодируемая фраза. В переводе на байты: 192 бита разделить на 8 получим 24 байта.
Эта схема работает и в обратной задаче. Пусть информационное сообщение составляет 2 килобайта и состоит из 512 символов. Необходимо определить мощность алфавита, используемого для кодирования сообщения.
Решение: Сначала целесообразно 2 килобайта перевести в биты: 2 * 1024 = 2048 (бит). Затем объем информационного сообщения делят на количество символов: 2048 / 512 = 4 (бит), получают вес одного символа. Для определения мощности алфавита 2 возводят в степень 4 и получают 16 – это мощность алфавита, то есть количество символов, используемых для кодирования текста.
Что мы узнали?
Одним из способов определения величины информационного сообщения является алфавитный подход, в котором любой знак в тексте имеет некоторый вес, обусловленный мощностью алфавита. Минимальной единицей измерения информации является бит. Информацию можно также измерять в байтах, килобайтах, мегабайтах.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 1.6. Измерение информации
Информатика. 7 класса. Босова Л.Л. Оглавление
1.6.1. Алфавитный подход к измерению информации
Одно и то же сообщение может нести много информации для одного человека и не нести её совсем для другого человека. При таком подходе количество информации определить однозначно затруднительно.
Алфавитный подход позволяет измерить информационный объём сообщения, представленного на некотором языке (естественном или формальном), независимо от его содержания.
Для количественного выражения любой величины необходима, прежде всего, единица измерения. Измерение осуществляется путём сопоставления измеряемой величины с единицей измерения. Сколько раз единица измерения «укладывается» в измеряемой величине, таков и результат измерения.
При алфавитном подходе считается, что каждый символ некоторого сообщения имеет определённый информационный вес — несёт фиксированное количество информации. Все символы одного алфавита имеют один и тот же вес, зависящий от мощности алфавита. Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется 1 бит.
Обратите внимание, что название единицы измерения информации «бит» (bit) происходит от английского словосочетания binary digit — «двоичная цифра».
За минимальную единицу измерения информации принят 1 бит. Считается, что таков информационный вес символа двоичного алфавита.
1.6.2. Информационный вес символа произвольного алфавита
Разрядность двоичного кода принято считать информационным весом символа алфавита. Информационный вес символа алфавита выражается в битах.
Задача 1. Алфавит племени Пульти содержит 8 символов. Каков информационный вес символа этого алфавита?
Решение. Составим краткую запись условия задачи.
Полная запись решения в тетради может выглядеть так:
1.6.3. Информационный объём сообщения
Информационный объём сообщения (количество информации в сообщении), представленного символами естественного или формального языка, складывается из информационных весов составляющих его символов.
Информационный объём сообщения I равен произведению количества символов в сообщении К на информационный вес символа алфавита i;I = К • i.
Задача 2. Сообщение, записанное буквами 32-символьного алфавита, содержит 140 символов. Какое количество информации оно несёт?
Задача 3. Информационное сообщение объёмом 720 битов состоит из 180 символов. Какова мощность алфавита, с помощью которого записано это сообщение?
1.6.4. Единицы измерения информации
1 байт = 8 битов
Бит и байт — «мелкие» единицы измерения. На практике для измерения информационных объёмов используются более крупные единицы:
1 килобайт = 1 Кб = 1024 байта = 2 10 байтов
1 мегабайт = 1 Мб = 1024 Кб = 2 10 Кб = 2 20 байтов
1 гигабайт = 1 Гб = 1024 Мб = 2 10 Мб = 2 20 Кб = 2 30 байтов
1 терабайт = 1 Тб = 1024 Гб = 2 10 Гб = 2 20 Мб = 2 30 Кб = 2 40 байтов
Задача 4. Информационное сообщение объёмом 4 Кбайта состоит из 4096 символов. Каков информационный вес символа используемого алфавита? Сколько символов содержит алфавит, с помощью которого записано это сообщение?
Ответ: 8 битов, 256 символов.
Задача 5. В велокроссе участвуют 128 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер цепочкой из нулей и единиц минимальной длины, одинаковой для каждого спортсмена. Каков будет информационный объём сообщения, записанного устройством после того, как промежуточный финиш пройдут 80 велосипедистов?
Ответ: 70 байтов.
Самое главное.
При алфавитном подходе считается, что каждый символ некоторого сообщения имеет опредёленный информационный вес — несёт фиксированное количество информации.
1 бит — минимальная единица измерения информации.
Информационный объём сообщения I равен произведению количества символов в сообщении К на информационный вес символа алфавита i: I = K•i.
Байт, килобайт, мегабайт, гигабайт, терабайт — единицы измерения информации. Каждая следующая единица больше предыдущей в 1024 (210) раза.
Вопросы и задания.
1.Ознакомтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.






