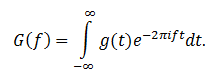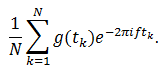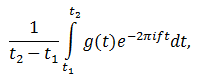Для чего нужно преобразование фурье
Понимание алгоритма БПФ
Здравствуйте, друзья. Уже завтра стартует курс «Алгоритмы для разработчиков», а у нас остался один неопубликованный перевод. Собственно исправляемся и делимся с вами материалом. Поехали.
Быстрое преобразование Фурье (БПФ — англ. FFT) является одним из важнейших алгоритмов обработки сигналов и анализа данных. Я пользовался им годами, не имея формальных знаний в области компьютерных наук. Но на этой неделе мне пришло в голову, что я никогда не задавался вопросом, как БПФ так быстро вычисляет дискретное преобразование Фурье. Я стряхнул пыль со старой книги по алгоритмам, открыл ее, и с удовольствием прочитал об обманчиво простой вычислительной уловке, которую Дж. В. Кули и Джон Тьюки описали в своей классической работе 1965 года, посвященной этой теме.
Цель этого поста — окунуться в алгоритм БПФ Кули-Тьюки, объясняя симметрии, которые к нему приводят, и показать несколько простых реализаций на Python, применяющих теорию на практике. Я надеюсь, что это исследование даст специалистам по анализу данных, таким как я, более полную картину того, что происходит под капотом используемых нами алгоритмов.
Дискретное преобразование Фурье
БПФ — это быстрый алгоритм для вычисления дискретного преобразования Фурье (ДПФ), которое напрямую вычисляется за . ДПФ, как и более знакомая непрерывная версия преобразования Фурье, имеет прямую и обратную форму, которые определяются следующим образом:
Прямое дискретное преобразование Фурье (ДПФ):
Обратное дискретное преобразование Фурье (ОДПФ):
Преобразование из xn → Xk является переводом из конфигурационного пространства в пространство частотное и может быть очень полезным как для исследования спектра мощности сигнала, так и для преобразования определенных задач для более эффективного вычисления. Некоторые примеры этого в действии вы можете найти в главе 10 нашей будущей книги по астрономии и статистике, где также можно найти изображения и исходный код на Python. Пример использования БПФ для упрощения интегрирования сложных в противном случае дифференциальных уравнений смотрите в моем посте «Решение уравнения Шредингера в Python».
Из-за важности БПФ (далее может быть использовано равносильное FFT — Fast Fourier Transform) во многих областях Python содержит множество стандартных инструментов и оболочек для его вычисления. И NumPy, и SciPy имеют оболочки из чрезвычайно хорошо протестированной библиотеки FFTPACK, которые находятся в подмодулях numpy.fft и scipy.fftpack соответственно. Самый быстрый БПФ, о котором я знаю, находится в пакете FFTW, который также доступен в Python через пакет PyFFTW.
На данный момент, однако, давайте оставим эти реализации в стороне и зададимся вопросом, как мы можем вычислить БПФ в Python с нуля.
Вычисление дискретного преобразования Фурье
Для простоты мы будем касаться только прямого преобразования, поскольку обратное преобразование может быть реализовано очень похожим образом. Взглянув на приведенное выше выражение ДПФ (DFT), мы видим, что это не более чем прямолинейная линейная операция: умножение матрицы на вектор
с матрицей М, заданной
Имея это в виду, мы можем вычислить ДПФ с использованием простого умножения матрицы следующим образом:
Мы можем перепроверить результат, сравнив его со встроенной в numpy БПФ-функцией:
Просто чтобы подтвердить медлительность нашего алгоритма, мы можем сравнить время выполнения этих двух подходов:
Мы более чем в 1000 раз медленнее, что и следовало ожидать для такой упрощенной реализации. Но это не самое худшее. Для входного вектора длины N алгоритм БПФ масштабируется как , в то время как наш медленный алгоритм масштабируется как . Это означает, что для элементов мы ожидаем, что БПФ завершится за где-то около 50 мс, в то время как наш медленный алгоритм займет около 20 часов!
Так как же БПФ добивается такого ускорения? Ответ заключается в использовании симметрии.
Симметрии в дискретном преобразовании Фурье
Одним из наиболее важных инструментов в построении алгоритмов является использование симметрий задачи. Если вы можете аналитически показать, что одна часть проблемы просто связана с другой, вы можете вычислить подрезультат только один раз и сэкономить эти вычислительные затраты. Кули и Тьюки использовали именно этот подход при получении БПФ.
Мы начнем с вопроса о значении . Из нашего выражения выше:
где мы использовали тождество exp [2π i n] = 1, которое выполняется для любого целого числа n.
Последняя строка хорошо показывает свойство симметрии ДПФ:
для любого целого числа i. Как мы увидим ниже, эту симметрию можно использовать для гораздо более быстрого вычисления ДПФ.
ДПФ в БПФ: использование симметрии
Кули и Тьюки показали, что можно разделить вычисления БПФ на две меньшие части. Из определения ДПФ имеем:
Мы разделили одно дискретное преобразование Фурье на два слагаемых, которые сами по себе очень похожи на меньшие дискретные преобразования Фурье, одно на значения с нечетным номером и одно на значения с четным номером. Однако до сих пор мы не сохранили никаких вычислительных циклов. Каждый член состоит из (N / 2) ∗ N вычислений, всего .
Хитрость заключается в использовании симметрии в каждом из этих условий. Поскольку диапазон k равен 0≤k True
Сопоставим этот алгоритм с нашей медленной версией:
-In [6]:
Наш расчет быстрее чем прямая версия на порядок! Более того, наш рекурсивный алгоритм асимптотически : мы реализовали быстрое преобразование Фурье.
Обратите внимание, что мы все еще не приблизились к скорости встроенного алгоритма FFT в numpy, и этого следовало ожидать. Алгоритм FFTPACK, стоящий за fft numpy, — это реализация на Фортране, которая получила годы доработок и оптимизаций. Кроме того, наше решение NumPy включает в себя как рекурсию стека Python, так и выделение множества временных массивов, что увеличивает время вычислений.
Хорошая стратегия для ускорения кода при работе с Python / NumPy — по возможности векторизовать повторяющиеся вычисления. Это мы можем сделать — в процессе удалять наши рекурсивные вызовы функций, что сделает наш Python FFT еще более эффективным.
Обратите внимание, что в вышеупомянутой рекурсивной реализации FFT на самом низком уровне рекурсии мы выполняем N / 32 идентичных матрично-векторных произведений. Эффективность нашего алгоритма выиграет, если одновременно вычислить эти матрично-векторные произведения как единое матрично-матричное произведение. На каждом последующем уровне рекурсии мы также выполняем повторяющиеся операции, которые можно векторизовать. NumPy отлично справляется с такой операцией, и мы можем использовать этот факт для создания этой векторизованной версии быстрого преобразования Фурье:
Хотя алгоритм немного более непрозрачен, это просто перестановка операций, используемых в рекурсивной версии, с одним исключением: мы используем симметрию в вычислении коэффициентов и строим только половину массива. Опять же, мы подтверждаем, что наша функция дает правильный результат:
Поскольку наши алгоритмы становятся намного более эффективными, мы можем использовать больший массив для сравнения времени, оставляя DFT_slow :
In [9]:
Мы улучшили нашу реализацию еще на порядок! Сейчас мы находимся на расстоянии примерно в 10 раз от эталона FFTPACK, используя всего пару десятков строк чистого Python + NumPy. Хотя это все еще не соответствует в вычислительном отношении, с точки зрения читаемости версия Python намного превосходит исходный код FFTPACK, который вы можете просмотреть здесь.
Итак, как FFTPACK достигает этого последнего ускорения? Ну, в основном, это просто вопрос детальной бухгалтерии. FFTPACK тратит много времени на повторное использование любых промежуточных вычислений, которые можно использовать повторно. Наша клочковатая версия все еще включает в себя избыток выделения памяти и копирования; на низкоуровневом языке, таком как Fortran, легче контролировать и минимизировать использование памяти. Кроме того, алгоритм Кули-Тьюки можно расширить, чтобы использовать разбиения размером, отличным от 2 (то, что мы здесь реализовали, известно как БПФ Кули-Тьюки радикса по основе 2). Также могут быть использованы другие более сложные алгоритмы БПФ, в том числе принципиально отличные подходы, основанные на сверточных данных (см., Например, алгоритм Блюштейна и алгоритм Рейдера). Комбинация вышеупомянутых расширений и методов может привести к очень быстрым БПФ даже на массивах, размер которых не является степенью двойки.
Хотя функции на чистом Python, вероятно, бесполезны на практике, я надеюсь, что они преподнесли некоторую интуицию в том, что происходит на фоне анализа данных на основе FFT. Как специалисты по данным, мы можем справиться с реализацией «черного ящика» фундаментальных инструментов, созданных нашими более алгоритмически настроенными коллегами, но я твердо убежден, что чем больше у нас понимания о алгоритмах низкого уровня, которые мы применяем к нашим данным, тем лучшими практиками мы будем.
Этот пост был полностью написан в блокноте IPython. Полный блокнот можно скачать здесь или посмотреть статически здесь.
Многие могут заметить, что материал далеко не новый, но, как нам кажется, вполне актуальный. В общем пишите была ли статья полезной. Ждём ваши комментарии.
Простыми словами о преобразовании Фурье
Я полагаю что все в общих чертах знают о существовании такого замечательного математического инструмента как преобразование Фурье. Однако в ВУЗах его почему-то преподают настолько плохо, что понимают как это преобразование работает и как им правильно следует пользоваться сравнительно немного людей. Между тем математика данного преобразования на удивление красива, проста и изящна. Я предлагаю всем желающим узнать немного больше о преобразовании Фурье и близкой ему теме того как аналоговые сигналы удается эффективно превращать для вычислительной обработки в цифровые.
(с) xkcd
Я буду исходить из предположения что читатель понимает что такое интеграл, комплексное число (а так же его модуль и аргумент), свертка функций, плюс хотя бы “на пальцах” представляет себе что такое дельта-функция Дирака. Не знаете — не беда, прочитайте вышеприведенные ссылки. Под “произведением функций” в данном тексте я везде буду понимать “поточечное умножение”
Начать надо, наверное, с того что обычное преобразование Фурье — это некая такая штука которая, как можно догадаться из названия, преобразует одни функции в другие, то есть ставит в соответствие каждой функции действительного переменного x(t) её спектр или фурье-образ y(w):
Если приводить аналогии, то примером аналогичного по смыслу преобразования может послужить например дифференцирование, превращающее функцию в её производную. То есть преобразование Фурье — такая же, по сути, операция как и взятие производной, и её часто обозначают схожим образом, рисуя треугольную “шапочку” над функцией. Только в отличие от дифференцирования которое можно определить и для действительных чисел, преобразование Фурье всегда “работает” с более общими комплексными числами. Из-за этого постоянно возникают проблемы с отображением результатов этого преобразования, поскольку комплексные числа определяются не одной, а двумя координатами на оперирующем действительными числами графике. Удобнее всего, как правило, оказывается представить комплексные числа в виде модуля и аргумента и нарисовать их по раздельности как два отдельных графика:
График аргумента комплексного значения часто называют в данном случае “фазовым спектром”, а график модуля — “амплитудным спектром”. Амплитудный спектр как правило представляет намного больший интерес, а потому “фазовую” часть спектра нередко пропускают. В этой статье мы тоже сосредоточимся на “амплитудных” вещах, но забывать про существование пропущенной фазовой части графика не следует. Кроме того, вместо обычного модуля комплексного значения часто рисуют его десятичный логарифм умноженный на 10. В результате получается логарифмический график, значения на котором отображаются в децибелах (дБ).
Обратите внимание что не очень сильно отрицательным числам логарифмического графика (-20 дБ и менее) при этом соответствуют практически нулевые числа на графике “обычном”. Поэтому длинные и широкие “хвосты” разнообразных спектров на таких графиках при отображении в “обычные” координаты как правило практически исчезают. Удобство подобного странного на первый взгляд представления возникает из того что фурье-образы различных функций часто необходимо перемножать между собой. При подобном поточечном умножении комплекснозначных фурье-образов их фазовые спектры складываются, а амплитудные — перемножаются. Первое выполняется легко, а второе — сравнительно сложно. Однако логарифмы амплитуды при перемножении амплитуд складываются, поэтому логарифмические графики амплитуды можно, как и графики фаз, просто поточечно складывать. Кроме того, в практических задачах часто удобнее оперировать не «амплитудой» сигнала, а его «мощностью» (квадратом амплитуды). На логарифмической шкале оба графика (и амплитуды и мощности) выглядят идентично и отличаются только коэффициентом — все значения на графике мощности ровно вдвое больше чем на шкале амплитуд. Соответственно для построения графика распределения мощности по частоте (в децибелах) можно не возводить ничего в квадрат, а посчитать десятичный логарифм и умножить его на 20.
Заскучали? Погодите, еще немного, с занудной частью статьи, объясняющей как интерпретировать графики, мы скоро покончим :). Но перед этим следует понять одну крайне важную вещь: хотя все вышеприведенные графики спектров были нарисованы для некоторых ограниченных диапазонов значений (в частности, положительных чисел), все эти графики на самом деле продолжаются в плюс и минус бесконечность. На графиках просто изображается некоторая “наиболее содержательная” часть графика, которая обычно зеркально отражается для отрицательных значений параметра и зачастую периодически повторяется с некоторым шагом, если рассматривать её в более крупном масштабе.
Определившись с тем, что же рисуется на графиках, давайте вернемся собственно к преобразованию Фурье и его свойствам. Существует несколько разных способов как определить это преобразование, отличающихся небольшими деталями (разными нормировками). Например в наших ВУЗах почему-то часто используют нормировку преобразования Фурье определяющую спектр в терминах угловой частоты (радианов в секунду). Я буду использовать более удобную западную формулировку, определяющую спектр в терминах обычной частоты (герцах). Прямое и обратное преобразование Фурье в этом случае определяются формулами слева, а некоторые свойства этого преобразования которые нам понадобятся — списком из семи пунктов справа:
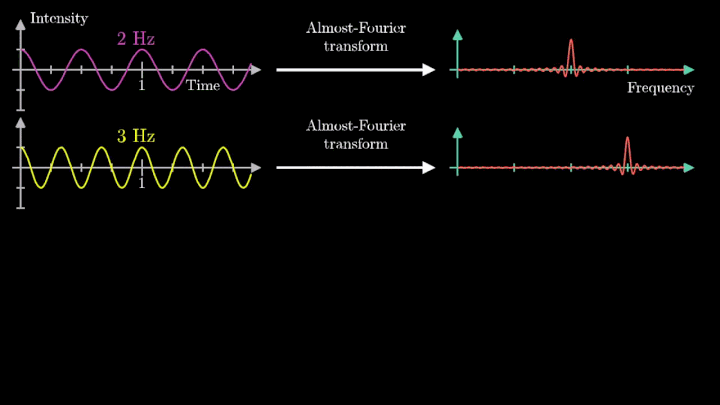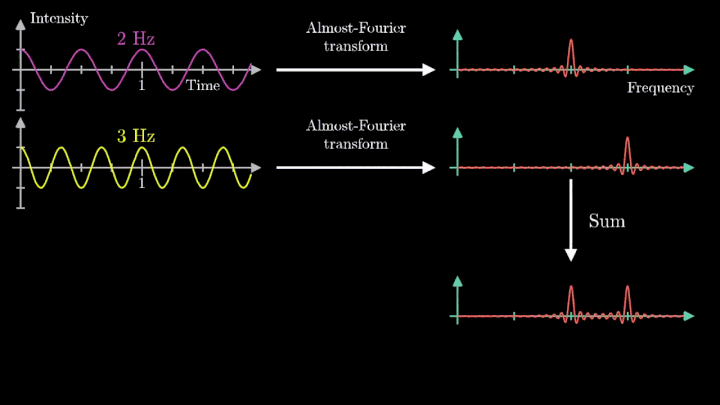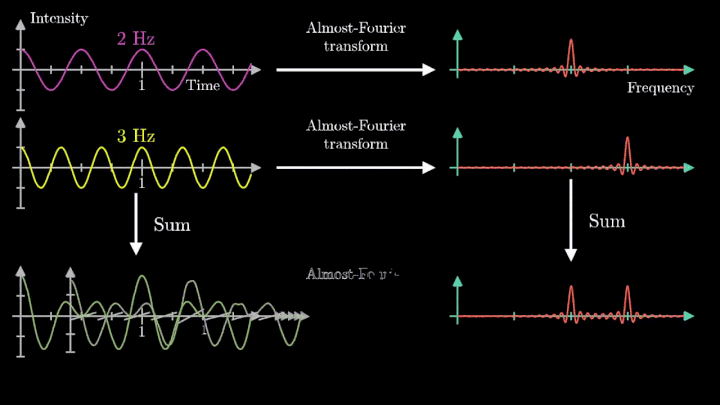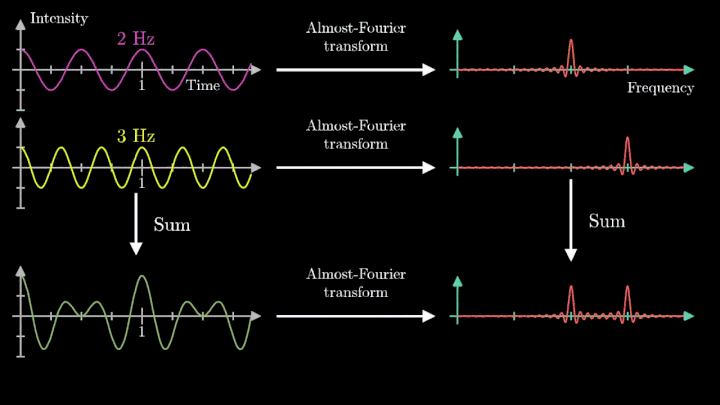
Если взять функцию, состоящую из суммы множества синусоид с разными частотами, то согласно свойству линейности, фурье-образ этой функции будет состоять из соответствующего набора дельта-функций. Это позволяет дать наивную, но наглядную интерпретацию спектра по принципу “если в спектре функции частоте f соответствует амплитуда a, то исходную функцию можно представить как сумму синусоид, одной из которых будет синусоида с частотой f и амплитудой 2a”. Строго говоря, эта интерпретация неверна, поскольку дельта-функция и точка на графике — это совершенно разные вещи, но как мы увидим дальше, для дискретных преобразований Фурье она будет не так уж и далека от истины.
Второе свойство преобразования Фурье — это независимость амплитудного спектра от сдвига сигнала по времени. Если мы подвинем функцию влево или вправо по оси x, то поменяется лишь её фазовый спектр.
Третье свойство — растяжение (сжатие) исходной функции по оси времени (x) пропорционально сжимает (растягивает) её фурье-образ по шкале частот (w). В частности, спектр сигнала конечной длительности всегда бесконечно широк и наоборот, спектр конечной ширины всегда соответствует сигналу неограниченной длительности.
Четвертое и пятое свойства самые, пожалуй, полезные из всех. Они позволяют свести свертку функций к поточечному перемножению их фурье-образов и наоборот — поточечное перемножение функций к свертке их фурье-образов. Чуть дальше я покажу насколько это удобно.
Наконец последнее, седьмое свойство, говорит о том, что преобразование Фурье сохраняет “энергию” сигнала. Оно осмысленно только для сигналов конечной продолжительности, энергия которых конечна, и говорит о том, что спектр подобных сигналов на бесконечности быстро приближается к нулю. Именно в силу этого свойства на графиках спектров как правило изображают только “основную” часть сигнала, несущую в себе львиную долю энергии — остальная часть графика просто стремится к нулю (но, опять же, нулем не является).
Вооружившись этими 7 свойствами, давайте посмотрим на математику “оцифровки” сигнала, позволяющую перевести непрерывный сигнал в последовательность цифр. Для этого нам понадобится взять функцию, известную как “гребенка Дирака”:
Гребенка Дирака — это просто периодическая последовательность дельта-функций с единичным коэффициентом, начинающаяся в нуле и идущая с шагом T. Для оцифровки сигналов, T выбирают по возможности малым числом, T
Преобразование Фурье: самый подробный разбор
Преобразование Фурье – одно из базовых понятий в обработке сигналов и анализе данных. Но что оно означает? Геометрическая интерпретация.
Возьмём классическую задачу – работу со звуком. Теперь добавим конкретики.
Ваш друг приносит запись своего живого выступления. И это очень удачное выступление. Но! Хотя запись делали на хороший микрофон, в ней всё равно присутствует шум. Друг просит помочь убрать его или хотя бы уменьшить.
Здесь и пригодится знание преобразования Фурье.
Что такое звук в математическом смысле?
Отдельная нота – это гармонический сигнал с определённой частотой и амплитудой.
Как правило, мелодию, речь или иной звуковой сигнал можно представить как сумму гармонических сигналов. Шумом в таком случае мы называем слагаемые, соответствующие любым нежелательным звукам.
Преобразование Фурье позволяет разложить исходный сигнал на гармонические составляющие, что потребуется для выделения шумов.
Здесь g(t) – это исходный сигнал (в нашем случае запись друга). В контексте преобразования Фурье его называют оригиналом. G(f) – изображение по Фурье, а параметром f выступает частота.
Возможно, вам уже знакомо это определение. Но знаете ли вы, как происходит это преобразование? Если бы увидели его впервые, поняли бы, как с его помощью анализировать исходный сигнал?
Геометрическая интерпретация преобразования Фурье
Грант Сандерсон предлагает геометрический аналог преобразования Фурье. За несколько графических переходов от исходного сигнала к изображению каждая из компонент определения обретает смысл, а само преобразование получает новое геометрическое прочтение.
В дальнейшем обсуждении предполагается, что вы знакомы с векторами, интегрированием и понятием комплексного числа. Если каких-то знаний вам всё-таки не хватает, ознакомьтесь с материалами из нашей подборки по вузовской математике.
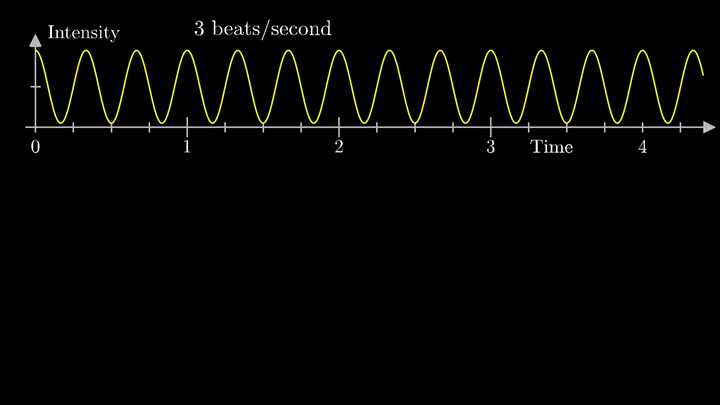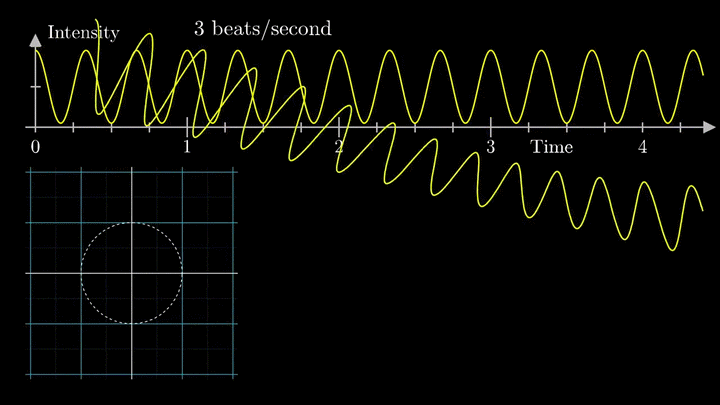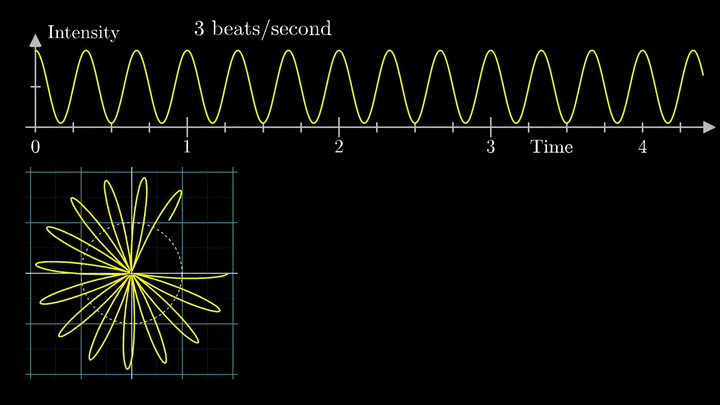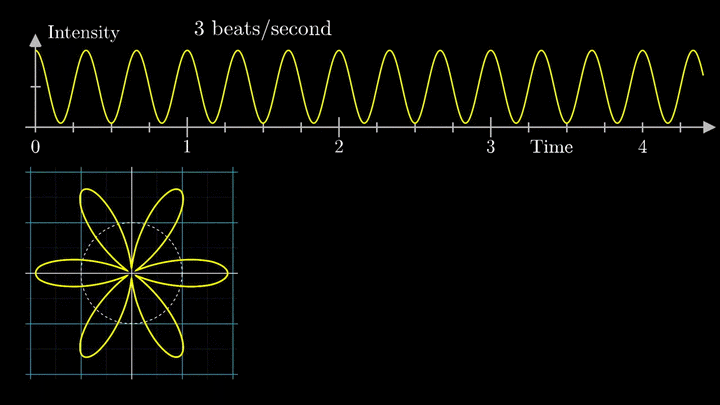
1. Наматываем сигнал
Отобразим g(t) на комплексную плоскость. Для этого введём радиус-вектор, который равномерно вращается по часовой стрелке. Его длина в каждый момент времени равна модулю значения сигнала, а частота вращения выбирается произвольным образом.
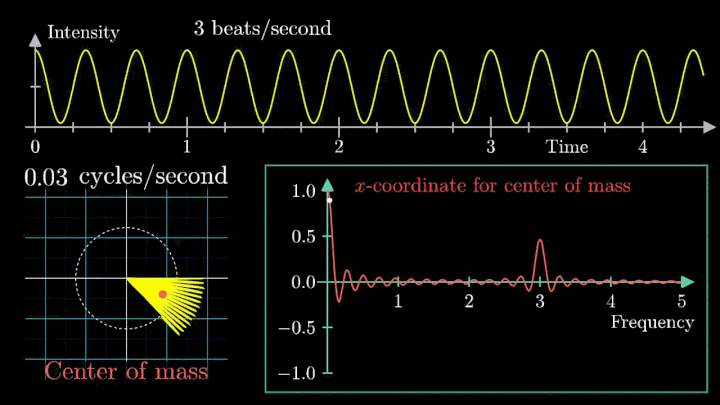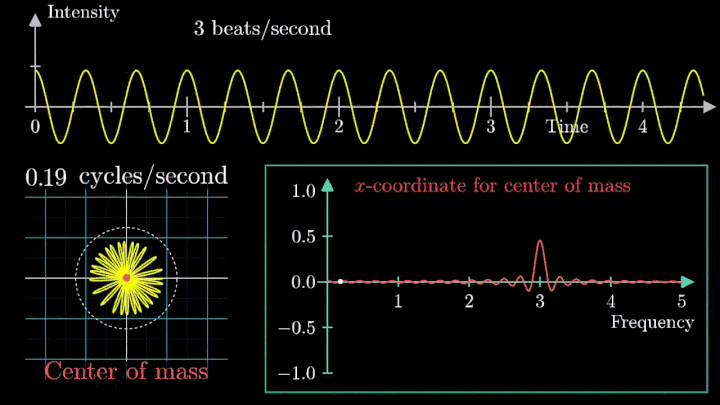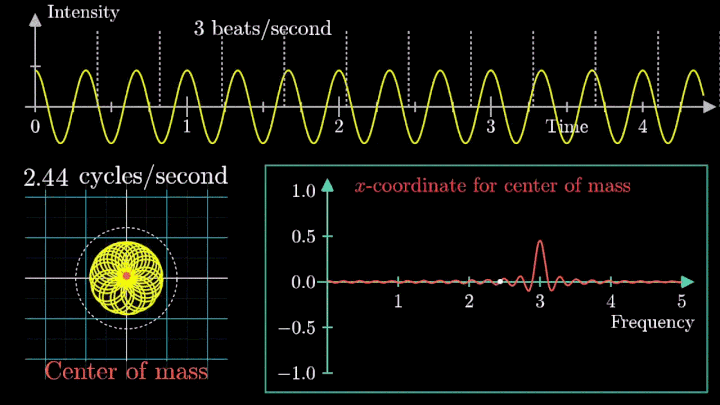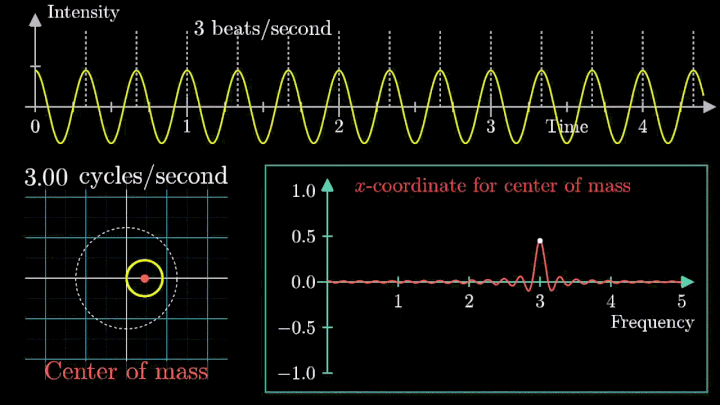
Теперь построим траекторию движения конца вектора, совершающего полный оборот за две секунды, или, другими словами, с частотой вращения fВ = 0.5 об/с.
Выглядит, будто мы намотали исходный сигнал на начало координат. В минимумах сигнала полученная «намотка» сливается с началом координат, а при приближении к максимумам – отклоняется.
Пока выглядит не особо информативно, не так ли?
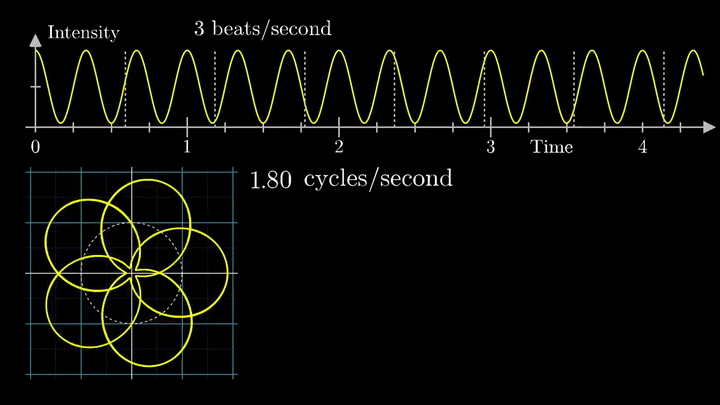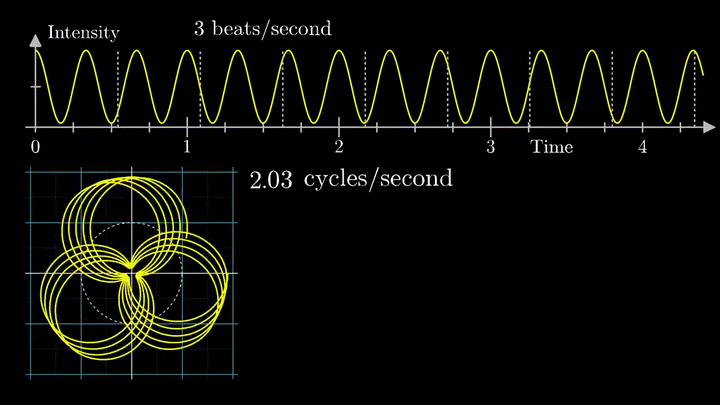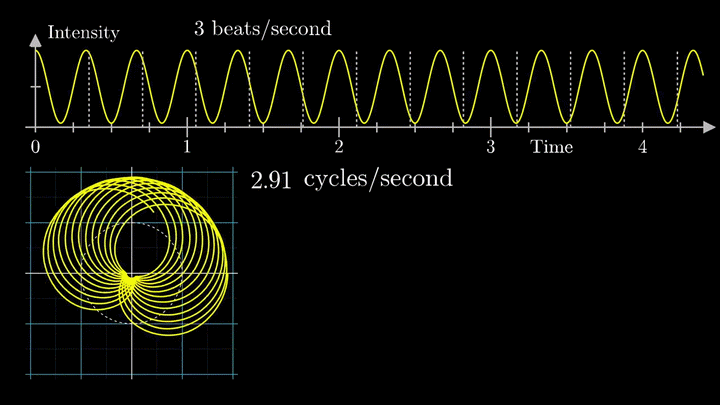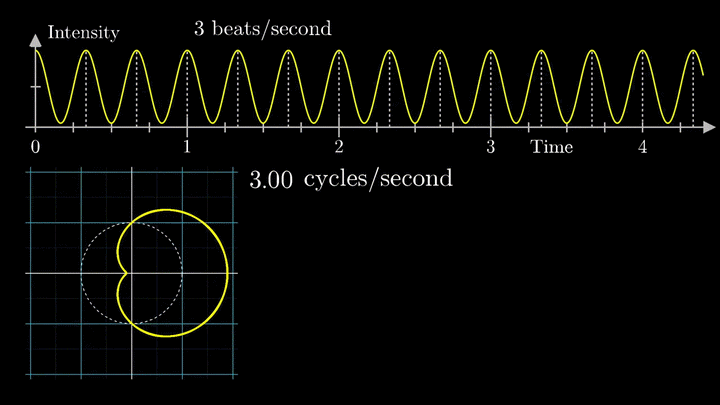
А теперь увеличим частоты намотки.
Сначала график распределяется довольно симметрично относительно начала координат до частоты вращения fВ = 3 об/с. Затем максимумы резко смещаются в правую полуплоскость, а намотка перестаёт напоминать узор спирографа.
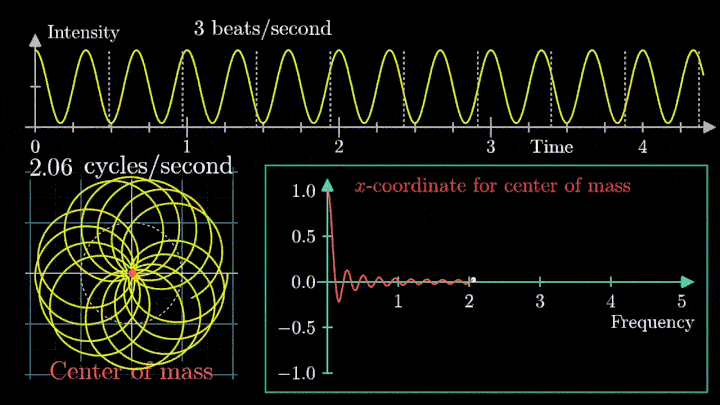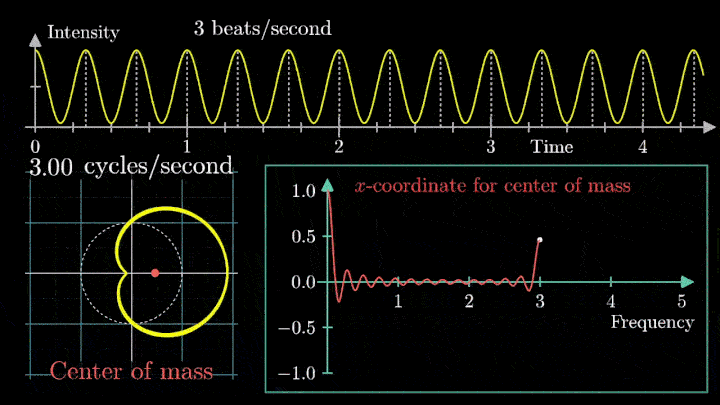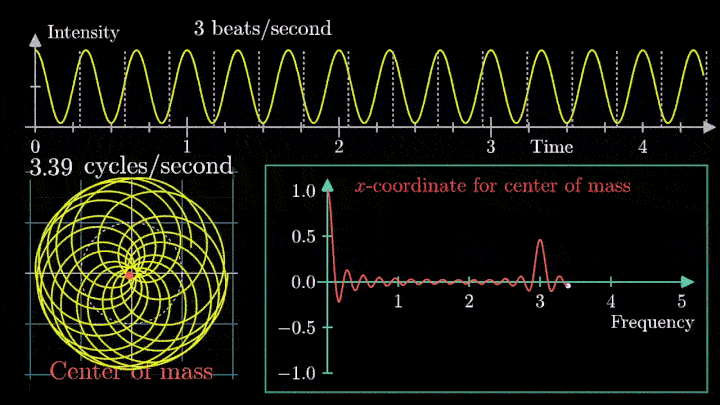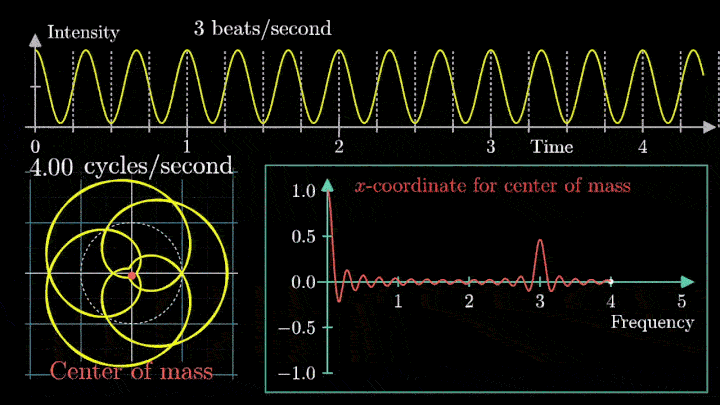
2. Ищем центр масс
Посмотрим внимательнее, что происходит. В качестве характеристики намотки возьмём усреднённое значение всех её точек – центр масс (отметим его оранжевым цветом).
Строим зависимость положения центра масс от частоты намотки. Сейчас нам достаточно рассмотреть х-кординату, но в дальнейшем для определения преобразования Фурье потребуются обе координаты.
Тогда что означает всплеск на низких частотах?
3. Анализируем влияние смещения
Возможно, вы обратили внимание, что рассматриваемый нами сигнал смещён на единицу. Сдвиг был введён для наглядности, но именно он приводит к усложнению поведения центра масс.
При нулевой частоте всё отображение сигнала на комплексной плоскости располагается на оси абсцисс. На малых частотах намотка по-прежнему группируется в правой полуплоскости.
Как только мы убираем сдвиг, т. е. берём сигнал вида g(t) = cos (6πt), намотка при низких частотах сдвигается влево по оси абсцисс.
Построение радиус-вектора остаётся аналогичным. Его длина равна модулю значения сигнала, направление вращения – положительное. Но при смене знака g(t) направление вектора меняется на противоположное.
Сейчас вы увидите, как меняется намотка и х-координата центра масс несмещённого сигнала.
Таким образом, на графике остался только один резкий скачок.
Это важный момент при использовании преобразования Фурье: линейный тренд и смещение проявляются на низких частотах, потому их исключают из исходного сигнала.
4. Выделяем частоты полигармонического сигнала
Мы наблюдаем два пика в точках fВ = 2 об/с и fВ = 3 об/с, что соответствует частотному составу исходной суммы.
Отметим ещё один интересный факт, верный как для х-координаты, так и для преобразования Фурье. Преобразование для суммы сигналов и сумма преобразований сигналов имеют один и тот же вид. Т. е. преобразование Фурье линейно.
Таким образом, этот подход позволяет определить частоту колебаний как моно-, так и полигармонического сигнала. Осталось математически описать процедуру вычисления центра масс намотки.
Вывод преобразования Фурье
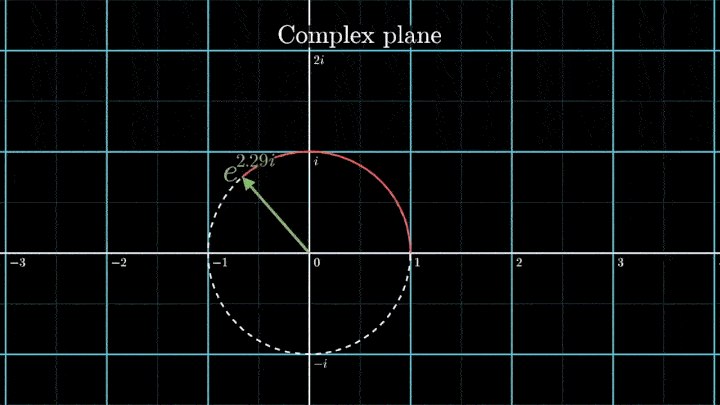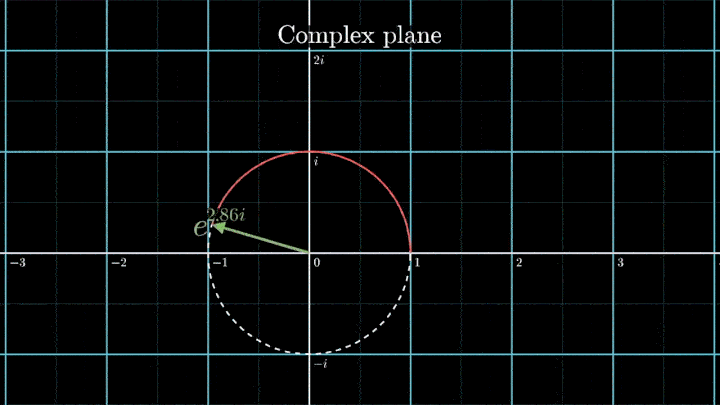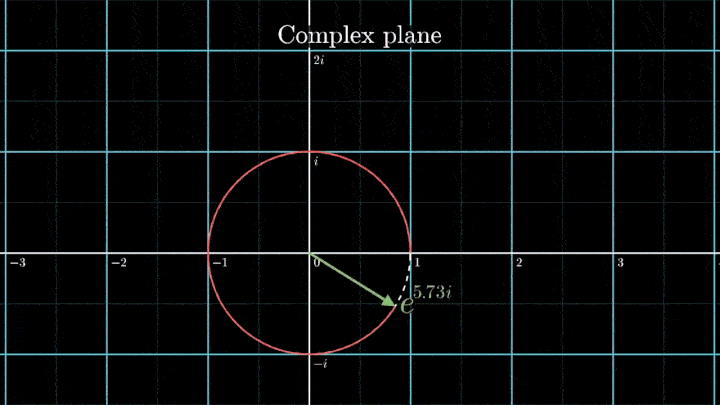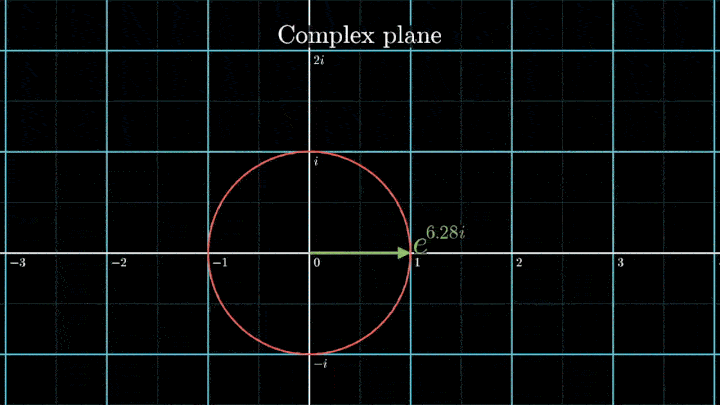
В самом начале рассмотрения мы отобразили исходный сигнал на комплексную плоскость. Такой выбор не случаен – это позволяет рассматривать точки на плоскости как комплексные числа и использовать формулу Эйлера для описания намотки:
Геометрически это соотношение означает, что при любом φ точка e iφ на комплексной плоскости лежит на единичной окружности.
Построим радиус-вектор e iφ при разных значениях φ.
При изменении φ на 2π вектор проходит полный оборот против часовой стрелки, так как 2π – длина единичной окружности. Чтобы задать скорость вращения вектора, показатель степени домножаем на ft, а для смены направления вращения – на -1.
Теперь вычисляем центр масс. Для этого отметим N произвольных точек на графике намотки и вычислим среднее:
Если мы будем увеличивать количество рассматриваемых точек, придём к предельному случаю:
где t1 и t2 – границы интервала, на котором рассматривается сигнал.
Выражение перед интегралом представляет собой масштабирующий коэффициент, но не отражает поведение центра масс. Потому его можно отбросить.
Полученное выражение и будет являться преобразованием Фурье с той разницей, что в общем виде интегрирование задаётся на интервале от -∞ до +∞.
Такой переход к бесконечному интервалу означает, что мы не накладываем никаких ограничений на длительность рассматриваемого сигнала.
Применение преобразования Фурье для фильтрации
Теперь, говоря о преобразовании Фурье, вы можете представлять его геометрическую интерпретацию – намотку сигнала на комплексную плоскость и вычисление центр масс.
При этом частота намотки f становится входным параметром для изображения по Фурье. Центр масс выступает оценкой, насколько хорошо соотносится (коррелирует) параметр f с присутствующими в сигнале частотами.
После того, как вы найдёте в принесённой другом записи все частотные компоненты, вам останется только вычесть их из изображения и применить обратное преобразование Фурье.