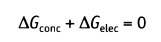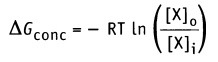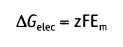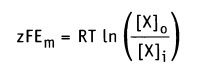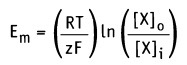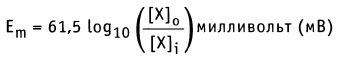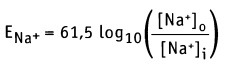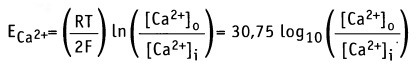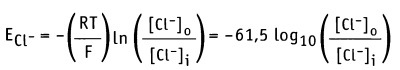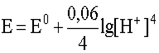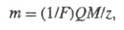Для чего нужно уравнение нернста
Вывод уравнения Нернста



Электродные потенциалы. Электрод. Абсолютный и относительный электродный потенциалы. Водородная шкала относительных электродных потенциалов. Факторы, влияющие на величину относительного электродного потенциала (уравнение Нернста).
Электродный потенциал — разность электрических потенциалов между электродом и находящимся с ним в контакте электролитом (чаще всего между металлом и раствором электролита). Возникновение электродного потенциала обусловливается переносом заряженных частиц через границу раздела фаз, специфической адсорбцией ионов, а при наличии полярных молекул (в том числе молекул растворителя) — ориентационной адсорбцией их. Величина электродного потенциала в неравновесном состоянии зависит как от природы и состава контактирующих фаз, так и от кинетических закономерностей электродных реакций на границе раздела фаз.
Положительный электрод – анод.
Отрицательный электрод – катод.
Если электродная реакция, записанная в сторону восстановления, является самопроизвольной, то потенциал электрода положителен.
Уравнение Нернста — уравнение, связывающее окислительно-восстановительный потенциал системы с активностями веществ, входящих в электрохимическое уравнение, и стандартными электродными потенциалами окислительно-восстановительных пар.
Вывод уравнения Нернста
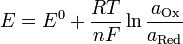
Если в формулу Нернста подставить числовые значения констант 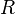
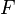
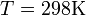
Научная электронная библиотека
Таланов В. М., Житный Г. М.,
1.3.2. Уравнение Нернста и его различные формы
Окислительно-восстановительной системе, записанной в общем виде
соответствует наиболее общая форма уравнения Нернста:
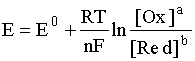
Если заменить натуральный логарифм десятичным и подставить соответствующие значения постоянных величин в предлогарифмическом сомножителе, то для температуры 298 К уравнение имеет вид
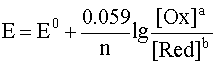
В дальнейшем будем пользоваться округленным значением числовой константы в логарифмическом слагаемом, что значительно упрощает расчеты, не внося в их результат существенной ошибки:
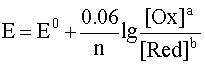
Например, для полуреакции
уравнение Нернста имеет вид:
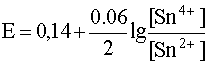
В различных частных случаях, в зависимости от характера полуреакции, уравнение Нернста записывается по-разному:
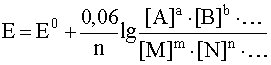
Например, для окислительно-восстановительной системы
потенциал выражается уравнением
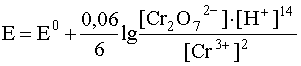
2. Если окислительно-восстановительная система включает в себя малорастворимое вещество, то его концентрация, будучи также величиной постоянной, не включается в логарифмический член уравнения Нернста. Так, для полуреакции
уравнение Нернста имеет вид
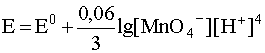
3. Для металлических электродов, то есть для окислительно-восстановительных систем, представляющих собой металл, контактирующий с раствором, содержащим катионы этого же металла, например, для электрода
уравнение Нернста включает только концентрацию катионов металла в растворе, то есть
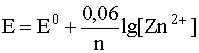
4. Если окислительно-восстановительная система включает в себя малорастворимый в воде газ (H2, O2, N2 и т.д.), то в уравнение Нернста входит не концентрация этого газа, а его парциальное давление. Например, для системы
уравнение Нернста должно быть записано следующим образом:
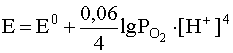
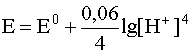
Применение уравнения Нернста в решении задач.
При рассмотрении вопроса об окислительно-восстановительных реакциях часто возникает необходимость расчета электродвижущей силы (ЭДС) и потенциалов отдельных полуреакций. В справочниках обычно приведены таблицы т.н. стандартных потенциалов тех или иных процессов, рассчитанных при р=1 атм, Т=298К и активностях участников равных 1. Однако в реальных задачах условия могут значительно отличаться от указанных выше. Как быть в таком случае? Ответ дает уравнение Нернста. В оригинальном виде оно выглядит так:
Как можно заметить, в уравнении фигурируют несколько постоянных величин. Также температура в подавляющем большинстве случаев равна 298К. Кроме того, можно заменить натуральный логарифм на десятичный. Это можно сделать путем умножения на коэффициент перевода. Если собрать все постоянные в единый множитель, то приходим к несколько иному, но более знакомому по учебным пособиям виду уравнения Нернста:
Такой вариант уравнения сильно облегчает жизнь в ряде случаев, например рассмотрении рН-зависимых процессов. Используя данное уравнение можно провести вычисления в любых условиях, приведенных в задаче. Рассмотрим характерные примеры задания по данной теме.
Пример 1:
Рассчитать ЭДС гальванического элемента, составленного из медной и цинковой пластин, погруженных в растворы 0.1М CuSO4 и 0.01М ZnSO4 соответственно. Коэффициенты активности ионов Cu 2+ и Zn 2+ принять равными единице.
Решение:
Для начала запишем уравнения протекающих процессов:
Далее находим по таблице стандартные потенциалы процессов:
Если в условиях задачи ничего не сказано про коэффициенты активности ионов, то можно считать их равными единице, как и в нашем случае. Тогда активности участников процессов можно принять равными их аналитическим концентрациям.
Найдем реальные потенциалы с учетом нестандартных активностей ионов:
Далее необходимо сравнить полученные величины между собой, чтобы определить, кто из участников процесса – окислитель. Потенциал меди больше, чем у цинка, поэтому она будет окислителем. Тогда найдем ЭДС системы:
Ответ: 1.13 В
Пример 2:
Одним из лабораторных способов получения хлора является действие KMnO4 на концентрированную соляную кислоту. Можно ли провести процесс при рН=4?
Решение:
Для начала запишем уравнения протекающих процессов.
Далее находим по таблице стандартные потенциалы процессов:
Несложно заметить, что от рН в данном случае зависит только потенциал перманганата. Тогда воспользуемся уравнением Нернста и рассчитаем его реальный потенциал в условиях задачи:
Получается, что потенциал KMnO4 стал меньше, чем у хлора, а значит, реакция не пойдет.
Для чего нужно уравнение нернста
Равновесие между химическими и электрическими движущими силами определяет величину мембранного потенциала покоя. Состояние равновесия достигается, когда различие в свободной энергии этих сил равно нулю (другими словами, когда общий поток = 0):
Изменение свободной энергии, происходящее при движении через мембрану компонента X, можно выразить уравнением:
• R — газовая постоянная (2 кал моль-1 К-1)
• Т — абсолютная температура (К; 37 °С = 307,5 К)
• [Х]0 — концентрация X вне клетки
• [X]i — концентрация X внутри клетки
и изменение свободной энергии, обусловленное транспортом через мембрану заряда, связанного с растворенным компонентом X составляет:
• Em — равновесный потенциал (в вольтах)
• z — валентность иона (электрический заряд)
• F— число Фарадея (2,3 х 104 кал вольт-1 моль-1)
В состоянии равновесия
и после преобразования получаем.
Таким образом, значение равновесного потенциала или потенциала Нернста для одновалентного иона X при 37 °С определяется уравнением:
Почти во всех покоящихся клетках млекопитающих плазматическая мембрана проницаема для ионов К+. Na+/К+-АТФаза поддерживает трансмембранный ионный градиент и создает внутри клетки относительно высокую концентрацию ионов К+ ([K+]i). При открытии некоторых К+-каналов ионы К+ начинают транспортироваться в направлении градиента концентрации, что приводит к появлению положительного заряда с внешней стороны мембраны и отрицательного с внутренней ее стороны. Этот отрицательный мембранный потенциал, Еm, представляет собой электродвижущую силу, которая препятствует дальнейшему выходу К+ из клетки в направлении градиента (химическая движущая сила). Таким образом, открытие в покоящейся клетке специальных селективных К+-каналов определяет значение отрицательного потенциала покоя, при котором не происходит транспорта К+ через мембрану и величина Еm остается постоянной.
Аналогично потенциал Нернста можно рассчитать и для других ионов. Если мембрана становится более проницаемой для определенных ионов, то мембранный потенциал Еm будет меняться, приближаясь к значению потенциала Нернста для этих ионов (обычно становясь более положительным при деполяризации мембраны).
Если [Na+]0 = 145 мМ и [Na+]i = 12 мМ (как для клеток мышц), то значение мембранного потенциала составляет Еm = +67 мВ, принимая во внимание транспорт только ионов Na+. Таким образом, суммарный эффект открытия Na+ каналов выражается в установлении потока ионов натрия, направленного в клетку, что приводит к сдвигу отрицательного потенциала покоя Еm до значения +67 мВ.
Аналогичным образом, когда плазматическая мембрана становится более проницаемой для Са2+, ионы транспортируются в направлении градиента концентрации. При этом мембрана на внешней стороне приобретает более отрицательный заряд, а на внутренней — более положительный. Когда под действием электрического заряда клетка возбуждается и открываются Са2+-каналы, теоретическое равновесие между потоком Са2+ в клетку и потоком К+ из клетки определяет уровень мембранного потенциала ближе к значению ЕCa. Согласно уравнению Нернста,
Если [Са2+]0 = 1,5 мМ и [Ca2+]i = 0,1 мкМ, как для мышечной клетки, то мембранный потенциал составляет Em = +129 мВ. Таким образом, суммарный эффект открытия Са2+ каналов выражается в установлении потока Са2+ в клетку, который приводит к сдвигу отрицательного потенциала покоя Еm, к +129 мВ. [Са2+-каналы открываются при более положительном значении потенциала действия, чем натриевые каналы. Это означает, что они открываются на более поздней фазе потенциала действия. Для ионов Cl_ по уравнению Нернста получаем
Редактор: Искандер Милевски. Дата обновления публикации: 18.3.2021
Уравнение Нернста и его различные формы



Окислительно-восстановительной системе, записанной в общем виде
соответствует наиболее общая форма уравнения Нернста:
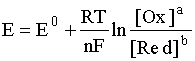
Если заменить натуральный логарифм десятичным и подставить соответствующие значения постоянных величин в предлогарифмическом сомножителе, то для температуры 298 К уравнение имеет вид
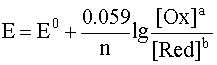
В дальнейшем будем пользоваться округленным значением числовой константы в логарифмическом слагаемом, что значительно упрощает расчеты, не внося в их результат существенной ошибки:
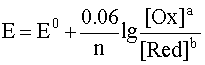
Например, для полуреакции
уравнение Нернста имеет вид:
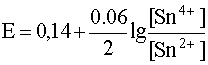
В различных частных случаях, в зависимости от характера полуреакции, уравнение Нернста записывается по-разному:
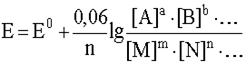
Например, для окислительно-восстановительной системы
потенциал выражается уравнением
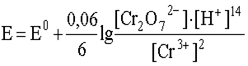
2. Если окислительно-восстановительная система включает в себя малорастворимое вещество, то его концентрация, будучи также величиной постоянной, не включается в логарифмический член уравнения Нернста. Так, для полуреакции
уравнение Нернста имеет вид
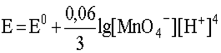
3. Для металлических электродов, то есть для окислительно-восстановительных систем, представляющих собой металл, контактирующий с раствором, содержащим катионы этого же металла, например, для электрода
уравнение Нернста включает только концентрацию катионов металла в растворе, то есть
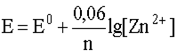
4. Если окислительно-восстановительная система включает в себя малорастворимый в воде газ (H2, O2, N2 и т.д.), то в уравнение Нернста входит не концентрация этого газа, а его парциальное давление. Например, для системы
уравнение Нернста должно быть записано следующим образом:
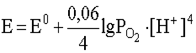
Ряд напряжений характеризует сравнительную активность металлов в окислительно-восстановительных реакциях в водных растворах.
| Li→Rb→K→Ba→Sr→Ca→Na→Mg→Al→Mn→Cr→Zn→Fe→Cd→Co→Ni→Sn→Pb→H→Sb→Bi→Cu→Hg→Ag→Pd→Pt→Au |
30.Схема гальванического элемента
На аноде протекает процесс окисления цинка:
В результате этого атомы цинка превращаются в ионы, которые переходят в раствор, а цинковый анод растворяется, и его масса уменьшается. Обратите внимание, что анод в гальваническом элементе является отрицательным электродом (за счет электронов, полученных от атомов цинка) в отличие от процесса электролиза, где он подключается к положительном полюсу внешней батареи.
Электроны от атомов цинка по внешней электрической цепи (металлическому проводнику) движутся к катоду, где протекает процесс восстановления ионов меди из раствора ее соли:
В результате этого образуются атомы меди, которые осаждаются на поверхности катода, и его масса увеличивается. Катодом в гальваническом элементе является положительно заряженный электрод.
Суммарное уравнение реакции, протекающей в медно-цинковом гальваническом элементе, можно представить так:
Zn + Cu 2+ = Zn 2+ + Cu.
31. Гальванический элемент. ЭДС гальванического элемента
Рассмотрим простейший гальванический элемент Даниэля – Якоби, состоящий из двух полуэлементов – цинковой и медной пластин, помещенных в растворы сульфатов цинка и меди соответственно, которые соединены между собой посредством электролитического ключа – например, полоски бумаги, смоченной раствором какого-либо электролита. Схематически данный элемент изображается следующим образом:
Zn / Zn 2+ // Cu 2+ / Cu
На поверхности каждого из электродов имеет место динамическое равновесие перехода ионов металла из электрода в раствор и обратно, характеризуемое потенциалом ДЭС (зарядом на электроде q). Если соединить медный и цинковый электроды металлическим проводником, немедленно произойдет перераспределение зарядов – электроны начнут перемещаться с электрода с более отрицательным зарядом (в нашем случае – цинкового) на электрод с более положительным зарядом (медный), т.е. в проводнике возникнет электрический ток. Изменение величины заряда каждого из электродов нарушает равновесие – на цинковом электроде начнется процесс перехода ионов из электрода в раствор (окисление металла), на медном – из раствора в электрод (восстановление металла); при этом протекание процесса на одном электроде обусловливает одновременное протекание противоположного процесса на другом:
Электрод, на котором при работе гальванического элемента протекает процесс окисления, называется анодом, электрод, на котором идет процесс восстановления – катодом. При схематическом изображении гальванических элементов слева записывают анод, справа – катод (стандартный водородный электрод всегда записывают слева). Суммарный окислительно-восстановительный процесс, происходящий в гальваническом элементе, выражается следующим уравнением:
Сu 2+ + Zn o ––> Сu o + Zn 2+
Т.о., гальванический элемент можно определить как прибор для преобразования химической энергии окислительно-восстановительной реакции в электрическую за счет пространственного разделения процессов окисления и восстановления. Работа, которую может совершить электрический ток, вырабатываемый гальваническим элементом, определяется разностью электрических потенциалов между электродами (называемой обычно просто разностью потенциалов) ΔΦ и количеством прошедшего по цепи электричества q:
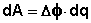
Работа тока гальванического элемента (и, следовательно, разность потенциалов), будет максимальна при его обратимой работе, когда процессы на электродах протекают бесконечно медленно и сила тока в цепи бесконечно мала. Максимальная разность потенциалов, возникающая при обратимой работе гальванического элемента, есть электродвижущая сила (ЭДС) гальванического элемента.
32. Электролиз. Последовательность разрядов ионов на электродах. Явление перенапряжения. Электролиз с растворимыми и нерастворимыми электродами.
Из растворов солей химически активные Ме, стоящие в ряду стандартных потенциалов до аллюминия включительно, на электроде не восстанавливаются, а восстанавливаются ионы водорода. На катоде легче всего восстанавливаются ионы менее активныхМе, стоящих в РСП после водорода. Из растворов солей Ме, которые расположены между аллюминием и водородом, восстанавливаются, но и возможно восстановление ионов водорода.
Процессы, протекающие при электролизе обратны процессам, идущим при работе гальвонического элемента: при электролизе химическоя реакция осуществляется за счёт энергии электрического тока, подводимой извне, в то время как при работе гальванического элемента энергия самопроизвольно протекающей в нём химической реакции превращается в электрическую энергию. Таким образом при электролизе возникает ГЭ (зарядка).
Существует таблица перенапряжений. Перенапряжением выделения водорода называется смещение или сдвиг потенциала выделения водорода в сторону более отрицательных значений при при его выделении на данном материале по сравнению с выделением его на чернёной платине.
В цветной металлургии электролиз используется для извлечения металлов из руд и их очистки. Электролизом расплавленных сред получают алюминий, магний, титан, цирконий, уран, бериллий и др.
Для рафинирования (очистки) металла электролизом из него отливают пластины и помещают их в качестве анодов в электролизер. При пропускании тока металл, подлежащий очистке, подвергается анодному растворению, т. е. переходит в раствор в виде катионов. Затем эти катионы металла разряжаются на катоде, благодаря чему образуется компактный осадок уже чистого металла. Примеси, находящиеся в аноде, либо остаются нерастворимыми, либо переходят в электролит и удаляются.
Гальванотехника – область прикладной электрохимии, занимающаяся процессами нанесения металлических покрытий на поверхность как металлических, так и неметаллических изделий при прохождении постоянного электрического тока через растворы их солей. Гальванотехника пожразделяется на гальваностегию и гальванопластику.
Гальваностегия (от греч.покрывать) – это электроосаждение на поверхность металла другого металла, который прочно связывается (сцепляется) с покрываемым металлом (предметом), служащим катодом электролизера.
Перед покрытием изделия необходимо его поверхность тщательно очистить (обезжирить и протравить), в противном случае металл будет осаждаться неравномерно, а кроме того, сцепление (связь) металла покрытия с поверхностью изделия будет непрочной. Способом гальваностегии можно покрыть деталь тонким слоем золота или серебра, хрома или никеля. С помощью электролиза можно наносить тончайшие металлические покрытия на различных металлических поверхностях. При таком способе нанесения покрытий, деталь используют в качестве катода, помещенного в раствор соли того металла, покрытие из которого необходимо получить. В качестве анода используется пластинка из того же металла.
Гальванопластика– получение путем электролиза точных, легко отделяемых металлических копий относительно значительной толщины с различных как неметаллических, так и металлических предметов, называемых матрицами.
С помощью гальванопластики изготовляют бюсты, статуи и т. д.
Гальванопластика используется для нанесения сравнительно толстых металлических покрытий на другие металлы (например, образование «накладного» слоя никеля, серебра, золота и т. д.).
34. Фарадея законы, основные законы электролиза, отражающие общий закон сохранения вещества в условиях протекания электрохимической реакции. Установлены M. Фарадеем в 1833-34.
Согласно 2-му закону, для разных электродных процессов при одинаковом количестве пропущенного электричества Q массы прореагировавших веществ относятся друг к другу так же, как эквиваленты химические этих веществ. Оба закона Фарадея объединяются одним уравнением:
Законы Фарадея законы относятся к числу строгих законов, но в ряде случаев могут наблюдаться кажущиеся отклонения от них, вызываемые следующими причинами:
1) в нестационарных условиях электролиза часть электричества затрачивается на заряжение двойного электрического слоя.
2) если электролит обладает электронной проводимостью (например, раствор металлического Na в жидком аммиаке), то часть тока через электролит переносят электроны, а не ионы, и соответствующее количество электричества не участвует в процессе электролиза;
3) наряду с основным процессом электролиза, например образованием металлического Zn по реакции Zn 2+ + 2е 
Законы Фарадея законы сыграли важную роль в понимании природы химической связи и развития атомно-молекулярной теории. Их используют при выводе всех уравнений, описывающих электрохимические превращения веществ на границах раздела проводников 1-го и 2-го рода. Практическое применение законы Фарадея законы находят в кулонометрии, а также при определении выхода реакции по току, то есть отношения теоретического количества электричества, рассчитанного на основе законов Фарадея законы, к количеству электричества, реально затраченному на получение данного вещества в процессе электролиза.