Для чего нужно знать характеристики упругих свойств материалов

Упругие свойства материала. Обобщенный закон Гука. Методы определения модуля упругости. Ферромагнитная аномалия упругости

Страницы работы

Фрагмент текста работы

9. УПРУГИЕ СВОЙСТВА МАТЕРИАЛА

Под упругостью понимают способность материала восстанавливать первоначальную форму и размеры после снятия внешних механических нагрузок. Упругость, также как и другие физические свойства, может быть использована для исследования металлов и сплавов при решении задач материаловедения.

Основными количественными характеристиками упругости являются модуль нормальной упругости (Е), модуль сдвига (G) и модуль объемной упругости или модуль всестороннего сжатия (D), вычисляемые как первая производная изменения степени линейной, угловой и объемной деформации от приложенной внешней нагрузки в области проявления закона Гука. Все три модуля упругости связаны между собой соотношениями

(9.1)

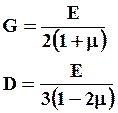
где μ – коэффициент Пуассона.

Коэффициент Пуассона характеризует изменение объема тела при упругой деформации. При одноосном растяжении образца квадратного сечения увеличение объема вследствие его удлинения частично компенсируется поперечным сужением. Аналогичные процессы, но с противоположным знаком происходят при одноосном сжатии. Коэффициент Пуассона в этом случае определяется

(9.2)

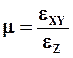
где ε_Z, ε_XY – относительное изменение продольных и поперечных размеров образца

Для большинства металлов и сплавов коэффициент Пуассона находится в пределах 0,25…0,35; наименьшее значение найдено для Be (μ = 0.039), а наибольшее у Pb (μ = 0,44), Tl и In (μ = 0,46).

Для большинства металлов и сплавов выполняется соотношение

…0,382 (9.3)

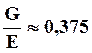
Упругие свойства определяются силами связей между соседними элементарными частицами в материале (атомами или ионами). Рассмотрим, как изменяется потенциальная энергия пары соседних частиц U в зависимости от разделяющего их расстояния r (рис.9.1). Равновесное расстояние между частицами r₀ соответствует минимуму потенциальной энергии. Этот минимум образуется в результате уравновешивания энергий отталкивания и притяжения между двумя соседними атомами или ионами.

Рис. 9.1. Изменение потенциальной энергии (а) и силы (б) взаимодействия от расстояния между атомами (или ионами) материала

Уравнение потенциальной энергии задается выражением

(9.4)

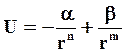
где первое слагаемое описывает энергию притяжения, а второе – энергию отталкивания. В точке r₀ расстояние между частицами соответствует равновесному состоянию, при котором потенциальная энергия достигает минимума. Сила взаимодействия между частицами определяется

(9.5)

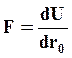
В точке r₀ сила, действующая на частицы равна нулю.

Первая производная от силы по расстоянию, разделяющему частицы, описывает жесткость или обоюдное сопротивление частиц разделению друг от друга

(9.6)

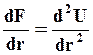
Выражение (9.6) представляет аналог модуля Юнга, который в упругой области пропорционален второму слагаемому, т.е.

(9.7)

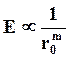
Следовательно, модуль упругости определяется равновесным расстоянием между частицами. С повышением температуры значение r₀ возрастает, приводя к уменьшению модуля упругости.

Поскольку модуль упругости Е зависит от прочности сил межатомной связи, которые изменяются только сообразно типу взаимодействия частиц в том или ином конкретном материале, этот параметр практически не чувствителен к изменениям микроструктуры. Этот факт находит экспериментальное подтверждение. Так, если термообработкой и легированием можно сильно изменить структуру и повысить прочность стали на один порядок и более, то модуль упругости при этом возрастает всего на 5…10%.

9.2. Обобщенный закон Гука

Закон Гука можно обобщить для случая многоосного нагружения, как изотропного, так и анизотропного материала. Напряжение, действующее в одном направлении (допустим вдоль оси Y) вызовет

Источник

Определение характеристик упругих свойств материалов

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: силы в механике, сила упругости, закон Гука.

Как мы знаем, в правой части второго закона Ньютона стоит равнодействующая (то есть векторная сумма) всех сил, приложенных к телу. Теперь нам предстоит изучить силы взаимодействия тел в механике. Их три вида: сила упругости, гравитационная сила и сила трения. Начинаем с силы упругости.

Деформация.

Силы упругости возникают при деформациях тел. Деформация — это изменение формы и размеров тела. К деформациям относятся растяжение, сжатие, кручение, сдвиг и изгиб. Деформации бывают упругими и пластическими. Упругая деформация полностью исчезает после прекращения действия вызывающих её внешних сил, так что тело полностью восстанавливает форму и размеры. Пластическая деформация сохраняется (быть может, частично) после снятия внешней нагрузки, и тело уже не возвращается к прежним размерам и форме.

Частицы тела (молекулы или атомы) взаимодействуют друг с другом силами притяжения и отталкивания, имеющими электромагнитное происхождение (это силы, действующие между ядрами и электронами соседних атомов). Силы взаимодействия зависят о расстояний между частицами. Если деформации нет, то силы притяжения компенсируются силами отталкивания. При деформации изменяются расстояния между частицами, и баланс сил взаимодействия нарушается.

Например, при растяжении стержня расстояния между его частицами увеличиваются, и начинают преобладать силы притяжения. Наоборот, при сжатии стержня расстояния между частицами уменьшаются, и начинают преобладать силы отталкивания. В любом случае возникает сила, которая направлена в сторону, противоположную деформации, и стремится восстановить первоначальную конфигурацию тела.

Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Сила упругости:

1. действует между соседними слоями деформированного тела и приложена к каждому слою; 2. действует со стороны деформированного тела на соприкасающееся с ним тело, вызывающее деформацию, и приложена в месте контакта данных тел перпендикулярно их поверхностям (типичный пример — сила реакции опоры).

Силы, возникающие при пластических деформациях, не относятся к силам упругости. Эти силы зависят не от величины деформации, а от скорости её возникновения. Изучение таких сил выходит далеко за рамки школьной программы.

В школьной физике рассматриваются растяжения нитей и тросов, а также растяжения и сжатия пружин и стержней. Во всех этих случаях силы упругости направлены вдоль осей данных тел.

Упругость, пластичность и вязкость материалов

Реологические свойства материалов (упругость, пластичность и вязкость) описывают характером зависимости напряжения от деформации. Под деформацией

понимается изменение формы и (или) объема тела без нарушения его сплошности.

про­цесс непрерывного роста деформации во времени без увеличения нагрузки. Деформации бывают обратимыми (исчезающими после снятия нагрузки) и необратимыми (остаточными или пластиче­скими).

Обратимыми являются упругие и эластические деформации. Их природа различна. Упругие деформации обусловлены изменением расстояния между атомами, а эластические — изменением конформации макромолекул полимеров. Остаточные деформации в кристаллических телах возникают в результате скольжения дислокаций за счет последовательного перескока ато­мов со своего места на соседнее. Это приводит к необратимому смещению одних частей кристалла по отношению к другим час­тям.

Любую деформацию, независимо от того, происходит она при растяжении, сжатии, изгибе или кручении, можно разложить на две составляющие: изменение объема и изменение формы. При всестороннем равномерном сжатии или растяжении все материа­лы ведут себя одинаково — как упругие тела. Следовательно, по характеру деформации объема тела неразличимы. Изменение же формы в зависимости от нагрузки определяется тремя фундамен­тальными свойствами, присущими всем без исключения матери­алам: упругостью, пластичностью и вязкостью.

Каждое из этих свойств в отдельности описывают законом по­ведения некоторого идеального тела, эквивалентом которого мо­жет служить механическая модель.

это деформация сдвига у, кото­рая равна отношению смещения двух точек элемента вдоль оси
х
к расстоянию между ними по оси
у.
Закон упругости Гука.Закон упругости Гука — это закон пря­мой пропорциональности между напряжением и деформацией, характерный для идеально упругого тела, моделью которого явля­ется спиральная пружина (рис. 2.9, б, в): х = Gy; G =

tga, где С — модуль упругости при сдвиге, равный тангенсу угла наклона гра­фика зависимости х = /(у). Модуль упругости зависит только от свойств данного материала и является одной из его характерис­тик.

Закон пластичности Сен-Венана — Кулона.Деформация идеаль­но пластичного тела отсутствует (у = 0) при напряжениях сдвига меньше предела текучести (х Читайте также: Как сделать станок для лего кирпича своими руками: чертежи и схемы

Коэффициент жёсткости зависит не только от материала пружины, но также от её формы и размеров.

Из формулы (1) следует, что график зависимости силы упругости от (малой) деформации является прямой линией (рис. 1 ):

Назначение, классификация, основные свойства и материалы упругих элементов

Стержень УП имеет следующее. Пружина кручения натяжения (рис. 10.1, а) и сжатия (рис. 10.1, б). Проволока скручивается при деформации пружины. Пружина кручения (рис. 10.1, г) и листовая рессора (рис. 10.1, в, д). Эти материалы подвержены деформации изгиба. Материалы Shell UE испытывают сложные деформации.Плоская и гофрированная мембрана (рис. 10.1 г); мембранная коробка (рис. 10.1, ч); трубчатая пружина (рис. 10.1 а). В зависимости от назначения упругие элементы делятся на силовые, измерительные и упругие струнные элементы.

Эти элементы включают в себя следующее: Гофрированные сильфонные трубки (рис. 10.1, д). Людмила Фирмаль

Силовые УП используются для силового замыкания кинематических пар, необходимых для возврата звеньев фрикционных зажимов, кулачкового и храпового механизма, муфт, движущихся частей механизма в исходное положение или для их приведения в движение (пружинный двигатель) Механическое накопление энергии. Измерительное оборудование используется в манометрах, динамометрах, термометрах и электрических измерительных приборах в качестве чувствительного элемента устройства для измерения давления, силы, силовых моментов, температуры и других параметров. Во многих случаях функция измерительного элемента сочетается с функцией токоподвода.

Тонкие винтовые и винтовые пружины используются в качестве подающих электропитание УП. Эластичный соединительный элемент заменяет жесткое соединение детали на эластичное (эластичное соединение, см. §12.2) в качестве резинового амортизатора и пружинного амортизатора (рис. 10.1, k) для виброизоляции устройства и поглощения энергии удара. Используется когда. juumnjl. м.ф.ф хорошо Рисунок 10.1 I1H§f к и Эластичные элементы делятся на элементы, которые подвержены скручиванию, изгибу и сложной деформации в зависимости от типа деформации.

Максимальная деформация или максимальная нагрузка, которые не должны превышать допуск, обычно устанавливаются в рабочих условиях. Людмила Фирмаль

Для RE с линейными упругими свойствами жесткость k постоянна и равна F / f, p / f или T /

Для параллельных соединений RE общая жесткость упругой системы равна сумме жесткостей компонентов. Когда упругие элементы соединены последовательно, каждый элемент деформируется пропорционально его чувствительности, а общая чувствительность системы равна сумме чувствительности всех упругих элементов в системе. Жесткость и чувствительность характеризуют одинаковые свойства упругого элемента, а именно его способность деформироваться под действием внешней нагрузки.

Влияние на упругие свойства влияет на температуру, вибрацию и другие условия эксплуатации. В частности, ошибки, которые проявляются в измерительном устройстве, вызваны неполными упругими свойствами материала, вызывающими упругие последствия и упругий гистерезис. Постэластичный эффект проявляется в задержке деформации элемента по сравнению с изменением приложенной нагрузки. В упругих свойствах (рис. 10.2, б) это явление отмечено сечениями AB и CO на кривой 7. Эластичный гистерезис проявляется в несоответствии характеристик загружаемых элементов (см. Рис. 10.2, б, кривая 2). Величина гистерезиса Af зависит от напряжения материала элемента.

Поэтому в случае измерительных элементов допустимое напряжение не является прочностными свойствами материала, а связано с допустимым значением гистерезиса, но это значение не превышает 0,5 … 1,5% от значения, т. Е. (A / y / max) — 100 £ 0,5 … 1,5 Постоянство и стабильность упругих свойств элемента достигается за счет правильного выбора материала, режима его термообработки и максимального значения рабочей нагрузки. Материал упругого элемента должен иметь высокие упругие свойства и высокую прочность при переменной нагрузке. Некоторые типы элементов должны быть устойчивы к коррозии и иметь хорошее электрическое и магнитное сопротивление.

Блоки питания и измерительные элементы выполнены из высокоуглеродистых пружин 65G, 60S2,70S2 и инструментальной стали U8, U10, U12. Магнитные и коррозионностойкие пружины для контактов и моментов (см. Рис. 10.1

Источник

Сопротивление материалов. Шпаргалка для студентов

Настоящее издание поможет систематизировать полученные ранее знания, а также подготовиться к экзамену или зачету и успешно их сдать.

Оглавление

Приведённый ознакомительный фрагмент книги Сопротивление материалов. Шпаргалка для студентов предоставлен нашим книжным партнёром — компанией ЛитРес.

6. Механические характеристики свойств материала

Для правильного побора материала при расчетах машин и сооружений надо знать механические свойства подбираемых материалов, к которым относятся:

— прочность — способность материала выдерживать воздействие внешних сил без разрушения и возникновения опасных последствий;

— пластичность — способность материала накапливать пластические деформации до разрушения;

— упругость — способность материала восстанавливать свою форму и размеры после удаления нагрузки;

— жесткость — способность тела противостоять упругой деформации и разрушению при воздействии.

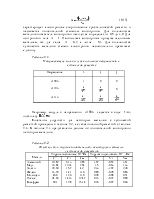
Все детали перед введением в эксплуатацию подвергаются механическим испытаниям, что позволяет определить характеристики свойств материалов. Наиболее распространенным испытанием является растяжение. На начальном этапе растяжения абсолютные деформации пропорциональны нагрузке, а относительные деформации пропорциональны напряжению, т. е. справедлив закон Гука. Пределом пропорциональности σ_пц называется максимальное напряжение, при котором выполняется закон Гука. При достижении нагрузкой некоторой величины в образце появляются остаточные деформации. Пределом упругости σ_0,05 называют максимальное напряжение, при котором не возникают остаточные деформации. Принято считать за максимальное то напряжение, при котором в испытуемом образце появляются деформации 0,05 %. Предел пропорциональности, предел упругости, модуль упругости и коэффициент поперечной деформации характеризуют упругие свойства материала. Предел текучести материала σ_m — это наименьшее напряжение, при котором деформация увеличивается без заметного увеличения нагрузки. Если после возникновения текучести продолжать увеличивать действие нагрузки, наступает разрушение. Пределом прочности (временным сопротивлением) σ_в называют напряжение, соответствующее максимальной нагрузке, предшествующей разрушению образца. Пределы текучести и прочности характеризуют прочность материала. Также существуют две величины, характеризующие пластичность материала: относительное остаточное удлинение δ (отношение изменения длины к начальной длине образца) и относительное остаточное сужение ψ (отношение изменения сечения к первоначальной площади сечения).

Испытания на сжатие для пластичных тел в начале дают результаты, похожие на растяжение, но при нарастании нагрузки пластичные тела не разрушаются, а сплющиваются. Поэтому целесообразнее таким испытаниям подвергать хрупкие тела с малым относительным остаточным удлинением при разрыве. Как правило, в таких испытаниях определяется предел прочности σ с _в — максимальное напряжение, соответствующее максимальной нагрузке.

Источник

iSopromat.ru

Механическими характеристиками материалов называют их упругие свойства, характеризующие способность сопротивляться разрушению (прочность) и деформациям (жёсткость).

Многообразие материалов, используемых при изготовлении элементов конструкций, объясняется тем, что различные материалы имеют неодинаковые свойства, которые используются инженерами для решения тех или иных технологических задач.

В сопромате, исследование механических характеристик необходимо для того чтобы учитывать соответствующие свойства материалов при расчетах на прочность, жесткость и устойчивость.

Например, при расчетах на прочность используются такие характеристики материалов как предел текучести и предел прочности. Они применяются в основном для определения величины допустимых напряжений (расчетного сопротивления) в соответствующих элементах конструкций.

Интервал напряжений, в пределах которого в элементах конструкций имеют место исключительно упругие деформации, ограничивается пределом упругости.

Модули упругости I рода (модуль Юнга) и II рода (модуль сдвига) показывают упругие свойства материалов, и характеризуют их способность сопротивляться продольным и сдвигающим деформациям соответственно.

Коэффициент Пуассона (поперечной деформации) устанавливает зависимость между продольной и поперечной деформациями различных материалов.

Механические характеристики для практически всех материалов определены экспериментально и приведены в соответствующих справочниках.

Основным экспериментом по определению характеристик материалов является испытание на растяжение.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Лекция 2. Упругие и прочностные характеристики материалов

Значение некоторых употребляемых в данной статье понятий и определений приводится отдельно.

Геометрические характеристики рассматриваемого тела, уравнения равновесия и метод сечений позволяют определить значение напряжений в любой точке рассматриваемого сечения. Соответственно суть расчета на прочность сводится к тому, что напряжение σ в наиболее нагруженной точке (на некоторой элементарной площади) должно быть меньше или равно сопротивлению материала:

σ ≤ R (318.1)

Диаграммы напряжений

На сегодняшний день существует несколько методик испытания образцов материалов. При этом одним из самых простых и показательных являются испытания на растяжение (на разрыв), позволяющие определить предел пропорциональности, предел текучести, модуль упругости и другие важные характеристики материала. Так как важнейшей характеристикой напряженного состояния материала является деформация, то определение значения деформации при известных размерах образца и действующих на образец нагрузок позволяет установить вышеуказанные характеристики материала.

Испытания металлов на растяжение проводятся согласно ГОСТ 1497-84. Для этого используются стандартные образцы. Методика испытаний выглядит приблизительно так: к образцу прикладывается статическая нагрузка, определяется абсолютное удлинение образца Δl, затем нагрузка увеличивается на некоторое шаговое значение и снова определяется абсолютное удлинение образца и так далее. На основании полученных данных строится график зависимости удлинений от нагрузки. Этот график называется диаграммой напряжений.

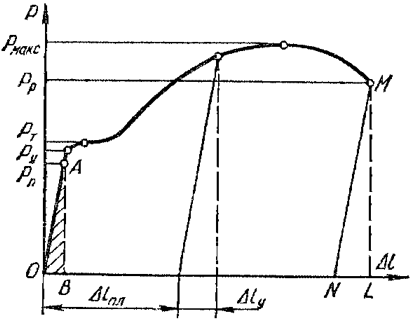
Рисунок 318.1. Диаграмма напряжений для стального образца.

На данной диаграмме мы видим 5 характерных точек:

1. Предел пропорциональности Р_п (точка А)

Нормальные напряжения в поперечном сечении образца при достижении предела пропорциональности будут равны:

Предел пропорциональности ограничивает участок упругих деформаций на диаграмме. На этом участке деформации прямо пропорциональны напряжениям, что выражается законом Гука:

Р_п = kΔl (318.2.2)

k = EF/l (318.2.3)

Модули упругости

Главными характеристиками упругих свойств материалов являются модуль Юнга Е (модуль упругости первого рода, модуль упругости при растяжении), модуль упругости второго рода G (модуль упругости при сдвиге) и коэффициент Пуассона μ (коэффициент поперечной деформации).

Модуль Юнга Е показывает отношение нормальных напряжений к относительным деформациям в пределах пропорциональности

Модуль Юнга также определяется опытным путем при испытании стандарт­ных образцов на растяжение. Так как нормальные напряжения в материале равны силе, деленной на начальную площадь сечения:

σ = Р/F_о (318.3.1), (317.2)

то модуль Юнга согласно закону Гука можно выразить так

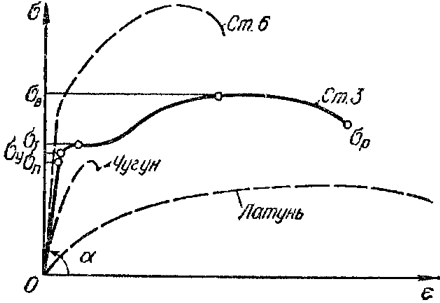
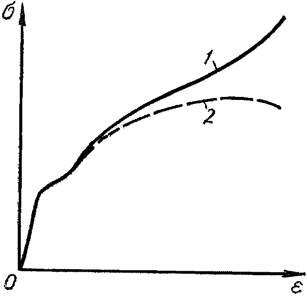
Рисунок 318.2. Диаграммы напряжений некоторых сплавов металлов

Коэффициент Пуассона μ показывает отношение поперечных деформаций к продольным

Под воздействием нагрузок не только увеличивается длина образца, но и уменьшается площадь рассматриваемого поперечного сечения (если предположить, что объем материала в области упругих деформаций остается постоянным, то значит увеличение длины образца приводит к уменьшению площади сечения). Для образца, имеющего круглое сечение, изменение площади сечения можно выразить так:

Тогда коэффициент Пуассона можно выразить следующим уравнением:

Модуль сдвига G показывает отношение касательных напряжений т к углу сдвига

Модуль сдвига G может быть определен опытным путем при испытании образцов на кручение.

т = Р/F (318.3.6)

а тангенс угла наклона можно выразить отношением абсолютной деформации Δl к расстоянию h от места фиксации абсолютной деформации до точки, относительно которой осуществлялся поворот:

tgγ = Δl/h (318.3.7)

то при малых значениях угла сдвига модуль сдвига можно выразить следующим уравнением:

G = т/γ = Ph/FΔl (318.3.8)

Модуль Юнга, модуль сдвига и коэффициент Пуассона связаны между собой следующим отношением:

Е = 2(1 + μ)G (318.3.9)

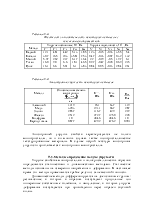
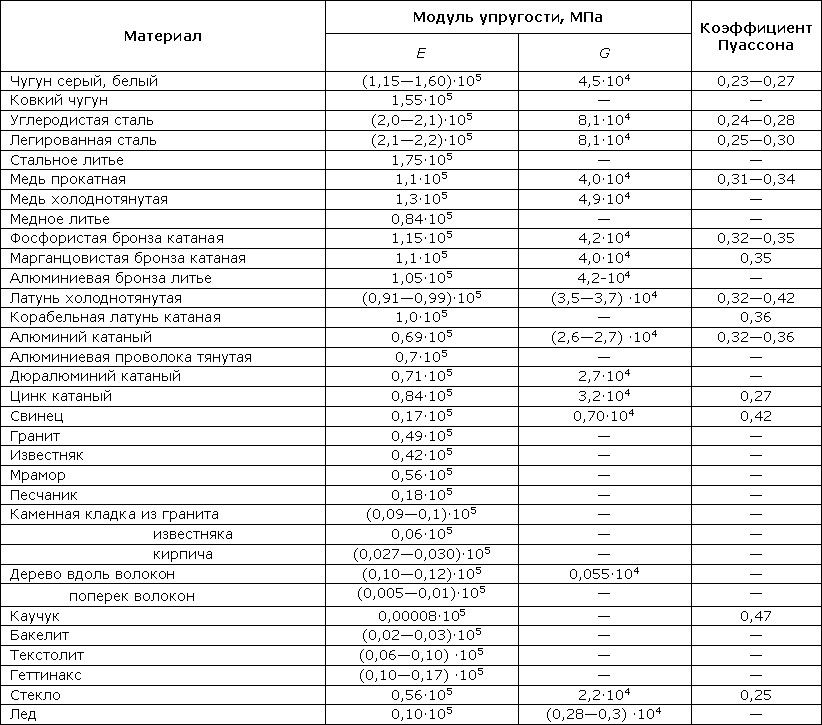
Значения постоянных Е, G и µ приводятся в таблице 318.1

Таблица 318.1. Ориентировочные значения упругих характеристик некоторых материалов

Примечание: Модули упругости являются постоянными величинами, однако технологии изготовления различных строительных материалов меняются и более точные значения модулей упругости следует уточнять по действующим в настоящий момент нормативным документам. Модули упругости бетона зависят от класса бетона и потому здесь не приводятся.

Упругие характеристики определяются для различных материалов в пределах упругих деформаций, ограниченных на диаграмме напряжений точкой А. Между тем на диаграмме напряжений можно выделить еще несколько точек:

2. Предел упругости Р_у

Нормальные напряжения в поперечном сечении образца при достижении предела упругости будут равны:

Предел упругости ограничивает участок на котором появляющиеся пластические деформации находятся в пределах некоторой малой величины, нормированной техническими условиями (например 0,001%; 0,01% и т. д.). Иногда предел упругости обозначается соответственно допуску σ_0.001, σ_0.01 и т.д.

3. Предел текучести Р_т

На диаграммах напряжений отмечен нижний предел текучести. Именно этот предел для большинства материалов принимается за нормативное сопротивление материала.

Некоторые материалы не имеют выраженной площадки текучести. Для них за условный предел текучести σ_0.2 принимается напряжение, при котором остаточное удлинение образца достигает значения ε ≈0,2%.

4. Предел прочности Р_макс (временное сопротивление)

Нормальные напряжения в поперечном сечении образца при достижении предела прочности будут равны:

После преодоления верхнего предела текучести (на диаграммах напряжения не показан) материал снова начинает сопротивляться нагрузкам. При максимальном усилии Р_макс начинается полное разрушение внутренних связей материала. При этом пластические деформации концентрируются в одном месте, образуя в образце так называемую шейку.

Напряжение при максимальной нагрузке называется пределом прочности или временным сопротивлением материала.

Таблица 318.2 Ориентировочные пределы прочности на сжатие (временные сопротивления) некоторых строительных материалов.

Примечание: Для металлов и сплавов значение пределов прочности следует определять согласно нормативных документов. Значение временных сопротивлений для некоторых марок стали можно посмотреть здесь.

Таблица 318.3. Ориентировочные пределы прочности (временные сопротивления) для некоторых пластмасс

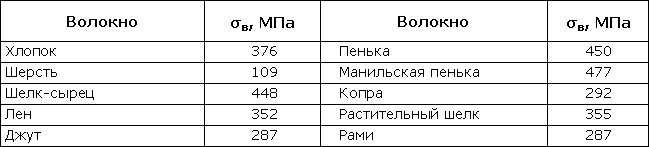
Таблица 318.4. Ориентировочные пределы прочности для некоторых волокон

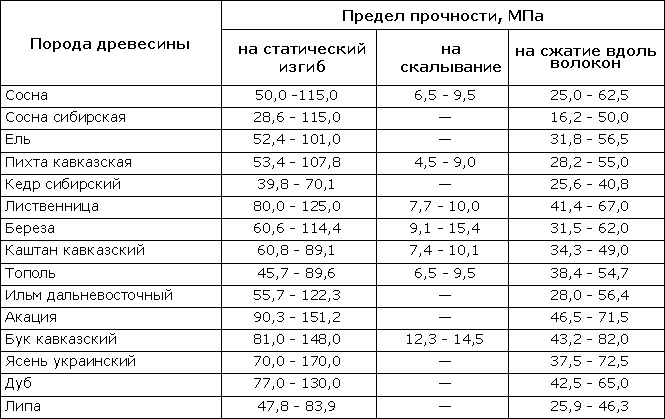
Таблица 318.5. Ориентировочные пределы прочности для некоторых древесных пород

5. Разрушение материала Р_р

Если посмотреть на диаграмму напряжений, то создается впечатление, что разрушение материала наступает при уменьшении нагрузки. Такое впечатление создается потому, что в результате образования «шейки» значительно изменяется площадь сечения образца в районе «шейки». Если построить диаграмму напряжений для образца из малоуглеродистой стали в зависимости от изменяющейся площади сечения, то будет видно, что напряжения в рассматриваемом сечении увеличиваются до некоторого предела:

Тем не менее более правильным является рассмотрение прочностных характеристик материала по отношению к площади первоначального сечения, так как расчетами на прочность изменение первоначальной геометрической формы редко предусматривается.

Одной из механических характеристик металлов является относительное изменение ψ площади поперечного сечения в районе шейки, выражаемое в процентах:

Если сложить разорванные части образца и измерить его удлинение, то выяснится, что оно меньше удлинения на диаграмме (на длину отрезка NL), так как после разрыва упругие деформации исчезают и остаются только пластические. Величина пластической деформации (удлинения) также является важной характеристикой механических свойств материала.

За пределами упругости, вплоть до разрушения, полная деформация состоит из упругой и пластической составляющих. Если довести материал до напряжений, превышающих предел текучести (на рис. 318.1 некоторая точка между пределом текучести и пределом прочности), и затем разгрузить его, то в образце останутся пластические деформации, но при повторном загружении через некоторое время предел упругости станет выше, так как в данном случае изменение геометрической формы образца в результате пластических деформаций становится как бы результатом действия внутренних связей, а изменившаяся геометрическая форма, становится начальной. Этот процесс загрузки и разгрузки материала можно повторять несколько раз, при этом прочностные свойства материала будут увеличиваться:

Рисунок 318.4. Диаграмма напряжений при наклепе (наклонные прямые соответствуют разгрузкам и повторным загружениям)

Такое изменение прочностных свойств материала, получаемое путем повторяющихся статических загружений, называется наклепом. Тем не менее при повышении прочности металла путем наклепа уменьшаются его пластические свойства, а хрупкость увеличивается, поэтому полезным как правило считается относительно небольшой наклеп.

Работа деформации

Прочность материала тем выше, чем больше внутренние силы взаимодействия частиц материала. Поэтому величина сопротивления удлинению, отнесенная к единице объема материала, может служить характеристикой его прочности. В этом случае предел прочности не является исчерпывающей характеристикой прочностных свойств данного материала, так как он характеризует только поперечные сечения. При разрыве разрушаются взаимосвязи по всей площади сечения, а при сдвигах, которые происходят при всякой пластической деформации, разрушаются только местные взаимосвязи. На разрушение этих связей затрачивается определенная работа внутренних сил взаимодействия, которая равна работе внешних сил, затрачиваемой на перемещения:

А = РΔl/2 (318.4.1)

При упругой деформации работа сил определяется площадью треугольника ОАВ (см. рис. 318.1). Полная работа, затраченная на деформацию образца и его разрушение:

А = ηР_максΔl_макс (318.4.2)

Работа, затрачиваемая на пластические деформации и разрушение образца, является одной из важных характеристик материала, определяющих степень его хрупкости.

Деформация сжатия

Деформации сжатия подобны деформациям растяжения: сначала происходят упругие деформации, к которым за пределом упругости добавляются пластические. Характер деформации и разрушения при сжатии показан на рис. 318.5:

Рисунок 318.5

Если материал находится под нагрузкой при постоянном напряжении, то к практически мгновенной упругой деформации постепенно прибавляется добавочная упругая деформация. При полном снятии нагрузки упругая деформация уменьшается пропорционально уменьшающимся напряжениям, а добавочная упругая деформация исчезает медленнее.

Образовавшаяся добавочная упругая деформация при постоянном напряжении, которая исчезает не сразу после разгрузки, называется упругим последействием.

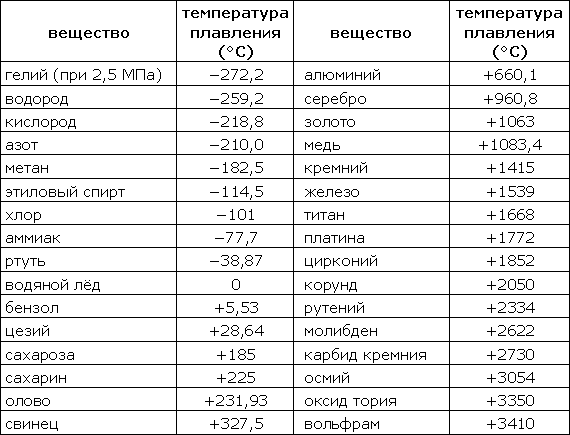
Влияние температуры на изменение механических свойств материалов

Таблица 318.6. Температуры плавления некоторых веществ

Примечание: В таблице приведены температуры плавления при атмосферном давлении (кроме гелия).

Упругие и прочностные характеристики материалов, приведенные в таблицах 318.1-318.5, определяются как правило при температуре +20 о С. ГОСТом 25.503-97 допускается проводить испытания металлических образцов в диапазоне температур от +10 до +35 о С.

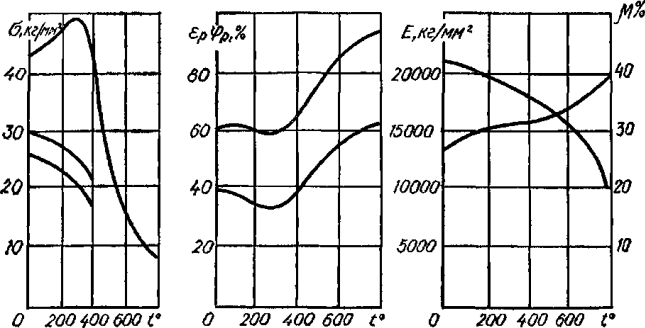
При изменении температуры изменяется потенциальная энергия тела, а значит, изменяется и значение внутренних сил взаимодействия. Поэтому механические свойства материалов зависят не только от абсолютной величины температуры, но и от продолжительности ее действия. Для большинства материалов при нагреве прочностные характеристики (σ_п, σ_т и σ_в) уменьшаются, при этом пластичность материала увеличивается. При снижении температуры прочностные характеристики увеличиваются, но при этом повышается хрупкость. При нагреве уменьшается модуль Юнга Е, а коэффициент Пуассона увеличивается. При снижении температуры происходит обратный процесс.

Рисунок 318.6. Влияние температуры на механические характеристики углеродистой стали.

При нагревании цветных металлов и сплавов из них прочность их сразу падает и при температуре, близкой к 600° С, практически теряется. Исключение составляет алюмотермический хром, предел прочности которого с увеличением температуры увеличивается и при температуре равной 1100° С достигает максимума σ_в1100 = 2σ_в20.

Влияние радиоактивного облучения на изменение механических свойств

Радиоактивное облучение по-разному влияет на различные материалы. Облучение материалов неорганического происхождения по своему влиянию на механические характеристики и характеристики пластичности подобно понижению температуры: с увеличением дозы радиоактивного облучения увеличивается предел прочности и особенно предел текучести, а характеристики пластичности снижаются.

Лекция 3. Методики расчета конструкций.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник