Для чего нужны формулы сокращенного умножения

Для чего нужны формулы сокращенного умножения

Формулы сокращённого умножения (квадрат суммы и разности, куб суммы и разности, разность квадратов, сумма и разность кубов) крайне необходимы во всех разделах математики. Они применяются в упрощении выражений, решении уравнений, умножении многочленов, сокращении дробей, решении интегралов и т.д. и т.п. Короче, есть все основания разобраться с ними. Понять откуда они берутся, зачем они нужны, как их запомнить и как применять.

Откуда берутся формулы сокращённого умножения?

Равенства 6 и 7 записаны не очень привычно. Как бы наоборот. Это специально.) Любое равенство работает как слева направо, так и справа налево. В такой записи понятнее, откуда берутся ФСУ.

Они берутся из умножения.) Например:

(a+b) 2 =(a+b)(a+b)=a 2 +ab+ba+b 2 =a 2 +2ab+b 2

Зачем нужны формулы сокращённого умножения?

С точки зрения математики равенства:

вообще-то, абсолютно равнозначны. Это одно и то же равенство. Но первая запись никаких новых возможностей не даёт. Умножение, и всё тут. А вот вторая запись резко повышает ваш математический уровень. Сомневаетесь? Не надо.) Потому, что равенство:

есть разложение на множители. А это, между прочим, поважнее простого умножения будет, да. ) Кто не в курсе, сходите по ссылке, сами убедитесь. И такое разложение на множители имеет место во всех формулах сокращённого умножения! Если глянуть на список, в левой части каждого равенства мы увидим умножение скобок:

Я даже не поленюсь переписать этот перечень ещё раз, но в другом виде):

Такая запись замечательно подходит для разложения на множители, и, следовательно, для упрощения и решения огромного количества самых разнообразных примеров. Полезная штука. Но есть одна проблемка. Как это всё запомнить?

Как запомнить формулы сокращённого умножения?

Думаю, выражения с названиями сумма кубов и разность кубов вас уже не поставят в тупик.

Сложнее запомнить сами формулы. Здесь как раз тот случай, когда необходима механическая память. Итак, запоминаем квадрат суммы:

Просто пучить глазки на формулу будет недостаточно.) Очень сильно рекомендую надёжно зазубрить (именно зазубрить!) словесную формулировку:

Квадрат суммы равен: квадрат первого числа плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа.

Это заклинание реально помогает решать различные задания школьной математики. Ниже сами увидите. Более того, в ВУЗе, при работе с интегралами, вы эту формулировку не один раз вспомните.

Дальше уже легче. Можно включать логику. Идём по возрастанию трудности. Формула для квадрата разности:

Найдите отличие от квадрата суммы.) Да, перед удвоенным произведением появился минус. Должен же он где-то появиться?! Перед a 2 и b 2 он появиться не может, т.к. любое число в квадрате есть число положительное. Только в серединке.)

Переходим к сумме кубов и разности кубов:

Кстати, сравните выражения во вторых скобках с формулами квадрата суммы/разности.

Ну и последняя парочка. Куб суммы и куб разности:

Как применять формулы сокращённого умножения?

Начнём с прямого применения ФСУ, для разминки.)

Редкий кадр не увидит здесь квадрат скобок!) Конечно, можно и просто перемножить, но нам размяться нужно, правда?) Пишем:

Видим квадрат суммы и вспоминаем заклинание):

«Квадрат первого числа. «. За первое число у нас идёт 3х. Квадрат будет 9х 2 :

Всё. Осталось перемножить то, что перемножается (два на три и пять во втором слагаемом) и получим ответ:

Это была разминка. Теперь задание покруче.)

Разложить на множители:

Во. Смотрим на формулы сокращённого умножения. На второй список, который удобен для разложения на множители. Там нашего выражения нет). Здесь важно вспомнить, что под буквами a и b могут скрываться любые числа, буквы и другие выражения. Поэтому ищем похожую формулу. И зацепкой будут степени переменной!

Но не факт, что квадрат суммы сработает, совсем не факт! Надо убедиться, что наше выражение точно совпадает с левой частью этого равенства. Только тогда можно будет записать и правую часть, т.е. разложение на множители. Проверяем выражение по шагам. Напишу, для удобства, прямо одно под другим:

Всё, можно записывать разложение?

Нужна последняя, окончательная проверка по 12х. Надо убедиться, что 12х точно соответствует 2ab. Вспоминаем заклинание):

«Квадрат суммы равен: квадрат первого числа плюс удвоенное произведение первого числа на второе, плюс квадрат второго числа».

Идея решения понятна? Сначала ищем в списке похожее выражение. Затем сверяем с ним то, что дано в задании на полное соответствие. Если всё совпало, записываем ответ по формуле. Если не совпало (бывает такое), значит раcкладывать наше выражение надо как-то по-другому.

Теперь плавно переместимся в старшие классы. Вы не поверите, но формулы сокращённого умножения там тоже нужны!)

Вся мощь тригонометрии слабо помогает в этом примере. Только седьмой класс и спасает, да. )

Конечно, это выражение похоже на квадрат суммы. Вот и попробуем его применить к этому выражению. Что будет скрываться под буквами а и b? Очевидно, sin 2 x и cos 2 x. Удвоенное произведение, ежу понятно, будет 2sin 2 xcos 2 x, как в нашем выражении и записано. Можно смело применять формулу сокращённого умножения:

А вот теперь и тригонометрия в дело сгодится! Что у нас в скобочках? У нас в скобочках основное тригонометрическое тождество!

Единица в квадрате всё равно единица будет. Вот и ответ:

Конечно, подобные примеры в этом уроке легко решаются. Но на практике, когда человек погружён в синусы и логарифмы, разложение на множители просто не приходит в голову. Проверяйте хитрые примеры на алгебру седьмого класса!

Ещё из той же оперы:

4lg 2 2+4lg2·lg250+lg 2 250 =

Пример хитрый, да. ) Логарифмические формулы как-то трудно применить. Проверим на алгебру? Выражение похоже на квадрат суммы. Тогда что пойдёт за букву а? За букву а пойдёт 2lg2. За букву b пойдёт lg250. Удвоенное произведение будет. будет. 4lg2·lg250. Да! Совпало! Это квадрат суммы. Можно записать:

4lg 2 2+4lg2·lg250+lg 2 250 =(2lg2+lg250) 2

А вот теперь, в скобках, действия с логарифмами хорошо идут!

(2lg2+lg250) 2 =(lg4+lg250) 2 =lg 2 1000=3 2 = 9

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

А вот здесь можно познакомиться с функциями и производными.

Источник

Формулы сокращенного умножения: таблица, примеры использования

Формулы сокращенного умножения (ФСУ) применяются для возведения в степень и умножения чисел и выражений. Часто эти формулы позволяют произвести вычисления более компактно и быстро.

В данной статье мы перечислим основные формулы сокращенного умножения, сгруппируем их в таблицу, рассмотрим примеры использования этих формул, а также остановимся на принципах доказательств формул сокращенного умножения.

Формулы сокращенного умножения. Таблица

Впервые тема ФСУ рассматривается в рамках курса «Алгебра» за 7 класс. Приведем ниже 7 основных формул.

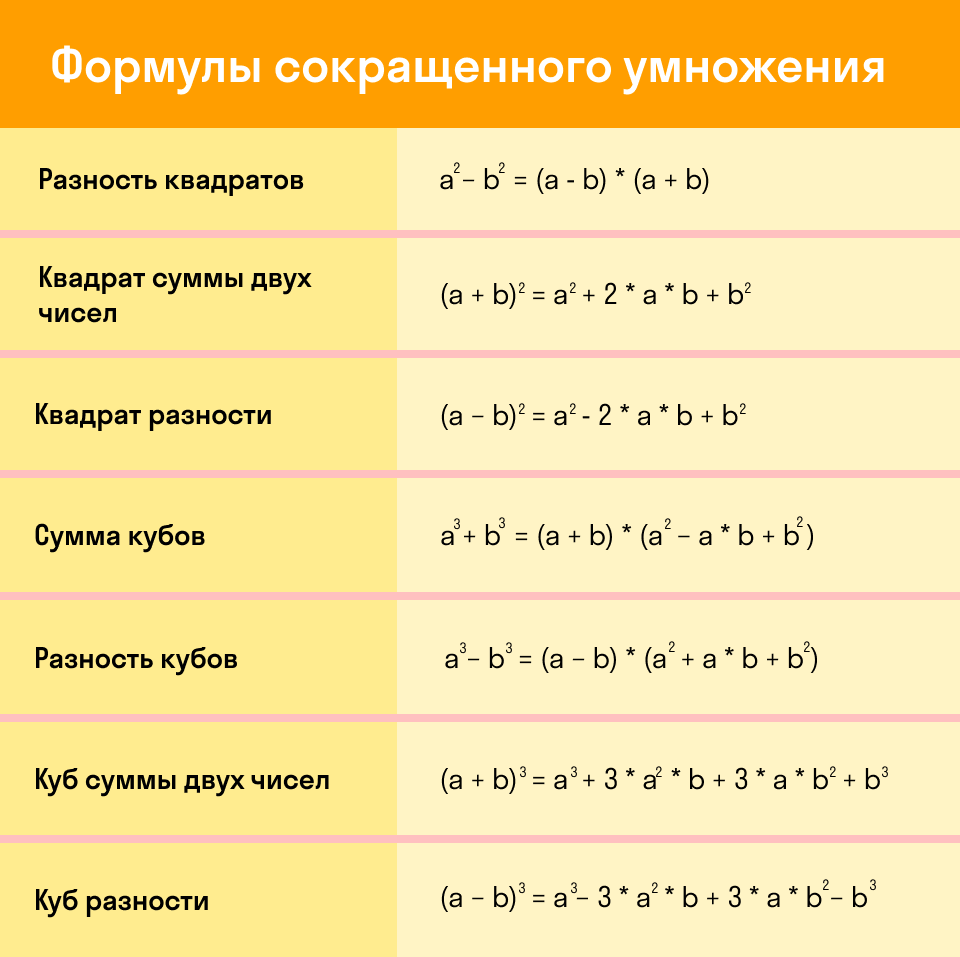
Формулы сокращенного умножения

Буквами a, b, c в данных выражениях могут быть любые числа, переменные или выражения. Для удобства использования лучше выучить семь основных формул наизусть. Сведем их в таблицу и приведем ниже, обведя рамкой.

Первые четыре формулы позволяют вычислять соответственно квадрат или куб суммы или разности двух выражений.

Пятая формула вычисляет разность квадратов выражений путем произведения их суммы и разности.

Формула сокращенного умножения иногда еще называют тождествами сокращенного умножения. В этом нет ничего удивительного, так как каждое равенство представляет собой тождество.

При решении практических примеров часто используют формулы сокращенного умножения с переставленными местами левыми и правыми частями. Это особенно удобно, когда имеет место разложение многочлена на множители.

Дополнительные формулы сокращенного умножения

Не будем ограничиваться курсом 7 класса по алгебре и добавим в нашу таблицу ФСУ еще несколько формул.

Во-первых, рассмотрим формулу бинома Ньютона.

Но что, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два? Полезной будет формула квадрата суммы трех, четырех и более слагаемых.

Как читать эту формулу? Квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Для четных показателей 2m:

Для нечетных показателей 2m+1:

Как читать формулы сокращенного умножения?

Дадим соответствующие формулировки для каждой формулы, но сначала разберемся с принципом чтения формул. Удобнее всего делать это на примере. Возьмем самую первую формулу квадрата суммы двух чисел.

Говорят: квадрат суммы двух выражений a и b равен сумме квадрата первого выражения, удвоенного произведения выражений и квадрата второго выражения.

квадрат разности двух выражений a и b равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражения.

С учетом этого, формулы суммы и разности кубов прочитаются так:

Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.

Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.

Доказательство ФСУ

Доказать ФСУ довольно просто. Основываясь на свойствах умножения, проведем умножение частей формул в скобках.

Для примера рассмотрим формулу квадрата разности.

Чтобы возвести выражение во вторую степень нужно это выражение умножить само на себя.

Формула доказана. Остальные ФСУ доказываются аналогично.

Примеры применения ФСУ

Применим формулу суммы квадратов и получим:

Сокращаем и получаем:

Казалось бы, сложное вычисление проведено быстро всего лишь с использованием формул сокращенного умножения и таблицы умножения.

Источник

Сокращенное умножение: правила, формулы

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Формулы сокращенного умножения

Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть. Да, алгебра такая, нужно быть готовым много запоминать.

Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.

Как читать формулы сокращенного умножения

Учимся проговаривать формулы сокращенного выражения:

Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.

Доказательство формул сокращенного умножения

Остальные ФСУ можно доказать аналогичным методом.

Дополнительные формулы сокращенного умножения

К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.

Бином Ньютона

Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:

Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:

ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.

Формула возведения в квадрат суммы трех, четырех и более слагаемых

Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.

Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.

Формула разности n-ых степеней двух слагаемых

a n − b n = (a − b) * (a n-1 + a n-2 * b + a n-3 * b 2 + … + a * b n-2 + b n-1 ).

Для четных показателей можно записать так:

a 2*m − b 2*m = (a 2 − b 2 ) *(a 2*m−2 + a 2*m−4 * b 2 + a 2*m−6 * b 4 + … + b 2*m−2 ).

Для нечетных показателей:

a 2*m+1 − b 2*·m+1 = (a − b) * (a 2*m + a 2*m−1 * b + a 2*m−2 * b 2 + … + b 2*m ).

Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.

Решение задач

Давайте потренируемся и рассмотрим примеры с дробями.

Задание 1

Как решаем: воспользуемся формулой квадрата суммы: (55 + 10) 2 = 55 2 + 2 * 55 * 10 + 10 2 = 3025 + 1100 + 100 = 4225.

Задание 2

Что сделать: упростить выражение 64 * с 3 – 8.

Как решаем: применим разность кубов: 64 * с 3 – 8 = (4 * с) 3 – 2 3 = (4 * с – 2)((4 * с) 2 + 4 * с * 2 + 2 2 ) = (4 * с – 2)(16 * с 2 + 8 * с + 4).

Задание 3

Как решаем:

Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂

Источник

Формулы сокращенного умножения (ЕГЭ 2022)

Зачем нужны формулы сокращенного умножения?

С их помощью ты сможешь упростить выражение, привести многочлен к стандартному виду (без раскрытия скобок и приведения подобных)

Ты сможешь легко в уме находить квадраты больших чисел и, например, быстро проверить свои расчеты на экзамене.

Иными словами это сильно экономит время при решении самых разных задач!

В общем их стоит выучить. Начнем?

Формулы сокращенного умножения — коротко о главном

Формулы сокращенного умножения – это формулы, зная которые можно избежать выполнения некоторых стандартных действий при упрощении выражений или разложении многочленов на множители.

Формулы сокращенного умножения нужно знать наизусть!

Квадрат суммы

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения:

Название «Формулы сокращенного умножения» совсем не случайно, потому что эти формулы позволяют сократить время на умножение. Вот смотри…

Возьмем самую простую первую формулу квадрата суммы \( <<\left( a+b \right)>^<2>>\) — и попробуем возвести сумму в скобках в квадрат, то есть, умножить \( \left( a+b \right)\) само на себя:

Приведи подобные слагаемые и ты получишь формулу сокращенного умножения квадрат суммы:

Таким образом выводятся все формулы сокращенного умножения.

Ты можешь выводить их каждый раз самостоятельно, а можешь не тратить на это время и быстро посчитать необходимый пример, зная конечное значение формул.

Конечно, квадрат суммы посчитать вручную не так сложно, но что ты скажешь насчет куба суммы или куба разности?

Куб суммы означает, что необходимо \( \left( a+b \right)\) само умножить на себя три раза:

И это мы расписали перемножение только первой скобки, а тоже самое необходимо сделать со второй и с третьей… Согласись, запутаться очень легко, а, как правило, от того, как ты посчитаешь это простое действие, зависит ответ всего примера.

Таким образом, формулы сокращенного умножения позволяют сократить трудоемкое перемножение членов друг на друга и получить быстрый результат.

Как выводится формула для квадрата суммы, мы описали ранее. Попробуем произвести аналогичные действия с квадратом разности.

Квадрат разности

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения:

Квадрат разности означает умножить \( \left( a-b \right)\) само на себя. Попробуй вывести формулу для данного выражения самостоятельно, по аналогии с квадратом суммы.

Справился? Посмотрим, как ты раскрыл скобки:

Что мы делаем дальше? Правильно, приводим подобные слагаемые:

Ты наверняка уже заметил некую закономерность? Присмотрись внимательно к формулам квадрат суммы и квадрат разности. В чем их отличие?

Конечно, ты увидел, что если мы возводим в квадрат разность между \( a\) и \( b\), то мы вычитаем их удвоенное произведение, а если возводим в квадрат сумму, то прибавляем.

При возведении разности и суммы в квадрат, не забывай про удвоенное произведение чисел \( a\) и \( b\)!

Это грубейшая и самая распространенная ошибка!

Попробуй таким способом вычислить следующие выражения:

Ответы:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Посчитай самостоятельно выражения:

Ответы:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Подведем небольшой итог и запишем формулы квадрата суммы и разности в одну строку:

Допустим, у нас есть следующее выражение:

Мы знаем, что квадрат суммы (или разности) – это квадрат одного числа \( +\) квадрат другого числа и \( \pm \) удвоенное произведение этих чисел.

Так как во втором слагаемом есть \( b\), значит, это удвоенное произведение одного и другого числа, соответственно:

\( 24b=2\cdot 3b\cdot x\), где \( \displaystyle x\) – второе число, входящее в нашу скобку.

\( x=\frac<24b><6b>=4\). Второе число, входящее в скобку, равно \( \displaystyle 4\).

Проверим. \( \displaystyle 16\) должно быть равно \( <<4>^<2>>\). Действительно, так и есть, значит, мы нашли оба числа, присутствующие в скобках: \( 4\) и \( 3b\). Осталось определить знак, который стоит между ними. Как ты думаешь, что за знак там будет?

Правильно! Так как мы прибавляем удвоенное произведение, то между числами будет стоять знак сложения. Теперь запиши преобразованное выражение. Справился? У тебя должно получиться следующее:

Заметь: перемена мест слагаемых не сказывается на результате (неважно, сложение или вычитание стоит между \( a\) и \( b\)).

Совершенно необязательно, чтобы слагаемые в преобразуемом выражении стояли так, как написано в формуле.

Посмотри на это выражение: \( 12b+9+4<^<2>>\). Попробуй преобразовать его самостоятельно. Получилось?

Потренируйся – преобразуй следующие выражения:

Ответы:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Справился? Закрепим тему.

Выбери из приведенных ниже выражений те, которые можно представить в виде квадрата суммы или разности.

Ответы:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Разность квадратов

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы:

Еще одна формула сокращенного умножения – разность квадратов.

Разность квадратов — это не квадрат разности!

Разность квадратов двух чисел равна произведению суммы этих чисел на их разность

Проверим, верна ли эта формула. Для этого перемножим \( \left( a-b \right)\left( a+b \right)\), как делали при выведении формул квадрата суммы и разности:

Что мы делаем дальше? Правильно! Приводим подобные слагаемые и получаем:

Таким образом, мы только что удостоверились, что формула действительно верная. Данная формула также упрощает сложные вычислительные действия.

Необходимо вычислить: \( <<145>^<2>>-<<45>^<2>>\). Конечно, мы можем возвести в квадрат \( 145\), затем возвести в квадрат \( 45\) и вычесть одно из другого, но формула упрощает нам задачу:

\( <<145>^<2>>-<<45>^<2>>=\left( 145-45 \right)\cdot \left( 145+45 \right)=100\cdot 190=19000\)

Попробуй самостоятельно посчитать следующие выражения:

Получилось? Сверим результаты:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Так же, как и квадрат суммы (разности), формула разности квадратов может применяться не только с числами:

Умение раскладывать разность квадратов поможет нам преобразовывать сложные математические выражения.

Поскольку \( 3= <<\left( \sqrt<3>\right)>^<2>>\), при разложении на квадрат разности правого выражения мы получим

Будь внимателен и смотри, какое конкретное слагаемое возводится в квадрат!

Для закрепления темы преобразуй следующие выражения:

Записал? Сравним полученные выражения:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Теперь, когда ты усвоил квадрат суммы и квадрат разности, а также разность квадратов, попробуем решать примеры на комбинацию этих трех формул.

Квадрат суммы, квадрат разности, разность квадратов — задачи на комбинацию этих формул

Посмотри внимательно, что ты видишь в числителе? Правильно, числитель — это полный квадрат:

Упрощая выражение, помни, что подсказка, в какую сторону двигаться в упрощении, находится в знаменателе (или в числителе).

В нашем случае, когда знаменатель разложен, и больше ничего сделать нельзя, можно понять, что числителем будет либо квадрат суммы, либо квадрат разности.

Так как мы прибавляем \( 6ab\), то становится ясно, что числитель – квадрат суммы.

Попробуй самостоятельно преобразовать следующие выражения:

А теперь сверь результаты:

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Куб суммы и куб разности

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения:

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения:

Формулы куба суммы и куба разности выводятся аналогичным образом, как квадрат суммы и квадрат разности: раскрытием скобок при перемножении членов друг на друга.

Если квадрат суммы и квадрат разности запомнить весьма легко, то возникает вопрос «как запомнить кубы?»

Посмотри внимательно на две описываемые формулы в сравнении с возведением аналогичных членов в квадрат:

Какую ты видишь закономерность?

Всё перечисленное, кроме зависимости степеней при умножении членов, изображено на рисунке.

Источник