Для чего нужны функции в математике
Что такое функция в математике
Понятие функции в математике появилось не просто так. Давайте разберемся, зачем придумали функцию и как с ней можно работать.
| Сколько времени двигается автомобиль | Сколько км проедет автомобиль |
|---|---|
| 1 час | 60 км |
| 2 часа | 120 км |
| 3 часа | 180 км |
Если внимательно изучить таблицу станет очевидно, что между временем автомобиля в пути и пройденным расстоянием есть четкая зависимость.
Обозначим за « x » время автомобиля в пути.
Обозначим за « y » расстояние, пройденное автомобилем.
Запишем зависимость « y » (расстояния) от « x » (времени в пути автомобиля).
Давайте убедимся, что мы правильно записали зависимость пройденного расстояния от времени в пути.
Теперь вместо « y » запишем обозначение « y(x) ». Такая запись означает, что « y » зависит от « x ».
Окончательная запись нашей функции, которая показывает зависимость пройденного автомобилем расстояния от времени в пути, выглядит следующим образом:
Функцией называют зависимость « y » от « x ».
Запись функции в виде « y(x) = 60x » называют формульным способом задания функции.
Конечно, нужно понимать, что функция « y(x) = 60x » — это не единственная в мире функция. В математике бесконечное множество самых разнообразных функций.
Примеры других функций:
Единственное, что объединяет все функции, это то, что они показывают зависимость значения функция (« y ») от её аргумента (« x »).
Способы задания функции
Задание функции формулой
Через формульный способ задания функции всегда можно сразу по конкретному значению аргумента « x » найти значение функции « y ».
Например, рассмотрим функцию, заданную формульным способом.
Запишем расчет следующим образом.
Табличный способ задания функции
С табличным способом задания функции мы уже встречались, когда расписывали таблицу для функции, которая описывает движение автомобиля « y(x) = 60x ».
Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений « y » для произвольно выбранных значений « x ».
Будьте внимательны, когда подставляете значение « x » в функцию,
у которой перед « x » есть минус.
Нельзя терять знак минуса, который стоит перед « x ».
При подстановки отрицательного числа в функцию вместо « x » обязательно заключайте отрицательное число в скобки. Не забывайте использовать правило знаков.
Подставим в функцию « y(x) = −x + 4 » вместо « x » отрицательное число « −1 ».
Неправильно
Правильно
Запишем полученные результаты в таблицу. Таким образом мы получили табличный способ задания функции « y(x) = −x + 4 ».
| x | y |
|---|---|
| −1 | 5 |
| 0 | 4 |
| 1 | 3 |
Графический способ задания функции
Теперь давайте разберемся, что называют графиком функции и как его построить.
Прежде чем перейти к изучению графического способа задания функции обязательно вспомните, что называют прямоугольной системой координат.
Рассмотрим функцию « y(x) = −2x + 1 ».
Результаты запишем в таблицу.
| x | Расчет |
|---|---|
| −1 | y(−1) = −2 · (−1) + 1 = 2 + 1 = 3 |
| 0 | y(0) = −2 · 0 + 1 = 0 + 1 = 1 |
| 1 | y(1) = −2 · 1 + 1 = −2 + 1 = −1 |
Назовем каждую полученную точку и запишем их координаты в новую таблицу.
| Имя точки | x | y |
|---|---|---|
| (·) A | −1 | 3 |
| (·) B | 0 | 1 |
| (·) C | 1 | −1 |
Соединим отмеченные точки прямой. Проведенная прямая будет графиком функции « y(x) = −2x + 1 ».
График функции — это объединение всех точек, координаты которых мы можем найти, подставляя в функцию произвольные числовые значения вместо « x ».
Другими словами можно сказать, что под графиком функции мы понимаем множество всех точек, координаты которых мы можем найти, подставляя в функцию любые числовые значения вместо « x ».
Полученный график функции « y(x) = −2x + 1 » это бесконечное множество точек, которые лежат на одной прямой.
При многократном увеличении графика функции мы увидим, что в самом деле вся прямая состоит из рядом стоящих точек.
Точки располагаются максимально близко к друг другу, поэтому по расчетам получается, что графиком функции будет являться прямая.
Зачем нужна функция
Для того чтобы понять необходимость существования функции, рассмотрите пример. Любая физическая формула выражает зависимость одного параметра от другого. Так, связь между давлением газа и его температурой при постоянном объеме выражается формулой: р = VТ, т.е. давление р находится в прямой зависимости от температуры Т и является ее линейной функцией.
При написании у = f(х) имеется ввиду некоторая идея зависимости, т.е. переменная у зависит от переменной х по определенному закону или правилу. Этот закон обозначается в функции как f. При этом переменная у может зависеть как от одной, так и от нескольких величин. Например, давление покоящейся жидкости р = ρgh зависит от плотности жидкости ρ, высоты столба жидкости h и от величины ускорения свободного падения g.
Обратите внимание, что посредством применения функции для каждого допустимого значения х получается однозначное значение у. Иными словами, понятие функции выражает идею действия, которое необходимо совершить над одной величиной, чтобы получить другую. В связи с этим в технических дисциплинах функция определяется как устройство, на входе которого подается х, а на выходе возникает у.
Итак, функция позволяет установить соответствие между двумя множествами таким образом, что каждому элементу первого множества соответствует единственный элемент второго множества. При этом данное соответствие выражается определенным правилом или законом.
Функции в математике могут быть выражены различными способами. Наиболее привычным является представление функции в виде формулы: у=sinх, у=2х+3 и т.д. Но существует также наглядный способ выражения функции – в виде графика, например, зависимость инфляции от денежной массы. Некоторые функции представлены в виде таблицы. Этот способ является единственно возможным в том случае, если зависимость устанавливается экспериментально, при этом формула еще не выведена, а график не построен.
Что такое функция?
7 класс, 11 класс, ЕГЭ/ОГЭ
Понятие функции
Определение функции можно сформулировать по-разному. Рассмотрим несколько вариантов, чтобы усвоить наверняка.
1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f.
Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у.
2. Функция — это определенное действие над переменной.
Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у.
В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так:
В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях.
3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике.
Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида
область определения выглядит так:
И записать это можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x2 — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Для примера рассмотрим соответствие между двумя множествами — человек-владелец странички в инстаграм и сама страничка, у которой есть владелец. Такое соответствие можно назвать взаимно-однозначным — у человека есть страничка, и это можно проверить. И наоборот — по аккаунту в инстаграм можно проверить, кто им владеет.
В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция у = 3х +2. Каждому значению х соответствует одно и только одно значение у. И наоборот — зная у, можно сразу найти х.
Что такое функция
Понятие функции – одно из основных в математике.
На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.
Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.
1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.
Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.
2. Можно дать и другое определение.
Функция – это определенное действие над переменной.
Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.
3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.
Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.
Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.
Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:
Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.
А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:
Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.
Очень сложно было бы описать такое соответствие математически, не правда ли?
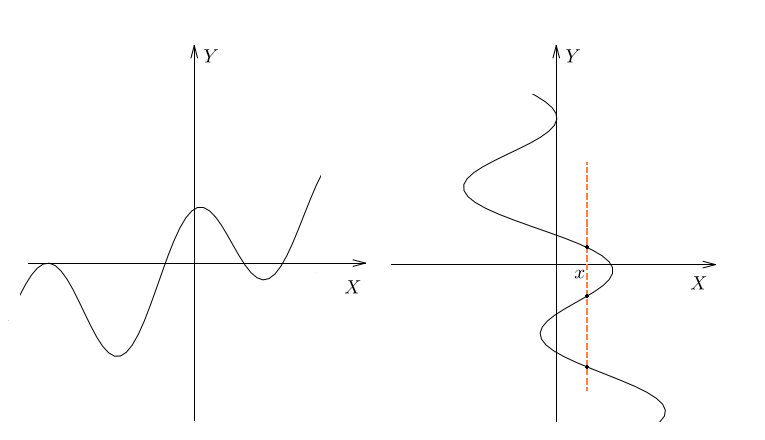
Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?
Ты нашел то, что искал? Поделись с друзьями!
Перечислим способы задания функции.
Это примеры функций, заданных формулами.
К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.
Математические функции в жизни
Описание презентации по отдельным слайдам:
Учебный проект «Применение математических функций в жизни человека и различных науках» Автор проекта: Преподаватель математики Вербицкая Е.В. Энгельс 2015
Возможно ли: определить траекторию полёта космических тел? построить график пословицы «Кашу маслом не испортишь»? задать функцию потребительского спроса?
Цель: выявить и изучить области, в которых применяется функция и её свойства. Задачи: подобрать и проанализировать соответствующую литературу; найти определение функции в школьной программе; Рассмотреть применение функции в точных и естественных науках; Рассмотреть применение функции в истории и филологии; Показать применение функции в жизни человека. Гипотеза: функциональные зависимости существуют во всех сферах жизни человека.
История развития понятия функции с древнейших времён до 17 века
Франсуа Виет (1540 – 1603гг.) История развития понятия функции в 17 веке Рене Декарт (1596-1650гг.) Пьер Ферма (1602-1665гг.)
Применение функций в точных науках Графики зависимости физических величин, Звёздный график, Отображение звуковых волн с помощью периодической функции. С помощью гиперболических функций описывается прогиб каната, зона слышимости звука пролетающего самолета
Линейная функция График равномерного прямолинейного движения. Физика. Зависимость силы тока y=kx+b, графиком является прямая.
Квадратичная функция График равноускоренного прямолинейного движения Физика. Потенциальная энергия.
Линза; Увеличительное стекло; Отражательный телескоп; Прожектор или фара автомобиля Оптика.
Фазы звуковой волны. Звук, колебания за просторами Земли.
Применение функции в естественных науках
Функциональные зависимости в химии
Биология. График функции: «Развитие организма
Применение функций в биологии и химии. Потомство комнатных мух за лето только от одной самки может составить 8 • 1014.
Применение функции в истории и филологии
Пример изображения исторических закономерностей. «График информационного бума»
Графики пословиц «Каши маслом не испортишь» «Пересев хуже недосева»
«Чем дальше в лес, тем больше дров» «Горяч на почине, да скоро остыл»
«Каково проживёшь, такую славу наживёшь» расстояние до кумы м е р а г р е х а «Дальше кумы – меньше греха»
Применение функции в повседневной жизни человека
Функция потребительского спроса B
Применение линейной функции Взлёт ракеты Дверной замок
Применение квадратичной функции Вращающийся сосуд с жидкостью Падения мяча Траектории струй воды Солнечная электростанция
График таяния льда
Функция является неотъемлемой частью нашей жизни и наук в целом, так как функциональные зависимости, действительно, существуют во всех сферах жизни человека.
благодарим за внимание!
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Номер материала: ДБ-112885
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Во всех педвузах страны появятся технопарки
Время чтения: 1 минута
Время чтения: 1 минута
Все школы РФ с 2023 года подключат к государственной информационной системе «Моя школа»
Время чтения: 1 минута
Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.