Для чего нужны круги эйлера
Менее 30 дней
осталось до конца вашей подписки
Продлите подписку сейчас и не пропустите ни одной самой важной книги, способной изменить вас и ваш бизнес!
Получить в подарок обзор книги «Законы влияния» Сьюзан Вайншенк.
Получите бесплатно обзор этой книги на свой email прямо сейчас.
Оставьте свой email и вы сможете скачать «Алгоритм написания текстов»
Спасибо!
Мы будем отправлять вам только интересные и полезные новости!
Спасибо!
Обновите страницу, чтобы статья открылась для чтения.
Спасибо!
Файл доступен вам по ссылке.
Apple
для вас идеален формат epub. Абсолютно все устройства Apple автоматически его распознают и открывают через стандартное приложение iBooks.
Android
Файлы откроются в этих приложениях, они всегда будут в вашем доступе. Вы сможете настроить визуально текст для своего комфорта.
Если вам привычно читать формат pdf и возникают проблемы, то мы подскажем, как их решить.
Windows
Файлы откроются в приложении, будут всегда у вас под рукой, вы также сможете настроить шрифт и яркость.
Если вы предпочитаете читать с экрана компьютера или в распечатанном виде, то рекомендуем скачивать формат pdf.
Для электронных книг мы советуем формат epub или pdf. Вам необходимо будет скачать файлы сначала на Пк, а затем перенести их в память электронной книги через карту памяти или шнур USB.
Спасибо!
Письмо с обзором придет на Вашу почту в течение 10 минут. Проверьте папку «Спам» или «Нежелательная почта».
Спасибо!
Вы скачали уже три обзора книг. Для вас доступ к дальнейшему скачиванию закрыт. Вы сможете читать обзоры, только оформив подписку.
Спасибо!
В течение пары минут вы получите на свой e-mail письмо с бесплатным обзором.
Спасибо!
Мы отправили вам 3 бесплатных обзора на указанный e-mail. Внимательно проверьте папку «Спам» или «Нежелательные» вашего почтового ящика. Если там все же нет письма с книгами – то пишите нам на kratko@knigikratko.ru – мы оперативно вам их пришлем!
Заказ подписки
Оставьте ваши данные для оформления подписки.
Заказ подписки
Круги Эйлера
Подарок для Вас!
Мы пришлем Вам обзор полезной книги.
Идеальный руководитель Ицхак Адизес
Круги Эйлера представляют собой особую геометрическую схему, необходимую для поиска и более наглядного отображения логических связей между понятиями и явлениями, а также для изображения отношений между определенным множеством и его частью. Благодаря наглядности они значительно упрощают любые рассуждения и помогают быстрее находить ответы на вопросы.
Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. С момента своего появления метод приобрел широкую популярность и признание.
Позже круги Эйлера использовали в своих работах многие известные ученые, к примеру, чешский математик Бернард Больцано, немецкий математик Эрнест Шредер, английский философ и логик Джон Венн и другие. Сегодня методика служит основной многих упражнений на развитие мышления, в том числе и упражнений из нашей бесплатной онлайн-программы «Нейробика».
Для чего нужны круги Эйлера
Круги Эйлера имеют прикладное значение, ведь с их помощью можно решать множество практических задач на пересечение или объединение множеств в логике, математике, менеджменте, информатике, статистике и т.д. Полезны они и в жизни, т.к., работая с ними, можно получать ответы на многие важные вопросы, находить массу логических взаимосвязей.
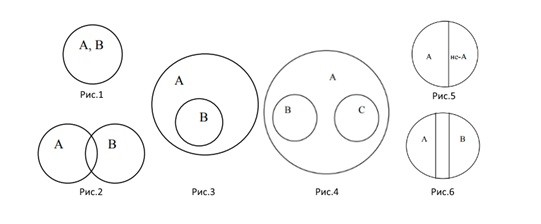
Есть несколько групп кругов Эйлера:
Но в упражнениях на развитие мышления чаще всего встречаются два вида кругов:
Результат использования кругов Эйлера проследить на этом примере очень просто: обдумывая, какую профессию выбрать, вы можете либо долго рассуждать, пытаясь понять, что больше подойдет, а можете нарисовать аналогичную диаграмму, ответить на вопросы и сделать логический вывод.
Применять метод очень просто. Также его можно назвать универсальным – подходящим для людей всех возрастов: от детей дошкольного возраста (в детских садах детям преподают круги, начиная с 4-5-летнего возраста) до студентов (задачи с кругами есть, к примеру, в тестах ЕГЭ по информатике) и ученых (круги широко применяются в академической среде).
Типичный пример кругов Эйлера
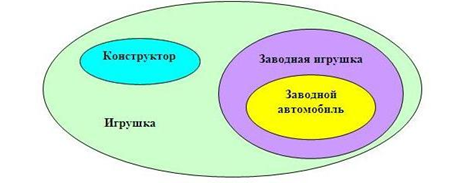
Чтобы вы могли лучше понять, как «работают» круги Эйлера, рекомендуем познакомиться с типичным примером. Обратите внимание на нижеследующий рисунок:
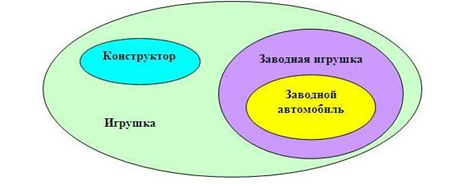
На рисунке зеленым цветов отмечено наибольшее множество, представляющее собой все варианты игрушек. Один из них – это конструкторы (голубой овал). Конструкторы – это отдельное множество само по себе, но в то же время и часть общего множества игрушек.
Заводные игрушки (фиолетовый овал) тоже относятся к множеству игрушек, однако к множеству конструктора они отношения не имеют. Зато заводной автомобиль (желтый овал), пусть и является самостоятельным явлением, но считается одним из подмножеств заводных игрушек.
По подобной схеме строятся и решаются многие задачи (включая и задания на развитие когнитивных способностей), задействующие круги Эйлера. Давайте разберем одну такую задачу (кстати, именно ее в 2011 году внесли на демонстрационный тест ЕГЭ по информатике и ИКТ).
Пример решения задачи с помощью кругов Эйлера
Условия задачи таковы: приведенная таблица показывает, сколько страниц было найдено в Интернете по конкретным запросам:
| Запрос | Найдено страниц (в тысячах) |
| Крейсер/линкор | 7 000 |
| Крейсер | 4 800 |
| Линкор | 4 500 |
Вопрос задачи: сколько страниц (в тысячах) выдаст поисковик по запросу «Крейсер и линкор»? При этом нужно учитывать, что все запросы выполняются примерно в одно и то же время, поэтому набор страниц с искомыми словами со времени выполнения запросов остался неизменным.
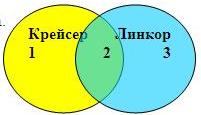
Решается задача так: с помощью кругов Эйлера изображаются условия задачи, а цифрами «1», «2» и «3» обозначаются полученные в результате сегменты:
Учитывая условия задачи, составляем уравнения:
Чтобы определить количество запросов «Крейсер и линкор» (сегмент обозначен цифрой «2» на рисунке), подставим в уравнение 1 уравнение 2 и получим:
4 800 + 3 = 7 000, а значит, что 3 = 2 200 (т.к. 7 000-4 800 = 2 200).
Далее полученный результат подставляем в уравнение 3 и получаем:
2 + 2 200 = 4 500, а это означает, что 2 = 2 300 (т.к. 4 500-2 200 = 2 300).
Ответ: по запросу «Крейсер и линкор» будет найдено 2 300 страниц.
Этот пример наглядно демонстрирует, что с помощью кругов Эйлера можно достаточно быстро и просто решать сложные задачи.
Резюме
Круги Эйлера – это очень полезная методика решения задач и установления логических связей, а заодно и занимательный и интересный способ провести время и потренировать мозг. Так что, если вам хочется совместить приятное с полезным и поработать головой, предлагаем пройти наш курс «Нейробика», включающий в себя самые разные задания, в том числе и круги Эйлера, эффективность которых научно обоснована и подтверждена многолетней практикой.
В нашей Библиотеке вы можете прочитать обзор по книге Тима Кларка, Александра Остервальдера, Ива Пинье «Твоя бизнес-модель. Системный подход к построению карьеры». Авторы книги предлагают интересное решение: подойти к собственной личности как к проекту и разработать бизнес-модель своей карьеры.
Круги Эйлера: как решить задачу с помощью них?
Практикующий психолог, гештальт-терапевт. Закончила Тольяттинский Государ.
Наверняка ты задаешься вопросом: «Геометрия в психологии? Круги Эйлера? Как такое возможно?».
Возможно! Но обо всем по порядку.
Круги Эйлера (на самом деле, может быть любая другая фигура, просто круг – более понятная) были изобретены Леонардом Эйлером, для решения задач. Суть кругов была в том, чтобы показывать отношения между множествами и подмножествами в математике, для наглядного и логического представления. Эйлер считал, что с помощью наглядного изображения можно облегчить размышления человека в решении задач.
Науки всегда связаны, ни одна наука не обходится без математики, а тем более психологи– наука с расчетами и методиками, техниками, самое главное–связанная с организмом и мозгом человека. Исходя из этого, можно сказать, что круги Эйлера можно и нужно использовать для наглядной картинки того, что хочет человек и что с ним происходит в моменте «здесь и сейчас»,, формировать логическое мышление.
Как применить круги Эйлера в психологии
Ты же смотрела «Зачарованных»? Если нет, то наверняка помнишь, что своеобразным логотипом сериала был трилистник заключённый в круг. И это тоже можно отнести к кругам Эйлера, потому что сёстры три- каждый лепесток символизирует отдельную личность, но внутри этой формы образовывается единая фигура и она говорит о том, что в любом случае сёстры связаны между собой.
Круг, в который заключён трилистник означает то, что объединяет сестёр ещё сильнее–это общее дело. Это был наглядный пример, что бы ты представила, каким образом может простая геометрическая фигура заключить в себе целую логическую цепочку, которая будет очень понятна.
В психологии круги Эйлера применяют для того, чтобы человек смог разобраться в самых разных уголках своей жизни. Эта схема помогает в решении дел, так как сразу становится понятно, что для тебя является важным, какого результата ты ждёшь, а также помогает в отношениях между людьми, тут опять играет роль приоритетность и конкретика конечного исхода.
Схемы Эйлера уникальны, но в тоже время очень универсальны, поскольку помогают детям размышлять и логично мыслить, помогают взрослым распутать клубки и рационализировать свои действия.
Принцип кругов Эйлера
Помни про эмблему из «Зачарованных», она тебе понадобится для визуализации.
Круги Эйлера в реальной жизни
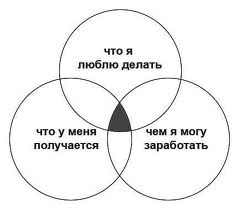
На самом деле, все гениальное просто и самая лучшая и простая техника с техникой Эйлера называется «три круга». Для использования этой несложной техники тебе понадобится три карандаша разного цвета и листок бумаги. Ловкость ума и никакого мошенничества, честно слово! Сейчас ты научишься мыслить ещё более рационально, чем до этого момента!
Помни, что один круг–один инструмент. Например: «что я люблю делать?», «что у меня получается лучше всего?», «как из этого извлечь выгоду или заработок?».
Тут нам и понадобится эмблема из нашумевшего сериала. Нарисуй три круга (у каждого круга свой цвет), так, чтобы круги пересекались образовывая внутри трилистник.
Название круга – это инструмент, присвой каждому кругу свой. Раскрой полностью смысл каждого инструмента. Что-то нравится? Напиши почему нравится. Напиши о том, сколько ты хочешь зарабатывать, укажи причину – поставь себе цель. Напиши, почему у тебя получается делать что-то лучше, чем остальные, похвали себя.
Очень важно рисовать круги до тех пор, пока не образуется этот трилистник. Да, круги могут не пересекаться, тогда нужно думать, как сделать так, чтобы пересеклись, может быть, придётся заменять инструменты. Круги могут быть разного размера, фигура внутри не обязательно должна иметь равные части, самое главное, чтобы эти части были.
Теперь, когда ты нарисовала круги, распределила задачи, в самом центре появилась фигура похожая на треугольник–эта фигура является главным отношением между твоими «подмножествами», она даёт конечный результат. Получившиеся листки – это путь к конечному результату.
Техника «капля в луже»
Эта техника подходит для тебя, если ты не можешь определить свои качества.

Для этого нужно представить себя каплей, которая, попадая в воду даёт множество кругов.
Обозначь себя главным кругом. Далее подобно капле в луже рисуй круги вокруг себя, делая их все больше и больше. Нарисуй минимум пять кругов и обозначь их своими качествами, прислушиваясь к себе. Самый первый круг определяет тебя, последующие же помогают идти по жизни.
Рисуя такие круги, ты находишь в себе те качества, о которых даже не подозревала, они помогут раскрыть твоё потенциал. Если вдруг тебе не нравится какое-то качество в себе, ты можешь проработать этот момент и избавиться от того, что тебе не нравится. Главная задача техники–это понять, какие качества в тебе вообще есть.
Возражаешь? Проработай!
Есть возражения по поводу составления кругов? Проработай их!
Само по себе ничего не пройдёт. Не пускай жизнь на самотёк. Лучше посмотреть на картину мира в кружках сейчас, принять себя такой, какая ты есть и работать с этим, чем на закате жизни жалеть о том, что прожила жизнь неправильно, потому что осознание придёт в любом случае, но комфорт можешь сотворить только ты!
Если ты задумалась о том, что тебе «жалко», то вот прямо сейчас рисуй круги, проговаривай плюсы и минусы работы. Во-первых, если ты ценный сотрудник, то тебе могут платить больше! Ищи инструменты для повышения с помощью схемы Эйлера, примеряй все техники.
Плохой человек никогда не признается в том, что он плохой. Техника «капля в луже» очень тебе подойдёт сразиться с неуверенностью и найти хорошие качества. Они у тебя точно есть!
Эйлер был неглупым человеком. Он доказал всему миру, как просто решать задачи наглядно изображая их в геометрических фигурах. Логическое мышление есть у каждого, а схема Эйлера поможет тебе его разработать. Поэтому обязательно пробуй!
Что даёт построение кругов
Когда ты начнёшь использовать схему в деле, применяя техники и возьмёшь это за правило, твоё мышление натренируется, и ты станешь понимать этот мир лучше, найдёшь своё предназначение.

Разовьётся логическое мышление, ты станешь продуктивнее и рациональнее мыслить.
Да, пересечение «трёх кругов» порой даёт отрицательный результат, ты можешь даже по началу расстроиться от того, что тебя это не устроит. Но тебе нужно понимать, что не все тебе по силам, нет на свете совершенных людей, которые могут по щелчку пальца сделать так, как надо им. У тебя попросту может быть другая цель, которую ты не ощущаешь, потому что она находится глубоко в подсознании. Круги Эйлера как раз и предназначены для того, чтобы найти себя с помощью логики и размышлений, которые распространяются на все аспекты жизни.
Техники универсальны, они подойдут абсолютно для всех аспектов жизни: от бытовых мелочей до глобальных целей в жизни. Просто меняй инструменты, применяя техники и жизнь будет становится проще. Главное – это тренировки. Удачи в поиске себя!
Круги Эйлера
Круги Эйлера представляют собой особую геометрическую схему, необходимую для поиска и более наглядного отображения логических связей между понятиями и явлениями, а также для изображения отношений между определенным множеством и его частью. Благодаря наглядности они значительно упрощают любые рассуждения и помогают быстрее находить ответы на вопросы.
Автором кругов является известный математик Леонард Эйлер, который считал, что они необходимы, чтобы облегчить размышления человека. С момента своего появления метод приобрел широкую популярность и признание.
Позже круги Эйлера использовали в своих работах многие известные ученые, к примеру, чешский математик Бернард Больцано, немецкий математик Эрнест Шредер, английский философ и логик Джон Венн и другие. Сегодня методика служит основной многих упражнений на развитие мышления, в том числе и упражнений из нашей бесплатной онлайн-программы «Нейробика».
Для чего нужны круги Эйлера
Круги Эйлера имеют прикладное значение, ведь с их помощью можно решать множество практических задач на пересечение или объединение множеств в логике, математике, менеджменте, информатике, статистике и т.д. Полезны они и в жизни, т.к., работая с ними, можно получать ответы на многие важные вопросы, находить массу логических взаимосвязей.
Есть несколько групп кругов Эйлера:
Но в упражнениях на развитие мышления чаще всего встречаются два вида кругов:
Результат использования кругов Эйлера проследить на этом примере очень просто: обдумывая, какую профессию выбрать, вы можете либо долго рассуждать, пытаясь понять, что больше подойдет, а можете нарисовать аналогичную диаграмму, ответить на вопросы и сделать логический вывод.
Применять метод очень просто. Также его можно назвать универсальным – подходящим для людей всех возрастов: от детей дошкольного возраста (в детских садах детям преподают круги, начиная с 4-5-летнего возраста) до студентов (задачи с кругами есть, к примеру, в тестах ЕГЭ по информатике) и ученых (круги широко применяются в академической среде).
Типичный пример кругов Эйлера
Чтобы вы могли лучше понять, как «работают» круги Эйлера, рекомендуем познакомиться с типичным примером. Обратите внимание на нижеследующий рисунок:
На рисунке зеленым цветов отмечено наибольшее множество, представляющее собой все варианты игрушек. Один из них – это конструкторы (голубой овал). Конструкторы – это отдельное множество само по себе, но в то же время и часть общего множества игрушек.
Заводные игрушки (фиолетовый овал) тоже относятся к множеству игрушек, однако к множеству конструктора они отношения не имеют. Зато заводной автомобиль (желтый овал), пусть и является самостоятельным явлением, но считается одним из подмножеств заводных игрушек.
По подобной схеме строятся и решаются многие задачи (включая и задания на развитие когнитивных способностей), задействующие круги Эйлера. Давайте разберем одну такую задачу (кстати, именно ее в 2011 году внесли на демонстрационный тест ЕГЭ по информатике и ИКТ).
Пример решения задачи с помощью кругов Эйлера
Условия задачи таковы: приведенная таблица показывает, сколько страниц было найдено в Интернете по конкретным запросам:
| Запрос | Найдено страниц (в тысячах) |
| Крейсер/линкор | 7 000 |
| Крейсер | 4 800 |
| Линкор | 4 500 |
Вопрос задачи: сколько страниц (в тысячах) выдаст поисковик по запросу «Крейсер и линкор»? При этом нужно учитывать, что все запросы выполняются примерно в одно и то же время, поэтому набор страниц с искомыми словами со времени выполнения запросов остался неизменным.
Решается задача так: с помощью кругов Эйлера изображаются условия задачи, а цифрами «1», «2» и «3» обозначаются полученные в результате сегменты:
Учитывая условия задачи, составляем уравнения:
Чтобы определить количество запросов «Крейсер и линкор» (сегмент обозначен цифрой «2» на рисунке), подставим в уравнение 1 уравнение 2 и получим:
4 800 + 3 = 7 000, а значит, что 3 = 2 200 (т.к. 7 000-4 800 = 2 200).
Далее полученный результат подставляем в уравнение 3 и получаем:
2 + 2 200 = 4 500, а это означает, что 2 = 2 300 (т.к. 4 500-2 200 = 2 300).
Ответ: по запросу «Крейсер и линкор» будет найдено 2 300 страниц.
Этот пример наглядно демонстрирует, что с помощью кругов Эйлера можно достаточно быстро и просто решать сложные задачи.
Резюме
Круги Эйлера – это очень полезная методика решения задач и установления логических связей, а заодно и занимательный и интересный способ провести время и потренировать мозг. Так что, если вам хочется совместить приятное с полезным и поработать головой, предлагаем пройти наш курс «Нейробика», включающий в себя самые разные задания, в том числе и круги Эйлера, эффективность которых научно обоснована и подтверждена многолетней практикой.
Круги Эйлера и примеры задач на логику
Круги Эйлера, на самом деле, достаточно часто встречаются в нашей жизни. Еще в младшей школе ученики начинают работать со схематическими фигурами, которые наглядно объясняют соотношения предметов и понятий.
Описание схемы кругов Эйлера
Круги Эйлера – геометрические конструкции, применяемые для упрощения восприятия логических связей между предметами, понятиями и явлениями.
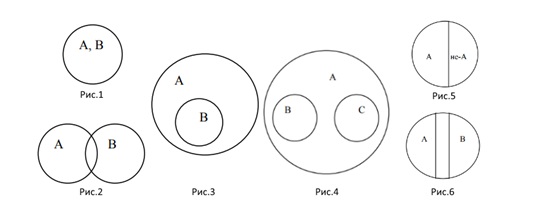
Делятся на группы, в зависимости от типа отношений между множествами:
Типовой пример такой диаграммы:
Наибольшее множество, отмеченное зеленым цветом, представляет собой все варианты игрушек.
Одним из вариантов игрушек являются конструкторы. Они выделены голубым овалом. Конструкторы являются отдельным множеством, и, одновременно, частью множества «Игрушки».
Заводные игрушки также являются частью множества «Игрушки», но не относятся к множеству «Конструкторы». Поэтому, они выделяются фиолетовым овалом. А вот множество «Заводных автомобилей» является самостоятельным, но при этом, является подмножеством «Заводных игрушек».
При помощи этого метода ученый решал сложнейшие математические задачи. Применение простых фигур позволяло свести решение любой, даже самой сложной задачи, к символической логике – максимальному упрощению рассуждений.
Позже, данный способ был доработан англичанином Джоном Венном, который ввел понятие пересечения нескольких множеств.
Методика очень проста в использовании — круги Эйлера для дошкольников от 4-5 лет начинают преподавать уже в детском саду. При этом, она же на столько удобна, что применяется даже в высшей академической среде.
Применение кругов Эйлера
Основная цель использования диаграмм – практическое решение задач по объединению или пересечению множеств.
Области применения: математика, логика, менеджмент, статистика, информатика и др. На самом деле, их значительно больше, но перечислить все попросту невозможно.
Диаграммы делятся на два вида.
Первый описывает объединение понятий, вложенность одного в другое. Пример приведен в статье выше.
Второй описывает пересечения двух разных множеств некоторыми общими признаками. Один из примеров
Примеры задач и решения
Рассмотрим задачи, в которых помогают разбираться круги Эйлера, примеры решения задач по логике и математике.
Задачи для дошкольников

Первые в очереди: круги Эйлера для дошкольников, задания с ответами на которые помогут понять, как малыши впервые знакомятся с методикой упрощения сложных математических и логических задач.
Задание №1 – начальный уровень.
Цель: научить ребенка определять предмет, наиболее соответствующий одновременно двум свойствам.
Правильный ответ: кубик Рубика.
Задание №2
Правильный ответ: лягушка.
Задание №3
Правильный ответ: груша.
Задание №4 – средний уровень.
Задания усложняются тем, что используется больше множеств.
Правильный ответ: Солнце.
Задание №5
Правильный ответ: платье.
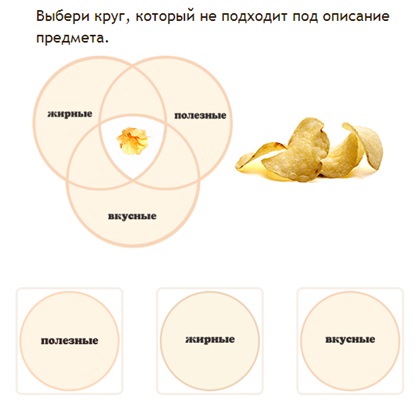
Задание №6
Правильный ответ: полезные.
Задания для школьников
Следующие задачи по логике с ответами, круги Эйлера в которых являются основой для решения, касаются младших школьников. Подобные задания обучают детей разбирать логические пересечения по определенным признакам.
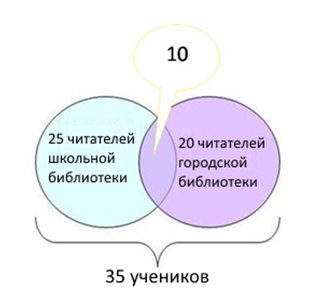
Задание №1
35 учеников зарегистрированы в школьной или городской библиотеках. Из них 25 регулярно посещают школьную библиотеку, а 20 – городскую.
Ответ:
35 – 20 = 15 – левая сектор голубой зоны.
35 – 20 = 15 – также, левый сектор голубой.
Задание №2 – также предназначено для младших классов, но является более сложным.
В 7-А учится 38 человек. Ученики увлекаются разными спортивными играми: 16 – баскетболом, 17 – хоккеем, 18 – футболом. Одновременно баскетбол и хоккей любят 4 человека, баскетбол и футбол – 3, хоккей и футбол – 5, а 3 ученика не интересуются спортом.
Ответ:
Все ученики класса – наибольшая окружность.
Круг «Б» — баскетболисты, «Х» — хоккеисты, «Ф» — футболисты, «Z» — универсальные спортсмены. Трое неспортивных учеников просто находятся в общем круге.
Баскетболисты, входящие в множество «Б», но не входящие в зоны пересечения со множествами «Х» и «Ф».
По аналогии, находим количество хоккеистов.
18 – (3 + Z + 5) = 10 – Z.
Чтобы пределить значение Z, нужно суммировать множества учеников.
3 + (9 – Z) + (8 – Z) + (10 – Z) + 3 + 4 + 5 + Z = 38;
Соответственно, Б = 7, Ф = 8, Х = 6.
Применение круговых диаграмм позволяет наглядно продемонстрировать все взаимоотношения разных групп учеников.
Метод схематического изображения взаимоотношений множеств – не просто увлекательная вещь. Круги Эйлера, примеры решения задач, логика которых неочевидна, показывают, что метод может использоваться не только при развязывании математических заданий, но и находить выход из житейских ситуаций.