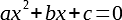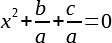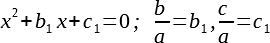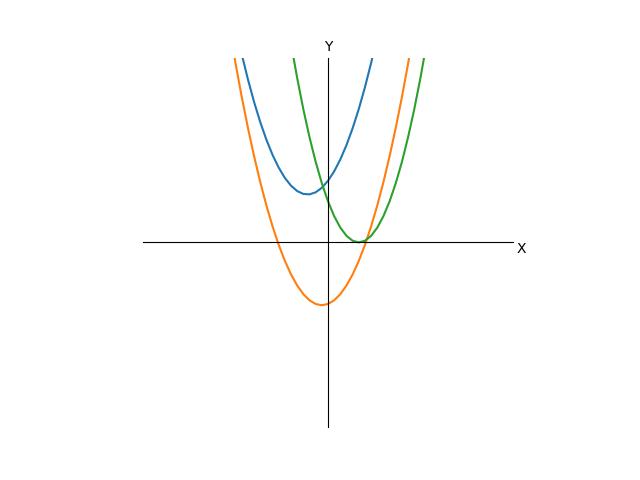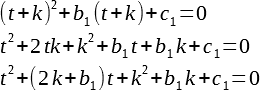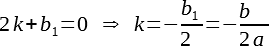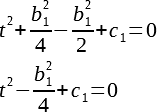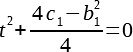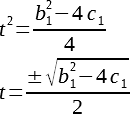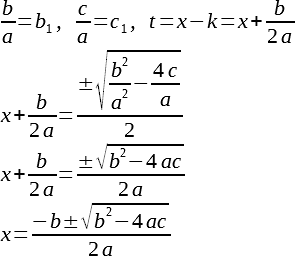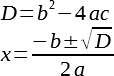Для чего нужны квадратные уравнения

Для чего нужны квадратные уравнения

История квадратных уравнений

Необходимость решать уравнения не только первой степени, но и второй ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков, с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Правила решения этих уравнений, изложенные в вавилонских текстах, совпадает по существу с современными, но в этих текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

Решением квадратных уравнений занимались и в Древней Греции такие ученые как Диофант, Евклид и Герон. Диофант Диофант Александрийский – древнегреческий математик, живший предположительно в III веке нашей эры. Основное произведение Диофанта – «Арифметика» в 13 книгах. Евклид. Евклид древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике Герон. Герон – греческий математик и инженер впервые в Греции в I век н.э. дает чисто алгебраический способ решения квадратного уравнения

Задачи на квадратные уравнения встречаются уже в астрономическом трактате «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученый, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме: ax2 + bх = с, а> 0. (1) В уравнении (1) коэффициенты, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим. В Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.

Вот одна из задач знаменитого индийского математика XII в. Бхаскары.

«Обезьянок резвых стая

А двенадцать по лианам Всласть поевши, развлекалась

Стали прыгать, повисая

Их в квадрате часть восьмая

Сколько ж было обезьянок,

На поляне забавлялась

Ты скажи мне, в этой стае?»

Квадратные уравнения в Европе XVII века

Определение квадратного уравнения

Коэффициенты квадратного уравнения

Какие из данных уравнений не являются квадратными?

Источник

Квадратные уравнения для гуманитариев и школьников.

Ну вот, наконец настало время запилить первый свой познавательный пост.

Все в школе решали квадратные уравнения, там вам рассказывали про дискриминант, что два корня, и все такое, причем, скорее всего, в подробности не вдаваясь. Мне в какой-то момент стало интересно, а почему все так, а не иначе, откуда взялись эти дискриминанты, почему корней два, а не три или сколько-то еще. Вообще, я люблю представлять себя математиком древности, который открывает что-нибудь. Типа, вот раньше чего-то не было, а он взял и вывел. Как это могло происходить?

Конечно, я буду использовать современные достижения математики, которые, возможно, не были известны первооткрывателям тех же квадратных уравнений, но строгости это не уменьшает, поэтому такой подход меня устраивает.

Итак, что же такое квадратное уравнение? Это уравнение вида:

У нас тут общий случай, то-есть неизвестны конкретные значения констант, поэтому честно нарисовать график квадратичной функции сразу мы не можем. Сперва я хотел исследовать функцию всеми доступными методами(дабы аргументированно рисовать график), но потом решил, что, раз для нахождения решения нам нам хватит чисто арифметических действий, лучше не усложнять и не лезть в производные. Поэтому я решил нарисовать несколько графиков, неподходящие из которых мы будем отсеивать по мере продвижения к решению.

Итак, допустим, наша функция будет представлять собой один из графиков, пока мы не знаем, какой.

Теперь, попробуем как-нибудь изменить исходную функцию, чтобы она стала проще, но сохранила свойства исходной. У нас три константы, а это многовато, давайте попробуем избавиться от как можно большего их количества. Для начала, мы можем поделить все уравнение на a. а заведомо не равна нулю, так как если бы была равна, наше уравнение превратилось бы в простое линейное, которое, будем считать, уже всем известно, как решать. Тогда у нас получится новое уравнение:

Чтобы не тащить возможное нагромождение дробей, мы назовем для краткости константы новыми именами, а уравнение преобразуется к виду:

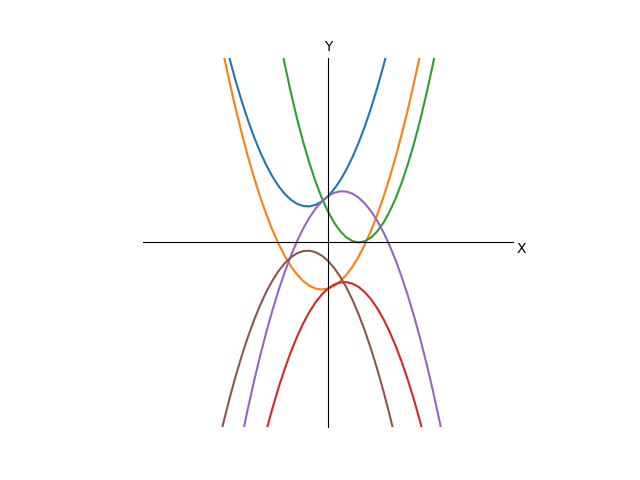
А что там с графиком стало от такого преобразования? По сути, на правую часть уравнения это никак не повлияло, а функция слева сжалась(или растянулась, в зависимости от того, больше модуль а, чем единица, или меньше) пропорционально коэффициенту a к осиX, а если а было отрицательным, то еще и перевернулась вверх ногами. Самое важное здесь для нас то, что пересечение графиков с осью X вообще никак не изменилось, значит, искомое решение уравнения осталось тем же самым. Кроме того, теперь мы можем быть точно уверены, что у новой функции «рога» направлены вверх, ведь х в квадрате теперь с положительным коэффициентом, а значит, при больших по модулю значениях х, как не трудно догадаться, этот член будет положительным и будет расти быстрее, чем оставшиеся два члена.

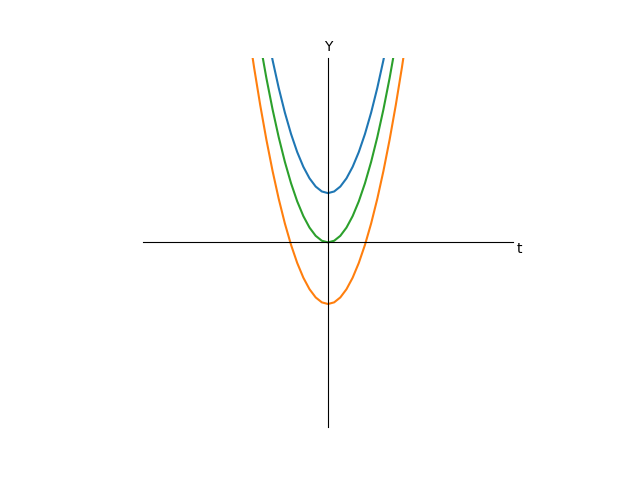
Теперь наши графики буду выглядеть как-то так, мы убрали из них все те, что рогами вниз:

Все внимание на коэффициент перед t в первой степени. Благодаря тому, что мы можем k выбрать произвольно, мы можем сделать так, чтобы этот коэффициент стал равным нулю, а значит, t в первой степени исчезнет из уравнения, и оно еще упростится!

Подставим найденное k в предыдущее выражение, упростим, получим:

Как видно, переменная t осталась только в виде квадрата без коэффициентов, все остальное ушло в одну константу. Но что вообще это преобразование делает с графиком? Оно просто-напросто сдвигает график влево на расстояние k(если k положительное, и в вправо в противном случае). Стало быть, если у нас было пересечение с нулем, то оно и останется, но сдвинется в какую-то сторону, а если не было, то его и не появится. Можно заметить, что если мы поменяем t на -t, то ничего не изменится(квадрат аннигилирует минус), значит, функция стала четной, отражение графика функции от оси Y ничего не меняет, следовательно, преобразование, которое мы сделали, превращает график в симметричный относительно оси Y, причем все линии одинаковые, за исключением того, что находятся на разной высоте.

Рассмотрим повнимательнее последнее выражение, его можно переписать в виде:

Очевидно, что так как t в квадрате может быть только неотрицательным, то минимум функции достигается при t=0. Следовательно, если второе слагаемое(а можно считать, что только его числитель) положительно, то функция до нуля не достанет и решений уравнения, стало быть, нет. Это случай синей кривой на графике. Если нам так повезло, что что слагаемое равно нулю, то очевидным единственным решением будет 0, это зеленая кривая. Если же слагаемое отрицательно, то существуют какие-то решения, это оранжевая кривая. Это три случая, имеют принципиальную разницу, все остальное многообразие возможных уравнений сводится к этим трем. Теперь разберемся, сколько же там корней. Выразим t из последнего выражения(будем считать, что обратную функцию для квадрата мы знаем):

Но мы нашли какое-то t, а нам ведь надо найти х. Для этого, выполним все преобразования, которые мы сделали над уравнением, теперь уже над его решением в обратном порядке, а именно просто подставим все то, что мы назаменяли:

Ой, а что это у нас тут под корнем такое знакомое. Да это же дискриминант!

Ну вот, собственно, и все, решение получено. Хотел еще про правила Виета написать, но, думаю не стоит, пост и так большой, а правила эти весьма просты.

Источник

квадратные уравнения. зачем?

какие практические задачи обыватель может свести к квадратному уравнению?

Это смотря, что за обыватель.

Все задачи обывателя решит специализированное ПО в его мозговом импланте айфоне.
Обывателю не обязательно быть знакомым ни с азами биологии, ни с азами химии, ни с азами физики, ни с азами астрономии, ни с азами географии, геологии, истории, экономики, права, etc.
Нужно только уметь читать короткие фразы и тыкать грязным пальцем в иконки.

Но вот если ты хочешь воспитать не обывателя-потреблядину, а человека-творца, то квадратные уравнения станут ценной крупинкой в его картине мироздания.

Например задачи, в которых возникает теорема Пифагора

рассчёт траектории кинутого камня, например

эээ извелечение корня это всё таки очень частный случай.

или есть задача(практическая) с теоремой Пифагора в которой

сложные проценты, амортизация оборудования, катание с горки, стрельба навесом, прыжок с окна 🙂 примеры см в школьных учебниках физики и математики;

то что люди с психикой испорченной математикой сводят к дифурам, простые люди сводят по возможности к более понятным степенным уравнениям, причём даже не заморачиваются их формальным написанием..или забивают болт 🙂

рассчёт траектории кинутого камня, например

Не смеши. Когда ты на практике швыряешь камни, меньше всего ты думаешь об уравнениях. Тем более ты не думаешь о них, когда играешь в энгри бёрдз.

Источник

Урок по алгебре «Квадратные уравнения в нашей жизни». 8 класс.

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 19

г. Димитровград
Ульяновская область

УРОК АЛГЕБРЫ

« КВАДРАТНЫЕ УРАВНЕНИЯ В НАШЕЙ ЖИЗНИ »

Подготовила и провела

Егорычева Оксана Юрьевна

Тема: «Квадратные уравнения в нашей жизни».

Предмет математики настолько серьезен, что полезно не упускать случая, делать его немного занимательным.

I . Организационный момент:

Добрый день дорогие друзья, гости! Я рада приветствовать Вас на нашем уроке, и прошу всех вас улыбнуться друг другу, а ребят прошу, мысленно пожелать успехов и себе и товарищам. Садитесь.

Сегодняшний урок мы проведем с использованием рейтинговой системы контроля знаний. У вас имеются оценочные листы, в которых вы выставляете баллы, полученные за каждый этап урока. Каждый правильный ответ оценивается в 1 балл.

На доске уравнение: 15х 2 + х + 2019 = 0

— Назовите вид данного уравнения. Назовите его коэффициенты.

О каком событии говорят коэффициенты уравнения? (Дата проведения урока)

— Как вы знаете, вчера мы встретили Старый новый год. А по китайскому календарю этот год будет годом свиньи. Поэтому сегодня мы будем решать задачу об этих славных животных.

Подготовьтесь к выразительному чтению задачи.

Вопрос: С чего придется начать, чтобы ответить на вопрос задачи? (Составить уравнение)

Что необходимо для составления уравнения? (ввести неизвестную)

Что мы обозначим за х? (количество всех поросят)

Как обозначить часть восьмую поросят?

А в квадрате? () 2

Что еще известно о поросятах? (12 поросят в луже тёпленькой лежат)

А как узнать, сколько их всего было? (() 2 + 12)

D ₁ = k ²- ac ; Х=

Х= S = a • b .

Поросят весёлых стая,

Всласть поевши, развлекалась.

Часть восьмая их в квадрате

Хрюкала и забавлялась.

А двенадцать поросят

В луже тёпленькой лежат.

Ты скажи мне поскорей,

Сколько было всех свиней?

Самостоятельно составьте уравнение. Сравните его.

Какой вид оно имеет? (квадратное)

Слайд 5

Эта задача подвела нас к теме урока.

Сформулируйте тему нашего урока. (Учащиеся формулируют тему)

Я бы хотела уточнить. Сегодня мы убедимся, что без умения решать квадратные уравнения, невозможна жизнь современного человека.

Тема урока: Квадратные уравнения в нашей жизни.

Запишите её в рабочих листах.

Чтобы урок для вас стал полезен, поставьте перед собой цель работы и запишите её в рабочем листе, выбрав один из вариантов.

-Какие цели мы поставим к уроку? (вспомним и обобщим все те знания, которые мы получили на предыдущих уроках).

— Ребята, скажите, что должен уметь делать каждый из вас на сегодняшнем уроке? (уметь правильно, быстро и рационально решать квадратные уравнения)

Слайд 6

2. Актуализация знаний.

Слайд 7

1. Какое же уравнение называется квадратным уравнением? (ах 2 + вх + с =0)

2.Как называются числа а, в и с в квадратном уравнении.

4.Как называются квадратные уравнения, у которых хотя бы один из коэффициентов в или с =0 (неполное)

5. Что нам необходимо чтобы решить полученное нами уравнение в задаче? (дискриминант).

6.Какие формулы для его нахождения вам известны? (в презентации)

Теперь мы уже готовы к решению нашей задачи.

Слайд 8

Какое будет первое действие?

Ребята, все согласны?

Класс внимание, может у кого- то есть другое предложение?

Какой способ лучше? Пойдем через к. Вычисления меньше.

Решение задачи. (Каждая строка в решении, новый ученик у доски получает жетон.)

1 человек () 2 + 12 = х

+ 12 = х

Д_{1 = К} 2 – ас = 256 = 16 2

Слайд 9

Ребята, мы решили задачу, но у нас возникла проблема, как это часто бывает в жизни. Куда же нам поместить наших поросят? Ответ на этот вопрос нам дадут квадратные уравнения.

Ведь благодаря им рассчитывается тормозной путь автомобиля, мощность ракеты для выхода на орбиту и даже строятся любые объекты, в том числе свиноферма. Поэтому дружно встали и идем на строительство. Я выдаю вам кирпичи. Ваша задача – передать его сзади стоящему человеку, а потом с конца вернуть таким же образом вперёд. Побеждает та бригада, которая вернет кирпич первой.

Мы пришли на объект. Садитесь.

Слайд 10

Слайд 11

Слайд 12

(Пусть одна сторона х, другая х +6, а так как площадь 135 м 2 имеем уравнение)

Слайд 13

1 ученик х ( х+6) = 135

Класс решает самостоятельно, а у доски 2 ученик сам.

тогда вторая сторона 6+9 = 15

Слайд 14

Итак, наш участок имеет размеры 9 на 15 метров. На нём обживаются поросята, а я предлагаю узнать имя еще одного ученого.

Вопросы по способам решения квадратных уравнений (предложить более рациональный способ решения)

1.Какое уравнение можно решить извлечением квадратных корней? (Д)

2. Какое уравнение решается вынесением общего множителя за скобки? (И)

3. Какое уравнение можно решить, представляя в виде квадрата двучлена? (О)

4. В каком уравнении надо применять общую формулу корней? (Ф)

5. Какое уравнение решается по формуле, используя четный второй коэффициент? (А)

6. Какое уравнение удобно решать по теореме Виета? (Н)

7. Какое уравнение можно решить разложением разности квадратов? (Т)

Итак, мы сегодня открыли свиноферму, заселили туда поросят. И все это благодаря чему? (квадратным уравнениям, которые к нам пришли из древности.)

4. Ребята, прочитайте на историческую справку.

Слайд 19

Квадратные уравнения впервые встречаются в работе индийского математика и астронома Ариабхатты.

Другой индийский ученый Брахмагупта ( VII в) изложил общее правило решения квадратных уравнений, которое практически совпадает с современным.

В Древней Индии были распространены публичные соревнования в решении трудных задач.

Часть из которых благодаря вам решена на нашем уроке.

5. Подведем итог. Подсчитаем жетоны. У кого 4 жетона, ставьте в рабочем листе оценку «4», у кого 5 жетонов – ставим «5». А теперь обещанный сюрприз: выбираем руководителя фермы? (Вручить медаль)

Наш урок подходит к концу. И в завершение я хочу рассказать вам одну притчу.

Шел мудрец, а навстречу ему три строителя, которые везли под горячим солнцем тележки с камнями. Он остановил их и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?». Тот с грустью ответил, что целый день возил эти тяжелые камни. У второго спросил: «А что ты делал целый день?» Тот ответил: «Я добросовестно выполнял свою работу» А третий улыбнулся, его лицо засветилось радостью и удовольствием: «а я принимал участие в строительстве храма»

Мы с вами тоже были строителями.

А теперь оцените свою работу на уроке.

Перед вами рисунки (слайд). Выберите себе тот, который характеризует вашу степень участия на уроке.

Кто работал как первый человек, т.е. решал весь урок эти непонятные, трудные уравнения? Поднимите руку. А почему?

Кто работал как второй человек, т.е. добросовестно решал все уравнения?

Кто работал как третий человек, т.е. приумножал свои знания? – 3 рисунок

(Учащиеся обосновывают свой выбор)

Каждый из вас в начале урока, поставил перед собой цель. Поднимите руки те, кто достиг своей цели. Назовите свою цель. А что ты делал для достижения цели. (Решал задачи, применял формулы.)

Что вам понравилось? Какой момент урока был трудным? Где были затруднения? Почему? Что для себя узнал нового на уроке?

— Вы славно потрудились! Я осталась довольна вами. Спасибо за урок! Всего доброго.

1. Задача: Можно ли в котлован круглой формы диаметром 1,6 м поместить ёмкость для бассейна прямоугольной формы со сторонами равными корням данного уравнения

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

2. Творческое задание. Подготовить сообщение о Диофанте.

Приложение №1 РАБОЧИЙ ЛИСТ

Цель: а) Я хочу научиться…______________________________________

б)Я хочу узнать…_____________________________________________

D ₁ = k ²- ac ; Х=

Х= S = a • b .

Поросят весёлых стая,

Всласть поевши, развлекалась.

Часть восьмая их в квадрате

Хрюкала и забавлялась.

А двенадцать поросят

В луже тёпленькой лежат.

Ты скажи мне поскорей,

Сколько было всех свиней?

Задание3: Узнать имя еще одного ученого.

Вопросы по способам решения квадратных уравнений (предложить более рациональный способ решения)

1.Какое уравнение можно решить извлечением квадратных корней?

2. Какое уравнение решается вынесением общего множителя за скобки?

3. Какое уравнение можно решить, представляя в виде квадрата двучлена?

4. В каком уравнении надо применять общую формулу корней?

5. Какое уравнение решается по формуле, используя четный второй коэффициент?

6. Какое уравнение удобно решать по теореме Виета?

7. Какое уравнение можно решить разложением разности квадратов?

_ _________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Количество Моя

«Лист настроения» : отметить, с каким настроением вы пришли на урок и с каким ушли с урока.

Источник