Для чего нужны мнимые числа

Откуда есть пошло комплексное число

В современной математике комплексное число является одним из фундаментальнейших понятий, находящее применение и в «чистой науке», и в прикладных областях. Понятно, что так было далеко не всегда. В далекие времена, когда даже обычные отрицательные числа казались странным и сомнительным нововведением, необходимость расширения на них операции извлечения квадратного корня была вовсе неочевидной. Тем не менее, в середине XVI века математик Рафаэль Бомбелли вводит комплексные (в данном случае точнее сказать, мнимые) числа в оборот. Собственно, предлагаю посмотреть, в чем была суть затруднений, доведших в итоге солидного итальянца до подобных крайностей.

Существует распространенное заблуждение, что комплексные числа потребовались для того, чтобы решать квадратные уравнения. На самом деле, это совершенно не так: задача поиска корней квадратного уравнения никоим образом введение комплексных чисел не мотивирует. Вот совершенно.

Давайте убедимся сами. Всякое квадратное уравнение можно представить в виде:
.
Геометрически, это означает, что мы хотим найти точки пресечения некоторой прямой и параболы
Я тут даже картинку сделал, для иллюстрации.

Как нам всем хорошо известно из школы, корни квадратного уравнения (в указанных выше обозначениях) находятся по следующей формуле:

Оказываются возможными 3 варианта:
1. Подкоренное выражение положительно.
2. Подкоренное выражение равно нулю.
3. Подкоренное выражение отрицательно.

В первом случае имеются 2 различных корня, во втором два совпадающих, в третьем уравнение «не решается». Все эти случаи имеют вполне наглядную геометрическую интерпретацию:
1. Прямая пересекает параболу (синяя прямая на рисунке).
2. Прямая касается параболы.
3. Прямая не имеет с параболой общих точек (сиреневая прямая на рисунке).

Ситуация проста, логична, непротиворечива. Пытаться извлекать квадратный корень из отрицательного числа нет совершенно никаких оснований. Никто и не пытался.

Обстановка существенно изменилась, когда пытливая математическая мысль добралась до кубических уравнений. Чуть менее очевидно, используя некоторую несложную подстановку, всякое кубическое уравнение можно свести к виду: . С геометрической точки зрения ситуация похожа на предыдущую: мы ищем точку пересечения прямой и кубической параболы.
Взгляните на картинку:

Существенное отличие от случая квадратного уравнения в том, что какую бы прямую мы не взяли, она всегда пересечет параболу. Т.е., уже из чисто геометрических соображений, кубическое уравнение всегда имеет хотя бы одно решение.
Найти его можно воспользовавшись формулой Кардано:

где
.
Немного громоздко, но пока, вроде бы, все в порядке. Или нет?

Вообще, формула Кардано — это яркий пример «принципа Арнольда» в действии. И что характерно, Кардано никогда на авторство формулы не претендовал.

Вернемся, однако, к нашим баранам. Формула замечательная, без преувеличение великое достижение математики начала-середины XVI века. Но есть у нее один нюанс.
Возьмем классический пример, который рассматривал еще Бомбелли:
.
Внезапно,
,
и, соответственно,
.
Приплыли. А формулу жалко, а формула-то хорошая. Тупик. При том, что решение у уравнения, безусловно, есть.

Идея Рафаэля Бомбелли заключалась в следующем: давайте прикинемся шлангом и сделаем вид, что корень из отрицательного — это какое-то число. Мы, конечно, знаем, что таких чисел нет, но тем не менее, давайте представим, что оно существует и его, как обычные числа, можно складывать с другими, умножать, возводить в степень и т.п.

Используя подобный подход, Бомбелли установил, в частности, что
,
и
.
Давайте проверим:
.
Заметьте, в выкладках никаких предположений о свойствах квадратных корней из отрицательных чисел не предполагалось, кроме упомянутого выше допущения, что они ведут себя как «обычные» числа.

В сумме получаем . Что вполне себе правильный ответ, который элементарно проверяется прямой подстановкой. Это был настоящий прорыв. Прорыв в комплексную плоскость.

Тем не менее, подобные выкладки выглядят как некоторая магия, математический фокус. Отношение к ним, как к некоему трюку, сохранялось среди математиков еще очень долго. Собственно, придуманное Рене Декартом для корней из отрицательных название «мнимые числа» вполне отражает отношение математиков тех времен к таким развлечениям.

Однако, время шло, «трюк» применялся с неизменным успехом, авторитет «мнимых чисел» в глазах математического общества рос, сдерживаемый, однако, неудобством их использования. Лишь получение Леонардом Эйлером (кстати, это именно он ввел ныне общеупотребительное обозначение для мнимой единицы) знаменитой формулы

открыло комплексным числам дорогу в самые различные области математики и ее приложений. Но это уже совсем другая история.

Источник

Мнимые числа для описания реальности?

Новый мысленный эксперимент показывает, что квантовая механика не работает без странных чисел, которые становятся отрицательными при возведении в квадрат.

Много веков назад математики были обеспокоены, когда обнаружили, что вычисление свойств определенных кривых требует, казалось бы, невозможного: чисел, которые при умножении сами на себя становятся отрицательными.

Однако физики, возможно, только что впервые показали, что мнимые числа в определенном смысле вещественны.

Группа теоретиков в области квантовой физики разработала эксперимент, результат которого зависит от того, есть ли у природы мнимая сторона. При условии, что квантовая механика верна — предположение, с которым мало кто поспорит, — аргумент команды по существу гарантирует, что комплексные числа являются неизбежной частью описания материальной вселенной.

«Эти комплексные числа обычно являются просто удобным инструментом, но здесь оказывается, что они действительно имеют какое-то материальное значение», — сказал Тамаш Вертези, физик из Института ядерных исследований Венгерской академии наук, который много лет назад утверждал обратное. «Мир таков, что ему действительно нужны эти комплексные числа», — сказал он.

В квантовой механике поведение частицы или группы частиц выражается волнообразным объектом, известным как волновая функция или ψ. Волновая функция прогнозирует вероятные результаты измерений, такие как вероятное положение или импульс электрона. Так называемое уравнение Шрёдингера описывает, как волновая функция изменяется во времени — и это уравнение включает i.

Физики никогда не знали, что с этим делать. Когда Эрвин Шрёдингер вывел уравнение, которое теперь носит его имя, он надеялся избавиться от i. «Что неприятно и против чего прямо следует возражать, так это против использования комплексных чисел, — писал он Хендрику Лоренцу в 1926 году, — Ψ, безусловно, является вещественной функцией».

Желание Шрёдингера, безусловно, было правдоподобным с математической точки зрения: любое свойство комплексных чисел может быть зафиксировано комбинациями вещественных чисел, а также новыми правилами, открывая математические возможности полностью вещественной версии квантовой механики.

Действительно, переход оказался достаточно простым, так что Шрёдингер почти сразу открыл то, что он считал «истинным волновым уравнением», которое «сторонилось» i. «Еще один камень с души упал», — написал он Максу Планку менее чем через неделю после своего письма Лоренцу. Все вышло именно так, как хотелось.

Но использование вещественных чисел для моделирования сложной квантовой механики неудобное и абстрактное занятие, и Шрёдингер признал, что его полностью вещественное уравнение слишком громоздко для повседневного использования. В течение года он описывал волновые функции как комплексные, в том виде, в каком их представляют сегодня физики.

«Любой, кто хочет выполнить работу, использует комплексное описание», — сказал Мэтью МакКейг, учёный в области информатики из Технологического университета Квинсленда в Австралии.

Однако формулировка квантовой механики с помощью вещественных чисел сохранилась как свидетельство того, что комплексная версия просто необязательна. Например, команды, включая Вертези и МакКейга, показали в 2008 и 2009 годах, что и без i они могут идеально предсказать результат известного эксперимента в квантовой физике, известного как тест Белла.

Новое исследование, которое было опубликовано на сервере научных препринтов arxiv.org в январе, обнаружило, что ранние предложения по тестам Белла просто недостаточно продвинулись, чтобы опровергнуть версию квантовой физики с вещественными числами. Это исследование предлагает более сложный эксперимент Белла, который, похоже, требует комплексных чисел.

Ранние исследования привели людей к выводу, что «в квантовой теории комплексные числа лишь удобны, но не необходимы», — писали авторы, в число которых входят Марк-Оливье Рену из Института фотонных наук в Испании и Николя Жизен из Женевского университета. «Мы доказываем ошибочность этого вывода».

Группа отказалась публично обсуждать свою работу, поскольку он все еще находится на экспертной оценке.

Тест Белла показывает, что пары удаленных друг от друга частиц могут обмениваться информацией в едином «запутанном» состоянии. Если бы монета 25 центов в штате Мэн могла «запутаться», например, с такой же монетой в Орегоне, то повторяющиеся подбрасывания показали бы, что всякий раз, когда одна монета падает орлом, ее дальний партнер, как ни странно, выпадет решкой. Точно так же в стандартном эксперименте теста Белла запутанные частицы отправляются двум физикам с вымышленными именами Алиса и Боб. Они измеряют частицы и, сравнивая измерения, обнаруживают, что результаты коррелированы таким образом, что это не поддаётся объяснению, разве что частицы обмениваются информацией.

Модернизированный эксперимент добавляет второй источник пар частиц. Одна пара достается Алисе и Бобу. Вторая пара, «родом» из другого места, отправляется Бобу и третьему лицу, Чарли. В квантовой механике с комплексными числами частицы, которые получают Алиса и Чарли, не обязательно должны быть запутаны друг с другом.

Однако никакое описание в виде вещественных чисел не может воспроизвести модель корреляций, которую будут измерять три физика. В новой статье показано, что рассмотрение системы как вещественной требует введения дополнительной информации, которая обычно находится в мнимой части волновой функции. Частицы Алисы, Боба и Чарли должны разделять эту информацию, чтобы воспроизводить те же корреляции, что и в стандартной квантовой механике. И единственный путь приспособиться к этому разделению — это перепутать все их частицы друг с другом.

В предыдущих воплощениях теста Белла электроны Алисы и Боба поступали из одного источника, поэтому дополнительная информация, которую они должны были нести в описании вещественных чисел, не представляла проблемы. Но в тесте Белла с двумя источниками, где частицы Алисы и Чарли происходят из независимых источников, фиктивная трехсторонняя запутанность не имеет физического смысла.

Даже без привлечения Алисы, Боба и Чарли для фактического проведения эксперимента, который представляет новая статья, большинство исследователей крайне уверены, что стандартная квантовая механика верна и, следовательно, эксперимент найдет ожидаемые корреляции. Если это так, то одни только вещественные числа не могут полностью описать природу.

«В статье устанавливается, что существуют истинные комплексные квантовые системы», — сказал Вальтер Моретти, физик-математик из Университета Тренто в Италии. Этот результат стал для него совершенно неожиданным.

Тем не менее велика вероятность того, что когда-нибудь эксперимент состоится. Это будет непросто, но технических препятствий нет. И глубокое понимание поведения усложняющихся квантовых сетей будет становиться все более актуальным, поскольку исследователи продолжают связывать многочисленные Алисы, Бобы и Чарли через возникающие квантовые сети.

«Поэтому мы верим, что опровержение вещественной квантовой физики произойдет в ближайшем будущем», — пишут авторы.

Источник

Введение в комлексные числа

Выяснив, что многие знакомые программисты не помнят комплексные числа или помнят их очень плохо, я решил сделать небольшую шпаргалку по формулам.

А школьники могут что-то новое узнать 😉
// Всех кого заинтересовал прошу под кат.

Итак, комплексные числа эта такие числа, которые можно записать как

Где x, y вещественные числа(т.е привычные всем числа), а i — число, для которого
выполняется равенство

x называется действительной частью, y — мнимой.

Это алгебраическая форма записи комплексного числа.

Существует также тригонометрическая форма записи комплексного числа z:

С введением, пожалуй, все.

Переходим к самому интересному — операциям над комплексными числами!
Для начала рассмотрим сложение.

У нас есть два таких комплексных числа:

Как же их сложить?
Очень просто: сложить действительную и мнимую части.
Получим число:

Все просто, не так ли?
Вычитание выполняется аналогично сложению.
Нужно просто вычесть из действительной части 1 числа действительную часть 2 числа,
а потом проделать тоже с мнимой частью.
Получим число

Умножение выполняется вот так:

Напомню, x это действительная часть, y — мнимая.
Деление выполняется вот так:

Кстати, поддержка комплексных чисел есть в стандартной библиотеке Python:

Вместо i используется j.
Кстати, это потому что Python принял конвенцию инженеров-электриков, у которых
буква i обозначает электрический ток.
Задавайте свой вопросы, если они есть, в комментариях.
Надеюсь, вы узнали для себя что-то новое.

UPD: В комментариях просили рассказать о практическом применении.
Так вот комплексные числа нашли широкое практическое применение в авиации
(подъемная сила крыла) и в электричестве.
Как видете, очень нужная вещь 😉

Источник

Мнимые числа

Если бы мы жили несколько тысяч лет тому назад, мы бы, несомненно, предсказали открытие мнимых чисел, поскольку действительные числа – это лишь принадлежащие к общепринятой реальности варианты того, что мы переживаем, когда наблюдаем и считаем. Если бы мы жили в далеком прошлом и понимали, что числа символизируют не только явные процессы, но и тонкие процессы, которые не выявляются непосредственно, мы бы, вероятно, подумали, что нам необходимо новое описание событий, которое включает в себя действительные числа, а также что-то наподобие «воображаемых» чисел, чтобы описывать аспекты событий, относящиеся как к ОР, так и к НОР.

После открытия мнимых чисел в XVI и XVII вв. оказалось, что эти числа не настолько мнимые, как первоначально думали математики, однако эти числа все-таки дают нам понимание НОР-аспектов природы и, конечно, нашей собственной природы. Более того, нам очень важно исследовать эти числа, так как они образуют основу описания квантовой физики и теории относительности. Современная физика не может существовать без мнимых чисел.

Как видно из терминов «рациональный» и «иррациональный», открытие чисел с самого начала осложнялось вопросом о том, откуда происходят эти удивительные символы и что они собой представляют. Когда в эпоху Возрождения Готфрид Лейбниц и другие разрабатывали мнимые числа для решения проблем в математике, понятие мнимых чисел также считалось бесплотным. Мнимые числа сравнивали с духами: они присутствовали, но их было невозможно увидеть.

Формальный способ записи мнимых чисел состоит в помещении после действительного числа буквы i [12]. Например, если действительное число 4 написать как 4i, то оно будет обозначать мнимое число.

Что же в действительности представляют собой мнимые числа? Вспомните, что действительные числа кодируют, но маргинализируют переживания НОР Многие из конкретных и наблюдаемых свойств вещей, которые мы считаем, не учитываются действием простого счета. Из-за процесса маргинализации, действительных чисел никогда не будет достаточно для полного описания событий, поэтому в математике, наряду с общепринятыми количествами, вроде 1, 2 и 3, нам требуется нечто вроде воображаемых или необщепринятых качеств. Будучи полезными, мнимые числа также указывают назад, на магические качества, которые люди нередко ассоциируют с числами.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Читайте также

8. МНИМЫЕ ДОВОДЫ В ПОЛЬЗУ РЕЛЯТИВИЗМА

8. МНИМЫЕ ДОВОДЫ В ПОЛЬЗУ РЕЛЯТИВИЗМА Многие условия содействуют распространенности релятивистического учения о ценностях, т.е. учения, согласно которому все ценности относительны. Прежде всего следует иметь в виду, как это уже было разъяснено, что неорганическое

Противоречия мнимые и реальные

Противоречия мнимые и реальные Полемическая заметка Ильенкова в «Литературной газете» (1969) Доктор П. Медавар отмечает две болезни в современной духовной культуре — «поэтизм» и «сциентизм» (от латинского «scientia» — наука). «Поэтизм», по его определению, — это

Числа на барабане

Числа на барабане Некий мистер Ли Таврос, мастер по изготовлению музыкальных инструментов, однажды попытался оживить свой бизнес «барабанной дробью» — с помощью загадок на числа. Во время ежегодного съезда собратьев по ремеслу он, стремясь привлечь публику к своему

К. МАРКС и Ф. ЭНГЕЛЬС МНИМЫЕ РАСКОЛЫ В ИНТЕРНАЦИОНАЛЕ

К. МАРКС и Ф. ЭНГЕЛЬС МНИМЫЕ РАСКОЛЫ В ИНТЕРНАЦИОНАЛЕ ЗАКРЫТЫЙ ЦИРКУЛЯР ГЕНЕРАЛЬНОГО СОВЕТА МЕЖДУНАРОДНОГО ТОВАРИЩЕСТВА РАБОЧИХ[1]Написано К. Марксом и Ф. Энгельсом между серединой января — 5 марта 1872 г. Напечатано в виде брошюры в Женеве в 1872 г.Печатается по тексту

Глава VII. СИМВОЛИЧЕСКИЕ ЧИСЛА

Глава VII. СИМВОЛИЧЕСКИЕ ЧИСЛА Прежде чем перейти к рассмотрению теории космических циклов, мы должны сделать несколько замечаний о роли символики чисел в произведении Данте. В работе профессора Родольфо Бенини[58] мы нашли об этом очень интересные замечания, однако он не

Числа

Числа Авторитет Фурье, Референция, Цитата, Наука, предшествующий Дискурс, позволяющий ему говорить и самому обладать властью над «глупостью 25 ученых веков, которые об этом и не думали», есть расчет (как сегодня для нас — формализация). Этому расчету нет необходимости быть

ОБЩАЯ ТЕОРИЯ ЧИСЛА

ОБЩАЯ ТЕОРИЯ ЧИСЛА § 10. Вступление.Число является настолько основной и глубокой категорией бытия и сознания, что для его определения и характеристики можно брать только самые первоначальные, самые отвлеченные моменты того и другого. Математика— наука о числе—есть уже

Числа и рекурсия

Числа и рекурсия Благодаря восприятию множественности разум становится разумным. Люди умеют считать, различают объекты и ощущают одинаковость. Последовательный счёт и математические способности являются высшими феноменами, вершиной айсберга, которая опирается на

ФИЛОСОФИЯ ЧИСЛА

ФИЛОСОФИЯ ЧИСЛА «Жизнь подобна игрищам: иные приходят на них состязаться, иные — торговать, а самые счастливые — смотреть; так и в жизни: иные, подобно рабам, рождаются жадными до славы и наживы, между тем как философы — до единой только истины», — так говорил Пифагор (584 —

Числа, отличные от натуральных

Числа, отличные от натуральных В предыдущих параграфах мы рассматривали действия над натуральными числами и отметили тот замечательный факт, что машина Тьюринга может оперировать с натуральными числами произвольной величины, несмотря на то, что каждая машина имеет

Действительные числа

Действительные числа Напомним, что натуральные числа являются целыми величинами:0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…Это самый элементарный и фундаментальный вид чисел. Ими можно количественно измерить любую дискретную сущность: можно говорить о двадцати семи овцах в поле, двух

Комплексные числа

Комплексные числа Оказывается, что действительные числа — это не единственная математически мощная и изящная система чисел. Система действительных чисел все же не лишена некоторых неудобств. Например, квадратные корни можно извлекать только из положительных чисел (или

Числа, идущие назад

Числа, идущие назад Современному шаману – а потенциально мы все современные шаманы, наследники и научной, и традиционной мудрости – очень важно развертывать свой процесс, быть свободнее, воплощать его в повседневной жизни. Но это, как правило, заставляет нас забывать,

ЧИСЛА КАК ПОЛЯ

ЧИСЛА КАК ПОЛЯ Прежде чем думать о полях в математике, физике и психологии, давайте рассмотрим повседневное употребление термина «поле». Большинство из нас представляют себе поле как часть земли, выделенную для того или иного использования, например в качестве пастбища

Комплексные числа

Комплексные числа При добавлении мнимых чисел к полю действительных чисел их описательные способности увеличиваются. Получающаяся смесь действительных и мнимых чисел называется комплексными числами. Комплексные числа представляют собой сочетание действительных и

Источник

Что такое комплексные числа

Первый урок по комплексным числам. Сегодня мы разберём:

Если же вас интересует тригонометрическая форма записи комплексного числа, либо извлечение корней из комплексных чисел — этим темам посвящены отдельные уроки.

Сегодня — лишь самое главное. Но не самое простое.:)

0. Краткая вводная

Когда-то нам хватало натуральных чисел:

Всё было прекрасно: «У тебя 5 бананов, у меня ещё 3 — итого у нас 5 + 3 = 8 бананов». Сумма двух натуральных чисел всегда даёт новое натуральное число (говорят, что операция сложения замкнута на множестве натуральных чисел).

Но вот на сцену выходит вычитание — и натуральных чисел стало недостаточно. Например разность 3 − 5 = −2 уже не будет натуральным. Так появились целые числа (натуральные, им противоположные и ноль):

Дальше к делу подключились операции умножения и деления. Да, произведение двух целых чисел всё ещё целое, но вот деление приводит к образованию дробей. Например, 1 : 2 или 5 : 4 уже нельзя записать целым числом. Так появилось множество рациональных чисел или множество дробей:

Это был настоящий триумф для древней математики, и в тот момент казалось, что ничего больше уже изобрести нельзя. Да и зачем?

Проблема пришла откуда не ждали. В какой-то момент классическое умножение «разрослось» до возведения в степень:

Тут-то и выяснилось, что возведение рационального числа в натуральную степень всё ещё будет рациональным числом. Но вот обратная операция — извлечение корня — выносит нас за пределы рациональных чисел:

\[\sqrt<2>=1,41421. \notin \mathbb\]

Так появилось множество действительных чисел — множество бесконечных десятичных дробей, которые могут быть периодическими (и тогда это обычное рациональное число) и непериодическими (такие числа называют иррациональными, и их неизмеримо больше).

Казалось бы: ну вот теперь точно всё! Что ещё нужно для счастья? Проблема в том, что на множестве действительных чисел нельзя извлечь даже самый простой квадратный корень из отрицательного числа:

Однако законы физики (особенно электродинамика и вообще всё, где есть слово «динамика») как бы намекали, что множество содержательных процессов протекает там, где привычные корни не извлекаются. А значит, следует расширить множество действительных чисел так, чтобы такие корни всё же извлекать.

И тут открылись врата в Ад.

1. Комплексная единица

Начнём с ключевого определения.

Однако в остальном это такое же число, как и все остальные. Комплексные единицы можно складывать, умножать, их можно комбинировать с «нормальными» числами:

2. Стандартная форма записи комплексных чисел

А теперь всё по-взрослому.

Определение. Комплексное число — это любое число вида

\[\begin & z=5+3i \\ & \operatorname\left( z \right)=5 \\ & \operatorname\left( z \right)=3 \\ \end\]

\[\begin & 5=5+0\cdot i \\ & x=x+0\cdot i\left( \forall x\in \mathbb \right) \\ \end\]

И напротив: существуют «чисто мнимые» числа, у которых вообще нет действительной части. Та же комплексная единица, например:

\[\begin i &=0+1\cdot i \\ 35i &=0+35\cdot i \\ \end\]

Таким образом, действительные числа являются частным случаем комплексных. Подобно тому как рациональные числа являются частным случаем действительных (в конце концов, рациональные числа — те же десятичные дроби, но с дополнительным условием: они периодические).

2.1. Равенство комплексных чисел

В самом деле, пусть некоторое число записано двумя способами:

Соберём все действительные слагаемые слева, а мнимые — справа:

Слева мы видим действительное число. Значит, справа тоже должно стоять действительное число. Единственная ситуация, в которой это возможно:

Получается, что справа от знака равенства стоит ноль. Следовательно, слева тоже ноль:

Следовательно, исходные записи совпадают.

Поэтому имеет смысл следующее определение.

Определение. Два комплексных числа равны друг другу тогда и только тогда, когда равны их действительные части, а также равны их мнимые части:

Если хотя бы одна из частей не равна, то и сами числа не равны.

Поскольку от перестановки слагаемых сумма не меняется (сложение чисел — настолько суровая операция, что какие-то там «комплексные единицы» никак не нарушают его коммутативности), мы можем записать:

А вот перестановка мнимой и действительной части (если эти части разные) немедленно ведёт к нарушению равенства:

К координатной плоскости мы ещё вернёмся. А пока определим правила сложения и вычитания комплексных чисел.

3. Сложение и вычитание комплексных чисел

Выше мы проводили аналогию между комплексными числами и многочленами. Идём по этому пути дальше и вспоминаем, что многочлены можно складывать, группируя слагаемые и приводя подобные:

Точно так же можно определить и сложение (да и вычитание) двух комплексных чисел. Всё просто:

Другими словами, при сложении комплексных чисел отдельно складываются их действительные части и отдельно — мнимые. То же самое для вычитания.

Не нужно учить эти формулы. Дальше будут формулы умножения и деления — они ещё сложнее. Нужно понять ключевую идею: мы работаем с комплексными числами точно так же, как с многочленами. С небольшим дополнением: все степени комплексной единицы выше первой «сжигаются» прямо по определению самой единицы:

Небольшое замечание. В отличие от математики 5—6 классов, в серьёзной «взрослой» алгебре нет такого понятия как «вычитание». Зато есть понятие противоположного элемента и алгебраической суммы:

Всё это в полной мере относится и к комплексным числам. Там тоже есть противоположные:

Есть ноль (нейтральный элемент по сложению):

\[\begin 0 & =0+0\cdot i \\ z & =a+bi \\ z+0 & =\left( a+0 \right)+\left( b+0 \right)\cdot i= \\ & =a+bi=z \end\]

В общем, множество комплексных чисел — это абсолютно «нормальное» множество с понятной операцией сложения. Буквально через пару минут мы определим и умножение, но сначала давайте всё-таки запишем определение самого множества комплексных чисел.

Записывается это так:

Не пугайтесь, когда увидите подобную запись где-нибудь в учебнике алгебры. По сути, это краткая запись всего того, о чём мы говорили выше. Ничего нового мы здесь не узнали.

А вот что действительно представляет интерес — сейчас узнаем.:)

4. Геометрическая интерпретация комплексных чисел

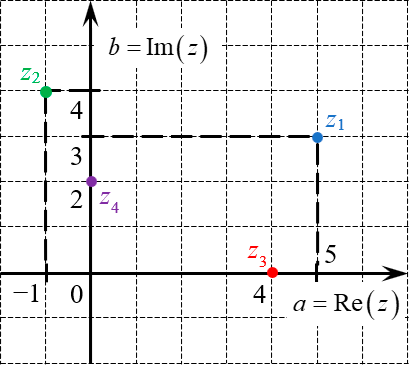
Такие упорядоченные пары удобно рассматривать как координаты точек. По горизонтали (ось абсцисс) мы будем отмечать действительную часть числа, а по вертикали (ось ординат) — мнимую.

Определение. Комплексная плоскость — декартова система координат, где по горизонтали отмечается действительная часть комплексного числа, а по вертикали — мнимая.

Рассмотрим несколько примеров. Отметим на комплексной плоскости числа:

4.1. Ещё раз о сложении и вычитании

Такое представление чисел — в виде точек на комплексной плоскости — называется геометрической интерпретацией. Числа в таком виде удобно складывать и вычитать. По сути, всё сводится к сложению обычных векторов.

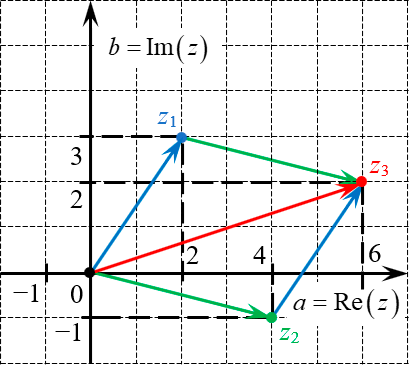
Допустим, мы хотим сложить два числа:

Отметим эти числа на комплексной плоскости, построим векторы из начала координат с концами в отмеченных точках, а затем просто сложим эти векторы (по правилу треугольника или параллелограмма — как пожелаете):

Координаты новой точки: (6; 2). Следовательно, сумма равна:

Аналогичный результат можно получить и алгебраически:

Как видим, алгебраические выкладки заняли гораздо меньше времени и места. Уже хотя бы потому что не потребовалось чертить систему координат.:)

Зачем же тогда нужна комплексная плоскость и геометрическая интерпретация? Всё встанет на свои места буквально через пару уроков, когда мы рассмотрим тригонометрическую форму записи комплексных чисел, а также будем извлекать из этих чисел корни.

А чтобы подготовиться к этим урокам, рассмотрим ещё два ключевых определения.

5. Комплексно-сопряжённые и модуль числа

Для начала вспомним школьную алгебру. Работа с многочленами, 7-й класс:

называется разностью квадратов и является одной из формул сокращённого умножения.

В математических классах с помощью сопряжённых искали обратные числа, чтобы затем решать сложные показательные и логарифмические уравнения:

Теперь настало время комплексных чисел. В них тоже можно ввести понятие сопряжённых.

5.1. Комплексно-сопряжённые

Комплексно-сопряжённые числа отмечаются чертой сверху.

Рассмотрим несколько примеров:

Видим, что комплексно-сопряжённое к «чисто мнимому» числу есть число, ему противоположное. А комплексно-сопряжённое к действительному числу есть само это число.

Зачем нужны комплексно-сопряжённые? Вспомним всё ту же формулу разности квадратов:

Итак, произведение числа на комплексно-сопряжённое даёт сумму квадратов действительной и мнимой части. Это ключевое свойство комплексно-сопряжённых, и оно позволяет нам рассмотреть следующее определение.

5.2. Модуль комплексного числа

Снова вспомним школьную алгебру. Модуль действительного числа определяют так:

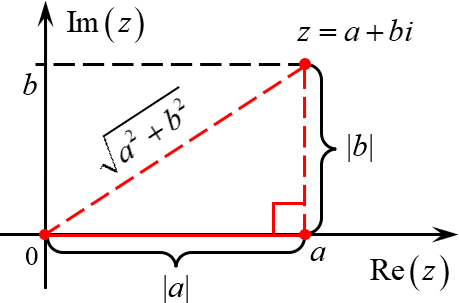
Ключевая идея: модуль числа — это всегда неотрицательная величина, равная расстоянию от точки, соответствующей этому числу, до начала отсчёта. Но всё это происходит на числовой прямой. На комплексной плоскости к делу подключается теорема Пифагора.

Вновь обратимся к геометрической интерпретации:

\[b=0\Rightarrow \left| z \right|=\sqrt<<^<2>>>\]

Получается, что на множестве комплексных чисел нельзя ввести привычные нам понятия «больше» или «меньше». Поскольку каждое число характеризуется двумя независимыми параметрами (действительной и мнимой частью), нет универсальной меры, нет отношения порядка.

Можно считать это фундаментальным законом природы. Когда мы держим в голове больше одного параметра, нет больше универсального критерия успеха:

Оценка одного и того же события будет меняться в зависимости от настроения и наших предпочтений.

Модуль числа нам пригодится в следующем уроке. А вот комплексно-сопряжённые мы будем применять уже сейчас.

6. Умножение и деление комплексных чисел

Комплексные числа можно не только складывать и вычитать, но даже умножать и делить друг на друга.

6.1. Умножение

С умножением ничего особенного.

\[\begin <_<1>>\cdot <_<2>> & =\left( a+bi \right)\left( c+di \right)= \\ & =ac+bc\cdot i+ad\cdot i+bd\cdot <^<2>>= \\ & =\left( ac-bd \right)+\left( ad+bc \right)\cdot i\end\]

Как видим, произведение комплексных чисел вновь даёт комплексное число.

Как и в случае со сложением, не нужно учить эти формулы наизусть. Лучше просто потренироваться и понять сам механизм:

Достаточно решить 10—15 таких примеров — и никакие специальные формулы и определения вам больше не понадобятся. То же самое и с делением.

6.2. Деление

Финальный бросок — попробуем разделить одно комплексное число на другое. Разумеется, делитель не должен быть нулём, иначе частное не определено.

Частное комплексных чисел вновь будет комплексным числом.

Саму формулу не нужно запоминать. Достаточно лишь отметить для себя, что мы умножили числитель и знаменатель дроби на комплексно-сопряжённое к знаменателю. Само деление можно выполнять напролом:

Тем не менее, даже после основательной тренировки умножение и особенно деление комплексных чисел остаётся трудоёмкой операцией, где можно допустить множество ошибок. Поэтому для таких операций (а также для кое-чего гораздо более серьёзного) математики придумали другую форму записи комплексных чисел — тригонометрическую. С ней мы и познакомимся на следующем уроке.:)

Источник