Для чего нужны обратные тригонометрические функции
Алгебра и начала математического анализа. 11 класс
Конспект урока
Алгебра и начала математического анализа, 11 класс
Урок №6. Обратные тригонометрические функции.
Перечень вопросов, рассматриваемых в теме
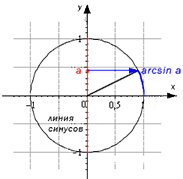
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ). Он имеет область определения 

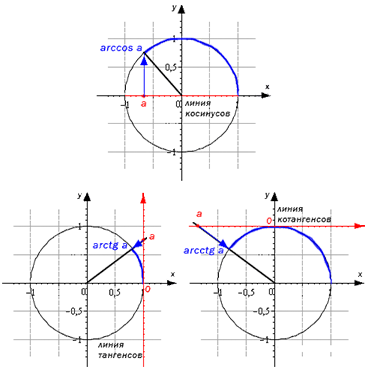
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ). Он имеет область определения 
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ). Он имеет область определения 

Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ). Он имеет область определения 
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Обратные тригонометрические функции решают задачу вычисления углов по известному значению тригонометрической функции. Например, косинус какого угла равен 


Объяснение нового материала
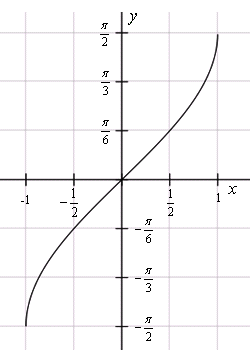
Рассмотрим свойства функции y=arcsin x и построим ее график.
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ).
Основные тригонометрические тождества, их формулировки и вывод
В этой статье мы разберем такие важные понятия в тригонометрии, как арксинус, арккосинус, арктангенс и арккотангенс. Мы можем найти значения чисел (углов), если знаем данные тригонометрических функций; это и есть та самая задача, что приводит нас к обратным функциям.
Ниже мы не только дадим определения основных понятий и общепринятые обозначения, но и приведем расчеты, из которых будет ясно, что они из себя представляют. В конце мы попробуем связать понятия арккотангенса, арктангенса, арккосинуса и арксинуса с понятием единичной окружности.
Основные определения
Арксинус и другие обратные функции как угол
Сформулируем основные определения.
Вышеуказанные определения можно сформулировать в более краткой и символической форме:
Если вы хотите более подробно изучить такой подход к определению обратных тригонометрических функций, рекомендуем вам учебник Кочеткова (ч.1, стр. 260-278)
Арксинус и другие обратные функции как число
В том случае, если в задаче речь идет, скажем, о синусе угла, то логично его арксинус также воспринимать как угол. Если нам нужно, например, вычислить косинус некоторого числа, то тут важно встать на другую точку зрения и рассмотреть обратные функции как числа. Исходя из второго подхода, можно немного переформулировать определения:
Такие формулировки типичны для большинства современных учебников по математике.
Объяснение обратных функций с позиции геометрии
Более наглядно представить обратные функции числа можно геометрически: ведь если это углы, их можно изобразить на чертеже. Это просто сделать, если вы еще не забыли базовые определения основных прямых функций.
Для этого нам понадобится уже знакомая нам единичная окружность. Ее дуги, связывающие между собой основные углы, и будут соответствовать величинам обратных функций.
Вывод: что такое аркфункции
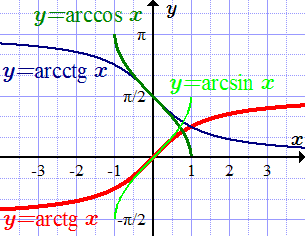
Обратные тригонометрические функции и их графики
Обратные тригонометрические функции — это арксинус, арккосинус, арктангенс и арккотангенс.
Сначала дадим определения.
Расскажем подробно об этих четырех новых для нас функциях — обратных тригонометрических.
Например, арифметический квадратный корень из числа а — такое неотрицательное число, квадрат которого равен а.
Логарифм числа b по основанию a — такое число с, что
Мы понимаем, для чего математикам пришлось «придумывать» новые функции. Например, решения уравнения — это и Мы не смогли бы записать их без специального символа арифметического квадратного корня.
Понятие логарифма оказалось необходимо, чтобы записать решения, например, такого уравнения: Решение этого уравнения — иррациональное число Это показатель степени, в которую надо возвести 2, чтобы получить 7.
Так же и с тригонометрическими уравнениями. Например, мы хотим решить уравнение
Ясно, что его решения соответствуют точкам на тригонометрическом круге, ордината которых равна И ясно, что это не табличное значение синуса. Как же записать решения?
Здесь не обойтись без новой функции, обозначающей угол, синус которого равен данному числу a. Да, все уже догадались. Это арксинус.
А вторая серия решений нашего уравнения — это
Подробнее о решении тригонометрических уравнений — здесь.
Повторим определение еще раз:
Мы готовы построить график функции
Как обычно, отмечаем значения х по горизонтальной оси, а значения у — по вертикальной.
Значит, областью определения функции y = arcsin x является отрезок
Заметим, что график функции y=arcsinx весь помещается в области, ограниченной линиями и
Как всегда при построении графика незнакомой функции, начнем с таблицы.
Строим график функции
1. Область определения
2. Область значений
Напомним, что графики взаимно обратных функций симметричны относительно прямой
Аналогично, определим функцию Только отрезок нам нужен такой, на котором каждому значению угла соответствует свое значение косинуса, а зная косинус, можно однозначно найти угол. Нам подойдет отрезок
Арккосинусом числа a называется число , такое, что
Легко запомнить: «арккосинусы живут сверху», и не просто сверху, а на отрезке
Обозначение: Область определения арккосинуса — отрезок Область значений — отрезок
Арккосинус не является ни чётной, ни нечётной функцией. Зато мы можем использовать следующее очевидное соотношение:
Построим график функции
Заполним таблицу, пользуясь определением арккосинуса.
Вот график арккосинуса:
1. Область определения
2. Область значений
Эта функция общего вида — она не является ни четной, ни нечетной.
5. Функции и являются взаимно обратными.
Следующие — арктангенс и арккотангенс.
Арктангенсом числа a называется число , такое, что
Дальше рассуждаем так же, как при построении графиков арксинуса и арккосинуса.
А что же будет при бесконечно больших значениях х? Другими словами, как ведет себя эта функция, если х стремится к плюс бесконечности?
Мы можем задать себе вопрос: для какого числа из интервала значение тангенса стремится к бесконечности? — Очевидно, это
А значит, при бесконечно больших значениях х график арктангенса приближается к горизонтальной асимптоте
Аналогично, если х стремится к минус бесконечности, график арктангенса приближается к горизонтальной асимптоте
На рисунке — график функции
1. Область определения
2. Область значений
3. Функция нечетная.
4. Функция является строго возрастающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными — конечно, когда функция рассматривается на промежутке
Аналогично, определим функцию арккотангенс и построим ее график.
Арккотангенсом числа a называется число , такое, что
1. Область определения
2. Область значений
4. Функция является строго убывающей.
5. Прямые и — горизонтальные асимптоты данной функции.
6. Функции и являются взаимно обратными, если рассматривать на промежутке
Обратные тригонометрические функции, их графики и формулы
Определение обратных тригонометрических функций
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
Графики обратных тригонометрических функций
y = arcsin x 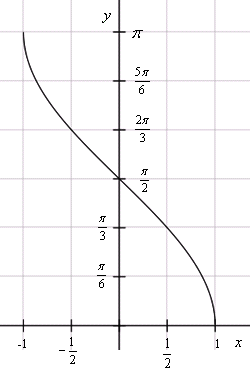
y = arccos x 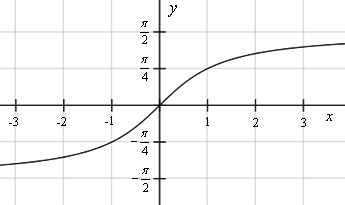
y = arctg x 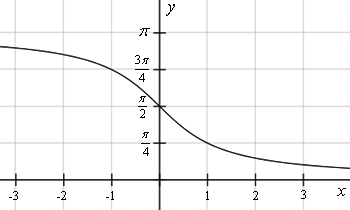
y = arcctg x
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin x ) = x при
sin(arcsin x ) = x
arccos(cos x ) = x при
cos(arccos x ) = x
arctg(tg x ) = x при
tg(arctg x ) = x
arcctg(ctg x ) = x при
ctg(arcctg x ) = x
Формулы, связывающие обратные тригонометрические функции
Формулы суммы и разности
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Обратные тригонометрические функции, их графики и формулы
Определение обратных тригонометрических функций
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
Графики обратных тригонометрических функций

y = arcsin x 
y = arccos x 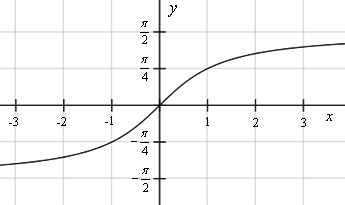
y = arctg x 
y = arcctg x
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin x ) = x при
sin(arcsin x ) = x
arccos(cos x ) = x при
cos(arccos x ) = x
arctg(tg x ) = x при
tg(arctg x ) = x
arcctg(ctg x ) = x при
ctg(arcctg x ) = x
Формулы, связывающие обратные тригонометрические функции
Формулы суммы и разности
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.