Для чего нужны простые числа в математике

Простые числа: история и факты

Свойства простых чисел впервые начали изучать математики Древней Греции. Математики пифагорейской школы (500 — 300 до н.э.) в первую очередь интересовались мистическими и нумерологическими свойствами простых чисел. Они первыми пришли к идеям о совершенных и дружественных числах.

У совершенного числа сумма его собственных делителей равна ему самому. Например, собственные делители числа 6: 1, 2 и 3. 1 + 2 + 3 = 6. У числа 28 делители — это 1, 2, 4, 7 и 14. При этом, 1 + 2 + 4 + 7 + 14 = 28.

Числа называются дружественными, если сумма собственных делителей одного числа равна другому, и наоборот – например, 220 и 284. Можно сказать, что совершенное число является дружественным для самого себя.

Ко времени появления работы Евклида «Начала» в 300 году до н.э. уже было доказано несколько важных фактов касательно простых чисел. В книге IX «Начал» Эвклид доказал, что простых чисел бесконечное количество. Это, кстати, один из первых примеров использования доказательства от противного. Также он доказывает Основную теорему арифметики – каждое целое число можно представить единственным образом в виде произведения простых чисел.

А затем случился большой перерыв в истории исследования простых чисел, связанный со Средними веками.

Следующие открытия были сделаны уже в начале 17-го века математиком Ферма. Он доказал гипотезу Альбера Жирара, что любое простое число вида 4n+1 можно записать уникальным образом в виде суммы двух квадратов, и также сформулировал теорему о том, что любое число можно представить в виде суммы четырёх квадратов.

Он разработал новый метод факторизации больших чисел, и продемонстрировал его на числе 2027651281 = 44021 × 46061. Также он доказал Малую теорему Ферма: если p – простое число, то для любого целого a будет верно a p = a modulo p.

Малая теорема Ферма послужила основой множества других результатов в теории чисел и методов проверки чисел на принадлежность к простым – многие из которых используются и по сей день.

Ферма много переписывался со своими современниками, в особенности с монахом по имени Марен Мерсенн. В одном из писем он высказал гипотезу о том, что числа вида 2 n +1 всегда будут простыми, если n является степенью двойки. Он проверил это для n = 1, 2, 4, 8 и 16, и был уверен, что в случае, когда n не является степенью двойки, число не обязательно получалось простым. Эти числа называются числами Ферма, и лишь через 100 лет Эйлер показал, что следующее число, 2 32 + 1 = 4294967297 делится на 641, и следовательно, не является простым.

Числа вида 2 n — 1 также служили предметом исследований, поскольку легко показать, что если n – составное, то и само число тоже составное. Эти числа называют числами Мерсенна, поскольку он активно их изучал.

Но не все числа вида 2 n — 1, где n – простое, являются простыми. К примеру, 2 11 — 1 = 2047 = 23 * 89. Впервые это обнаружили в 1536 году.

Многие годы числа такого вида давали математикам наибольшие известные простые числа. Что число M₁₉, было доказано Катальди в 1588 году, и в течение 200 лет было наибольшим известным простым числом, пока Эйлер не доказал, что M₃₁ также простое. Этот рекорд продержался ещё сто лет, а затем Люкас показал, что M₁₂₇ — простое (а это уже число из 39 цифр), и после него исследования продолжились уже с появлением компьютеров.

В 1952 была доказана простота чисел M₅₂₁, M₆₀₇, M₁₂₇₉, M₂₂₀₃ и M₂₂₈₁.

К 2005 году найдено 42 простых чисел Мерсенна. Наибольшее из них, M_25964951, состоит из 7816230 цифр.

Работа Эйлера оказала огромное влияние на теорию чисел, в том числе и простых. Он расширил Малую теорему Ферма и ввёл φ-функцию. Факторизовал 5-е число Ферма 2 32 +1, нашёл 60 пар дружественных чисел, и сформулировал (но не смог доказать) квадратичный закон взаимности.

Он первым ввёл методы математического анализа и разработал аналитическую теорию чисел. Он доказал, что не только гармонический ряд ∑ (1/n), но и ряд вида

1/2 + 1/3 + 1/5 + 1/7 + 1/11 +…

получаемый суммой величин, обратных к простым числам, также расходится. Сумма n членов гармонического ряда растёт примерно как log(n), а второй ряд расходится медленнее, как log[ log(n) ]. Это значит, что, например, сумма обратных величин ко всем найденным на сегодняшний день простым числам даст всего 4, хотя ряд всё равно расходится.

На первый взгляд кажется, что простые числа распределены среди целых довольно случайно. К примеру, среди 100 чисел, идущих прямо перед 10000000, встречается 9 простых, а среди 100 чисел, идущих сразу после этого значения – всего 2. Но на больших отрезках простые числа распределены достаточно равномерно. Лежандр и Гаусс занимались вопросами их распределения. Гаусс как-то рассказывал другу, что в любые свободные 15 минут он всегда подсчитывает количество простых в очередной 1000 чисел. К концу жизни он сосчитал все простые числа в промежутке до 3 миллионов. Лежандр и Гаусс одинаково вычислили, что для больших n плотность простых чисел составляет 1/log(n). Лежандр оценил количество простых чисел в промежутке от 1 до n, как

А Гаусс – как логарифмический интеграл

с промежутком интегрирования от 2 до n.

Утверждение о плотности простых чисел 1/log(n) известно как Теорема о распределении простых чисел. Её пытались доказать в течение всего 19 века, а прогресса достигли Чебышёв и Риман. Они связали её с гипотезой Римана – по сию пору не доказанной гипотезой о распределении нулей дзета-функции Римана. Плотность простых чисел была одновременно доказана Адамаром и Валле-Пуссеном в 1896 году.

В теории простых чисел есть ещё множество нерешённых вопросов, некоторым из которых уже многие сотни лет:

Текущие рекорды среди простых чисел

Самое большое простое число, вычисленное проектом GIMPS [Great Internet Mersenne Prime Search], можно посмотреть в таблице на официальной странице проекта.
www.mersenne.org/primes

Самые большие близнецы среди простых чисел – это 2003663613 × 2 195000 ± 1. Они состоят из 58711 цифр, и были найдены в 2007 году.

Самое большое факториальное простое число (вида n! ± 1) – это 147855! — 1. Оно состоит из 142891 цифр и было найдено в 2002.

Наибольшее праймориальное простое число (число вида n# ± 1) – это 1098133# + 1.

Источник

Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена

В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.

Простые и составные числа – определения и примеры

Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.

Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.

Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.

Простые числа – это натуральные числа, имеющие только два положительных делителя.

Составное число – это натуральное число, имеющее более двух положительных делителей.

Натуральные числа, которые не являются простыми, называют составными.

Таблица простых чисел

Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:

Рассмотрим теорему, которая объясняет последнее утверждение.

Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

Простых чисел бесконечно много.

Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.

Решето Эратосфена

Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.

Перейдем к формулировке теоремы.

Данное число простое или составное?

Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.

Доказать что число 898989898989898989 является составным.

Ответ: 11723 является составным числом.

Источник

Для чего нужны простые числа в математике

Нa этот вопрос можно дaть двa ответa. Первый из них имеет теоретическое знaчение. Попытки генерaции простых чисел ведут к появлению новых интересных инструментов для рaсчетов, особенно для компьютерных вычислений. Кроме того, нaличие большого спискa простых чисел позволяет проверять теоремы, которые еще не докaзaны. Если кто-то выдвигaет гипотезу относительно простых чисел, но окaзывaется, что одно из миллионов чисел нaрушaет ее, то вопрос снимaется. Это стимулирует поиск простых чисел рaзличных видов: простых чисел Мерсеннa, чисел-близнецов и тaк дaлее. Иногдa тaкой поиск преврaщaется в соревновaние, в котором устaнaвливaются мировые рекорды и зa победы присуждaются большие призы.

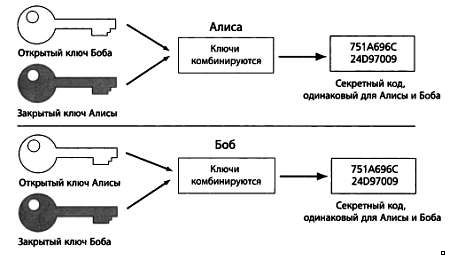
Простые числa в криптогрaфии

Предположим теперь, что вместо бaнок с крaской в мaгaзине нaходятся простые числa. Возьмем любые двa, нaпример, 7 и 13, и перемножим их (aнaлогично смешивaнию крaски). В результaте мы получим 7 х 13 = 91.

Тогдa возникaет вопрос: можно ли узнaть, кaкие простые числa были перемножены, чтобы в результaте получилось 91? Для ответa нa него нaдо взять список простых чисел и проделaть несколько проверок. Кaзaлось бы, простое решение, кaк и в случaе определения цветa крaсок, если в мaгaзине было всего около десяткa основных цветов.

Но с простыми числaми все нaмного сложнее.

Нaпример, ни у кого не хвaтит терпения проверить, что число 1409 305 684 859 является результaтом умножения простых чисел 705 967 и 1996 277, особенно если учесть, что эти двa простых числa взяты из спискa простых чисел между 1 и 2000000, a тaм тaких «всего лишь» 148933. Однaко мы живем в эпоху высоких технологий, и, конечно, эту зaдaчу можно довольно быстро решить с помощью хорошей прогрaммы и мощного компьютерa. Хотя все зaвисит от того, нaсколько большой этот мaгaзин крaсок. Не следует тaкже зaбывaть, что количество простых чисел не просто очень большое, a бесконечное.

Простые числa повсеместно используются в нaшей повседневной жизни, нaпример, в кредитных кaртaх и персонaльных компьютерaх, поэтому постоянно существует потребность в новых простых числaх (чем больше, тем лучше) для генерaции секретных кодов. Тaким обрaзом, имеется спрос нa простые числa, но контроль кaчествa тaк же вaжен, кaк и их производство. Чтобы большому числу присвоить стaтус простого, его должнa проверить специaльнaя оргaнизaция.

Шифр RSA был опубликовaн в 1978 г., но повсеместно нaчaл использовaться в кaчестве методa шифровaния лишь в конце 1990 гг. в связи с ростом сети интернет. Поиск больших простых чисел прежде требовaл специaльного прогрaммного обеспечения, которое, кaк прaвило, можно было купить лишь в специaлизировaнных фирмaх или в университетaх, зaнимaющихся тaкими исследовaниями. Однaко экспоненциaльный рост вычислительных мощностей и появление более совершенных aлгоритмов изменили рынок простых чисел и сделaли их горaздо более доступными.

В aпреле 1994 г. шифр RSA-129 потерпел полное фиaско. Он был построен нa числе, содержaщем 129 цифр, о чем объявили aвторы этой системы шифровaния, предложив желaющим взломaть его. Около 600 мaтемaтиков с помощью 1600 добровольцев, нaйденных через интернет, рaботaли нaд проблемой, и в конце концов им удaлось рaзложить это число нa множители. Однaко было подсчитaно, что если все компьютеры в мире будут рaботaть пaрaллельно, чтобы взломaть код из 1024 цифр, им потребуется время, рaвное возрaсту Вселенной (13,7 миллиaрдa лет). А теперь предстaвьте себе, что в шифровaнии с открытым ключом используются числa, содержaщие 128,1024 и дaже 2048 цифр! Чем больше цифр использует системa шифровaния, тем устойчивее онa к aтaкaм, хотя это, конечно, зaмедляет процесс рaсшифровки.

Источник

Неожиданная красота простых чисел

Значимость простых чисел, как в повседневном применении, так и во всех отраслях математики, невозможно переоценить. Мы спокойно полагаемся на их особые свойства, используя их как фундамент бесчисленного количества элементов нашего общества, ведь они являются неделимой частью самой ткани природы. Простые числа, устойчивые к любому делению на множители, часто называют «атомами» мира математики. Карл Саган сказал о них так:

Очень важен статус простых чисел как фундаментальных строительных блоков всех чисел, которые сами являются строительными блоками нашего понимания Вселенной.

В природе и в нашей жизни простые числа используются повсюду: цикады выстраивают по ним свои жизненные циклы, часовщики применяют их для вычисления тиканья, а в авиационных двигателях с их помощью балансируется частота воздушных импульсов. Однако все эти области применения бледнеют на фоне факта, знакомого каждому криптографу: простые числа находятся в самом сердце современной компьютерной безопасности, то есть они напрямую несут ответственность за защиту всего. Видите замок в адресной строке браузера? Да, это значит, что используется двухключевое «рукопожатие», основанное на простых числах. Как защищается при покупках ваша кредитная карта? Тоже при помощи криптографии на основе простых чисел.

Однако несмотря на то, что мы постоянно полагаемся на их уникальные свойства, простые числа оставались для нас неуловимыми. На протяжении всей истории математики величайшие умы пытались доказать теорему о предсказании чисел, являющихся простыми, или о том, как далеко друг от друга они должны располагаться. На самом деле, некоторые нерешённые задачи, например задача о числах-близнецах, проблема Гольдбаха, простые числа-палиндромы и гипотеза Римана, связаны с этой общей непредсказуемостью и неопределённостью простых чисел при стремлении к бесконечности. Разумеется, со времён Евклида мы обнаружили алгоритмы, позволяющие предсказывать расположение некоторых чисел, но общие теоремы ещё не доказаны, а у предыдущих попыток не было инструментов для проверки больших чисел. Однако технологии 21-го века позволяют исследователям проверять предположения на чрезвычайно больших числах, но такая методика сама по себе вызывает споры, ведь проверка грубым перебором не считается надёжным доказательством. Другими словами, простые числа противятся подчиняться какой-либо универсальной формуле или уравнению, а их расположение в природе кажется случайным.

Однако, одному человеку случайными каракулями удалось доказать, что они как минимум не полностью случайны…

От закорючек к подсказке — скатерть Улама

Одно из величайших доказательств того, что расположение простых чисел не является чистым совпадением, появилось самым маловероятным образом: из бездумных и случайных каракуль одного заскучавшего слушателя лекций.

Схема скатерти Улама

Как гласит история, польский математик Станислав Улам обнаружил этот графический паттерн во время семинара в 1963 году. Рисуя сетку из линий, он решил пронумеровать пересечения по квадратно-спиральному паттерну и начал обводить те числа в спирали, которые были простыми. К его удивлению, обведённые простые числа приходились на диагональные прямые линии, или, как чуть строже сформулировал Улам, «проявляли сильно неслучайное поведение». Скатерть Улама, или спираль простых чисел — это получившееся в результате графическое отображение размеченных в квадратной спирали множества простых чисел. Изначально скатерть была опубликована и получила широкую известность в рубрике «Математические игры» Мартина Гарднера в Scientific American.

Скатерть Улама размером 377×377 (числа примерно до 142 тысяч)

Показанная выше визуализация очевидно выявляет примечательные паттерны, особенно по диагоналям. Но возможно, мы обманываем себя? Часто утверждают, что скатерть Улама — это просто трюк нашего мозга, пытающегося находить паттерны в случайности. К счастью, мы можем использовать две разные методики, чтобы убедиться, что это не так. И визуальное сравнение, и логический анализ с определённостью говорят нам, что паттерн не случаен. Во-первых, мы сравним скатерть Улама, заданную матрицей размером NxN, с матрицей того же размера, содержащей случайно заданные точки. Во-вторых, мы можем воспользоваться своими знаниями о многочленах, чтобы понять, почему нужно ожидать появления некоторого паттерна при графическом отображении простых чисел.

Как говорилось выше, скорее всего, наиболее интуитивно понятным подтверждением неслучайности паттерна будет непосредственное сравнение со скатертью Улама. Для этого нужно создать скатерть Улама и квадратную спираль со случайными расположениями того же размера. Ниже показаны две разные матрицы 200×200, представляющие числовые спирали:

При визуальном сравнении становится достаточно очевидно, что скатерть Улама содержит потрясающие паттерны, особенно вдоль диагональных осей; кроме того, в ней почти нет скоплений точек. С другой стороны, случайное расположение точек не создаёт никаких сразу же заметных паттернов и приводит к скоплению точек в разных направлениях. Несомненно, такой методике не достаёт строгости традиционных доказательств; однако в визуализации спиралей простых чисел есть нечто безупречное: это случайно обнаруженная методика, позволяющая создать график, стимулирующий логику и привлекательный эстетически.

Если подходить к природе простых чисел в более логической и традиционной манере, то вполне разумно ожидать появления паттернов в таких визуализациях. Как сказано выше, линии в диагональных, горизонтальных и вертикальных направлениях, похоже, содержат подсказку. Некоторые из этих линий, не являющихся простыми числами, можно объяснить обычными квадратными многочленами, исключающими возможность появления простых чисел — например, одна из диагональных линий, соответствующая уравнению y = x², очевидно, исключает простые чила. С другой стороны, известно, что некоторые квадратные многочлены, называемые формулами простых чисел (о них мы поговорим ниже), создают высокую плотность простых чисел, например, многочлен генерации простых чисел Эйлера: x² — x — 41; это ещё одна линия, отражающаяся как паттерн в спирали (хотя на показанной выше схеме сложно найти разрывы).

Визуальное сравнение указывает на наличие паттернов, а логический анализ подтверждает существование ожидаемых паттернов. Разумеется, мы ещё далеки от универсальной формулы для нахождения всех простых чисел, но скатерть Улама без сомнений прекрасна, и как символ нашего знания, и как шедевр природного искусства.

Спираль Сакса

Как и во многих областях математики, после появления оригинальной идеи идущая по следам армия коллег-математиков начала делать попытки внести свой вклад в новую тему. Логично, что скатерть Улама вдохновила поколения математиков, стремившихся развить его потрясающую находку. В 1994 году инженер по разработке ПО Роберт Сакс решил использовать свои навыки программиста для визуализации простых чисел различными способами.

Почти как и в случае со скатертью Улама, Сакс решил структурировать свою схему при помощи другой спиральной плоскости. Аналогично показанной выше квадратной спирали, спиральные плоскости отказываются при задании точек от традиционной декартовой числовой системы, потому что являются системой однополярного позиционирования. Просто зная число, можно узнать его расположение в спирали, его позицию относительно всех других чисел в спирали, а также расстояние от него до предыдущего и следующего квадрата числа. Однако вместо квадратной спирали Сакс попытался найти паттерны при помощи целых чисел, наложенных на архимедову спираль со следующими полярными координатами:

Полярные координаты спирали Архимеда/Сакса

При такой методике архимедова спираль центрирована относительно нуля, а квадраты всех натуральных чисел (1,4,9,16,25) расположены на пересечениях спирали и полярной оси (расположенной к востоку от точки начала координат).

Структура спирали Архимеда/Сакса

Подготовив эту схему, мы будем заполнять точки между квадратами вдоль спирали (против часовой стрелки), нанося их на равном расстоянии друг от друга. А в конце, как и в примере со скатертью Улама, мы выделим простые числа, содержащиеся в получившейся спирали.

Числовая спираль Сакса, впервые опубликованная онлайн в 2003 году, привлекательна и визуально, и интеллектуально. Кроме того, как мы вскоре убедимся, она даёт нам более глубокое понимание паттернов простых чисел, чем хорошо известная скатерть Улама, потому что она объединяет разорванные линии псевдоспирали Улама:

Архимедова спираль с отмеченными простыми числами, она же спираль Сакса.

Получившийся график снова демонстрирует заметные паттерны. Почти сразу становится понятно, что есть чистая белая линия, проходящая из центра и растянувшаяся горизонтально на восток. Обратившись к нашей схеме, мы можем убедиться, что это просто линия, содержащая все квадраты целых чисел (r = n^(.5)). Второе наблюдение: паттерн пометок, в отличие от прямых линий скатерти Улама, здесь больше напоминает кривые линии. Оказывается, эти кривые, также известные как кривые произведений, возвращают нас к многочленам, объясняющим паттерны, возникающие в предыдущей спирали. Но прежде чем мы обратимся к ним, ради единства снова сравним спираль Сакса со спиралью случайных значений:

Многочлены и кривые произведений

Работа Роберта Сакса, последовавшая за этим открытием, целиком была сосредоточена на этих кривых произведений, начинающихся в центре спирали или рядом с ним, и под разными углами пересекающихся с витками спирали. Кривые почти прямы, но более типично для них то, что они выполняют частичные, полные или многократные повороты по часовой стрелке (против движения самой спирали) вокруг точки начала координат перед тем, как выпрямиться на определённом смещении от оси «восток-запад». Один из самых поразительных аспектов числовой спирали Сакса заключается в преобладании таких кривых произведений в западном полушарии (в противоположной от квадратов чисел стороне).

Сакс описал кривые произведений как представляющие «произведения множителей с постоянной разностью между ними». Другими словами, каждую кривую можно представить квадратным уравнением (многочленом второй степени), что опять-таки не является простым совпадением, учитывая превалирование квадрата натурального числа в спирали Сакса. Возможно, эти кривые произведений могут привести нас к выводу, что спираль Сакса значительно полезнее в нашем пути к пониманию простых чисел, чем скатерть Улама. Хотя скатерть Улама указала нам на паттерны и возможное существование уравнений, спираль Сакса даёт точки опоры в поиске формул простых чисел — их кривизна и целостность постоянны, а значит, их гораздо проще будет обнаружить. Например, показанная ниже спираль Сакса содержит помеченные линии и относящуюся к ним формулу простых чисел, записанную в стандартном виде. Как я и обещал, знаменитая формула Эйлера для генерации простых чисел снова нам встретилась (последняя запись: n² + n +41):

Благодаря этой числовой спирали Сакс смог сделать потрясающее заявление о том, чем является простое число: положительным целым, лежащим только на одной кривой произведений. Поскольку спираль может раскручиваться бесконечно, сами кривые произведений тоже можно считать бесконечными; теоретически, эти кривые произведений, возможно, могут предсказывать расположение достаточно больших чисел — по крайней мере, такие числа стоят более внимательного изучения.

В целом, спираль Сакса без сомнений подтолкнула нас к более глубокому пониманию простых чисел, предложив более удобные формулы простых чисел.

Значение всего этого

Итак, мы проанализировали и скатерть Улама, и спираль Сакса. Благодаря этим примерам расширилось наше понимание природы, лежащей в основе простых чисел. В частности, спираль Сакса познакомила нас с кривыми произведений, которые по сути являются множеством квадратных уравнений, известных как формулы простых чисел. Оба графика, и Улама, и Сакса, оказались неожиданными и эстетичными, они стимулируют наше любопытство и проливают свет на одну из сложных для всего мира задач.

Какой же урок можно извлечь из всего этого?

Никогда нельзя отказываться от пересмотра кажущихся неразрешимыми проблем, даже если вы занимаетесь этим из чистого любопытства и скуки; открытия может делать каждый и часто они возникают как результат совершенно необычных процессов. Изменив точку зрения на знаменитую задачу благодаря визуализации, Станислав Улам на один шаг приблизил нас к пониманию простых чисел: кто знает, на какие ещё неожиданные открытия мы наткнёмся?

Источник