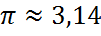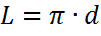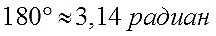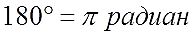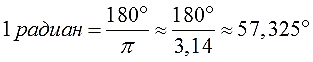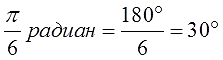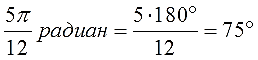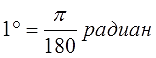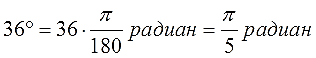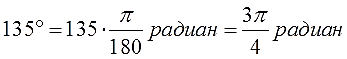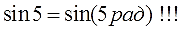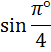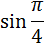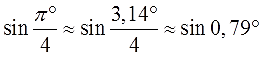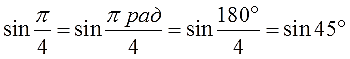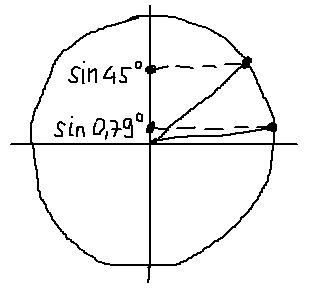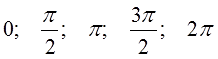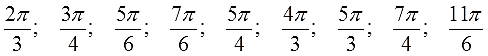Для чего нужны радианы
Радиан
Радиа́н (русское обозначение: рад, международное: rad; от лат. radius — луч, радиус) — основная единица измерения плоских углов в современной математике и физике. Радиан определяется как угловая величина дуги, длина которой равна её радиусу. Таким образом, величина полного угла равна 2 π радиан.
Так как величина угла, выраженная в радианах, равна отношению длины дуги окружности к длине её радиуса, радиан — величина безразмерная. Поэтому обозначение радиана (рад) часто опускается.
Содержание
Связь радиана с другими единицами
Соотношение радиана с другими единицами измерения углов описывается формулой:
Очевидно, 180° = π радиан. Отсюда вытекает тривиальная формула пересчёта из градусов, минут и секунд в радианы и наоборот.
α [рад] = α [°] × ( π / 180); α [°] = α [рад] × (180 / π ),
где α [рад] — угол в радианах, α [°] — угол в градусах
1 рад ≈ 57,295779513° ≈ 57°17′44,806″ ≈ 206265″.
Радианная мера в математическом анализе
При рассмотрении тригонометрических функций в математическом анализе всегда считается, что аргумент выражен в радианах, что упрощает запись.
При малых углах синус и тангенс угла, выраженного в радианах, приблизительно равны самому углу, что удобно при приближённых вычислениях:
Косинус малого угла, выраженного в радианах, приближённо равен:
Радиан в физике
Кратные и дольные единицы
Десятичные кратные и дольные единицы образуются с помощью стандартных приставок СИ, однако используются редко. Так, в миллирадианах, микрорадианах и нанорадианах измеряется угловое разрешение в астрономии. В кратных единицах (килорадианах и т. д.) измеряется набег угловой фазы. Сокращённое обозначение (рад, rad) основной и производных единиц не следует путать с устаревшей единицей измерения поглощённой дозы ионизирующего излучения — рад.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 10 1 рад | декарадиан | дарад | darad | 10 −1 рад | децирадиан | драд | drad |
| 10 2 рад | гекторадиан | град | hrad | 10 −2 рад | сантирадиан | срад | crad |
| 10 3 рад | килорадиан | крад | krad | 10 −3 рад | миллирадиан | мрад | mrad |
| 10 6 рад | мегарадиан | Мрад | Mrad | 10 −6 рад | микрорадиан | мкрад | µrad |
| 10 9 рад | гигарадиан | Град | Grad | 10 −9 рад | нанорадиан | нрад | nrad |
| 10 12 рад | терарадиан | Трад | Trad | 10 −12 рад | пикорадиан | прад | prad |
| 10 15 рад | петарадиан | Прад | Prad | 10 −15 рад | фемторадиан | фрад | frad |
| 10 18 рад | эксарадиан | Эрад | Erad | 10 −18 рад | атторадиан | арад | arad |
| 10 21 рад | зеттарадиан | Зрад | Zrad | 10 −21 рад | зепторадиан | зрад | zrad |
| 10 24 рад | йоттарадиан | Ирад | Yrad | 10 −24 рад | йокторадиан | ирад | yrad |
| применять не рекомендуется не применяются или редко применяются на практике | |||||||
Примечания
См. также
Полезное
Смотреть что такое «Радиан» в других словарях:
РАДИАН — РАДИАН, угол, образованный пересечением двух радиусов из центра ОКРУЖНОСТИ, при этом длина дуги, ограниченной этими радиусами, равна длине радиуса. Таким образом радиан единица измерения УГЛА, приблизительно равный 57,296°, а углу 360°… … Научно-технический энциклопедический словарь
РАДИАН — Лапландский бог, берущий, по их верованию, души умерших к себе на небо. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. радиан (лат. radius луч, радиус) мат. единица измерения плоских углов, употребляемая в… … Словарь иностранных слов русского языка
РАДИАН — (от лат. radius луч, радиус) (рад, rad), единица плоского угла; 1 рад равен углу между двумя радиусами окружности, длина дуги между к рыми равна радиусу. 1 рад=57°17 44,8 »3,44•103 угл. минут»2,06•105 угл. секунд»63,7g (см. ГРАД). Физический… … Физическая энциклопедия
радиан — а, м. radian m., нем. Radian <лат. лат. radius луч. Угол, соответствующий дуге, длина которой равна ее радиусу. БАС 1. Лекс. Гранат: радиан; СИС 1937: радиа/н … Исторический словарь галлицизмов русского языка
РАДИАН — РАДИАН, радиана, муж. (от лат. radius луч) (мат.). Единица измерения углов, представляющая собою угол, у которого дуга равна радиусу окружности. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
радиан — сущ., кол во синонимов: 3 • единица (830) • рад (7) • угол (27) Словарь синонимов ASIS. В.Н. Тришин … Словарь синонимов
радиан — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN radian … Справочник технического переводчика
Что такое один градус? Что такое один радиан? Перевод радианов в градусы и обратно.
В прошлый раз мы с вами ответили на первый вопрос, касаемый работы с углами. А именно — как отсчитываются углы. Рассмотрели положительные и отрицательные углы, а также углы, большие 360 градусов. И на круге углы порисовали.)
В этом же уроке настал черёд ответить на второй вопрос, связанный с измерением углов. Здесь мы разберёмся с загадочными радианами и особенно — с пресловутым числом «пи», которое будет мозолить нам глаза на протяжении всего дальнейшего изучения тригонометрии. Поймём, что это за число, откуда оно берётся и как с ним работать. И задания порешаем, само собой. Стандартные и не очень…)
Разберёмся? Ну сколько же можно бояться числа «пи», в конце-то концов!)
Итак, в чём же измеряются углы в математике? Начнём с привычного и знакомого. С градусов.
Что такое один градус? Градусная мера угла.
К градусам вы уже попривыкли. Геометрию изучаете, да и в жизни постоянно сталкиваетесь. Например, «повернул на 90 градусов».) Короче, градус — штука простая и понятная.
Вы и вправду так думаете? Тогда сможете сказать мне, что такое градус? Нет, гуглить и потрошить Википедию не надо. Ну как, слабо с ходу? Вот так-то…
Начнём издалека. С древнейших времён. А именно — с двух очагов древних цивилизаций Вавилона и Египта.)
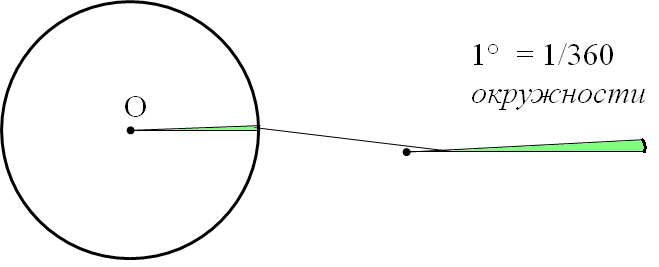
Градус — это 1/360 часть окружности. И всё!
Придумали градусы в Древнем Вавилоне.) Как? Очень просто! Просто взяли да разбили окружность на 360 равных кусочков. Почему именно на 360? А не на 100 или на 1000? Вроде бы, число 100 поровнее, чем 360… Вопрос хороший.
Основная версия — астрономическая. Ведь число 360 очень близко к числу дней в году! А для наблюдений за Солнцем, Луной и звёздами это было оч-чень удобно.)
Кроме того, в астрономии (а также строительстве, землемерии и прочих смежных областях) очень удобно делить окружность на равные части. А теперь давайте прикинем чисто математически, на какие числа делится нацело 100 и на какие — 360? И в каком из вариантов этих делителей нацело больше? А людям такое деление очень удобно, да…)
Что такое число «пи»? Как оно возникло?
А теперь переместимся из Древнего Вавилона в Древний Египет. Примерно в то же самое время там разгадывали другую загадку. Не менее интересную, чем вопрос, на сколько частей бить окружность. А именно — во сколько раз длина окружности больше её диаметра? Или по-другому: чему равна длина окружности с диаметром, равным единице?
И так измеряли и сяк… Каждый раз получалось чуть-чуть больше трёх. Но как-то коряво получалось, неровно…
Но они, египтяне, ни в чём не виноваты. После них математики всех мастей продолжали мучиться аж до 18 века! Пока в 1767 году окончательно не доказали, что, как бы мелко ни нарезать окружность на равные кусочки, из таких кусочков сложить точно длину диаметра нельзя. Принципиально нельзя. Только лишь примерно.
Нет, конечно же, во сколько раз длина окружности больше её диаметра установили давным-давно. Но, опять же, примерно… В 3,141592653… раза.
Это число — и есть число «пи» собственной персоной.) Да уж… Корявое так корявое… После запятой — бесконечное число цифр безо всякого порядка, безо всякой логики. В математике такие числа называются иррациональными. И на сегодняшний день доказательство факта иррациональности числа «пи» занимает аж десять (!) лекций на 4-м курсе мехмата МГУ… Этот факт, кстати, и означает, что из одинаковых кусочков окружности её диаметр точно не сложить. Никак. И никогда…
Конечно, рациональные приближения числа «пи» известны людям ещё со времён Архимеда. Например:
22/7 = 3,14285714…
377/120 = 3,14166667…
355/113 = 3,14159292…
Сейчас, в век суперкомпьютеров, погоня за десятичными знаками числа «пи» не стихает, и на сегодняшний день человечеству известно уже два квадриллиона (!) знаков этого числа…
Но нам для практического применения такая сверхточность совершенно не требуется. Чаще всего достаточно запомнить всего лишь две цифры после запятой.
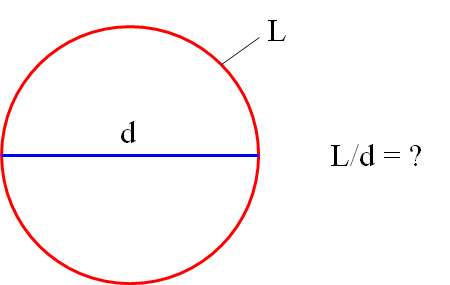
Вот и всё. Раз уж нам ясно, что длина окружности больше её диаметра в «пи» раз, то можно записать (и запомнить) точную формулу для длины окружности:
Здесь L — длина окружности, а d — её диаметр.
В геометрии всяко пригодится.)
Для общего развития скажу, что число «пи» сидит не только в геометрии или тригонометрии. Оно возникает в самых различных разделах высшей математики. В интегралах, например. Или в теории вероятностей. Или в теории комплексных чисел, а также рядов. Само по себе возникает, хотим мы того или нет… Поступите в ВУЗ — убедитесь лично.)
Ну а теперь снова вернёмся к старым добрым градусам. Как мы помним, один градус — это 1/360 часть окружности. С исторической и практической точек зрения людям такое деление на 360 равных частей оказалось очень даже удобно, но…
Как выяснилось гораздо позже Древнего Вавилона, градусы удобны далеко не всем. Например, высшей математике они ой как неудобны! Высшая математика — дама серьёзная. По законам природы устроена. И она справедливо заявляет: «Сегодня вы на 360 частей круг разбили, завтра — на 100 разобьёте, послезавтра — на 250… А мне что делать? Каждый раз под ваши хотелки подстраиваться?»
Против природы не попрёшь… Пришлось прислушаться и уступить. И ввести новую меру угла, не зависящую от наших хотелок. )
Итак, знакомьтесь — радиан!
Что такое один радиан? Радианная мера угла.
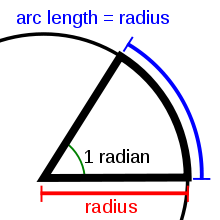
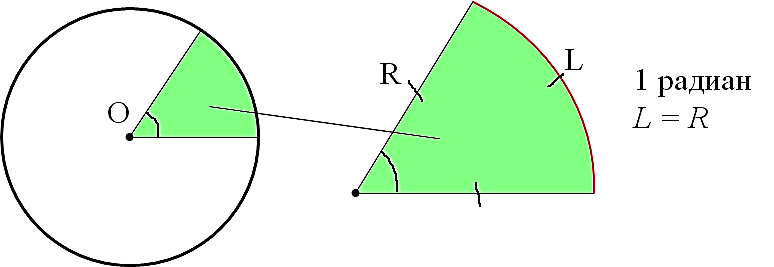
В основе определения радиана — та же самая окружность. Угол в 1 радиан — это угол, который отсекает от окружности дугу, длина которой (L) равна радиусу окружности (R). И всё!
Причём величина угла в один радиан не зависит от радиуса окружности! Никак. Можно нарисовать очень большую окружность, можно очень маленькую. Но угол, отсекающий от окружности дугу, равную радиусу, никогда не изменит своей величины и будет составлять ровно один радиан. Всегда. Это важно.)
Запоминаем:
Угол в один радиан — это угол, вырезающий из окружности дугу, равную радиусу окружности. Величина угла в 1 радиан не зависит от радиуса окружности.
Кстати говоря, градусная мера угла тоже не зависит от радиуса окружности. Большая окружность, маленькая — углу в один градус без разницы. Но градус — это величина, искусственно придуманная людьми для их личного удобства! Древними вавилонянами, если мы помним.) 1/360 часть окружности. Так уж сложилось чисто исторически. А если бы по каким-то причинам договорились на 100 частей разбить окружность? Или на 200? Кто знает, что тогда называлось бы градусом сегодня… Вот на сколько частей разобьём окружность, такой «градус» и получим. А вот радиан — штука универсальная!) К способу разбиения окружности никак не привязан. Строго дуга, равная радиусу! И чем больше радиус, тем больше (по длине) будет и соответствующая вырезаемая дуга. И наоборот. Но сама величина угла в один радиан не меняется. И разбиение окружности (любой!) радианами — всегда одинаковое. И сейчас мы в этом лично убедимся.)
Как переводить радианы в градусы и обратно?
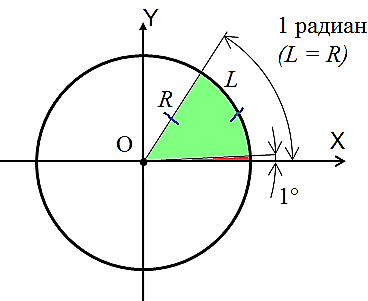
К этому моменту вам уже должно быть интуитивно понятно, что один радиан существенно больше одного градуса. Всё-таки непонятно? Тогда смотрим снова на картинку:
Будем считать, что малюсенький красный угол имеет величину примерно один градус. Совсем крохотный уголок, почти и нет его… А большой зелёный угол — примерно один радиан! Чувствуете разницу?) Конечно же, один радиан сильно больше одного градуса…
А вот теперь начинается самое интересное! Вопрос: а во сколько раз один радиан больше одного градуса? Или сколько градусов в одном радиане? Сейчас выясним!)
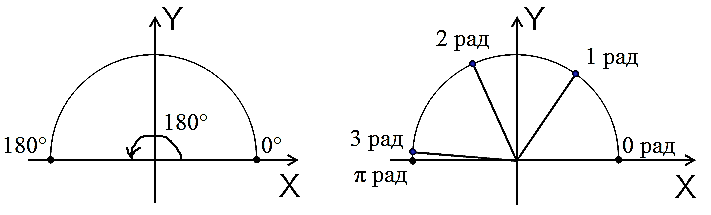
Смотрим на очередные картинки:
На картинке слева изображён полукруг. Обычный развёрнутый угол величиной 180°. А вот на картинке справа — тот же самый полукруг, но нарезанный радианами! Видно, что в 180° помещается примерно три с хвостиком радиана.
Вопрос на засыпку: как вы думаете, чему равен этот хвостик?)
Да! Он равен 0,141592653… Привет, число «пи», вот мы про тебя и вспомнили!)
Стало быть, в 180° укладывается 3,141592653… радиан. Понятное дело, что каждый раз писать такое длинное число неудобно, поэтому пишут приближённо:
Вот и всё. Вот и весь секрет тотального присутствия числа «пи» в тригонометрии. Эту простую формулку надо знать железно. Уловили?)
Так сколько же градусов в одном радиане? Не вопрос! Если в «пи» радианах содержится 180 градусов, то сколько же тогда градусов сидит в одном радиане? Правильно, в «пи» раз меньше! То есть меньше примерно в 3,14 раза.
Вот и делим обе части нашего соотношения на «пи» и получаем один радиан в градусах:
Это приближённое равенство также очень полезно запомнить. В одном радиане примерно 60 градусов. Такой грубой оценки бывает вполне достаточно для ответа на очень многие каверзные вопросы, связанные с углами. Бывает и недостаточно, конечно. В своё время мы такие хитрые задачки рассмотрим.)
Но это не самое главное применение этой формулы!) А самое главное — перевод радианов в градусы и обратно.
Переводим радианы в градусы!
Чаще всего углы в тригонометрии заданы в радианах с числом «пи». Это — самая стандартная ситуация. Если угол задан в радианах с числом «пи», то всё очень просто. Мы знаем, что «пи» радиан — это 180 градусов. Вот и подставляем вместо «пи» радиан — число 180. Сокращаем всё что сокращается и получаем угол в градусах.
Или более мудрёный угол:
Переводим градусы в радианы!
Обратный перевод градусов в радианы чуть сложнее, но ненамного. Если угол задан в градусах, то сначала нам надо узнать, сколько составляет один градус в радианах. И умножить это значение на количество градусов.) И чему же равен 1° в радианах?
Вот и все дела. Умножаем дробь π /180 на количество градусов, сокращаем что сокращается и получаем угол в радианах. Например:
Вот и всё. Заменять «пи» на примерно 3,14 никакой необходимости нет: его всегда буквой пишут. Что правда, то правда: нас же в заданиях обычно точный ответ интересует! А не приближённый.) Кстати, кому интересен приближённый ответ, посчитайте на калькуляторе. Получите примерно 0,628 и 2,356 радиана соответственно.
Итак, в непринуждённой беседе с лирическими отступлениями мы узнали, что радианы — это очень даже просто, не больно и не страшно.) Да и перевод туда-обратно несложен. И «пи» — не кусается… Так откуда же проблемы?
Это и приводит к казусам. Человек смотрит на пример, видит «пи» и автоматически считает, что это 180°. Везде и всюду. Кстати, это срабатывает. До поры до времени, пока примеры — типовые. Но любое отклонение примера от шаблона — тут же валит наповал! Почему?
Потому, что само по себе «пи» — это число! А никакие не градусы! Это «пи» радиан = 180°!
Ещё раз запоминаем:
Это заклинание надо понимать железно. Причём не просто механически зазубрить, а именно понимать каждое слово и каждый значок! И особенно — слово «радиан». Я не шучу. Ибо, если на вопрос, «Что такое «пи» в тригонометрии?», вы, блистая знаниями, радостно заявляете:
то это говорит о том, что вы не понимаете до конца смысла этой зелёной фразы. И все дальнейшие беседы уже бессмысленны, да…
Ещё раз: «пи» — это число! Примерно равное 3,14. Точного значения этого числа не знает никто: оно бесконечно длинное, корявое, иррациональное. Но — число! Такое же, как 2 или 7. Можно пройти примерно «пи» километров. Три километра и ещё около 140 метров. Можно купить «пи» килограммов картошки. Если продавец образованный встретится.) Можно выпить «пи» литров кока-колы. Если здоровье не жалко… И так далее…
Всё равно непонятна зелёная запись? Хорошо, вот вам простые житейские фразы:
1 километр — это 1000 метров;
3 часа — это 180 минут;
2 года — это 730 дней;
И тому подобное. Точно так же и с градусами/радианами:
«Пи» радиан — это 180 градусов!
Уяснили, что «пи» — это просто число? Или я уже достал вас этой заезженной фразой? Ну ладно, убедили. Тогда вот вам парочка нестандартных вопросов:
А теперь сравниваем эти два синуса. Как? По кругу, разумеется! Рисовать углы мы с вами уже умеем, что такое синус угла на круге — тоже знаем. Вперёд! Рисуем круг, углы примерно 0,79 ° и 45° и смотрим какие синусы у этих углов. Даже на самом корявом круге будет видно, что sin45° гораздо больше, чем sin0,79°.
С косинусами — всё то же самое. Рисуем на круге в правильных четвертях углы примерно 5 градусов и 5 радианов (помним, чему примерно равен один радиан в градусах?). Круг нам всё и подскажет. А именно, что cos5 меньше, чем cos5°.
Вообще, задачки с углами в радианах без «пи» (типа определить знак выражения sin10∙cos20) относятся к разряду нестандартных. В следующем уроке разберём парочку таких.)
Ну что, потренируемся с переводом углов?) Решаем несложные задания.
1. Переведите следующие углы из градусной меры в радианную:
Ответы (по возрастанию):
Как вы думаете, что это были за углы? Да! Это углы, которые попадают на координатные оси! Эти опорные значения надо держать в голове надёжно. До автоматизма! Как в градусах, так и в радианах. Зачем? Да всё за тем же! Для правильного распределения любых углов по четвертям.) Это полезное умение — залог успеха в любом задании по тригонометрии. Любом! От примитивных примеров до вполне себе солидных ЕГЭшных задачек части 2 (уравнения с отбором корней, тригонометрические неравенства и прочие хитрые штучки).
2. Переведите углы в радианную меру:
Ответы (в беспорядке):
Переведите следующие углы из радианной меры в градусную:
Ответы (в беспорядке):
300°; 225°; 120°; 330°; 240°; 135°; 210°; 315°; 150°.
А это что за углы? Правильно! Это углы, в пределах одного оборота, кратные предыдущим трём! Но не попадающие на оси координат. Такие углы вы также обязаны уметь просчитывать! И более того, все углы, кратные 30, 45 или 60 градусам, вы обязаны уметь просчитывать! Как в пределах одного оборота, так и за его пределами. Как положительные, так и отрицательные… В соответствующем уроке мы научимся с вами проделывать такие полезные вещи.
Если и это получилось, то тогда можно считать, что перевод радианов в градусы и обратно — уже не ваша проблема. Но перевод углов из одной размерности в другую — это лишь ещё один шаг вперёд к успешному постижению тригонометрии. Шаг мощный, но недостаточный. Ведь, чаще всего, с углами надо потом ещё и что-то делать.) Рисовать на круге, например. Или синус/косинус считать. Да и тангенс/котангенс тоже…
Второй серьёзный шаг — это умение правильно определять положение любого угла на тригонометрическом круге. Любого! Как в градусах, так и в радианах. С градусами на круге мы уже плотно поработали в предыдущем уроке. Теперь настал черёд набивать руку в работе с радианами.