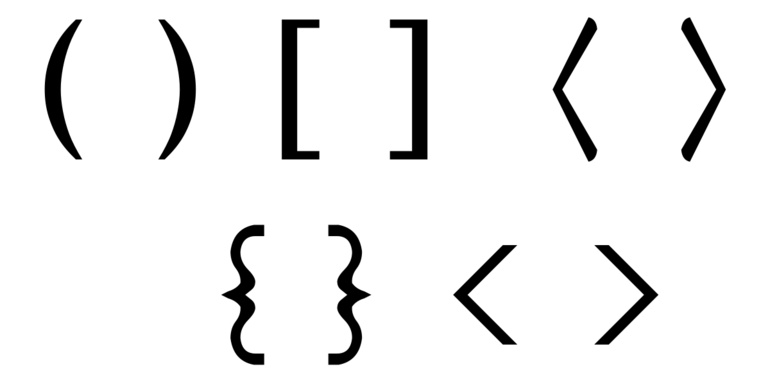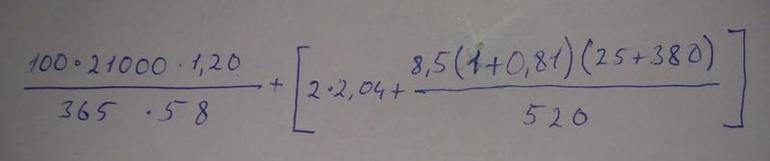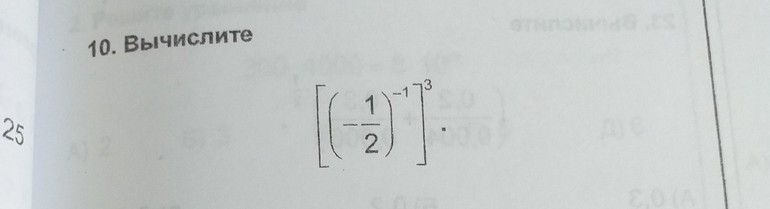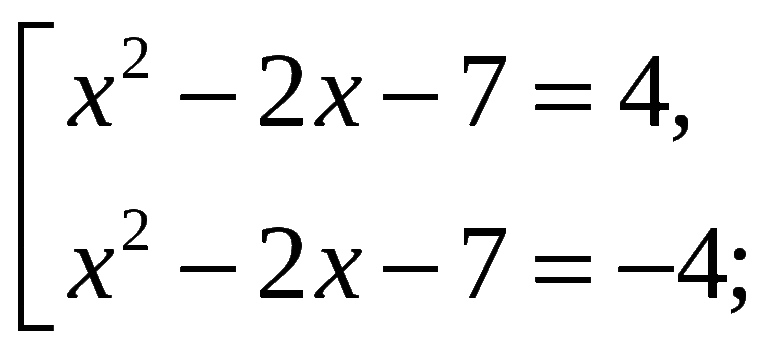Для чего нужны скобки в математике

Для чего нужны скобки в математике?

2-й класс

На уроке ознакомления с новым материалом дети должны не просто получить готовые знания, а вывести их самостоятельно, выполняя определенные действия. И чем больше таких практических действий будет совершено, тем лучше ученики усвоят новое правило.

Тема. «Выражение со скобкой».

Цели. Закреплять вычислительные навыки в пределах 20; познакомить с постановкой скобок в примерах в несколько действий, их ролью, с порядком выполнения действий в таких примерах; показать новую запись решения задачи путем составления выражения; развивать наблюдательность, логическое мышление.

Оборудование. Карточки с примерами в несколько действий.

I. Организационный момент

II. Устный счет

Учитель. Первый вариант собирает верхнюю дорожку (от 8 до до знака вопроса), а второй вариант – нижнюю. Победит тот, кто раньше других определит число, спрятавшееся под вопросом.

Дети выполняют вычисления.

– Поздравьте победителя!
А теперь откройте тетради и запишите сегодняшнее число.
Сегодня 21-е число. Охарактеризуйте его.

Дети. В числе 21 – два десятка, одна единица. Оно нечетное, двузначное. В его записи использованы две разные цифры.

У. Какие 2 двузначных числа надо сложить, чтобы получить 21?
Какие 3 однозначных числа надо сложить, чтобы получить 21?
Какие 2 однозначных числа надо умножить, чтобы получить 21?

Выслушиваются ответы детей.

III. Сообщение темы урока

У. Чтобы узнать тему нашего урока, вам надо расшифровать запись на доске.

Дети производят вычисления, пользуются шифром и читают тему урока.

– Что у вас получилось?

Д. Выражения со скобками.

У. На уроке мы постараемся ответить на вопросы: Что такое «скобка»? Какую роль играют скобки в выражениях?

IV. Чистописание

У. На минутке чистописания мы потренируемся правильно записывать разные виды математических скобок.
Скобка – знак препинания или математический знак в виде отвесной черты (закругленной, фигурной, квадратной, прямой наклонной).

Учитель показывает правильную запись скобок на доске, дети изображают их в тетрадях.

V. Знакомство с новым материалом

У. Сравните записи на доске.

– Чем похожи и чем отличаются выражения?

– Как их прочитать? Как вычислять?

Д. Если скобок нет, вычисляем, начиная слева направо.

У. Рассмотрите равенство.

– Чем похожа левая часть равенства на правую? Чем отличается?

Д. Слагаемые те же, но введены скобки.

Д. Слагаемые те же, в левой части скобки объединяют первые два слагаемых, а в правой – два последних.

У. Изменится ли порядок действий?

Д. Да, наличие скобок указывает на порядок действий.

У. В каком порядке нужно выполнять действия в левом выражении? А в правом?

– Как можно объяснить числа в сумме?

Д. Можно складывать любые два соседних слагаемых, а затем прибавлять к ним третье слагаемое.

У. Как бы вы могли найти результат в следующем выражении?

Дети выходят к доске и записывают варианты решений.

(7 + 1) + 3 + 4
7 + (1 + 3) + 4
(7 + 1 + 3) + 4
7 + (1 + 3 + 4)
7 + 1 + (3 + 4)
(7 + 1) + (3 + 4)

У. А с разностью посложнее!

(9 – 1) – (5 – 3) = 6
9 – 1 – (5 – 3) = 6
(9 – 1 – 5) – 3 = 0

– Не попадитесь в ловушку! Можно ли в выражениях, где есть разность, ставить скобки так же свободно, как с суммами?

Д. Нужно обращать внимание на то, чтобы можно было выполнить действие вычитания, то есть уменьшаемое должно быть больше вычитаемого.

У. Какое действие главнее: сложение или вычитание?

Д. Оба они равноправны.

У. Расставьте порядок действий.

У. Что нужно помнить при решении выражений со скобками?

Д. Сначала выполняют действия в скобках, а потом за скобками.

– Расставьте порядок действий.

Работа выполняется коллективно с комментированием.

– А теперь запишите выражения в тетрадь и самостоятельно укажите порядок действий.

Дети выполняют задание. Осуществляется проверка.

– Зависит ли результат выражения от порядка действий?

Д. Если не знать порядка выполнения действий в примерах со скобками, можно решить примеры неправильно.

У. А теперь выполним задание по рядам. Вы получаете карточки с математическими выражениями. В них надо указать порядок действий. Так как вычисления в данной работе производить не надо, вместо чисел в выражениях записаны нули. Каждый из вас работает с одним примером, затем передает карточку сидящему сзади.

Учитель раздает карточки. После выполнения работы дети, сидящие в разных рядах, меняются карточками и проверяют работу своих соседей. Ошибки разбираются у доски.

0 – 0 + 0
(0 + 0) – (0 – 0)
0 – 0 + 0 – 0
0 – (0 – 0 + 0)
0 + (0 – 0) – 0
(0 – 0 + 0) + 0
(0 – 0) + (0 – 0)

0 + 0 – 0
(0 – 0) + (0 – 0)
0 + (0 + 0 – 0)
(0 – 0 + 0) – 0
(0 + 0) – (0 + 0)
(0 – 0) – (0 + 0)
0 + 0 + 0 – 0

0 – (0 – 0)
0 – 0 + 0 – 0
(0 + 0) – (0 + 0)
0 – (0 + 0 – 0)
(0 – 0 + 0) – 0
0 – (0 – 0) + 0
(0 + 0 – 0) + 0

VI. Физкультминутка

VII. Закрепление нового материала

У. Предлагаю вам ответить на вопросы теста.

1. В выражении 8 – 2 + 1 действия выполняются:

а) по порядку справа налево;
б) по порядку слева направо;
в) в любом порядке.

2. Отметьте, где правильно расставлен порядок выполнения действий:

– А теперь мы будем учиться составлять и записывать математические выражения.

Один ученик работает у доски, пользуясь помощью учителя, остальные – в тетрадях.

К числу 10 прибавить разность чисел 17 и 9.

Из 12 вычесть сумму чисел 3 и 6.

Разность чисел 12 и 10 увеличить на 5.

К сумме чисел 8 и 3 прибавить разность чисел 14 и 6.

10 + (17 – 9)
(12 – 10) + 5

12 – (3 + 6)
(8 + 3) + (14 – 6)

У. А еще скобки встречаются и в таких выражениях.

х + ( – ) = 5

( + ) – а = 10

с – ( + ) = –

– Как называются такие выражения?

У. С решением уравнений со скобками вы будете знакомиться позднее.

VIII. Решение задач

У. Прочитайте задачу. Сделайте краткую запись и решите ее.

Иван Царевич и его братья выпускали стрелы. 3 стрелы упали на царский двор, 4 – на боярский, а 8 стрел улетели в неизвестном направлении. Сколько всего стрел выпустили Иван-царевич и его братья?

Два ученика работают на закрытых частях доски.

Решение задачи проверяется.

– А хотите узнать новый способ записи решения задачи? Вы умеете решать задачи по действиям. Сегодня я познакомлю вас с решением задачи путем составления выражения. Поможете мне?

Составьте условие задачи по ее краткой записи.

– Прочитайте только условие задачи! Какой вопрос можно задать?

Д. Сколько-то книг стояло на первой полке, сколько-то – на второй. Надо узнать, сколько книг на двух полках.

У. Чтобы найти, сколько всего книг на двух полках, что нужно знать?

Д. Сколько книг на первой и сколько на второй полках.

У. Какое действие для этого нужно выполнить?

У. Ставим посередине строчки знак «+». Опускаем лист вниз, открывая данные о первой полке.
– Сколько книг на первой полке, нам известно?

У. Пишем число «7» слева от знака «+».

Опускаем лист ниже, открываем данные о второй полке.
– Сколько книг на второй полке, мы знаем?

У. Справа от знака «+» ставим скобки.

– Подумаем, как же найти количество книг на второй полке, если известно, что на этой полке на 4 книги меньше?

У. Это выражение и записываем в скобках.

– Вот мы и записали решение задачи в виде одного выражения. Теперь нужно сосчитать, сколько получится книг.

IХ. Итог урока

У. Что нового вы узнали на уроке? Для чего применяются скобки в математике?

Х. Домашнее задание

1. Составить задачу и решить ее с помощью выражения.

2. Составить 5 математических выражений со скобками из 4–5 чисел для соседа, записать их на карточке.

Источник

Скобки в математике

Вы будете перенаправлены на Автор24

Скобки в математике играют очень важную роль: с помощью них задаётся порядок действий с выражением, обозначаются границы промежутков и необходимость выполнения какого-либо действия над выражением. Также с помощью скобок обозначаются вектора и матрицы и действия с множествами.

Использование круглых скобок в математике

Круглые скобки в математике встречаются наиболее часто, и они используются для множества целей.

Первое применение.

С помощью круглых скобок устанавливается порядок действий для вычисления алгебраического выражения. Выражение, которое стоит в скобках, вычисляется первым, за ним следует вычисление всех остальных.

В случае же если в выражении скобок много и одна находится внутри другой — первыми вычисляются скобки с максимальной глубиной вложенности.

Второе применение.

Третье применение.

Круглые скобки также используются для обозначения действий, которые необходимо совершить над всем выражением, стоящим в скобках. Под действием здесь имеются в виду возведение в степень, взятие производной или вычисление подинтегрального выражения.

$(x+2)^2; \int_1^5 (x^2+5x)dx; f’(x)= (5x^2 + 1)’$

Четвёртое применение.

Пятое применение.

Готовые работы на аналогичную тему

Пятое применение.

Квадратные скобки в математике

Что же означают квадратные скобки в математике и для чего они используются?

Квадратные скобки в математике встречаются реже чем круглые, но всё же их можно встретить довольно часто.

Первое применение.

Квадратные скобки иногда используются при записи выражений наряду с круглыми для того, чтобы было проще различить скобки и, соответственно, задаваемый ими порядок действий. Часто с такой целью квадратные скобки используются для записи формул физики и других технических наук.

Второе применение.

Третье применение.

С помощью квадратной скобки записывают совокупности. Совокупности — это системы уравнений, для которых справедливы все множества решений для каждого уравнения, входящего в совокупность.

$\left [ \begin x +32=2y \\ y^2-12=0 \\ \end\right.$

Фигурная скобка в математике

Первое применение.

С помощью символа фигурной скобки обозначают систему уравнений, решением которой являются корни, подходящие для всех уравнений, включённых в систему.

Второе применение.

Третье применение.

Треугольные скобки

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 06 03 2021

Источник

Общая характеристика

Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.

Значение и разновидности

Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.

В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.

Разновидности:

Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.

В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.

Основные цели квадратной скобки в математике:

Другие варианты расчета:

Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.

Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.

Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.

На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.