Для чего нужны вейвлеты

Основы теории вейвлет-преобразования

Введение

Некоторые идеи теории вейвлетов появились очень давно. Например, уже в 1910 году А.Хаар опубликовал полную ортонормальную систему базисных функций с локальной областью определения (теперь они называются вейвлетами Хаара). Первое упоминание о вейвлетах появилось в литературе по цифровой обработке и анализу сейсмических сигналов (работы А.Гроссмана и Ж.Морле).

В последнее время возникло и оформилось целое научное направление, связанное с вейвлет-анализом и теорией вейвлет-преобразования. Вейвлеты широко применяются для фильтрации и предварительной обработки данных, анализа состояния и прогнозирования ситуации на фондовых рынках, распознавания образов, при обработке и синтезе различных сигналов, например речевых, медицинских, для решения задач сжатия и обработки изображений, при обучении нейросетей и во многих других случаях.

Несмотря на то, что теория вейвлет-преобразования уже в основном разработана, точного определения, что же такое «вейвлет», какие функции можно назвать вейвлетами, насколько мне известно, не существует. Вейвлеты могут быть ортогональными, полуортогональными, биортогональными. Эти функции могут быть симметричными, асимметричными и несимметричными.

Различают вейвлеты с компактной областью определения и не имеющие таковой. Некоторые функции имеют аналитическое выражение, другие – быстрый алгоритм вычисления связанного с ними вейвлет-преобразования. Попробуем дать вначале неформальное определение вейвлет-преобразования, а затем – его точное математическое обоснование.

Вейвлеты и многомасштабный анализ

Рассмотрим задачу, которая очень часто встречается на практике: у нас есть сигнал (а сигналом может быть все, что угодно, начиная от записи показаний датчика и кончая оцифрованной речью или изображением). Идея многомасштабного анализа (multiscale analysis, multiresolutional analysis) заключается в том, чтобы взглянуть на сигнал сначала вплотную – под микроскопом, затем через лупу, потом отойти на пару шагов, потом посмотреть издалека (рис.1).

Что это нам дает? Во-первых, мы можем, путем последовательного огрубления (или уточнения) сигнала выявлять его локальные особенности (ударение в речи или характерные детали изображения) и подразделять их по интенсивности. Во-вторых, таким образом обнаруживается динамика изменения сигнала в зависимости от масштаба.

Если резкие скачки (например, аварийное отклонение показаний датчика) во многих случаях видны «невооруженным глазом», то взаимодействия событий на мелких масштабах, перерастающие в крупномасштабные явления (так, мощный транспортный поток состоит из движения многих отдельных автомобилей), увидеть очень сложно. И наоборот, сосредоточившись только на мелких деталях, можно не заметить явлений, происходящих на глобальном уровне.

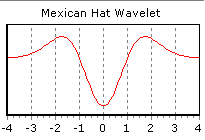
Идея применения вейвлетов для многомасштабного анализа заключается в том, что разложение сигнала производится по базису, образованному сдвигами и разномасштабными копиями функции-прототипа (то есть вейвлет-преобразование по своей сути является фрактальным). Такие базисные функции называются вейвлетами (wavelet), если они определены на пространстве L 2 (R) (пространство комплекснозначных функций f(t) на прямой с ограниченной энергией), колеблются вокруг оси абсцисс и быстро сходятся к нулю по мере увеличения абсолютного значения аргумента (рис.2).

Оговоримся сразу, что это определение не претендует на полноту и точность, а дает лишь некий «словесный портрет» вейвлета. Таким образом, свертка сигнала с одним из вейвлетов позволяет выделить характерные особенности сигнала в области локализации этого вейвлета, причем чем больший масштаб имеет вейвлет, тем более широкая область сигнала будет оказывать влияние на результат свертки.

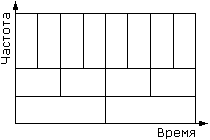
Согласно принципу неопределенности, чем лучше функция сконцентрирована во времени, тем больше она размазана в частотной области. При перемасштабировании функции произведение временного и частотного диапазонов остается постоянным и представляет собой площадь ячейки в частотно-временной (фазовой) плоскости.

Преимущество вейвлет-преобразования перед, например, преобразованием Габора заключается в том, что оно покрывает фазовую плоскость ячейками одинаковой площади, но разной формы (рис.3). Это позволяет хорошо локализовать низкочастотные детали сигнала в частотной области (преобладающие гармоники), а высокочастотные – во временной (резкие скачки, пики и т.п.).

Более того, вейвлет-анализ позволяет исследовать поведение фрактальных функций – то есть не имеющих производных ни в одной своей точке!

Ортогональное вейвлет-преобразование

Вейвлет-преобразование несет огромное количество информации о сигнале, но, с другой стороны, обладает сильной избыточностью, так как каждая точка фазовой плоскости оказывает влияние на его результат.

Вообще говоря, для точного восстановления сигнала достаточно знать его вейвлет-преобразование на некоторой довольно редкой решетке в фазовой плоскости (например, только в центре каждой ячейки на рис.3). Следовательно, и вся информация о сигнале содержится в этом довольно небольшом наборе значений.

Идея здесь заключается в том, чтобы масштабировать вейвлет в некоторое постоянное (например, 2) число раз, и смещать его во времени на фиксированное расстояние, зависящее от масштаба. При этом все сдвиги одного масштаба должны быть попарно ортогональны – такие вейвлеты называются ортогональными.

При таком преобразовании выполняется свертка сигнала с некоторой функцией (так называемой скейлинг-функцией, о ее свойствах мы расскажем позже) и с вейвлетом, связанным с этой скейлинг-функцией. В результате мы получаем «сглаженную» версию исходного сигнала и набор «деталей», отличающих сглаженный сигнал от исходного.

Последовательно применяя такое преобразование, мы можем получить результат нужной нам степени детальности (гладкости) и набор деталей на разных масштабах – то, о чем говорили в начале статьи. Более того, применив вейвлет-преобразование к заинтересовавшей нас детали сигнала, мы можем получить ее «увеличенное изображение». И наоборот, отбросив несущественные детали и выполнив обратное преобразование, мы получим сигнал, очищенный от шумов и случайных выбросов (например, «убрать» случайно попавшую в кадр птицу на фотографии здания).

Дискретное вейвлет-преобразование и другие направления вейвлет-анализа

Очевидно, идея использовать вейвлет-преобразование для обработки дискретных данных является весьма привлекательной (дискретизация данных необходима, например, при их обработке на ЭВМ). Основная трудность заключается в том, что формулы для дискретного вейвлет-преобразования нельзя получить просто дискретизацией соответствующих формул непрерывного преобразования.

К счастью, И.Добеши удалось найти метод, позволяющий построить (бесконечную) серию ортогональных вейвлетов, каждый из которых определяется конечным числом коэффициентов. Стало возможным построить алгоритм, реализующий быстрое вейвлет-преобразование на дискретных данных (алгоритм Малла). Достоинство этого алгоритма, помимо всего вышесказанного, заключается в его простоте и высокой скорости: и на разложение, и на восстановление требуется порядка cN операций, где с – число коэффициентов, а N – длина выборки.

В последнее время теория вейвлет-преобразования переживает просто революционный рост. Появились и развиваются такие направления, как биортогональные вейвлеты, мультивейвлеты, вейвлет-пакеты, лифтинг и т.д.

Применение вейвлет-преобразования

В заключение нашей статьи перечислим некоторые области, где использование вейвлетов может оказаться (или уже является) весьма перспективным.

И это еще далеко не все!

Заключение

Несмотря на то, что математический аппарат вейвлет-анализа хорошо разработан и теория, в общем, оформилась, вейвлеты оставляют обширное поле для исследований. Достаточно сказать, что выбор вейвлета, наиболее подходящего для анализа конкретных данных, представляет собой скорее искусство, чем рутинную процедуру. Кроме того, огромное значение имеет задача разработки приложений, использующих вейвлет-анализ – как в перечисленных областях, так и во многих других, перечислить которые просто не представляется возможным.

Источник

Вейвлет — анализ.Часть 1

Введение

Рассмотрим дискретное вейвлет – преобразования (DWT), реализованное в библиотеке PyWavelets PyWavelets 1.0.3. PyWavelets — это бесплатное программное обеспечение с открытым исходным кодом, выпущенное по лицензии MIT.

При обработке данных на компьютере может выполняться дискретизированная версия непрерывного вейвлет-преобразования, основы которого описаны в моей предыдущей статье. Однако, задание дискретных значений параметров (a,b) вейвлетов с произвольным шагом Δa и Δb требует большого числа вычислений.

Кроме того, в результате получается избыточное количество коэффициентов, намного превосходящее число отсчетов исходного сигнала, которое не требуется для его реконструкции.

Дискретное вейвлет – преобразование (DWT), реализованное в библиотеке PyWavelets, обеспечивает достаточно информации как для анализа сигнала, так и для его синтеза, являясь вместе с тем экономным по числу операций и по требуемой памяти.

Когда нужно использовать вейвлет-преобразование вместо преобразования Фурье

Преобразования Фурье будет работать очень хорошо, когда частотный спектр стационарный. При этом частоты, присутствующие в сигнале, не зависят от времени, и сигнал содержит частоты xHz, которые присутствует в любом месте сигнала. Чем нестационарнее сигнал, тем хуже будут результаты. Это проблема, так как большинство сигналов, которые мы видим в реальной жизни, нестационарны по своей природе.

Преобразование Фурье имеет высокое разрешение в частотной области, но нулевое разрешение во временной области. Покажем это на следующих двух примерах.

На этом графике все четыре частоты присутствуют в сигнале в течении всего времени его действия.

На этом графике сигналы не перекрываются во времени, боковые лепестки обусловлены разрывом между четырьмя различными частотами.

Для двух частотных спектров, содержащих точно такие же четыре пика, преобразование Фурье не может определить, где в сигнале эти частоты присутствуют. Лучшим подходом для анализа сигналов с динамическим частотным спектром является вейвлет-преобразования.

Основные свойства вейвлетов

Выбор типа, а следовательно свойств вейвлета, зависит от поставленной задачи анализа, например, для определения действующих значений токов в электроэнергетике большую точность обеспечивают вейвлеты Ингрид Добеши больших порядков. Свойства вейвлетов можно получить используя функцию pywt.DiscreteContinuousWavelet() в следующем листинге:

discrete_wavelets-[‘db5’, ‘sym5’, ‘coif5’, ‘haar’]

В ряде практических случаев возникает необходимость получить информацию о центральной частоте psi вейвлет – функции, которая используется, например, при вейвлет-анализе сигналов для выявления дефектов в зубчатых передачах:

Пользуясь центральной частотой материнского вейвлета и масштабным коэффициентом «a» можно преобразовывать шкалы в псевдо частоты используя уравнение:

Режимы расширения сигнала

Перед вычислением дискретного вейвлет-преобразования с использованием банков фильтров возникает необходимость удлинить сигнал. В зависимости от метода экстраполяции, на границах сигнала могут возникнуть существенные артефакты, приводящие к неточностям DWT преобразования.

PyWavelets предоставляет несколько методов экстраполяции сигнала, которые могут быть использованы для минимизации указанного негативного эффекта. Для демонстрации таких методов используем следующий листинг:

На графиках показано, как короткий сигнал (красный) расширяется (черный) за пределами своей первоначальной протяженности.

Дискретное вейвлет – преобразование

Для демонстрации DWT будем использовать сигнал с динамическим частотным спектром, который со временем увеличивается. Начало сигнала содержит низкочастотные значения, а конец сигнала содержит частоты коротковолнового диапазона. Это позволяет нам легко определить, какая часть частотного спектра отфильтрована, просто взглянув на временную ось:

Дискретное вейвлет-преобразование в PyWavelets 1.0.3 это функция pywt.dwt(), которая вычисляет аппроксимирующие коэффициенты cA и детализирующие коэффициенты cD первого уровня вейвлет-преобразования сигнала, заданного вектором:

Коэффициенты аппроксимации (cA) представляют выход фильтра нижних частот (фильтра усреднения) DWT. Коэффициенты детализации (cD) представляют выход фильтра высоких частот (разностного фильтра) DWT.

Можно использовать функцию pywt.wavedec()для немедленного расчета коэффициентов более высокого уровня. Эта функция принимает за вход исходный сигнал и уровень и возвращает один набор коэффициентов аппроксимации (n-го уровня) и n наборов коэффициентов детализации (от 1 до n-го уровня). Вот пример для пятого уровня:

В результате получаем те же графики, что и в предыдущем примере. Можно получить отдельно коэффициенты cA и cD:

Банк фильтров

Часть вопросов, касающихся уровней преобразования, мы рассмотрели в предыдущем разделе. Однако, DWT всегда реализуется как банк фильтров в виде каскада высокочастотных и низкочастотных фильтров. Банки фильтров являются очень эффективным способом разделения сигнала на несколько частотных поддиапазонов.

На первом этапе с малым масштабом анализируя высокочастотное поведение сигнала. На втором этапе шкала увеличивается с коэффициентом два (частота уменьшается с коэффициентом два), и мы анализируем поведение около половины максимальной частоты. На третьем этапе масштабный фактор равен четырем, и мы анализируем частотное поведение около четверти максимальной частоты. И это продолжается до тех пор, пока мы не достигнем максимального уровня разложения.

Максимальный уровень декомпозиции можно вычислить при помощи функции pywt.wavedec(), при этом декомпозиция и детализация будет иметь вид:

Максимальный уровень декомпозиции: 7

Декомпозиция останавливается, когда сигнал становится короче, чем длина фильтра для данного вейвлета sym5. Для примера предположим, что у нас есть сигнал с частотами до 1000 Гц. На первом этапе мы разделяем наш сигнал на низкочастотную и высокочастотную части, т. е. 0-500 Гц и 500-1000 Гц. На втором этапе мы берем низкочастотную часть и снова разделяем ее на две части: 0-250 Гц и 250-500 Гц. На третьем этапе мы разделили часть 0-250 Гц на часть 0-125 Гц и часть 125-250 Гц. Это продолжается до тех пор, пока мы не достигнем максимального уровня декомпозиции.

Анализ wav файлов с использованием fft Фурье и вейвлет скалограммы

Для анализа воспользуемся файлом WebSDR. Рассмотрим анализ приведенного сигнала средствами triang из scipy.signal и реализацию дискретного преобразования Фурье в python (fft из scipy.fftpack). Если длина последовательности fft не будет равна 2n, то вместо быстрого преобразования Фурье (fft) будет выполняться дискретное преобразование Фурье (dft). Именно таким образом работает эта команда.

Используем буфер быстрого преобразования Фурье по следующей схеме (численные данные для примера):

fftbuffer=np.zeros(15); создаем буфер, заполненный нулям;
fftbuffer [:8]=x [7:]; перемещаем конец сигнала в первую часть буфера; fftbuffer [8:]=x [:7]—перемещаем начало сигнала в последнюю часть буфера; X=fft(fftbuffer) — считаем преобразование Фурье буфера, заполненного значениями сигнала.

Чтобы фазовый спектр был более читаем, применим развертывание фазы. Для этого изменим строку с расчетом фазовой характеристики: pX=np.unwrap(np.angle(X)).

Для сравнительного анализа воспользуемся вейвлет скалограммой, которую можно построить с использованием функции tree = pywt.wavedec(signal, ‘coif5’) в matplotlib.

Таким образом, скалограмма дает более детальный ответ на вопрос о распределении частот во времени, а быстрое преобразование Фурье отвечает за сами значения частот. Всё зависит от поставленной задачи даже для такого простого примера.

Источник

Вейвлет – анализ. Часть 2

Введение

В данной публикации рассматривается вейвлет – анализ временных рядов. Основная идея вейвлет-преобразования отвечает специфике многих временных рядов, демонстрирующих эволюцию во времени своих основных характеристик – среднего значения, дисперсии, периодов, амплитуд и фаз гармонических компонент. Подавляющее большинство процессов, изучаемых в различных областях знаний, имеют вышеперечисленные особенности.

Целью настоящей публикации является описание методики непрерывного вейвлет- преобразования временных рядов средствами библиотеки PyWavelets..

Инженер-геофизик Д. Морле в конце 70-х годов XX в. столкнулся с проблемой анализа сигналов от сейсмодатчиков, которые содержали высокочастотную компоненту (сейсмическая активность) в течение короткого промежутка времени и низкочастотные составляющие (спокойное состояние земной коры) – в течение длительного периода. Оконное преобразование Фурье позволяет анализировать либо высокочастотную составляющую, либо низкочастотную составляющую, но не обе составляющие сразу.

Поэтому, был предложен метод анализа, в котором ширина оконной функции для низких частот увеличивалась, а для высоких частот – уменьшалась. Новое оконное преобразование получалось в результате растяжения (сжатия) и смещения по времени одной порождающей (так называемой скейлинг-функции – scaling function, scalet) функции. Эта порождающая функция была названа вейвлетом Д. Морле.

Непрерывное вейвлет-преобразование (CWT)

Одноуровневое вейвлет – преобразование:

coefs, frequencies =pywt.cwt(data, scales, wavelet)

scales (array_like):- Масштаб вейвлета для использования. Можно использовать соотношение f =scale2frequency(scale, wavelet)/sampling_period и определить какая физическая частота f. Здесь, f в hertz когда sampling_period в секундах;

wavelet (Wavelet object or name): — Вейвлет для использования;

sampling_period (float):- Период дискретизации для выходных частот (необязательный параметр). Значения, вычисленные для coefs, не зависят от выбора sampling_period (т. е. scales не масштабируется выборкой периода.);

coefs (array_like):- Непрерывное вейвлет — преобразование входного сигнала для заданных масштабов и вейвлет;

frequencies (array_like ):- Если единица периода выборки секунды и задана, то частоты выводятся в hertz. В противном случае предполагается период выборки, равный 1.

Примечание: Размер массивов коэффициентов зависит от длины входного массива и длин заданных масштабов.

Получим список доступных имен вейвлетов, совместимых с cwt:

[‘cgau1’, ‘cgau2’, ‘cgau3’, ‘cgau4’, ‘cgau5’, ‘cgau6’, ‘cgau7’, ‘cgau8’, ‘cmor’, ‘fbsp’, ‘gaus1’, ‘gaus2’, ‘gaus3’, ‘gaus4’, ‘gaus5’, ‘gaus6’, ‘gaus7’, ‘gaus8’, ‘mexh’, ‘morl’, ‘shan’]

Для вейвлет — анализа выбор материнского вейвлета является одной из ключевых задач. Поэтому, перед каждым выбором вейвлета просто необходимо пользоваться следующей программой, позволяющей определить динамические свойства вейвлета:

Далее будем рассматривать вейвлет-функции и их свойства с использованием приведенной программы:

Мексиканская шляпа вейвлет «mexh»:

Комплексный вейвлет Морле «cmorB-C»

где B — пропускная способность; C — центральная частота.

Здесь и далее (без специального указания) величины B,C задаются с плавающей точкой.

Гауссовы вейвлеты «gausP»

где: P — целое число от 1 до 8 вставляется в имя вейвлета, например «gaus8»; C- встроенная константа нормализации.

Комплексные гауссовы вейвлеты «cgauP»

где: P — целое число от 1 до 8 вставляется в имя вейвлета, например «сgaus8» и соответствуют порядку производной от вейвлет функции; C- встроенная константа нормализации.

Вейвлеты Шеннона «shanB-C»

где: B — ширина полосы; C — центральная частота.

CWT в PyWavelets применяется к дискретным данным — свертки с образцами интеграла вейвлета. Если scale слишком мало, то мы получаем дискретный фильтр с неадекватной выборкой, приводящий к сглаживанию, как показано на графике для вейвлета ‘cmor1.5-1.0’.

В левой колонке на графиках показаны дискретные фильтры, используемые в свертке при различных шкалах. Правый столбец — соответствующие спектры мощности Фурье каждого фильтра. При шкалах 1 и 2 для графика ‘cmor1.5-1.0’ видно, что сглаживание происходит из-за нарушения ограничение Найквиста. Указанное явление может возникнуть и у других вейвлетов при выборе С и B, поэтому при работе с вейвлетами необходимо пользоваться программой – листинг 1.

Чтобы связать заданный масштаб с определенной частотой сигнала, период дискретизации сигнала должен быть известен. При помощи функции pywt.scale2frequency() можно преобразовать список масштабов в соответствующие частоты. Правильный выбор масштабов зависит от выбранного вейвлета, поэтому pywt.scale2frequency() следует использовать для получения представления о соответствующем частотном диапазоне сигнала.

array([100., 50., 33.33333333, 25. ])

Вейвлет — анализ временных рядов средствами CWT PyWavelets

Набор данных el-Nino представляет собой набор данных временных рядов, используемый для отслеживания El Nino и содержит ежеквартальные измерения температуры морской поверхности с 1871 по 1997 год. Чтобы понять силу масштабограммы, давайте визуализируем ее для набора данных el-Nino вместе с исходными данными временных рядов и его преобразованием Фурье.

Для вейвлет-анализа временных рядов необходимо выполнить следующие действия по пунктам:

1. Выбрать материнский вейвлет: Выбираем комплексный вейвлет Морле «cmorB-C»:

Пропускную способность – B и центральную частоту – С которого будем определять на следующем этапе.

2. Определить центральную частоту, приняв dt=0.25 для нашего временного ряда:

3. Находим преобразование Фурье материнского вейвлета cmor1.0-0.5 (используем листинг 1):
Непрерывный вейвлет будет оцениваться во всем диапазоне [-8.0, 8.0]

4. Выбираем данные для временного ряда:

Данные — это ежеквартальные измерения температуры морской поверхности с 1871 по 1997 год. Для этих данных: t0=1871 dt=0.25

5. Строим временной ряд с сигналом и его скользящее среднее на одном графике:

6. Проводим преобразование Фурье и модности спектра от временного ряда:

7. Определяем масштабы: scales = arange(1, 128); levels = [2**-4, 2**-3, 2**-2, 2**-1, 2**0, 2**1, 2**2, 2**3].

8. Строим масштабограмму:

На масштабограмме видно, что большая часть мощности спектра сконцентрирована за период 2-8 лет, это соответствует частоте 0,125 – 0,5 Гц. В спектре Фурье модность так же концентрируется вокруг этих значений частоты. Однако вейвлет — преобразование также дает нам временную информацию, а преобразование Фурье — нет.

Например, на масштабной диаграмме мы видим, что до 1920 года было много колебаний, в то время как между 1960 и 1990 годами их было не так много. Мы также можем видеть, что с течением времени происходит сдвиг от более коротких периодов к более длинным.

Использование модуля scaleogram

Scaleogram-удобный инструмент для анализа 1D данных с непрерывным вейвлет — преобразованием построен на базе библиотеки PyWavelets. Модуль призван обеспечить надежный инструмент для быстрого анализа данных.

Scaleogram имеет следующие особенности:

При этом появляется следующее предупреждение:

nino3 = pd.read_table(nino3)
что приводит к предупреждению:
Warning (from warnings module):
File «C:/Users/User/Desktop/wavelet/pr.py», line 7
nino3 = pd.read_table(nino3)
FutureWarning: read_table is deprecated, use read_csv instead, passing sep=’\t’

Обращение к данным должно быть записано вот так:

Чтобы показать использование скалограммы и сравнить результаты с результатами предыдущего примера, воспользуемся теми же данными — по ежеквартальным измерениям температуры морской поверхности с 1871 по 1997 год. Для этих данных: t0=1871 dt=0.25

Если сравнивать масштабограмму с полученной сканограммой, то, за исключением цветовой палитры, они идентичны, а следовательно показывают одинаковую динамику временного ряда.
Листинг 5 проще листинга 3 и имеет большее быстродействие.

Когда частотный спектр и спектр мощности по Фурье не позволяют получить дополнительную информацию о динамике временного ряда, тогда использование скалограммы является предпочтительным.

Источник