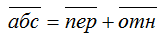Для чего применяется формула чебышева

4. 1. 003 Теория механизмов Чебышёва

4.1 Математика, механика

4.1.003 Теория механизмов Чебышёва

Математик, механик, педагог; доктор математики и астрономии; основатель и глава Петербургской математической школы, породившей, в свою очередь, русские математические школы — в теории вероятностей, теории чисел, теории приближения функций, теории механизмов; профессор Петербургского университета, академик Петербургской АН, почетный член всех российских университетов, член 25 академий и научных обществ мира; член Ученого комитета Министерства просвещения, рецензент учебников, составитель программы и инструкций для начальных и средних школ; кавалер Командорского креста Почетного легиона, лауреат Демидовской премии Петербургской АН; действительный тайный советник — Пафнутий Львович Чебышёв (1821—1894) является автором классических работ в механике, геометрии, баллистике, теории механизмов. Бесценен вклад ученого в интегральное исчисление, теорию вероятностей, теорию чисел. Чебышёв — основоположник теории приближения функций.

Пафнутия Львовича Чебышёва виднейшие ученые мира называли «гордостью науки в России, одним из величайших геометров всех времен», «гениальным математиком и одним из величайших аналистов всех времен» (Ш. Эрмит, М.Г. Миттаг-Леффлер).

Прямо говорили, что «для получения новых результатов в вопросе распределения простых чисел требуется ум, настолько превосходящий ум Чебышёва, насколько ум Чебышёва превосходит ум обыкновенного человека» (Д.Д. Сильвестр).

Русские ученые в один голос заявляли, что Чебышёв является «украшением нашей Академии», а все его труды «носят отпечаток гениальности». (http://matem.ok.nov.ru/).

Что характерно, среди панегиристов были и чистые математики-аналисты, и математики-прикладники, и геометры и техники. Практически во всех областях механики и математики Чебышёв получил фундаментальные результаты, выдвинул столько новых идей и методов, и так далеко определил развитие этих ветвей науки, что они и по сей день сохранили свое значение.

Три главных направления научной деятельности Чебышёва: теория чисел, теория вероятностей и теория механизмов равновелики — и сами по себе и своим влиянием на развитие науки «в мировом масштабе».

В каждом из них математик «изобрел новые методы для решения трудных вопросов, которые были поставлены давно и оставались нерешенными. Вместе с тем он поставил ряд новых вопросов, над разработкой которых трудился до конца своих дней» (академики А.А. Марков, И.Я. Сонин).

Выберем посему область, что поближе к нашей повседневной практике — теорию механизмов, но не забудем указать и самые значительные труды ученого из других сфер науки. Это — докторская диссертация Пафнутия Львовича «Теория сравнений» (1849), полвека служившая учебником для высшей школы; две статьи «Об определении числа простых чисел, не превосходящих данной величины» и «О простых числах» (1850), ставшие началом его теории чисел; работа «О средних величинах» (1867), легшая в основу теории вероятностей; трактаты «О функциях, наименее уклоняющихся от нуля» (1857), «Теория наилучшего приближения функции многочленами», явившиеся основанием теории приближений.

40 лет Чебышёв сотрудничал с военным артиллерийским ведомством, для которого выполнил ряд блестящих работ по усовершенствованию дальнобойности и точности артиллерийской стрельбы.

В исследовании «О черчении географических карт» (1856) Чебышёв поставил базовую задачу картографии (и начал решать ее) — найти картографическую проекцию любой страны, сохраняющую подобие в ее отдельных частях, с минимальным искажением масштаба. (Для Европейской России погрешность задавалась менее 2 % при реально достижимой тогда более 5 %). Эта задача была решена позднее учеником Чебышёва профессором Д.А. Граве.

Всех исследований, статей и сообщений Чебышёва, в которых он самыми элементарными (с точки зрения царицы наук) средствами получил великолепные научные результаты, не перечислишь, т.к. по подсчетам библиографов этот список занимает несколько журнальных страниц.

Одних только названий классических математических соотношений, связанных с именем математика, не один десяток: многочлены Чебышёва, неравенства, множество, система функций, фильтр, механизм, функции пси и тета, сеть, формула, полиномы и т.д.

Нельзя не упомянуть и о предложении Чебышёва Петербургской АН — избрать членом-корреспондентом С.В. Ковалевскую, а также о его учениках — А.М. Ляпунове, А.А. Маркове, В.А. Стеклове, Д.А. Граве, Г.Ф. Вороном, А.Н. Коркине, Е.И. Золотареве. Будущие академики и главы других математических школ завершили проработки и идеи учителя — по теории фигур равновесия вращающейся жидкости, по теории цепей и т.д.

Пафнутий Львович любые теоретические проблемы математики старался увязать с практической деятельностью людей. Не раз подчеркивая, что в любом деле надо по возможности добиваться как можно большей выгоды, Чебышёв свои математические открытия совершил при решении прикладных задач. Более того, теории механизмов и машин ученый отдал едва ли не треть своей жизни. Глубокие теоретические изыскания в этой области математик успешно сочетал с конструированием конкретных механизмов.

Ряд теоретических работ Чебышёва: «Об одном механизме», «О зубчатых колесах», «О центробежном уравнителе», «О кройке платьев» и т.п. были воплощены в конкретные машины и устройства.

Помимо этих сугубо практических вопросов Чебышёв вывел несколько сложнейших соотношений: структурную формулу плоских механизмов — т.н. формулу Грюблера (немецкий ученый, «открывший» ее на 14 лет позднее Чебышёва), теорему о существовании трехшарнирных четырехзвенников, описывающих одну и ту же шатунную кривую, нашедшую широкое применение на практике и т.д.

Многочисленные работы Чебышёва посвятил синтезу шарнирных механизмов, в частности параллелограмму Уатта, изучение которого натолкнуло математика на постановку задачи о наилучшем приближении функций.

Решив эту задачу, Чебышёв создал механизмы, в которых криволинейное движение свел к недостижимому ранее — прямолинейному (в некотором приближении), что вывело конструирование шарниров на принципиально новый уровень, а сами шарниры сделало значительно долговечнее.

Ученый построил также немало механизмов, одним своим названием говорящих об их неординарности: парадоксальный механизм, механизмы с остановками, «выпрямители движения» и т.д.

Всего ученый создал 41 оригинальный механизм и 40 их модификаций. Многие из них применяются ныне в современном автомато- и приборостроении.

На международной промышленной выставке в Чикаго (1893) Чебышёв представил свои конструкторские разработки, произведшие на посетителей неизгладимое впечатление: «стопоходящую» машину, воспроизводящую шаги четвероногого животного, самоходное кресло, лодку с гребным механизмом, сортировку для зерна, центробежный регулятор, быструю счетную машину (арифмометр), выполнявшую четыре арифметических действия.

Поговаривали даже, что академик изобрел «перпетуум мобиле» и ходящего деревянного «человека» (прообраз Буратино?)…

Все эти «чудеса» были созданы Чебышёвым не ради эффекта, а для очень конкретных и жизненно необходимых вещей. Так, например, сортировалка была сконструирована для сортировки зерна с целью отобрать лучшие — более тяжелые зерна; стопоходящая машина стала первым в мире шагающим автоматом с шарнирным механизмом, переводящим движение по окружности в прямолинейное движение (прототип советского «лунохода»); «велосипед» продемонстрировал идею ножного привода; наконец, арифмометр явился первой вычислительной машиной непрерывного действия…

Закончить очерк хочется теми же словами, которыми и начал его — России есть кем и есть чем гордиться, пока в ней есть такие люди, как П.Л. Чебышёв и созданная им русская школа математики.

Источник

Формула П. Л. Чебышева для плоских механизмов

Структурная группа (группа Ассура)

Структурная группа (группа Ассура) – это такая кинематическая цепь, присоединение которой к любому механизму не изменяет его числа степеней свободы. При этом такая цепь не должна распадаться на более простые цепи с тем же свойством. Так как группа Ассура не изменяет числа степеней свободы механизма после присоединения к нему или отсоединения от него, то она обладает собственной нулевой степенью свободы. Таким образом:W_гр=3n_гр–2p_5гр=0, откуда p_5гр=3_nгр/2 или n_гр=2p_5гр/3,где:n_гр – число звеньев в группе Ассура, включая фиктивные звенья, полученные при замене высших пар, p_5гр – число кинематических пар пятого класса в группе Ассура, включая пары, полученные при замене высших пар. Примечание: рассматриваются структурные группы, включающие только низшие пары 5 класса, т.к. при наличии высших кинематических пар в механизме их можно заменить цепями с низшими парами. Так как количество звеньев и кинематических пар заведомо целые числа, то число звеньев в группе Ассура всегда четное, а число кинематических пар кратно трем. Таким образом группы Ассура имеют следующие сочетания чисел звеньев и кинематических пар (таблица 2.1). Класс группы Ассура определяется числом сторон замкнутого контура (многоугольника), входящего в состав этой группы. При этом все группы, имеющие два звена, относятся к группам II класса, а контур с числом сторон больше трех должен быть подвижным (т.е. иметь изменяемую форму при работе механизма).Порядок группы Ассура Порядок группы Ассура определяется числом элементов кинематических пар, которыми группа присоединяется к механизму.Группы Ассура второго класса одновременно являются группами второго порядка (иногда их называют двухповодковыми группами), но они еще подразделяются на виды.Вид группы Ассура зависит от сочетания вращательных (шарниров) и поступательных (ползунов) кинематических пар в данной группе. Всего существует пять видов групп Ассура второго класса.

8. Понятие о степени подвижности механизма
Если в пространственной к. ц., состоящей из «n» подвижных звеньев, имеются к.п. 1-ого, 2-ого,… 5-ого класса, число которых, соответственно, p₁,p₂,… p₅, то к. ц. имеет число степеней свободы, определяемое формулой А.П. Малышева.
W=6n-5p₅-4p₄-3p₃-2p₂-p₁ (3.1)
Так как любой механизм имеет одно неподвижное звено (стойку) и «n» подвижных звеньев, то формула (3.1) может использоваться для определения W пространственного механизма, где n – число подвижных звеньев, а W – степень подвижности механизма, показывающая сколько нужно иметь ведущих звеньев (двигателей) для получения определенного движения остальных его звеньев.
Для плоского механизма степень подвижности определяется по формуле Чебышева: W=3n-2p₅-p₄, (3.2)

При этом к.п. 5-ого класса существует в виде поступательных, вращательных и винтовых.

При определении W необходимо учитывать возможность наличия так называемых «пассивных» звеньев, т.е. звеньев, устраняемых без формального ущерба для кинематики анализируемого механизма (рис.8).
а) W=3·4-2·6-0=0 – с пассивным звеном,
б) W=3·3-2·4-0=1 – фактически.
Кроме того, необходимо учитывать возможность наличия избыточных связей,

Формула П. Л. Чебышева для плоских механизмов

Для плоского механизма используется формула Чебышева:

где n-число подвижных звеньев

P₄,P₅-кинематические пары с одной и с двумя наложенными связями.

По-другому эту формулу можно записать в следующем виде:

где n-общее число подвижных звеньев механизма

Рв — число высших кинематических пар

10. Кинематический анализ механизмов заключается в исследовании движения звеньев механизмов независимо от сил, вызывающих это движение. В результате этого анализа определяются положения звеньев и траектории отдельных точек звеньев; линейные скорости отдельных точек и угловые скорости звеньев; линейные ускорения отдельных точек и угловые ускорения звеньев. [1]

Кинематический анализ механизмов может выполняться аналитическими и графическими методами. [2]

Кинематический анализ механизма ведется в следующем порядке: сначала исследуется движение начальных звеньев, а затем выполняется кинематический анализ отдельных структурных групп в порядке их присоединения при образовании механизма. В этом случае в каждой структурной группе будут известны положения, скорости и ускорения тех элементов кинематических пар, к которым присоединяется данная группа. Кинематический анализ каждой группы Ассура должен начинаться с определения кинематических параметров внутренних пар группы. [3]

Кинематический анализ механизмов в общем случае предусматривает решение трех основных задач, а именно: 1) определение положений звеньев и построение траекторий отдельных точек; 2) определение скоростей точек и угловых скоростей звеньев; 3) определение ускорений точек и угловых ускорений звеньев. [4]

11. Метод планов скоростей и ускорений

Метод планов скоростей и ускорений относится к графо-аналитическим методам исследования кинематики механизмов.

Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.

Этот принцип в равной степени относится к перемещениям, скоростям и ускорениям:

Планы скоростей и ускорений обладают следующими свойствами:

— на плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана. На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает;

— отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек. Вектор относительной скорости направлен на плане к той точке, которая в индексе скорости стоит на первом месте;

— фигуры, образованные точками одного и того же жесткого звена на плане и на механизме, подобны. Поэтому, если на звене известны скорости и ускорения двух точек, то скорость и ускорение любой третьей точки этого же звена можно найти по подобию;

— имея план скоростей, можно найти угловую скорость любого звена механизма. Для определения угловой скорости исследуемого звена надо взять относительную скорость двух любых точек данного звена и разделить на расстояние между этими точками на механизме;

— имея план ускорений, можно найти угловое ускорение любого звена механизма. Для определения углового ускорения исследуемого звена надо взять тангенциальную составляющую относительного ускорения двух любых точек данного звена и разделить на расстояние между этими точками на механизме;

— звенья, соединенные в поступательную кинематическую пару, имеют одинаковые угловые скорости и одинаковые угловые ускорения.

При кинематическом исследовании плоских механизмов методом планов скоростей и ускорений встречается два случая:

1) две точки (одна исследуемая, вторая с известным законом движения, которое принимается в качестве переносного) принадлежат одному и тому же жесткому звену (рисунок 13).

В данном случае относительное движение этих точек получается за счет вращательного движения звена, на котором они находятся. При определении ускорений относительное ускорение раскладывается на нормальное (известное из физики как центростремительное – стремящееся к центру вращения) и тангенциальное.

2) звенья соединяются поступательной парой. В этом случае рассматриваются две точки, совпадающие в данный момент времени по своему положению, но принадлежащие разным звеньям – одна ползуну, другая направляющей

Если известен закон движения направляющей 1, то известны характеристики движения любой точки на этом звене, в том числе и точки С₁, принадлежащей этой направляющей.

Движение точки С₁ принимается в качестве переносного. Движение точки С₂, принадлежащей ползуну, относительно точки С₁ получается за счет поступательного движения ползуна вдоль направляющей (влияние вращательного движения исключается, т.к. радиус вращения равен нулю – положение точек С₁ и С₂ совпадает). При определении ускорений кроме относительного ускорения, направленного вдоль направляющей, возникает кориолисово ускорение (см. рисунок 14).

Исследование кинематики механизма методом планов начинается с начального механизма (с входного звена) и далее ведется по группам Ассура в порядке их присоединения к механизму. Для каждой группы Ассура разработаны методы решения (уравнения и порядок построения планов), которые являются неизменными, независимо от того, в каком механизме данная группа Ассура находится.

Источник

Степень подвижности механизма. Формула Сомова-Малышева для кинематической цепи общего вида

Степенью подвижности механизма называется число степеней свободы механизма относительно неподвижного звена (стойки).

Формула Сомова-Малышева для кинематической цепи общего вида:

где n – число подвижных звеньев кинематической цепи. Данное уравнение носит название структурной формулы кинематической цепи общего вида.

Степень подвижности механизма. Формула Чебышева для плоского механизма.

Степенью подвижности механизма называется число степеней свободы механизма относительно неподвижного звена (стойки).

Степень подвижности плоского механизма (все звенья движутся в параллельных плоскостях) определяется по формуле П.Л. Чебышева

где n – число подвижных звеньев; P5 – число КП 5-го класса; P4 – число КП 4-го класса.

Образование плоских механизмов путем наслоения структурных групп. Классификация групп Ассура. Схемы элементарных механизмов: шарнирного четырёхзвенника, кривошипно-ползунного, кривошипно-кулисного.

Следовательно, в структурную группу может входить только четное число звеньев, поскольку P5 может быть только целым числом.

Структурные группы различают по классу и порядку. Группа 2-го класса и 2-го порядка состоит из двух звеньев и трех КП. Класс группы (выше 2-го) определяется числом внутренних КП, образующих подвижный замкнутый контур из наибольшего числа звеньев группы.

Порядок группы определяется числом свободных элементов звеньев, которыми группа присоединяется к механизму.

25. Зубчатые механизмы. Опpеделение аксоиды, центpоиды. Виды зубчатых механизмов

Зубчатые механизмы – передаточные механизмы, содержащие, по крайней мере, одно зубчатое зацепление. Они передают вращение от одного вала другому и изменяют модуль и направление угловой скорости. Их называют также зубчатыми передачами, где с изменениями угловой скорости одновременно меняется и вращающий момент на ведомых валах. Давление зубьев вращающегося ведущего колеса передается зубьям ведомого колеса, при этом осуществляется его вращение. Зубчатые механизмы, в которых происходит уменьшение угловых скоростей при передаче движения от входного звена к выходному, называют понижающими передачами или редукторами. Зубчатые механизмы, в которых увеличиваются угловые скорости, называют повышающими передачами или мультипликаторами

По кинематическомупризнаку различают зубчатыемеханизмы с неподвижными осями всех колес (рядовые передачи) и механизмы, оси отдельных колес которых перемещаются относительно стойки. Такие механизмы называют планетарными и дифференциально-планетарными (зубчатыми дифференциалами)..

По расположению зубьев бывают: прямозубые, косозубые и шевронные.

По конструктивному оформлению различают зубчатые передачи:
— открытые, т. е. не заключенные в непроницаемый корпус и подверженные действию пыли и грязи;- закрытые, т. е. размещенные в специальном корпусе

Зубчатые механизмы относятся к разряду центроидных механизмов, в основе образования которых лежит центроида. Из теоретической механики известно, что мгновенное плоское движение твердого тела можно привести к одному мгновенному вращению вокруг оси, точка пересечения которой с плоскостью сечения твердого тела называется мгновенным центром вращения (МЦС). При непрерывном движении твердого тела мгновенная ось вращения описывает линейчатую поверхность (цилиндр), называемую аксоидом. В зависимости от того, к какой системе отсчета (неподвижной или движущейся вместе с телом) отнесена мгновенная ось вращения, получаются различные поверхности. Поэтому различают подвижный и неподвижный аксоиды. Аксоиды пересекаются с плоскостью сечения твердого тела по двум кривым, называемым центроидами.

Источник

Для чего применяется формула чебышева

Существует 5 классов кинематических пар.

Примеры различных КП смотри рис. 4-95.

Рис. 4-95. Классификация кинематических пар

Кинематические пары по характеру контакта звеньев, образующих КП, разделяют на :

Контакт звеньев в низшей КП осуществляется по поверхности. Контакт звеньев в высшей КП осуществляется либо по линии, либо в точке.

1.2 Определение числа степеней свободы рычажных механизмов.

В плоском механизме все звенья движутся в одной плоскости, все оси параллельны друг другу и перпендикулярны плоскости механизма.

Где n – число подвижных звеньев механизма, р_н – число низших КП, р_в – число высших КП.

n=3

1.2.2 Пространственные механизмы.

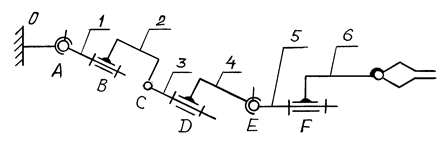
Допустим, что механизм, изображенный на рис.1.2.1 – пространственный и все кинематические пары 5-го класса, т.е. одноподвижны A_V,B_V,C_V,D_V, тогда

Для получения W _действ=1, необходимо добавить 3 движения.

Для того чтобы их устранить, надо изменить класс некоторых кинематических пар, при этом нельзя изменять класс КП А, чтобы задать входному звену 1 вполне определенное движение. Поэтому, сделаем КП В – сферическим шарниром, т.е. 3-го класса (добавим 2 подвижности), а КП С – 4-го класса (добавим 1 подвижность). Тогда

ФОРМУЛА СОМОВА-МАЛЫШЕВА: — является обобщающей формулой для определения числа степеней свободы

1.3 Кинематический анализ рычажных механизмов.

1.3.1 Основные понятия и определения.

полная скорость т. С будет

Вторая производная угловой функции положения звена по обобщенной координате – аналог углового ускорения звена в проекциях на соответствующие оси координат.

2. Аналитический способ определения кинематических параметров рычажных механизмов.

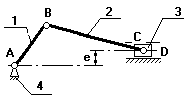
При исследования плоских рычажных механизмов для решения данной задачи целесообразно использовать метод проецирования векторного контура на оси координат.

Условие замкнутости векторного контура:

C проецируем данный векторный контур на оси X и Y.

(2)- проекция на ось X

(3)- проекция на ось Y

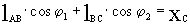
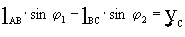
т.к. y_c=0, то из последнего уравнения следует

Источник

NB 3.1. Обобщенная координата механизма — одна или несколько угловых или линейных координат звеньев механизма.

Число обобщенных координат равно числу степеней свободы механизма, так как оно показывает, сколько независимых параметров может быть произвольно задано.

Существуют общие закономерности в структуре (строении) различных механизмов, связывающие число степеней свободы механизма с числом звеньев и числом и видом его кинематических пар. Эти закономерности носят название структурных формул кинематической цепи.

Вывод таких формул несложен. Общее число независимых движений n звеньев пространственного механизма равно 6n. Соединение звеньев в кинематические пары накладывает различное число связей (S = 1…5), которое необходимо исключить из 6n степеней свободы. Если число одноподвижных кинематических пар p₁, то общее число связей 5p₁, так как каждая пара имеет 5 связей. Для двухподвижных пар общее число связей 4p₂ и т.д., для пятиподвижных пар общее число связей 1p₅. Таким образом, число степеней свободы

W = 6n – 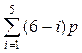_i.

Формула (3.1) называется структурной формулой кинематической цепи общего вида. Впервые она была дана в 1887 г. П.И. Сомовым и развита в 1923 г. А.П. Малышевым и носит название формулы Малышева. Следует обратить внимание на то, что в формуле Малышева сумма коэффициентов и индексов равна 6.

Пример 3.1. Рассчитать число степеней свободы механизма манипулятора (рис. 3.1).

Вычерчиваем кинематическую схему механизма. Заданная кинематическая цепь — пространственная незамкнутая. Обозначим характерные точки механизма буквами, номера звеньев — цифрами (стойка обозначается цифрой 0). Составляем таблицу пар и звеньев (табл. 3.1).

Источник