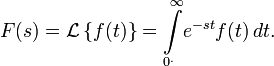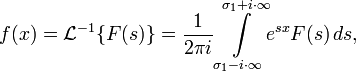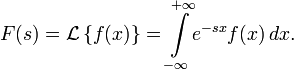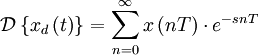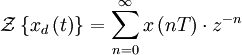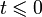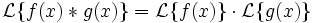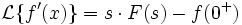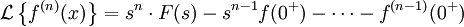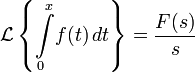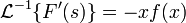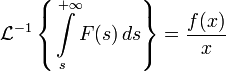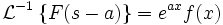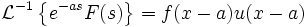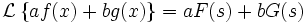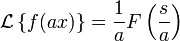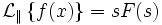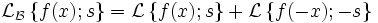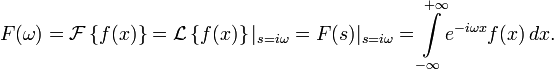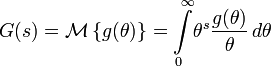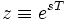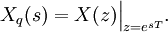Для чего применяется преобразование лапласа
Лапласа преобразование
Преобразова́ние Лапла́са — интегральное преобразование, связывающее функцию 
комплексного переменного (изображение) с функцией 
действительного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются дифференциальные и интегральные уравнения.
Одной из особенностей преобразования Лапласа, которые предопределили его широкое распространение в научных и инженерных расчётах, является то, что многим соотношениям и операциям над оригиналами соответствуют более простые соотношения над их изображениями. Так свёртка двух функций сводится в пространстве изображений к операции умножения, а линейные дифференциальные уравнения становятся алгебраическими.
Содержание
Определение
Прямое преобразование Лапласа
Преобразованием Лапласа функции действительной переменной , называется функция комплексной переменной 
, такая что:
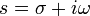
Правая часть этого выражения называется интегралом Лапласа.
Обратное преобразование Лапласа
Обратным преобразованием Лапласа функции комплексного переменного , называется функция действительного переменного, такая что:
где 
— некоторое вещественное число (см. условия существования). Правая часть этого выражения называется интегралом Бромвича.
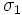
Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа — обобщение на случай задач, в которых для функции участвуют значения x
Двусторонее преобразование Лапласа определяется следующим образом:
Дискретное преобразование Лапласа
Применяется в сфере систем компьютерного управления. Дискретное преобразование Лапласа может быть применено для решётчатых функций.
Различают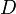 
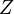
-преобразование и 
-преобразование.
Пусть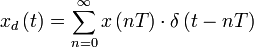 
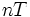
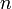
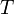
— решётчатая функция, то есть значения этой функции определены только в дискретные моменты времени 
, где 
— целое число, а 
— период дискретизации.
Тогда применяя преобразование Лапласа получим: 
Если применить следующую замену переменных: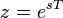 
,
получим Z-преобразование: 
Свойства и теоремы
,
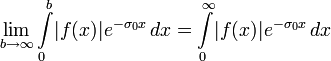
Преобразование Лапласа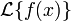 
существует в смысле абсолютной сходимости в следующих случаях:
Примечание: это достаточные условия существования.
Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:
1. Если изображение F(s) — аналитичная функция для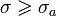 
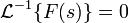
и имеет порядок меньше −1, то обратное преобразование для неё существует и непрерывно для всех значений аргумента, причём 
для 
2. Пусть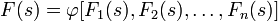 
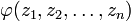
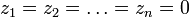
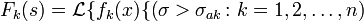
, так что 
аналитична относительно каждого zk и равна нулю для 
, и 
, тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.
Примечание: это достаточные условия существования.
Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов.
Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.
Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа.
Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала деленное на свой аргумент.
Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком.
Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, деленный на свой аргумент.
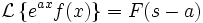
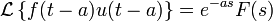
Теоремы о начальном и конечном значении (предельные теоремы):
, все полюсы в левой полуплоскости
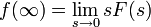
Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, к примеру, используется для анализа устойчивости траектории динамической системы.
Умножение на число
Прямое и обратное преобразование Лапласа некоторых функций
Ниже представлена таблица преобразования Лапласа для некоторых функций.
Применения преобразования Лапласа
Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники.
Связь с другими преобразованиями
Фундаментальные связи
Практически все интегральные преобразования имеют схожую природу и могут получаться одно из другого через выражения соответствия. Многие из них являются частными случаями других преобразований. Далее даны формулы, связывающие преобразования Лапласа с некоторыми другими функциональными преобразованиями.
Преобразование Лапласа-Карсона
Преобразование Лапласа-Карсона получается из преобразования Лапласа путём домножения его на комплексную переменную.
Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа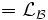 
связано с односторонним с помощью следующей формулы:
Преобразование Фурье
Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом s = iω :
Примечание: в этих выражениях опущен масштабирующий множитель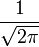 
, который часто включается в определения преобразования Фурье.
Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.
Преобразование Меллина
Преобразование Меллина и обратное преобразование Меллина связаны с двусторонним преобразованием Лапласа простой заменой переменных. Если в преобразовании Меллина
Z-преобразование
Z-преобразование — это преобразование Лапласа решётчатой функции, производимое с помощью замены переменных:
где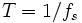 
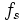
— период дискретизации, а 
— частота дискретизации сигнала. Связь выражается с помощью следующего соотношения:
Преобразование Бореля
Интегральная форма преобразования Бореля идентична преобразованию Лапласа, существует также обобщённое преобразование Бореля, с помощью которого использование преобразования Лапласа распространяется на более широкий класс функций.
Библиография
См. также
Внешние ссылки
Преобразование Абеля | Преобразования Бесселя | Преобразование Бушмана | Преобразование Гильберта | Преобразование Конторовича — Лебедева | Преобразование Лапласа | Преобразование Мейера | Преобразование Мелера — Фока | Преобразование Меллина | Преобразование Нерейна | Преобразование Радона | Преобразование Стильтьеса | Преобразование Фурье | Преобразование Хартли | Преобразование Хенкеля
Полезное
Смотреть что такое «Лапласа преобразование» в других словарях:
Лапласа преобразование — преобразование, переводящее функцию f (t) действительного переменного t (0 Большая советская энциклопедия
ЛАПЛАСА ПРЕОБРАЗОВАНИЕ — трансформация Лапласа, в широком смысле интеграл Лапласа вида где интегрирование производится по нек рому контуру Lв плоскости комплексного переменного z, ставящий в соответствие функции f(z). определенной на L, аналитич. функцию… … Математическая энциклопедия
ЛАПЛАСА ПРЕОБРАЗОВАНИЕ — в геометрии переход от одной фокальной сети конгруэнции к другой фокальной сети той же конгруэнции. Понятие Л. п. сети ввел Г. Дарбу (G. Darboux, 1888), обнаруживший, что аналитич. реобразование решений уравнения Лапласа где а, b, с известные… … Математическая энциклопедия
Преобразование Фурье — Преобразование Фурье операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие … … Википедия
Преобразование Радона — интегральное преобразование функции многих переменных, родственное преобразованию Фурье. Впервые введено в работе австрийского математика Иоганна Радона 1917 го года[1]. Важнейшее свойство преобразования Радона обратимость, то есть возможность… … Википедия
Преобразование Гегенбауэра — Преобразование Гегенбауэра интегральное преобразование функции : где многочлены Гегенбауэра. Если функция разлагается в обобщенный ряд Фурье по многочленам Гегенбауэра, то им … Википедия
Преобразование Лапласа — Преобразование Лапласа интегральное преобразование, связывающее функцию комплексного переменного (изображение) с функцией вещественного переменного (оригинал). С его помощью исследуются свойства динамических систем и решаются… … Википедия
Преобразование — одно из основных понятий математики, возникающее при изучении соответствий между классами геометрических объектов, классами функций и т.п. Например, при геометрических исследованиях часто приходится изменять все размеры фигур в одном и… … Большая советская энциклопедия
Преобразование Хенкеля — В математике, преобразование Ханкеля порядка ν функции f(r) задаётся формулой: где Jν функция Бесселя первого рода порядка ν и ν ≥ −1/2. Обратным преобразованием Ханкеля функции Fν(k) называют следующее выражение: которое можно проверить с… … Википедия
Преобразованное определение Лапласа, история, для чего оно, свойства
трансформируется из Лапласа В последние годы большое значение в исследованиях инженерии, математики, физики, а также в других научных областях, а также большой интерес к теоретическим вопросам, предоставляет простой способ решения проблем, возникающих в науке и технике..
Первоначально преобразование Лапласа было представлено Пьером-Саймоном Лапласом в его исследовании теории вероятностей и первоначально рассматривалось как математический объект, представляющий чисто теоретический интерес.
Современные приложения возникают, когда различные математики пытались дать формальное обоснование «эксплуатационным правилам», используемым Хевисайдом при изучении уравнений электромагнитной теории..
определение
Говорят, что преобразование Лапласа существует, если предыдущий интеграл сходится, иначе говорят, что преобразование Лапласа не существует.
В общем, для обозначения функции, которую нужно преобразовать, используются строчные буквы, а заглавная буква соответствует ее преобразованию. Таким образом, мы будем иметь:
примеров
Рассмотрим постоянную функцию f (t) = 1. Мы имеем ее преобразование:
Преобразование может существовать или не существовать, например, для функции f (t) = 1 / t интеграл, определяющий его преобразование Лапласа, не сходится и, следовательно, его преобразование не существует..
Достаточные условия для гарантии того, что преобразование Лапласа функции f существует, состоит в том, что f непрерывна по частям при t ≥ 0 и имеет экспоненциальный порядок.
Говорят, что функция непрерывна по частям при t ≥ 0, когда для любого интервала [a, b] с a> 0 существует конечное число точек tК, где f имеет разрывы и непрерывен в каждом подинтервале [tK-1,TК].
С другой стороны, говорят, что функция имеет экспоненциальный порядок c, если существуют действительные постоянные M> 0, c и T> 0, такие что:
В качестве примеров мы имеем, что f (t) = t 2 имеет экспоненциальный порядок, так как | t 2 | 3т для всех t> 0.
Формально мы имеем следующую теорему
Теорема (Достаточные условия существования)
Важно подчеркнуть, что это условие достаточности, то есть это может быть случай, когда существует функция, которая не удовлетворяет этим условиям, и даже тогда существует ее преобразование Лапласа..
Преобразование Лапласа некоторых основных функций
В следующей таблице приведены преобразования Лапласа наиболее распространенных функций.
история
Преобразование Лапласа обязано своим именем Пьеру-Симону Лапласу, математику и французскому астроному-теоретику, который родился в 1749 году и умер в 1827 году. Его слава была такова, что он был известен как Ньютон Франции.
В 1744 году Леонард Эйлер посвятил свои исследования интегралам с формой
как решения обыкновенных дифференциальных уравнений, но быстро отказались от этого исследования. Позже Джозеф Луи Лагранж, который очень восхищался Эйлером, также исследовал этот тип интегралов и связал их с теорией вероятностей..
1782, Лаплас
В 1782 году Лаплас начал изучать эти интегралы как решения дифференциальных уравнений, и, по мнению историков, в 1785 году он решил переформулировать проблему, которая позже породила преобразования Лапласа, как они понимаются сегодня..
Будучи введенным в области теории вероятностей, он не представлял большого интереса для ученых того времени и рассматривался только как математический объект, представляющий только теоретический интерес..
Оливер Хевисайд
В середине девятнадцатого века английский инженер Оливер Хевисайд обнаружил, что дифференциальные операторы можно рассматривать как алгебраические переменные, что дает их современное применение к преобразованиям Лапласа..
Оливер Хевисайд был английским физиком, инженером-электриком и математиком, который родился в 1850 году в Лондоне и умер в 1925 году. Пытаясь решать задачи дифференциальных уравнений, применяемых в теории вибраций и используя исследования Лапласа, он начал формировать современные применения преобразований Лапласа.
Результаты, представленные Хевисайдом, быстро распространились по всему научному сообществу того времени, но поскольку его работа не была строгой, его быстро раскритиковали более традиционные математики..
Однако полезность работы Хевисайда по решению уравнений физики сделала его методы популярными среди физиков и инженеров..
Несмотря на эти неудачи и после нескольких десятилетий неудачных попыток, в начале 20-го века можно было дать строгое обоснование эксплуатационным правилам, данным Хевисайдом..
Эти попытки окупились благодаря усилиям различных математиков, таких как Бромвич, Карсон, Ван дер Пол и другие..
свойства
Среди свойств преобразования Лапласа выделяются следующие:
линейность
В связи с этим свойством говорят, что преобразование Лапласа является линейным оператором.
пример
Первая теорема о переводе
Если это случится так:
пример
Поскольку преобразование Лапласа cos (2t) = s / (s ^ 2 + 4), то:
Вторая переводная теорема
пример
Если f (t) = t ^ 3, то F (s) = 6 / s ^ 4. И, следовательно, преобразование
Изменение масштаба
И «а» является ненулевым вещественным, мы должны
пример
Поскольку преобразование f (t) = sin (t) равно F (s) = 1 / (s ^ 2 + 1), оно должно быть
преобразование Лапласа производных
Преобразование Лапласа интегралов
Умножение на т N
Деление на т
Периодические функции
Пусть f периодическая функция с периодом T> 0, то есть f (t + T) = f (t), тогда
Поведение F (s), когда s стремится к бесконечности
Если f непрерывно по частям и экспоненциального порядка и
Обратные преобразования
Когда мы применяем преобразование Лапласа к функции f (t), мы получаем F (s), который представляет это преобразование. Таким же образом мы можем сказать, что f (t) является обратным преобразованием Лапласа F (s) и записывается как
Мы знаем, что преобразования Лапласа для f (t) = 1 и g (t) = t равны F (s) = 1 / s и G (s) = 1 / s 2 соответственно, поэтому мы должны
Некоторые общие обратные преобразования Лапласа следующие
Кроме того, обратное преобразование Лапласа является линейным, то есть выполняется
осуществление
Чтобы решить это упражнение, мы должны сопоставить функцию F (s) с одной из предыдущих таблиц. В этом случае, если мы берем n + 1 = 5 и используем свойство линейности обратного преобразования, мы умножаем и делим на 4! получение
Для второго обратного преобразования мы применяем частичные дроби, чтобы переписать функцию F (s), а затем свойство линейности, получая
Как мы видим из этих примеров, общепринято, что оцениваемая функция F (s) не совсем совпадает ни с одной из функций, приведенных в таблице. Для этих случаев, как это наблюдается, достаточно переписать функцию до достижения соответствующей формы.
Применение преобразования Лапласа
Дифференциальные уравнения
Используя свойство преобразования производной ясно, что
И из n-1 производных, оцененных при t = 0.
Это свойство делает преобразование очень полезным для решения начальных задач, в которых используются дифференциальные уравнения с постоянными коэффициентами..
Следующие примеры показывают, как использовать преобразование Лапласа для решения дифференциальных уравнений.
Пример 1
Учитывая следующую начальную задачу
Используйте преобразование Лапласа, чтобы найти решение.
Мы применяем преобразование Лапласа к каждому члену дифференциального уравнения
Для свойства преобразования производной имеем
Развивая все выражения и убирая А (и), мы остаемся
Используя частичные дроби, чтобы переписать правую часть уравнения, мы получим
Пример 2
Как и в предыдущем случае, мы применяем преобразование с обеих сторон уравнения и разделяем член на член.
Таким образом, мы имеем в результате
Подстановка с заданными начальными значениями и очистка Y (s)
Используя простые дроби, мы можем переписать уравнение следующим образом
И применение обратного преобразования Лапласа дает нам в результате
В этих примерах можно прийти к неверному выводу, что этот метод не намного лучше традиционных методов решения дифференциальных уравнений..
Преимущества, предлагаемые преобразованием Лапласа, заключаются в том, что нет необходимости использовать изменение параметров или беспокоиться о различных случаях метода неопределенных коэффициентов.
Помимо решения задач начального значения этим методом, с самого начала мы используем начальные условия, поэтому нет необходимости выполнять другие расчеты, чтобы найти конкретное решение..
Системы дифференциальных уравнений
Преобразование Лапласа также можно использовать для поиска решений одновременных обыкновенных дифференциальных уравнений, как показано в следующем примере..
пример
При начальных условиях x (0) = 8 e и (0) = 3.
Разрешение результатов в нас
И при применении обратного преобразования Лапласа мы имеем
Механика и электрические цепи
Преобразование Лапласа имеет большое значение в физике, в основном имеет применение для механических и электрических цепей.
Простая электрическая схема состоит из следующих элементов
Переключатель, батарея или источник, индуктор, резистор и конденсатор. Когда переключатель замкнут, вырабатывается электрический ток, который обозначается как i (t). Заряд конденсатора обозначается через q (t).
По второму закону Кирхгофа напряжение, создаваемое источником E для замкнутой цепи, должно быть равно сумме каждого падения напряжения.
Электрический ток i (t) связан с зарядом q (t) в конденсаторе как i = dq / dt. С другой стороны, падение напряжения определяется в каждом из элементов следующим образом:
Падение напряжения на резисторе равно iR = R (дк / дт)
Падение напряжения в индуктивности составляет L (di / dt) = L (d 2 д / д 2 )
Падение напряжения в конденсаторе составляет q / C
С этими данными и применением второго закона Кирхгофа к замкнутой простой схеме получается дифференциальное уравнение второго порядка, которое описывает систему и позволяет нам определить значение q (t)..
пример
Индуктор, конденсатор и резистор подключены к батарее E, как показано на рисунке. Индуктор имеет 2 Генри, конденсатор 0,02 Фарад и сопротивление 16 Ом. В момент времени t = 0 цепь замкнута. Найти нагрузку и ток в любой момент времени t> 0, если E = 300 вольт.
У нас есть то, что дифференциальное уравнение, которое описывает эту схему, является следующим
Если начальные условия q (0) = 0, i (0) = 0 = q ‘(0).
Применяя преобразование Лапласа, мы получаем, что
Затем, применяя обратное преобразование Лапласа, мы имеем