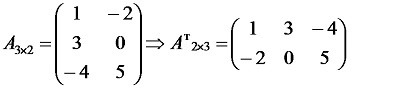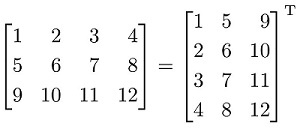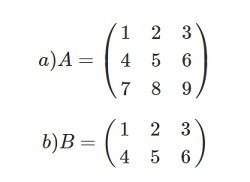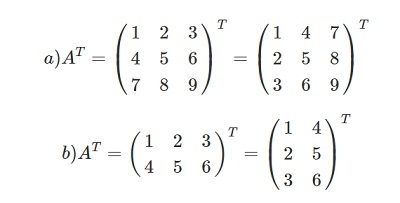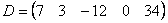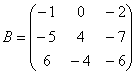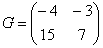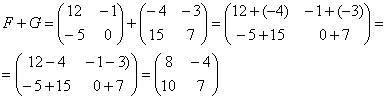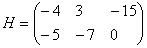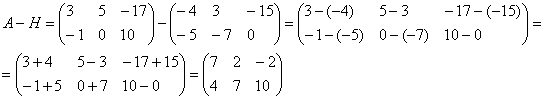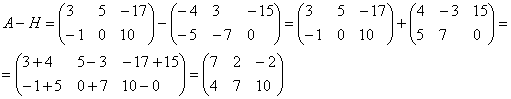Для чего транспортируют матрицу

Транспонирование матрицы

Обновлено: 19 Июля 2021

Нам уже знакомо понятие матрицы. Этот математический объект имеет прикладное значение: он позволяет структурировать числа и информацию, проводить сложные расчёты. С ним можно проделывать различные операции, и одной из них является транспортирование.

Что такое транспонированная матрица, в чем отличие от обычной

Транспонирование – это алгоритм, при котором m-строки меняются местами с n-столбцами.

Транспонированная матрица, в отличие от обычной, помогает получить одинаковый результат при умножении на вектор-столбец и вектор-строку, что значительно упрощает дальнейшие математические вычисления.

Особенности, определитель и свойства целочисленных

Свойства транспортирования целочисленных матриц:

Если матрица А – квадратная (m=n), то определитель исходной и транспортированной матрицы равны: det A T = det A.

Напомним, что определитель – это некоторое число, с которым можно сравнить любую квадратную матрицу.

Формула, как обозначается транспонированная матрица

Тогда формула для транспортировки выглядит следующим образом:

A T ij = A ji

Формально, если А = m × n, то A T = n × m, но математически это записывается через индексы i и j.

Примеры задач на транспонирование матриц

Само транспортирование – довольно лёгкий процесс. Рассмотрим один пример.

Задача: даны А = (m × n) и В = (m × n).

Необходимо выполнить транспортирование.

Произведение и сумма транспонированных матриц

Теорема: транспонирование произведения матриц равно произведению транспонированных матриц, взятых в обратном порядке.

В математическом виде теорема выглядит так:

С T = (A · B) T = В T · А T

Сумма вычисляется по аналогичной формуле:

C T = (A + B) T = A T + В T

Периодически возникают сложности с учебой? ФениксХэлп может помочь!

Источник

Транспонирование матрицы, умножение, возведение в степень

Как мы выяснили в предыдущей статье, с матрицами можно выполнять различные простые операции, такие как сложение, вычитание, умножение и т.д. Они называются простыми, поскольку имеют аналогии с операциями над обычными числами.

Но существуют и такие операции как транспонирование матрицы, произведение двух матриц и возведение матрицы в степень. Они уже имеют свой уникальный алгоритм действий, который мы сейчас разберем.

Итак, приступим к практике.

1. Транспонирование матрицы

Простым языком – это переворачивание матрицы, то есть первая строка превращается в первый столбец, вторая строка превращается во второй столбец, третья строка превращается в третий столбец и так далее.

Пусть дана матрица размером 4×3:

2. Произведение матриц

Рассмотрим такое произведение матриц:

ВАЖНО! Матрицы должны быть согласованными, то есть число столбцов в первой матрице А_{3х 3} должно совпадать с числом строк во второй матрице B _{3 х2}. Если этого не происходит, значит провести умножение матриц невозможно.

2.1. Первым делом нам необходимо выяснить размер матрицы C. Для этого мы берем количество строк А_{3х 3} и количество столбцов B _{3 х2} и получаем, что матрица будет состоять из 3 строк на 2 столбцов.

2.2. Далее необходимо вычислить каждый элемент матрицы C. Для этого мы обращаем внимание на индекс каждого элемента. Первый индекс числа c _{1 1} отвечает за номер строки в первой матрице, а второй индекс (c_{1 1} ) отвечает за номер столбца во второй матрице.

Исходя из этой информации, необходимо вычислить сумму произведений всех элементов в соответствующих сроках и столбцах.

2.3. Аналогично получаем остальные элементы:

Необходимо помнить ПРАВИЛО, что A*B≠B*A. Это равенство будет выполняться только в том случае, если матрицы A и B являются перестановочными.

3. Возведение матрицы в степень

Для этого необходимо умножать матрицу на саму себя то число раз, которое указано в степени.

Теперь произведем вычисления:

Умножение происходит по алгоритму, описанному выше.

Можно заметить, что количество вычислений становится все больше и больше, поэтому советуем всегда перепроверять полученный результат.

Источник

Иллюстрированный самоучитель по MathCAD 11

Простейшие операции с матрицами. Транспортирование.

Простейшие операции матричной алгебры реализованы в Mathcad в виде операторов. Написание операторов по смыслу максимально приближено к их математическому действию. Каждый оператор выражается соответствующим символом Рассмотрим матричные и векторные операции Mathcad 11. Векторы являются частным случаем матриц размерности NXI, поэтому для них справедливы все те операции, что и для матриц, если ограничения особо не оговорены (например некоторые операции применимы только к квадратным матрицам NXN). Какие-то действия допустимы только для векторов (например скалярное произведение), а какие-то, несмотря на одинаковое написание, по-разному действуют на векторы и матрицы.

Непосредственное проведение векторных операций над строками, т. е. матрицами IXN, невозможно, для того чтобы превратить строку в вектор, ее нужно предварительно транспонировать.

Рис. 9.1. Панель инструментов Matrix

Транспортирование

Транспортированием называют операцию, переводящую матрицу размерности MXN в матрицу размерности NXM, делая столбцы исходной матрицы строками, а строки – столбцами. Пример приведен в листинге 9.1. Ввод символа транспонирования (transpose) осуществляется с помощью панели инструментов Matrix (Матрица) или нажатием клавиш CTRL + 1. Не забывайте, что для вставки символа транспонирования матрица должна находиться между линиями ввода.

Листинг 9.1. Транспонирование векторов и матриц:

Источник

Для чего транспортируют матрицу

Для того чтобы транспонировать матрицу, нужно ее строки записать в столбцы транспонированной матрицы.

Транспонировать матрицу

Строка здесь всего одна и, согласно правилу, её нужно записать в столбец:

– транспонированная матрица.

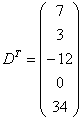
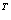
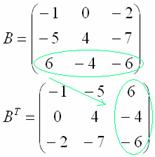
Транспонированная матрица обычно обозначается надстрочным индексом или штрихом справа вверху.

Транспонировать матрицу

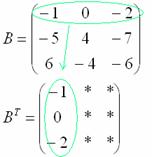
Сначала переписываем первую строку в первый столбец:

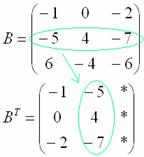
Потом переписываем вторую строку во второй столбец:

И, наконец, переписываем третью строку в третий столбец:

Готово. Грубо говоря, транспонировать – это значит повернуть матрицу набок.

4) Действие четвертое. Сумма (разность) матриц.

Сумма матриц действие несложное.
НЕ ВСЕ МАТРИЦЫ МОЖНО СКЛАДЫВАТЬ. Для выполнения сложения (вычитания) матриц, необходимо, чтобы они были ОДИНАКОВЫМИ ПО РАЗМЕРУ.

Например, если дана матрица «два на два», то ее можно складывать только с матрицей «два на два» и никакой другой!

Сложить матрицы 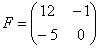и

Для того чтобы сложить матрицы, необходимо сложить их соответствующие элементы:

Для разности матриц правило аналогичное, необходимо найти разность соответствующих элементов.

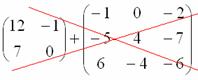
Найти разность матриц ,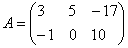

А как решить данный пример проще, чтобы не запутаться? Целесообразно избавиться от лишних минусов, для этого внесем минус в матрицу :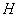

Примечание: в теории высшей математики школьного понятия «вычитание» нет. Вместо фразы «из этого вычесть это» всегда можно сказать «к этому прибавить отрицательное число». То есть, вычитание – это частный случай сложения.

Источник

Линейная алгебра на Python. [Урок 2]. Транспонирование Матрицы

В этом уроке мы рассмотрим операцию “транспонирование матрицы” и как она выполняется на Python. Также разберем на примерах свойства этой операции.

Транспонирование матрицы

Для исходной матрицы:

Транспонированная будет выглядеть так:

Транспонируем матрицу с помощью метода transpose():

Существует сокращенный вариант получения транспонированной матрицы, он очень удобен в практическом применении:

Рассмотрим на примерах свойства транспонированных матриц. Операции сложения и умножение матриц, а также расчет определителя более подробно будут рассмотрены в последующих уроках.

В данном примере, для умножения матриц, использовалась функция dot() из библиотеки Numpy.

Ввиду особенностей Python при работе с числами с плавающей точкой, в данном примере вычисления определителя рассматриваются только первые девять значащих цифр после запятой (за это отвечает параметр ‘.9g’ ).

P.S.

Источник