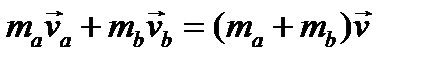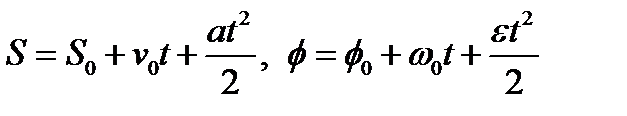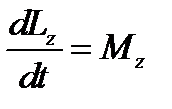Для чего в физике вводят систему отсчета приведите примеры
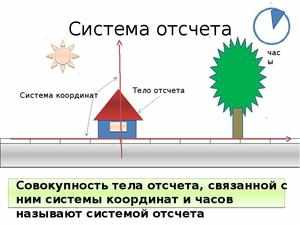
Система отсчёта в физике — что это, определение и виды

С точки зрения современной физики, всякое движение можно признать относительным. Таким образом, любое движение тела можно рассматривать исключительно по отношению к другому материальному объекту или же совокупности таких объектов. Например, мы не можем указать, каков характер движения Луны в общем, но может определить её перемещение относительно Солнца, Земли, Звёзд, других планет и пр.
В ряде случаев подобная закономерность бывает связана не с единой материальной точкой, а с множеством базовых точек отсчёта. Эти базовые тела отсчёта могут задавать совокупность координат.
Основные составляющие
Основными составляющими любой системы отсчёта в механике можно считать следующие компоненты:
Для того чтобы решить конкретную задачу, необходимо определить наиболее подходящую для этого сетку координат и структуру. Идеальные часы в каждой из них потребуются лишь одни. В этом случае начало, тело отсчёта и векторы координатных осей можно выбирать произвольно.
Основные свойства

Под однородностью в физике принято понимать тождественность всех точек в пространстве. Этот фактор имеет в физике немаловажное значение. Во всех точках Земли и Солнечной системы в целом законы Ньютона в физики действуют абсолютно идентично. Благодаря этому начало отсчёта может быть размещено в любой удобной точке. И если исследователь поворачивает сетку координат вокруг начальной точки, при этом никакие другие параметры задачи не будут изменяться. Все направления, которые начинаются от этой точки, имеют абсолютно тождественные свойства. Такая закономерность называется изотропностью пространства.
Виды систем отсчёта
Существует несколько видов — подвижные и неподвижные, инерциальные и неинерциальные.
Если такая совокупность координат и времени требуется для проведения кинематических исследований, в этом случае все подобные структуры являются равноправными. Если же речь идёт о решении динамических задач, предпочтение отдаётся инерциальным разновидностям – в них движение имеет более простые характеристики.
Инерциальные системы отсчёта
Инерциальными называют такие совокупности, в которых физическое тело сохраняет состояние покоя или продолжает равномерно передвигаться, если на него не воздействуют внешние силы или суммарное воздействие этих сил равняется нулю. В этом случае на тело действует инерция, что и даёт название системе.
Одна и та же совокупность в одном случае может считаться инерциальной, а в другом будет признана неинерциальной. Это происходит в тех случаях, когда погрешность в результате неинерциальности слишком ничтожна и ею можно свободно пренебречь.
Неинерциальные системы отсчёта
Отличительной чертой неинерциальной системы является то, что она перемещается по отношению к инерциальной с некоторым ускорением. В этом случае законы Ньютона могут утратить свою силу и требуют введения дополнительных переменных. Без этих переменных описание такой совокупности будет недостоверным.
Проще всего рассматривать неинерциальную систему на примере. Такая характеристика движения характерна для всех тел, которые имеют сложную траекторию движения. Наиболее ярким примером такой системы можно считать вращение планет, в том числе и Земли.
Движение в неинерциальных системах отсчёта впервые изучено Коперником. Именно он доказал, что движение с участием нескольких сил может быть весьма сложным. До этого считалось, что движение Земли относится к инерциальным и описывалось оно законами Ньютона.
Системы отсчета и их виды
В физике часто встречаются термины «система отсчета» и «инерциальная система отсчета». Ознакомимся с ними.
Что такое система отсчета
Система отсчета содержит:
Если все три пункта выполнены, то говорят, что задана система отсчета.
С телом отсчета связаны координатные оси, если тело отсчета будет двигаться, то система отсчета будет передвигаться совместно с ним.
Системы отсчета используются не только в физике. В повседневной жизни мы пользуемся картами местности. При этом, на карте мы отмечаем две точки:
Проложив маршрут и измерив расстояние между этими точками, мы сможем посчитать расстояние, которое нужно преодолеть, чтобы переместиться. А указав интервал времени, мы сможем рассчитать, с кокой скоростью нужно двигаться, чтобы вовремя прибыть к месту назначения.
Виды систем отсчета и их сравнение
Все системы отсчета (сокращенно СО) можно разделить на два вида:
От того, как система отсчета движется, зависит, можно ли считать ее инерциальной, или нет.
Инерциальные системы отсчета
Инерциальная система отсчета — это такая, которая:
Примеры инерциальных систем отсчета:
Примечания:
1. Вместо слов «скорость не меняется», физики часто употребляют такие слова: «скорость постоянная», или «модуль вектора скорости сохраняется».
2. Скорость – это вектор, у любого вектора есть две главные характеристики:
Подробнее о векторах и их характеристиках «здесь».
Не инерциальные системы отсчета
Не инерциальная система отсчета — это такая, которая:
Бывает и так, что одновременно изменяет и по модулю, и по направлению. Главное, что изменяет. Например, гоночный автомобиль на соревнованиях входит в поворот и одновременно набирает скорость.
Примеры не инерциальных систем отсчета:
Для чего нужно знать, к какому виду отнести систему отсчета
Предположим, нам нужно решить какую-то задачу механики. Чтобы ее решить мы вводим систему отсчета. Является ли система отсчета инерциальной, нужно знать потому, что
Для иллюстрации рассмотрим такой пример:
Представим, что мы находимся внутри пассажирского вагона. Поднимем на вытянутой руке мяч и разожмем ладонь, чтобы мяч из нее выпал. Будем изучать траекторию, по которой мяч движется. На всех рисунках пунктиром обозначено начальное положение мяча, а сплошным кругом — его конечное положение. Рассмотрим движение мяча в каждом из случаев:
Случай 1. Вагон покоится
Когда вагон покоится, свободно падающий мяч падает вертикально
Случай 2. Вагон движется равномерно прямолинейно
Красная стрелка — это вектор скорости вагона, он обозначен символом \( \vec
Когда вагон движется равномерно прямолинейно, свободно падающий мяч падает вертикально
Случай 3. Вагон движется прямолинейно равнозамедленно
Вектор скорости вагона обозначен символом \( \vec
Когда вагон движется прямолинейно равнозамедленно, свободно падающий мяч отклоняется от вертикали.
Случай 4. Вагон движется прямолинейно равноускоренно
Вектор скорости вагона \( \vec
Когда вагон движется прямолинейно равноускоренно, свободно падающий мяч отклоняется от вертикали
Случай 5. Вагон движется криволинейно
На рисунке представлена одна из возможных траекторий движения мяча. Траектория мяча будет зависеть от того, будет ли вагон, входящий в поворот, ускоряться, или замедляться.
Изогнутая стрелка указывает направление, в котором вагон поворачивает (изменяет направление движения).
Когда вагон движется криволинейно, свободно падающий мяч отклоняется от вертикали.
Подведем итог:
В первых двух случаях (см. рис. №1, №2), траектории мяча были одинаковыми. В этих двух случаях вагон является инерциальной системой отсчета.
Рисунки №3, №4 и №5 иллюстрируют неинерциальные системы отсчета. В случаях, представленных на этих рисунках, траектории мяча различаются. Формы траекторий зависят от дополнительных сил, действующих в неинерциальных системах отсчета на мяч.
Для чего в физике вводят систему отсчета приведите примеры
Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел.
Математически движение тела (или материальной точки) по отношению к выбранной системе отсчёта описывается уравнениями, которые устанавливают, как изменяются с течением времени t координаты, определяющие положение тела (точки) в этой системе отсчёта. Эти уравнения называются уравнениями движения. Например, в декартовых координатах х, y, z движение точки определяется уравнениями
Движущиеся тела изменяют своё положение относительно других тел в пространстве с течением времени. Положение автомобиля, мчащегося по шоссе, изменяется относительно указателей на километровых столбах, положение корабля, плывущего в море недалеко от берега, меняется относительно береговой линии, а о движении самолёта, летящего над землей, можно судить по изменению его положения относительно поверхности Земли. Можно показать, что одно и то же тело при одном и том же движении может одновременно по-разному перемещаться относительно разных тел.
Абсолютная система отсчёта
Часто в физике какую-то СО считают наиболее удобной (привилегированной) в рамках решения данной задачи — это определяется простотой расчётов либо записи уравнений динамики тел и полей в ней. Обычно такая возможность связана с симметрией задачи.
С другой стороны, ранее считалось, что существует некая «фундаментальная» система отсчёта, простота записи в которой законов природы выделяет её из всех остальных систем. Например, физики XIX в. считали что, система, относительно которой покоится эфир электродинамики Максвелла, является привилегированной, и поэтому она была названа Абсолютной Системой Отсчета (АСО). В современных представлениях никакой системы отсчёта, выделенной именно таким способом, не существует, так как законы природы, выраженные в тензорной форме, имеют один и тот же вид во всех системах отсчёта — то есть во всех точках пространства и во все моменты времени. Это условие — локальная пространственно-временная инвариантность — является одним из проверяемых оснований физики.
Иногда абсолютной системой отсчета называют систему, связанную с реликтовым излучением, то есть инерциальную систему отсчета, в которой реликтовое излучение не имеет дипольной анизотропии.
Ответынавопросыдлязащитылабораторнойработы№1 пофизике:3



1. Что такое система отсчета? Зачем вводится это понятие в физике? Приведите примеры.
Ответ:Система отсчета – совокупность системы координат и часов, связанных с телом отсчёта.
Система отсчета используется для задания положения тела (материальной точки), относительно других тел (м.т.), в дальнейшем необходимое для описания движения данного тела (м.т.).
2. Что такое система тел?
Ответ:Система тел – физическая система, состоящая из нескольких (взаимодействующих или не взаимодействующих) тел, движения и положения которых взаимосвязаны.
3. Что такое материальная точка? Что такое твердое тело? Приведите примеры.
Ответ:Материальная точка – тело, размерами которого в условиях данной задачи можно пренебречь (но не массой). Пример: небесное тело можно представить как м.т. при нахождении координат его положения относительно Земли.
Абсолютно твердое тело – совокупность материальных точек, расстояние между которыми с течением времени не меняется. Примером а.т.т. может быть любое тело, деформацией которого в конкретной задаче можно пренебречь. В природе а.т.т. не существует, т.к. все реальные тела подвержены деформации.
4. Как определяют положение материальной точки в векторном, координатном и естественном способах описания механического движения
 |
 |
 |
 |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA6qlORcUA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPT4vCMBTE7wv7HcJb8LamVhTpGkUKsiJ68M/F29vm 2Rabl24TtfrpjSB4HGbmN8x42ppKXKhxpWUFvW4EgjizuuRcwX43/x6BcB5ZY2WZFNzIwXTy+THG RNsrb+iy9bkIEHYJKii8rxMpXVaQQde1NXHwjrYx6INscqkbvAa4qWQcRUNpsOSwUGBNaUHZaXs2 CpbpfI2bv9iM7lX6uzrO6v/9YaBU56ud/YDw1Pp3+NVeaAVxH55fwg+QkwcAAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQDqqU5FxQAAANsAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA » filled=»f» stroked=»f» strokeweight=».5pt»>
 |
| O |
| Z |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA8O7jdMUA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE74L/YXlCb7qJxSLRVUJAWooetF68PbPP JJh9m2a3Sdpf3xUKPQ4z8w2z3g6mFh21rrKsIJ5FIIhzqysuFJw/dtMlCOeRNdaWScE3OdhuxqM1 Jtr2fKTu5AsRIOwSVFB63yRSurwkg25mG+Lg3Wxr0AfZFlK32Ae4qeU8il6kwYrDQokNZSXl99OX UfCe7Q54vM7N8qfOXve3tPk8XxZKPU2GdAXC0+D/w3/tN63gOYbHl/AD5OYXAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQDw7uN0xQAAANsAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA » filled=»f» stroked=»f» strokeweight=».5pt»>
| X |
| Y |
| x |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAN3ar5cUA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPT4vCMBTE7wt+h/AEb2uq64pUo0hBVsQ9+Ofi7dk8 22LzUpuo1U+/WRA8DjPzG2Yya0wpblS7wrKCXjcCQZxaXXCmYL9bfI5AOI+ssbRMCh7kYDZtfUww 1vbOG7ptfSYChF2MCnLvq1hKl+Zk0HVtRRy8k60N+iDrTOoa7wFuStmPoqE0WHBYyLGiJKf0vL0a Batk8YubY9+MnmXysz7Nq8v+8K1Up93MxyA8Nf4dfrWXWsHgC/6/hB8gp38AAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQA3dqvlxQAAANsAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA » filled=»f» stroked=»f» strokeweight=».5pt»>
| z |
| y |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEA19OWCsUA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE74X+h+UJvdWN0ohEVwkBaSn2oPXi7Zl9 JsHs2zS7TaK/3i0IPQ4z8w2zXA+mFh21rrKsYDKOQBDnVldcKDh8b17nIJxH1lhbJgVXcrBePT8t MdG25x11e1+IAGGXoILS+yaR0uUlGXRj2xAH72xbgz7ItpC6xT7ATS2nUTSTBisOCyU2lJWUX/a/ RsFntvnC3Wlq5rc6e9+e0+bncIyVehkN6QKEp8H/hx/tD63gLYa/L+EHyNUdAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQDX05YKxQAAANsAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA » filled=»f» stroked=»f» strokeweight=».5pt»>
 |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAQn2jT8IA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbERPTWvCQBC9F/wPywje6saARaKrSCBYxB5ivfQ2Zsck mJ2N2a2J/fXdg+Dx8b5Xm8E04k6dqy0rmE0jEMSF1TWXCk7f2fsChPPIGhvLpOBBDjbr0dsKE217 zul+9KUIIewSVFB53yZSuqIig25qW+LAXWxn0AfYlVJ32Idw08g4ij6kwZpDQ4UtpRUV1+OvUbBP sy/Mz7FZ/DXp7nDZtrfTz1ypyXjYLkF4GvxL/HR/agXzsD58CT9Arv8BAAD//wMAUEsBAi0AFAAG AAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54bWxQ SwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJlbHNQ SwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBleG1s LnhtbFBLAQItABQABgAIAAAAIQBCfaNPwgAAANsAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMvZG93 bnJldi54bWxQSwUGAAAAAAQABAD1AAAAhwMAAAAA » filled=»f» stroked=»f» strokeweight=».5pt»>
| А |
| О |
| S |
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEAsq89OMUA AADbAAAADwAAAGRycy9kb3ducmV2LnhtbESPQWvCQBSE74X+h+UJvdWNlohEVwkBaSn2oPXi7Zl9 JsHs2zS7TaK/3i0IPQ4z8w2zXA+mFh21rrKsYDKOQBDnVldcKDh8b17nIJxH1lhbJgVXcrBePT8t MdG25x11e1+IAGGXoILS+yaR0uUlGXRj2xAH72xbgz7ItpC6xT7ATS2nUTSTBisOCyU2lJWUX/a/ RsFntvnC3Wlq5rc6e9+e0+bncIyVehkN6QKEp8H/hx/tD60gfoO/L+EHyNUdAAD//wMAUEsBAi0A FAAGAAgAAAAhAPD3irv9AAAA4gEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5cGVzXS54 bWxQSwECLQAUAAYACAAAACEAMd1fYdIAAACPAQAACwAAAAAAAAAAAAAAAAAuAQAAX3JlbHMvLnJl bHNQSwECLQAUAAYACAAAACEAMy8FnkEAAAA5AAAAEAAAAAAAAAAAAAAAAAApAgAAZHJzL3NoYXBl eG1sLnhtbFBLAQItABQABgAIAAAAIQCyrz04xQAAANsAAAAPAAAAAAAAAAAAAAAAAJgCAABkcnMv ZG93bnJldi54bWxQSwUGAAAAAAQABAD1AAAAigMAAAAA » filled=»f» stroked=»f» strokeweight=».5pt»>
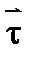 |
. Ответ:
Векторный способ: положение материальной точки задаётся с помощью радиуса вектора 




Координатный способ: с телом отсчёта связывают какую-либо систему координат (например, декартову).


Естественный способ: движение описывается с помощью параметров самой траектории, и он используется, когда траектория известна.



5. Как определяют изменение положения материальной точки в трех способах описания движения тел?
Ответ:В векторном способе при движении точки M в некоторой системе отсчета Oxyz вектор 
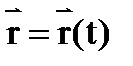

В координатном способе необходимо знать значение координат точки в каждый момент времени. Применяя закон движения м.т. в координатном виде мы можем найти числовые значения проекций радиус-вектора движущейся точки на координатные оси
В естественном способе выберем некоторую неподвижную точку O’, которую будем считать началом отсчёта, и определим положительное и отрицательное направление точки M, движущейся вдоль траектории AB. Тогда положение точки M будет определяться расстояниемS от точкиO’. При движении точка М переместиться в точку М’.
| O’ |
| B |
| M |
| M’ |
| s |
| A |
6. Дайте определение мгновенной скорости. Как направлен вектор мгновенной скорости? В каких единицах она измеряется?
Ответ:Мгновенная скорость – векторная величина, равная производной от радиуса-вектора по времени. Мгновенная скорость равна пределу отношения перемещения dr ко времени dt, за которое произошло перемещение, при dtстремящемся к нулю: 
Вектор мгновенной скорости направлен по касательной к траектории в сторону движения.
7. Как по графику зависимости координаты материальной точки от времени найти значение проекции средней скорости, проекции мгновенной скорости
8. Дайте определение мгновенного ускорения. Как направлен вектор ускорения? В каких единицах ускорение измеряется?
В случае движения в плоскости вектор ускорения можно разложить по сопутствующему базису: на вектор нормальногои тангенциальногоускорения:
Здесь 
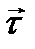



9. Раскройте физический смысл всех кинематических характеристик поступательного движения.
Ответ:Поступательное движение– движение, при котором прямая, проходящая через любые две точки тела, в процессе движения остаётся параллельной самой себе.
Кинематические характеристики поступательного движения: путь, перемещение, скорость, ускорение.
Путь 
Перемещение 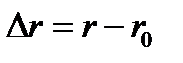
Скорость – скалярная физическая величина, характеризующая быстроту изменения координаты точки в пространстве.
Ускорение – вектор направленный вдоль вектора приращения скорости dv, модуль ускорения характеризует величину изменения скорости в единицу времени.
10. Сформулируйте первый закон Ньютона. Объясните, какие системы отсчёта называют инерциальными. Как определить, инерциальна ли конкретная система отсчета?
Ответ:Первый закон Ньютона – всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние.
Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называют инертностью.
Инерциальные системы отсчёта – системы отсчёта, по отношению к которым выполняется первый закон Ньютона.
Если относительно некоторой системы отсчета материальная точка свободна от внешних воздействий, либо покоится, либо движется равномерно, то эта система отсчета является инерциальной.
11. Что нужно для того, чтобы тело двигалось?
Ответ:Для того, чтобы тело двигалось равномерно или прямолинейно, никакие силы не нужны :D. А вообще, тело может покоиться в одной системе отсчета (шарик лежит на столе), но двигаться в другой системе отсчёта (стол стоит в вагоне поезда, который везет и шарик, и стол, значит шарик движется в системе отсчета Земли, но при этом шарик покоится в системе отсчета стола).
12. Что такое масса тела? В каких единицах она измеряется?
Ответ:Масса тела – физическая величина, являющаяся одной из основных характеристик материи, определяющая её инерционные (инертность) и гравитационные свойства (вес). В системе Си измеряется в кг.
13. Что такое импульс материальной точки? В каких единицах он измеряется?
Ответ:Импульс м.т. – векторная физическая величина, являющаяся мерой механического движения тела.В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости: 
В системе СИ импульс измеряется в кг*м/с.
14. Сформулируйте второй закон Ньютона. При каких условиях он выполняется?
Ответ:Второй закон Ньютона – основной закон динамики поступательного движения – отвечает на вопрос, как изменяется механическое движение материальной точки (тела) под действием приложенных к ней сил.
Второй закон Ньютона: ускорение, приобретаемое материальной точкой (телом), пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
Второй закон Ньютона (общ) – скорость изменения импульса материальной точки равна действующей на нее силе.
Второй закон Ньютона справедлив только для движения тел со скоростями, много меньшими скорости света.
15. К чему приводит воздействие силы на тело?
Ответ:Воздействие силы на тело приводят данное тело вдвижение. Зная силы, действующие на тело, можно предсказать как будет двигаться тело под действием этих сил, в какой момент времени тело окажется в нужной точке пространства (кроме сил необходимо также знать начальное положение тела и его начальную скорость.
16. Сформулируйте третий закон Ньютона. Поясните, может ли нарушаться этот закон для движущихся относительно друг друга тел в инерциальной системе отсчёта.
Ответ:Третий закон Ньютона рассматривает взаимодействие двух тел. Он гласит: силы, с которыми действуют друг на друга два взаимодействующих тела, всегда равны друг другу по величине и направлены в противоположные стороны
Силы F12 и F21 приложены к разным телам. Это значит, что эти силы не компенсируют друг друга. Третий закон справедлив для сил любой природы.
Любая система отсчёта, движущаяся равномерно и прямолинейно относительно инерциальной системы отсчёта является инерциальной 
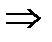
17. 
Ответ: Рассмотрим систему из нескольких взаимодействующих между собой тел. В результате взаимодействия между собой этих тел возникают силы F12, F13, F21, F23, F31, F32.
18. Какие силы, называют внутренними, а какие внешними? Приведите примеры.
Ответ:На тело 1 со стороны тела 2 действует сила F12, со стороны тела 3 – сила F13, на тело 2 со стороны тела 1 действует сила F21, со стороны тела 3 – сила F23 и т.д. Это внутренние силы, т.е. силы, возникающие в результате взаимодействия двух тел, принадлежащих рассматриваемой системе.
Пусть также каждое из тел взаимодействует с телом, не принадлежащем системе. В результате взаимодействия тела 1 с внешним телом возникает сила F1, в результате
взаимодействия тела 2 с внешним телом – сила F2 и т.д. Это – внешние силы, т.е. силы, возникающие в результате взаимодействия тела, принадлежащего системе с телом, не принадлежащим системе.
Примеры: рассмотрим движение Солнечной системы: притяжение Земли к Солнцу – внутренняя сила; если рассмотреть движение системы Земля – Луна, то для этой системы та же сила будет внешней.
19. Какие системы тел называют замкнутыми?
Ответ:Замкнутая система тел – совокупность физических тел, у которых взаимодействие с внешними телами отсутствуют.
20. Как приращение импульсаматериальной точки связано с импульсом силы? О какой силе при этом идёт речь?
21. Сформулируйте закон сохранения импульса для системы тел.
Ответ:Полный импульс системы тел постоянен во времени, если на систему не действуют внешние силы или сумма внешних сил равна нулю. Полный импульс – суммарный импульс всех тел, принадлежащих системе.
Импульс каждого из тел, принадлежащих системе, может изменяться. Однако изменение импульса одного тела обязательно будет скомпенсировано изменением импульса других тел.
22. Что такое работа силы? Что такое мощность? В каких единицах они измеряются?
Ответ:Чтобы количественно характеризовать процесс обмена энергией между взаимодействующими телами, в механике вводится понятие работа силы.
Если тело движется прямолинейно и на него действует постоянная сила F, которая составляет некоторый угол 

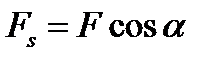


Единица работы – 1 джоуль (1 Дж= 1 H 
Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности.
Мощность–физическая величина, равная скорости изменения преобразования, передачи или потребления энергии системы. Мощность равна отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени: 

Единица мощности – 1 ватт (1 Вт = 1Дж/с).
23. Что такое кинетическая энергия материальной точки? С работой какой силы она связана и как?
Ответ:Пусть вдоль оси x движется частица массой m. Пусть на частицу действует постоянная сила F, параллельная оси x. Динамическое уравнение, спроецированное на ось x, будет иметь вид: 

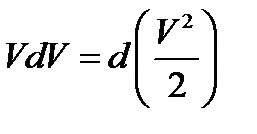




24. Какие силы называют консервативными? Приведите примеры таких сил.
Ответ:Работа силы по перемещению частицы из одной точки в другую в общем случае зависит от формы траектории между этими точками. Существуют силы, работа которых не зависит от формы траектории, а определяется только положением начальной и конечной точки. Такие силы называются консервативными. Определение: сила является консервативной, если её работа на замкнутой траектории равна нулю 
Примеры: сила тяжести, сила упругости – консервативные силы. Консервативными являются все силы, которые обратно пропорциональны квадрату расстояния между взаимодействующими телами.
25. Что такое потенциальная энергия материальной точки? С работой какой силы она связана и как?
Ответ:Потенциальная энергия – механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.В то время, как кинетическая энергия всегда характеризует тело относительно выбранной системы отсчёта, потенциальная энергия всегда характеризует тело относительно источника силы (силового поля).
Потенциальная энергия связана с силой тяжести. Рассмотрим тело, находящееся на высоте h над землёй. Если тело закреплено, то сила тяжести не совершает работу. Но сила тяжести потенциально способна совершить работу: если тело освободить, оно начнёт перемещаться и сила тяжести будет совершать работу.
26. Что такое полная механическая энергия материальной точки? С работой какой силы она связана и как?
Ответ:Пусть некоторая частица находится в стационарном поле консервативных сил. Со стороны этого поля на частицу действует консервативная сила Fконс. Работа, совершаемая этой силой, с одной стороны, идёт на приращение кинетической энергии частицы, движущейся под действием силы Fконс, а с другой – равна убыли потенциальной энергии этой частицы. Но это значит, что приращение кинетической энергии частицы равно убили её потенциальной энергии 


27. Сформулируйте закон сохранения механический энергии для материальной точи.
Ответ:Полная механическая энергия частицы может измениться под действием только сторонних сил. Отсюда вытекает закон сохранения механической энергии частицы: если сторонние силы отсутствуют или не совершают работы, то полная механическая энергия частицы в стационарном поле потенциальных сил остается постоянной.
28. Что такое полная механическая энергия системы материальных точек. С работой какой силы она связана и как?
Ответ:Пусть имеется система из двух взаимодействующих тел.Предположим, что силы, возникающие при взаимодействии этих тел, консервативны. Если под действием внутренних сил одно из тел изменит своё положение относительно другого, то работа внутренней силы будет равна убыли его потенциальной энергии. Потенциальная энергия этого тела обусловлена его взаимодействием с другим телом, принадлежащим этой системе. Поэтому её называют потенциальной энергией взаимодействия тел системы, или потенциальной энергией системы тел.
29. Сформулируйте закон сохранения механической энергии для системы материальных точек.
30. Какой вид взаимодействия тел называют абсолютно упругим ударом? Приведите примеры.
Ответ: Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.
Для математического описания простейших абсолютно упругих ударов используется закон сохранения энергии и закон сохранения импульса.
31. Какой вид взаимодействия тел называют абсолютно неупругим ударом? Приведите примеры.
32. Какие силы называют диссипативными? Приведите примеры.
Ответ:Диссипативныесилы — силы, при действии которых на механическую систему её полная механическая энергия убывает (то есть диссипирует), переходя в другие, немеханические формы энергии, например, в теплоту.
Пример: сила трения скольжения.
Ответы на вопросы для защиты лабораторных работ №2,3 по физике :3
1. Дайте определение понятия «вращательное движение».
Ответ:Вращательное движение – движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
2. Дайте определение угловой координаты.
Ответ:Угловая координата – полярный угол, на который можно повернуть против часовой стрелки полярную ось, для того чтобы попасть в точку, для которой определена данная угловая координата.
3. Дайте определение вектора углового перемещения. Как определяется его направление?
Ответ:Рассмотрим твёрдое тело, которое вращается вокруг неподвижной оси. Каждая точка этого тела описывает окружность равных промежутков. Бесконечно малые повороты 
Модуль вектора 
4. Дайте определение вектора угловой скорости. Как определяется его направление?
Ответ:Вектор угловой скорости – скользящий вектор, численно равный абсолютной величине угловой скорости и направленный вдоль оси вращения по правилу правого винта.

5. Дайте определение вектора углового ускорения. Как определяется его направление?
Ответ:Вектор углового ускорения – производная по времени от вектора угловой скорости тела.

6. Дайте определение момента инерции (как рассчитывается и каков его физический смысл?)
Момент инерции — величина аддитивная: момент инерции тела относительно некоторой оси равен сумме моментов инерции частей тела относительно той же оси.
Физический смысл: момент инерции является мерой инертности тела при вращении: 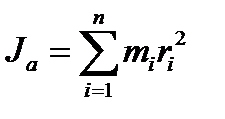
Осевой момент инертности тела Jaявляется мерой инертности тела во вращательном движении вокруг оси, подобно тому, как масса является мерой его инертности в поступательном движении. 
7. Дайте определение вектора момента импульса относительно точки, момента импульса относительно оси. Укажите направление вектора моментимпульса.
Ответ:Момент импульса относительно точки – векторная физическая величина, равная произведению радиус-вектора, проведённого от оси вращения к точке приложения импульса, на вектор этого импульса 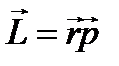
Момент импульса относительно неподвижной оси z– скалярная величина, равная проекции на эту ось вектора момента импульса, определённого относительно произвольной точки О данной оси.
8. Дайте определение вектора момента силы относительно точки, момента силы относительно оси. Укажите направление вектора момент силы.
Момент силы направлен перпендикулярно плоскости, образованной точкой О и вектором силы, в ту сторону от этой плоскости, из которой силы Fвидна ориентированной против движения часовой стрелки.
Момент силы относительно оси – момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью. 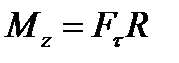


9. Назовите единицу измерения угловой скорости в системе СИ.
10. Назовите единицу измерения углового ускорения в системе СИ.
11. Назовите единицу измерения момента импульса в системе СИ.
12. Назовите единицу измерения момента силы в системе СИ.
13. Назовите единицу измерения момента инерции в системе СИ.
14. Как связаны линейные и угловые кинематические характеристики при вращательном движении?
Ответ:Связь угловой и линейной скоростями.За время dt все точки тела повернутся на угол 










Связь между угловой и линейной ускорениями. По определению 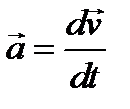




Линейные и угловые величины определяются аналогично. 
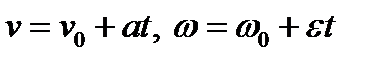
15. Как рассчитывается работа сил при вращательном движении?
Ответ:Поскольку взаимное расположение частиц твёрдого тела при вращении не изменяется, элементарная работа внешних сил над телом будет равна приращению кинетической энергии этого тела 



Работа на конечном угловом перемещении равна интегралу от элементарной работы, т.е. 
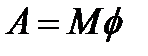
16. Как рассчитывается кинетическая энергия тела, вращающегося вокруг неподвижной оси?
Ответ:Представим тело, вращающееся относительно оси z, как совокупность элементарных масс. Скорость i-й элементарной массы, находящейся на расстоянии r, от оси вращения, 
Её кинетическая энергия 

17. Как связаны кинетическая энергия тела и работа сил при вращательном движении?
Ответ:Поскольку взаимное расположение частиц твёрдого тела при вращении не изменяется, элементарная работа внешних сил над телом будет равна приращению кинетической энергии этого тела 

18. Как связаны вектор момента импульса и вектор момента силы при вращательном движении тела?
Ответ:Возьмём производную по времени от выражения, определяющегомомент импульса:





Проекция последнего уравнения на ось z выражает связь момента импульса относительно оси z и момента силы относительно той же оси.
19. Сформулируйте теорему Штейнера.
Ответ:Теорема Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы тела на квадрат расстояния между осями 
20. Сформулируйте основной закон динамики вращательного движения.
Ответ:Момент силы, действующий на вращающееся тело, равен произведению момента инерции тела на угловое ускорение.
Момент импульса всего тела равен сумме моментов импульсов всех элементарных масс: 
Скорость v у разных элементарных масс различна, а угловая скорость одинакова. Поскольку 

Поскольку угловая скорость одинакова для всех элементарных масс, её можно вынести за знак суммы
Введём обозначение 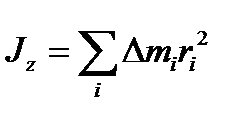
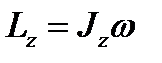
Момент импульса и момент силы связаны следующим образом 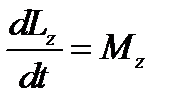
Заменив 
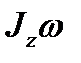


Учитывая, что производная угловой скорости по времени равна угловому ускорению 

21. Сформулируйте закон сохранения момента импульса для системы тел.
Ответ:Момент импульса системы материальных частиц будет постоянным во времени, если суммарный момент внешних сил равен нулю. Момент импульса системы будет сохраняться и в том случае, когда сумма внешних сил отлична от нуля, но суммарный момент внешних сил равен нулю.
Ответы на вопросы для защиты лабораторной работы №10 по физике :3
1. Назовите единицу измерения заряда в системе СИ.
2. Опишите основные свойства электрического заряда.
Ответ:Свойства электрического заряда:
1) электрический заряд существует в двух видах: как положительный, так и отрицательный;
2) в любой электрически изолированной системе алгебраическая сумма зарядов не изменяется;
3) электрический заряд является релятивистски инвариантным: его величина не зависит от системы отсчета, а значит, не зависит от того, движется он или покоится.
3. Сформулируйте основной закон сохранения электрического заряда.
Ответ:Основной закон сохранения электрического заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остаётся неизменной, какие бы процессы не происходили внутри этой системы.
4. Что такое электрическое поле? Назовите силовую и энергетическую характеристики электрического поля.
Ответ:Взаимодействие между зарядами осуществляется через поле. Всякий электрический заряд qизменяет определенным образом свойства окружающего его пространства – создаёт электрическое поле. Электрическое поле – вид материи, посредством которого осуществляется взаимодействие электрических зарядов.
5. 
Ответ:Однородное электрическое поле – электрическое поле, в котором напряженность одинакова по модулю и направлению в любой точке пространства.
Приблизительно однородным является электрическое поле между двумя разноименно заряженными плоскими металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу. (рис 133)
6. 
Ответ:Закон Кулона формулируется с помощью соотношения 

Пусть 


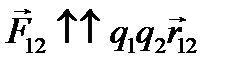
Умножение правой части 
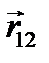


7. Сформулируйте принцип суперпозиции применительно к кулоновской силе.
Ответ:Принцип суперпозиции применительно к кулоновской силе:сила, действующая на заряд со стороны нескольких других зарядов, равна векторной сумме всех сил, действующих на интересующий нас заряд со стороны каждого из окружающих его зарядов в отдельности.
8. Дайте определение вектора напряженности электрического поля Е.
Ответ:Напряженность электрического поля в данной точке – векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силыF, действующей на неподвижный точечный заряд, помещенный в данную точку поля, к величине этого зарядаq.
9. Сформулируйте принцип суперпозиции для напряженности электрического поля E
Ответ:Принцип суперпозиции для напряженности электрического поля E:напряженность поля, созданного несколькими зарядами в интересующей нас точке, равна векторной сумме напряженностей, созданным каждым из зарядов в этой точке. 
10. Дайте определение характеристик зарядов, распределенных по нити, поверхности, объему.
Ответ:Величина dq (малая порция распределённого заряда (например, поле, созданное заряженной нитью)) может быть выражена следующим образом:
1) Если заряд распределён по линии, то 


2) Если заряд распределён по поверхности, то 


3) Если заряд распределён по объёму, то 

11. Дайте определение потока вектора напряженности.
Ответ:Пусть в некоторой области пространства существует электрическое поле. Выберем в этом поле элементарную площадку 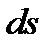
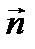

Потоком вектора напряженности электрического поля через эту площадку называется величина равная 


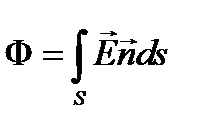
12. Сформулируйте теорему Гаусса для электрического поля в вакууме.
Ответ: Теорема Гаусса устанавливает связь между потоком вектора напряжённости через замкнутую поверхность с суммарным зарядом, охваченным этой поверхностью.
Теорема Гаусса: поток вектора напряженности электрического поля через замкнутую поверхность равен отношению суммы зарядов, охваченных этой поверхностью, к электрической постоянной. 

13. Напишите формулу для расчета напряженности электростатического поля бесконечной прямолинейной равномерно заряженной нити.
Ответ:Электростатическое поле – поле, порождённое неподвижными электрическими зарядами. 
14. Напишите формулу для расчета напряженности электростатического поля бесконечной равномерно заряженной плоскости.
Ответ:
15. Напишитеформулу для расчета напряженности электростатического поля внутри и вне равномерно заряженной сферы.
Ответ:Снаружи сферы: 


16. Дайте определение потенциала электростатического поля 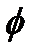
Ответ:Потенциал электростатического поля – скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещенный в данную точку поля. Единица измерения в СИ – вольт (1Дж/Кл). 


17. Сформулируйте принцип суперпозиции для потенциала электрического поля 
Ответ:Принцип суперпозиции для потенциала электрического поля 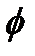
18. Чему равна работа электростатических сил по перемещению заряда? От чего она зависит?
Ответ:Если заряд движется в электростатическом поле, то кулоновская сила совершает работу. Допустим, что заряд 




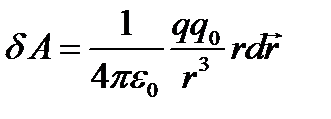


В конечном перемещении из точки 1 в точку 2 работа электростатических сил 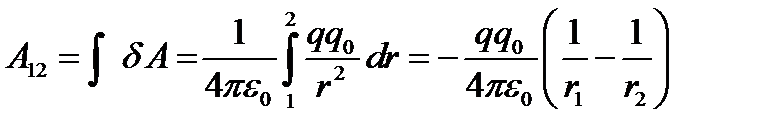
19. Как связаны напряженность и потенциал?
Ответ:В механике показано, что в консервативных полях выполняется соотношение 
Поскольку в электростатическом поле 

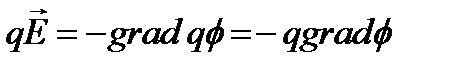

В декартовых координатах это выражение имеет вид: 
20. Что такое электрический диполь? Дайте определение дипольного момента.
Ответ:Электрический диполь – система из двух одинаковых по величине и противоположных по знаку зарядов, находящихся на расстоянии l друг от друга.
Основной характеристикой диполя является дипольный момент, который по определению равен 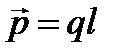

Дипольный момент есть векторная величина, прямо пропорциональная величине зарядов диполя и расстоянию между ними. Дипольный момент направлен так же, как и плечо диполя – от отрицательного заряда к положительному.
21. Чему равен момент пары сил, действующий на диполь в однородном электрическом поле?
Ответ:Если поместить диполь в однородное электрическое поле напряжённостью 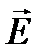

Векторная сумма этих сил равна нулю, поэтому диполь не будет двигаться поступательно. Но эти силы создают момент пары сил, который стремится повернуть диполь так, чтобы диполь был параллелен силовым линиям. Величина момента пары сил, действующего на диполь равна 
22. Что такое силовые линии и эквипотенциальные поверхности электрического поля? Под каким углом они пересекаются?
Ответ: Силовая линия – это линия, касательная к которой в каждой точке совпадает по направлению с вектором напряжённости поля в этой точке. Силовые линии начинаются на положительных зарядах и заканчиваются на отрицательных.
Эквипотенциальные поверхности – поверхности, все точки которых имеют одинаковый потенциал.
Угол пересечения равен 90 0 . Пояснение: Если какой-либо заряд перемещается по эквипотенциальной поверхности, то работа электростатических сил равна нулю