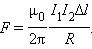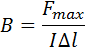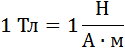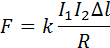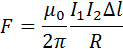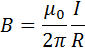Доказать что антипараллельные токи отталкиваются

6.5. Взаимодействие двух проводников с током

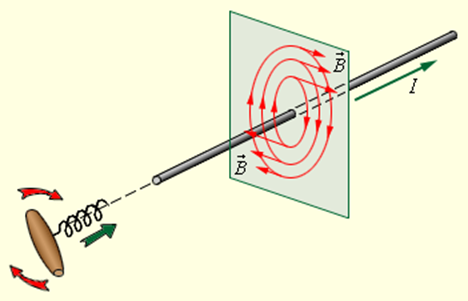
Применим закон Ампера для вычисления силы взаимодействия двух длинных прямолинейных проводников с токами I₁ и I₂, находящихся на расстоянии d друг от друга (рис. 6.26).

Рис. 6.26. Силовое взаимодействие прямолинейных токов:
1 — параллельные токи; 2 — антипараллельные токи

Проводник с током I₁ создает кольцевое магнитное поле, величина которого в месте нахождения второго проводника равна

Это поле направлено «от нас» ортогонально плоскости рисунка. Элемент второго проводника испытывает со стороны этого поля действие силы Ампера

Подставляя (6.23) в (6.24), получим

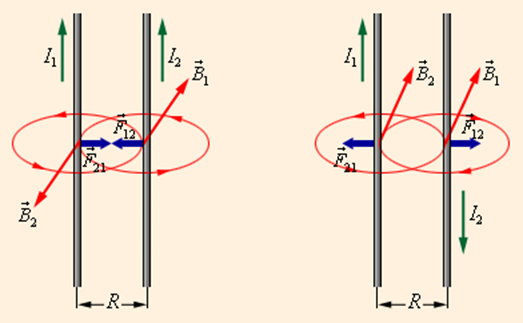
При параллельных токах сила F₂₁ направлена к первому проводнику (притяжение), при антипараллельных — в обратную сторону (отталкивание).

Аналогично на элемент проводника 1 действует магнитное поле, создаваемое проводником с током I₂ в точке пространства с элементом с силой F₁₂. Рассуждая таким же образом, находим, что F₁₂ = –F₂₁, то есть в этом случае выполняется третий закон Ньютона.

Итак, сила взаимодействия двух прямолинейных бесконечно длинных параллельных проводников, рассчитанная на элемент длины проводника, пропорциональна произведению сил токов I₁ и I₂ протекающих в этих проводниках, и обратно пропорциональна расстоянию между ними. В электростатике по аналогичному закону взаимодействуют две длинные заряженные нити.

На рис. 6.27 представлен опыт, демонстрирующий притяжение параллельных токов и отталкивание антипараллельных. Для этого используются две алюминиевые ленты, подвешенные вертикально рядом друг с другом в слабо натянутом состоянии. При пропускании через них параллельных постоянных токов силой около 10 А ленты притягиваются. а при изменении направления одного из токов на противоположное — отталкиваются.

Рис. 6.27. Силовое взаимодействие длинных прямолинейных проводников с током

На основании формулы (6.25) устанавливается единица силы тока — ампер, являющаяся одной из основных единиц в СИ.

Ампер — это сила неизменяюшегося тока, который, протекая по двум длинным параллельным проводникам, расположенным в вакууме на расстоянии 1 м, вызывает между ними силу взаимодействия 2×10 –7 Н на каждый метр длины провода.

Пример. По двум тонким проводам, изогнутым в виде одинаковых колец радиусом R = 10 см, текут одинаковые токи I = 10 А в каждом. Плоскости колец параллельны, а центры лежат на ортогональной к ним прямой. Расстояние между центрами равно d = 1 мм. Найти силы взаимодействия колец.

Решение. В этой задаче не должно смущать, что мы знаем лишь закон взаимодействия длинных прямолинейных проводников. Поскольку расстояние между кольцами много меньше их радиуса, взаимодействующие элементы колец «не замечают» их кривизны. Поэтому сила взаимодействия дается выражением (6.25), куда вместо надо подставить длину окружности колец Получаем тогда

Источник

Доказать что антипараллельные токи отталкиваются

Первыми экспериментами (проведены в 1820 г.), показавшими, что между электрическими и магнитными явлениями имеется глубокая связь, были опыты датского физика Х. Эрстеда. Эти опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся ее повернуть. В том же году французский физик А. Ампер наблюдал силовое взаимодействие двух проводников с токами и установил закон взаимодействия токов.

По современным представлениям, проводники с током оказывают силовое действие друг на друга не непосредственно, а через окружающие их магнитные поля.

Источниками магнитного поля являются движущиеся электрические заряды (токи). Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).

Ученые XIX века пытались создать теорию магнитного поля по аналогии с электростатикой, вводя в рассмотрение так называемые магнитные заряды двух знаков (например, северный и южный полюса магнитной стрелки). Однако опыт показывает, что изолированных магнитных зарядов не существует.

Магнитное поле токов принципиально отличается от электрического поля. Магнитное поле, в отличие от электрического, оказывает силовое действие только на движущиеся заряды (токи).

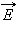
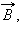
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности электрического поля. Такой характеристикой является вектор магнитной индукции который определяет силы, действующие на токи или движущиеся заряды в магнитном поле.

Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока в проводнике и его длине Δ:

В общем случае сила Ампера выражается соотношением:

В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (Тл).

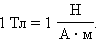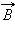
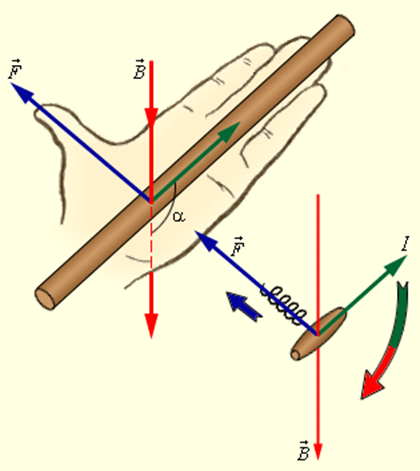
Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки : если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (рис. 1.16.2).

Одним из важных примеров магнитного взаимодействия является взаимодействие параллельных токов. Закономерности этого явления были экспериментально установлены Ампером. Если по двум параллельным проводникам электрические токи текут в одну и ту же сторону, то наблюдается взаимное притяжение проводников. В случае, когда токи текут в противоположных направлениях, проводники отталкиваются.

Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот.

Опыты показали, что модуль силы, действующей на отрезок длиной Δ каждого из проводников, прямо пропорционален силам тока ₁ и ₂ в проводниках, длине отрезка Δ и обратно пропорционален расстоянию между ними:

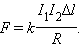В Международной системе единиц СИ коэффициент пропорциональности принято записывать в виде:

Формула, выражающая закон магнитного взаимодействия параллельных токов, принимает вид:

Для того, чтобы при магнитном взаимодействии параллельные токи притягивались, а антипараллельные отталкивались, линии магнитной индукции поля прямолинейного проводника должны быть направлены по часовой стрелке, если смотреть вдоль проводника по направлению тока. Для определения направления вектора 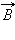магнитного поля прямолинейного проводника также можно пользоваться правилом буравчика: направление вращения рукоятки буравчика совпадает с направлением вектора если при вращении буравчик перемещается в направлении тока (рис. 1.16.3).

Рис. 1.16.4 поясняет закон взаимодействия параллельных токов.

Магнитное взаимодействие параллельных проводников с током используется в Международной системе единиц (СИ) для определения единицы силы тока – ампера:

Ампер – сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, равную на каждый метр длины.

Источник

Магнитное взаимодействие токов

Магнитные явления были известны еще в древнем мире. Компас был изобретен более 4500 лет тому назад. В Европе он появился приблизительно в XII веке новой эры. Однако только в XIX веке была обнаружена связь между электричеством и магнетизмом и возникло представление о магнитном поле.

Первыми экспериментами (проведены в 1820 г.), показавшими, что между электрическими и магнитными явлениями имеется глубокая связь, были опыты датского физика Ханса Эрстеда. Эти опыты показали, что на магнитную стрелку, расположенную вблизи проводника с током, действуют силы, которые стремятся ее повернуть. В том же году французский физик Андре Ампер наблюдал силовое взаимодействие двух проводников с токами и установил закон взаимодействия токов.

По современным представлениям, проводники с током оказывают силовое действие друг на друга не непосредственно, а через окружающие их магнитные поля.

Источниками магнитного поля являются движущиеся электрические заряды. Магнитное поле возникает в пространстве, окружающем проводники с током, подобно тому, как в пространстве, окружающем неподвижные электрические заряды, возникает электрическое поле. Магнитное поле постоянных магнитов также создается электрическими микротоками, циркулирующими внутри молекул вещества (гипотеза Ампера).

Ученые XIX века пытались создать теорию магнитного поля по аналогии с электростатикой, вводя в рассмотрение так называемые магнитные заряды двух знаков (например, северный N и южный S полюса магнитной стрелки). Однако опыт показывает, что изолированных магнитных зарядов не существует.

Магнитное поле токов принципиально отличается от электрического поля. Магнитное поле, в отличие от электрического, оказывает силовое действие только на движущиеся заряды (токи).

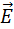
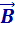
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности электрического поля. Такой характеристикой является вектор магнитной индукции который определяет силы, действующие на токи или движущиеся заряды в магнитном поле.

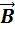
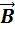
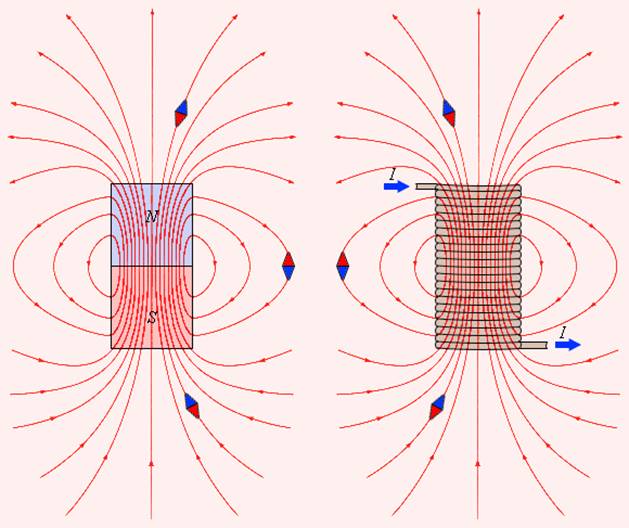
За положительное направление вектора принимается направление от южного полюса S к северному полюсу N магнитной стрелки, свободно ориентирующийся в магнитном поле. Таким образом, исследуя магнитное поле, создаваемое током или постоянным магнитом, с помощью маленькой магнитной стрелки, можно в каждой точке пространства определить направление вектора . Такое исследование позволяет наглядно представить пространственную структуру магнитного поля. Аналогично силовым линиям в электростатике можно построить линии магнитной индукции, в каждой точке которых вектор направлен по касательной. Пример линий магнитной индукции полей постоянного магнита и катушки с током приведен на рис. 1.16.1.

Линии магнитной индукции полей постоянного магнита и катушки с током. Индикаторные магнитные стрелки ориентируются по направлению касательных к линиям индукции

Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.

Для того, чтобы количественно описать магнитное поле, нужно указать способ определения не только направления вектора 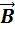но и его модуля. Проще всего это сделать, внося в исследуемое магнитное поле проводник с током и измеряя силу, действующую на отдельный прямолинейный участок этого проводника. Этот участок проводника должен иметь длину Δl, достаточно малую по сравнению с размерами областей неоднородности магнитного поля. Как показали опыты Ампера, сила, действующая на участок проводника, пропорциональна силе тока I, длине Δl этого участка и синусу угла α между направлениями тока и вектора магнитной индукции:

Эта сила называется силой Ампера. Она достигает максимального по модулю значения F_max, когда проводник с током ориентирован перпендикулярно линиям магнитной индукции. Модуль вектора 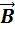определяется следующим образом:

Модуль вектора магнитной индукции равен отношению максимального значения силы Ампера, действующей на прямой проводник с током, к силе тока I в проводнике и его длине Δl:

В общем случае сила Ампера выражается соотношением:

Это соотношение принято называть законом Ампера.

В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется Тесла (Тл).

Тесла – очень крупная единица. Магнитное поле Земли приблизительно равно 0,5·10 –4 Тл. Большой лабораторный электромагнит может создать поле не более 5 Тл.

Сила Ампера направлена перпендикулярно вектору магнитной индукции 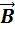и направлению тока, текущего по проводнику. Для определения направления силы Ампера обычно используют правило левой руки: если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы, действующей на проводник (рис. 1.16.2).

Правило левой руки и правило буравчика

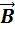
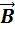
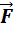
Если угол α между направлениями вектора и тока в проводнике отличен от 90°, то для определения направления силы Ампера более удобно пользоваться правилом буравчика: воображаемый буравчик располагается перпендикулярно плоскости, содержащей вектор и проводник с током, затем его рукоятка поворачивается от направления тока к направлению вектора Поступательное перемещение буравчика будет показывать направление силы Ампера (рис. 1.16.2). Правило буравчика часто называют правилом правого винта.

Одним из важных примеров магнитного взаимодействия является взаимодействие параллельных токов. Закономерности этого явления были экспериментально установлены Ампером. Если по двум параллельным проводникам электрические токи текут в одну и ту же сторону, то наблюдается взаимное притяжение проводников. В случае, когда токи текут в противоположных направлениях, проводники отталкиваются.

Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот.

Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I₁ и I₂ в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:

В Международной системе единиц СИ коэффициент пропорциональности k принято записывать в виде:

где μ₀ – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно

Формула, выражающая закон магнитного взаимодействия параллельных токов, принимает вид:

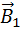
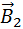
Отсюда нетрудно получить выражение для индукции магнитного поля каждого из прямолинейных проводников. Магнитное поле прямолинейного проводника с током должно обладать осевой симметрией и, следовательно, замкнутые линии магнитной индукции могут быть только концентрическими окружностями, располагающимися в плоскостях, перпендикулярных проводнику. Это означает, что векторы и магнитной индукции параллельных токов I₁ и I₂ лежат в плоскости, перпендикулярной обоим токам. Поэтому при вычислении сил Ампера, действующих на проводники с током, в законе Ампера нужно положить sin α = 1. Из закона магнитного взаимодействия параллельных токов следует, что модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением

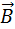
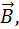
Для того, чтобы при магнитном взаимодействии параллельные токи притягивались, а антипараллельные отталкивались, линии магнитной индукции поля прямолинейного проводника должны быть направлены по часовой стрелке, если смотреть вдоль проводника по направлению тока. Для определения направления вектора магнитного поля прямолинейного проводника также можно пользоваться правилом буравчика: направление вращения рукоятки буравчика совпадает с направлением вектора если при вращении буравчик перемещается в направлении тока (рис. 1.16.3).

Магнитное поле прямолинейного проводника с током

Магнитное взаимодействие параллельных и антипараллельных токов

Рис. 1.16.4 поясняет закон взаимодействия параллельных токов.

Магнитное взаимодействие параллельных проводников с током используется в Международной системе единиц (СИ) для определения единицы силы тока – ампера:

Ампер – сила неизменяющегося тока, который при прохождении по двум параллельным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м один от другого в вакууме, вызвал бы между этими проводниками силу магнитного взаимодействия, равную 2·10 –7 Н на каждый метр длины.

Источник

Учебники

Журнал «Квант»

Общие

Рыбин Б. Почему висит кольцо //Квант. — 1992. — № 9. — С. 47-49.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

Поговорим о двух опытах, которые вы можете провести в школьном физическом кабинете.

Первый опыт

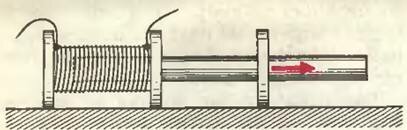
Возьмите длинный железный стержень круглого сечения и вставьте его одним концом в катушку, длина которой в несколько раз меньше длины стержня. Расположите сердечник с катушкой горизонтально (см. рисунок). На выступающий конец сердечника наденьте легкое алюминиевое кольцо, диаметр которого чуть больше диаметра сердечника. К катушке через ключ подсоедините источник постоянного тока, напряжение на выходе которого можно при желании изменять.

Придвиньте алюминиевое кольцо вплотную к катушке и замкните ключ — кольцо оттолкнется от катушки. Величину постоянного тока можно подобрать так, чтобы кольцо удалилось почти на всю длину сердечника. Теперь разомкните цепь — кольцо возвратится почти в исходное положение.

Объяснение этого опыта кажется не очень сложным. Приведем его. Площадь, ограниченную алюминиевым кольцом, пронизывает магнитный поток, создаваемый током в катушке. При замыкании ключа этот магнитный поток растет, и по правилу Ленца в кольце возникает индукционный ток, направленный противоположно току в катушке. Антипараллельные токи отталкиваются, следовательно, кольцо действительно должно отталкиваться от катушки. При размыкании цепи магнитный поток уменьшается, и в кольце возникает ток, сонаправленный току в катушке. Такие токи притягиваются друг к другу, вот почему кольцо приближается к катушке.

Второй опыт

Расположите сердечник вертикально так, чтобы катушка находилась в нижней его части, и наденьте на него алюминиевое кольцо. Подключите к катушке источник переменного синусоидального тока (можно просто включить катушку в сеть, а для регулирования величины напряжения последовательно катушке подсоединить реостат) и замкните цепь. Кольцо, лежащее на катушке, приподнимается и висит в воздухе все время, пока по катушке идет ток. Если амплитуда тока достаточно большая, то в момент включения кольцо может даже слететь с сердечника.

Как же можно объяснить этот опыт? Попробуем сначала провести такие же рассуждения, как и в первом случае.

В течение той четверти периода, когда величина тока в катушке растет, в кольце возникает индукционный ток, направленный противоположно току в катушке, и между кольцом и катушкой возникают силы отталкивания. В течение следующей четверти периода, когда величина тока в катушке уменьшается, между кольцом и катушкой действуют силы притяжения. Таким образом, на кольцо должна действовать быстро меняющаяся по направлению сила. Среднее значение этой силы равно нулю, поэтому кольцо, казалось бы, не должно приподниматься и тем более висеть в воздухе.

В чем же дело?

Причина возникшего противоречия между приведенным объяснением и реальным поведением кольца заключена в следующем. Магнитный поток, пронизывающий площадку, ограниченную кольцом, создается не только током, идущим по катушке, но и индукционным током, возникающим в самом кольце (явление самоиндукции). И если при объяснении первого опыта пренебрежение этим фактором не привело к ошибочным выводам, то во втором случае мы пришли к противоречию. Попробуем разобраться, но прежде сформулируем три утверждения, которые нам понадобятся в дальнейшем.

Теперь мы можем дать объяснение второму опыту. Перед включением переменного тока магнитный поток Ф был равен нулю. Согласно третьему утверждению, он будет равен нулю и после включения тока. Отсюда следует, что все время, пока по катушке идет переменный ток, Ф₁ и Ф₂ равны по величине, но противоположны по знаку. Тогда из второго утверждения получаем, что токи в этом случае антипараллельны, а значит, на кольцо в течение всего опыта действует сила отталкивания. Если амплитуда тока достаточно велика, возникающая сила отталкивания будет больше силы тяжести кольца. Однако при удалении от катушки сила отталкивания становится меньше, и на некоторой высоте она оказывается равной силе тяжести — это и есть положение равновесия кольца. Если кольцо успело развить достаточно большую скорость, оно может проскочить положение равновесия и слететь с сердечника.

Вернемся к первому опыту и объясним его с тех же позиций, что и второй. Поведение кольца при включении постоянного тока ничем не отличается от его поведения при протекании переменного тока. Поэтому рассмотрим подробно только процесс выключения тока. За время между включением тока и его выключением индукционный ток, текущий в кольце, успевает обратиться в нуль (за счет джоулевых потерь). Поэтому перед выключением тока Ф = Ф₁. При выключении тока в катушке вместе с током I₁ начинает быстро уменьшаться и поток Ф₁. Одновременно в кольце возникает индукционный ток I₂, а с ним и магнитный поток Ф₂. Так как суммарный поток остается постоянным, знаки у Ф₁ и Ф₂ одинаковы. Это значит, что токи I₁ и I₂ — параллельны, следовательно, кольцо притягивается к катушке.

В заключение обсудим, что изменилось бы, если бы мы заменили алюминиевое кольцо на кольцо из сверхпроводника, сопротивление которого, как известно, не просто мало, а равно нулю. При включении тока это кольцо будет отталкиваться так же, как и алюминиевое. Однако теперь все время между включением тока и его выключением индукционный ток в кольце остается постоянным (R = 0, и джоулевы потери отсутствуют). Т. е. все время, пока по катушке идет ток, между катушкой и кольцом действуют силы отталкивания. Суммарный магнитный поток при этом остается равным нулю. При отключении источника тока I₁ и I₂ начинают убывать, оставаясь антипараллельными. Поэтому между кольцом и катушкой продолжают действовать силы отталкивания, правда, убывающие со временем.

Примечания

\tau \sim \frac LR\) (L — индуктивность кольца) должно быть гораздо больше периода изменения внешнего магнитного поля Т. Поскольку \(

T = \frac<2 \pi><\omega>\), условие малости R принимает вид \(

Источник