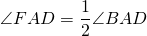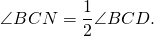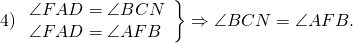Доказать что биссектрисы соседних углов параллелограмма перпендикулярны а противолежащих параллельны
Биссектрисы параллелограмма
Если биссектрисы углов параллелограмма, прилежащих к одной стороне перпендикулярны, то биссектрисы противолежащих углов обладают другим свойством.
Свойство биссектрис противоположных углов параллелограмма.
Биссектрисы противоположных углов параллелограмма параллельны или лежат на одной прямой.
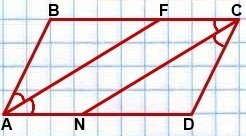
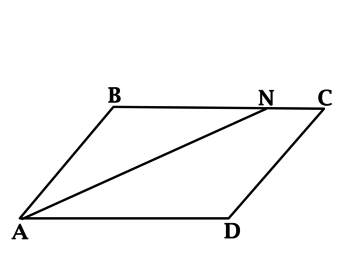
Дано: ABCD — параллелограмм,
AF — биссектриса ∠BAD,
CN- биссектриса ∠BCD.
Доказать: AF ∥ CN или лежат на одной прямой.
1) Так как AF — биссектриса ∠BAD, CN — биссектриса ∠BCD (по условию), то
Следовательно, их половины тоже равны: ∠FAD=∠BCN.
при BC ∥ AD и секущей BC).
А так как эти углы — соответственные при прямых AF и CN и секущей BC, то AF ∥ CN (по признаку параллельности прямых).
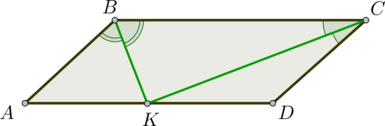
Если все стороны параллелограмма равны, биссектрисы противоположных углов лежат на одной прямой.
В этом случае из того, что AB=BC следует, что треугольник ABC — равнобедренный с основанием AC,
а значит, ∠BAC=∠BCA (как углы при основании равнобедренного треугольника).
А) Сумма односторонних углов, образованных параллельными прямыми и секущей, равна 180°.
Следовательно, сумма их половин∠АВО + ∠ВАО = (0, 5∠АВС + 0, 5∠ВАД) = 180° : 2 = 90°.
Б) Противоположные углы параллелограмма равны.
Равны и половины этих углов.
Аналогично доказывается параллельность или равенство биссектрис другой пары углов.
Пожалуйста, помогите доказать признак параллелограмма : биссектрисы соседних углов параллелограмма перпендикулярны?
Пожалуйста, помогите доказать признак параллелограмма : биссектрисы соседних углов параллелограмма перпендикулярны.
Докажите что если биссектрисы углов АОВ и ВОС перпендикулярны то точки А О и С лежат на одной прямой?
Докажите что если биссектрисы углов АОВ и ВОС перпендикулярны то точки А О и С лежат на одной прямой.
Докажите, что если биссектрисы углов АВС и СВD перпендикулярны, то точки А, В, D лежат на одной прямой?
Докажите, что если биссектрисы углов АВС и СВD перпендикулярны, то точки А, В, D лежат на одной прямой.
Докажите, что биссектрисы соседних углов параллелограмма пересекаются под прямым углом?
Докажите, что биссектрисы соседних углов параллелограмма пересекаются под прямым углом.
Докажите, что биссектрисы противоположных углов прямоугольника образуют параллелограмм?
Докажите, что биссектрисы противоположных углов прямоугольника образуют параллелограмм.
Доказательство о том, что биссектрисы соседних углов параллелограмма перпендикулярны?
Доказательство о том, что биссектрисы соседних углов параллелограмма перпендикулярны.
Докажите, что биссектрисы двух соседних углов параллелограмм перпендикулярны?
Докажите, что биссектрисы двух соседних углов параллелограмм перпендикулярны.
В параллелограмме проведены биссектрисы противоположных углов?
В параллелограмме проведены биссектрисы противоположных углов.
Докажите, что отрезки биссектрис, заключенные внутри параллелограмма равны.
Докажите, что биссектрисы вертикальных углов лежат на одной прямой?
Докажите, что биссектрисы вертикальных углов лежат на одной прямой.
Докажите, что биссектрисы вертикальных углов лежат на одной прямой?
Докажите, что биссектрисы вертикальных углов лежат на одной прямой.
Плюсы карты в том што она занимает мало места, легкая. Минусы размеры севера увеличиваются. Например на карте Островский Гренландия кажется больше чем материк Австралия.
Если в трапецию можно вписать окружность, то сумма боковых сторон равна сумме оснований. Средняя линия трапеции равна полусумме оснований. Зн. 21 / 2 = 10, 5(Средняя линия трапеции).
Параллелограмм: свойства и признаки
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
Биссектриса параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
Как найти площадь параллелограмма:
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
Если мы проведем обе диагонали в параллелограмме, точка пересечения разделит их пополам. Убедимся, так ли это:
Теорема доказана. Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
Шаг 3. Из равенства треугольников также следует:
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
Шаг 2. Из равенства треугольников следует, что CD = AB.
Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Параллелограмм: свойство его биссектрисы
Биссектриса параллелограмма — это отрезок, соединяющий вершину параллелограмма с точкой на одной из двух противоположных сторон и делящий угол при вершине пополам.
\(\bullet\) Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
Выпускники, которые рассчитывают успешно сдать ЕГЭ, в обязательном порядке должны повторить тему «Свойства биссектрисы параллелограмма». Как показывает статистика, при прохождении аттестационного испытания задачи по данному разделу планиметрии вызывают сложности у большого количества учащихся. При этом задания, в которых необходимо применить свойства биссектрисы угла параллелограмма, встречаются в ЕГЭ ежегодно. Таким образом, справляться с ними должны все учащиеся.
Образовательный портал «Школково» предлагает выстроить процесс подготовки к прохождению аттестационного испытания по-новому. Занимаясь вместе с нашим ресурсом, выпускники смогут определить наиболее сложные для себя темы и ликвидировать пробелы в знаниях.
Чтобы задания ЕГЭ не вызывали трудностей, рекомендуем вначале повторить основные понятия и свойства биссектрисы параллелограмма. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».
Для того чтобы окончательно понять принцип решения задач по данному разделу планиметрии, мы рекомендуем выполнить соответствующие упражнения. Большая подборка заданий различного уровня сложности представлена в разделе «Каталог». Для каждого упражнения на сайте приведен алгоритм решения и дан правильный ответ. Последовательно выполняя их, учащиеся смогут понять, как правильно применять свойства биссектрисы внутреннего угла параллелограмма.
Получать новые знания и оттачивать собственные навыки по данной теме или, например, в решении задач на тему «Прямоугольник» в ЕГЭ учащиеся могут в онлайн-режиме, находясь в Москве или любом другом российском городе. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.
Доказать что биссектрисы соседних углов параллелограмма перпендикулярны а противолежащих параллельны
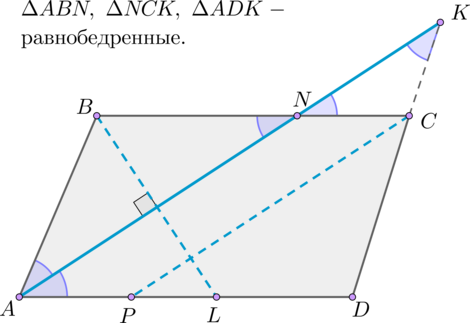
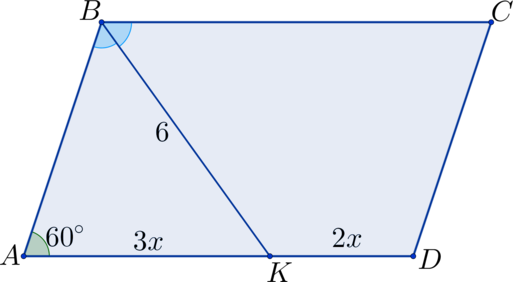
Решите задачу по данным рисунка.
Отрезки D1B и DB1 параллельны, поскольку лежат на параллельных сторонах параллелограмма. Биссектрисы DD1 и B1B противоположных углов параллелограмма также параллельны, поскольку углы AD1D и D1DC равны как накрест лежащие, при пересечении параллельных прямых АВ с CD секущей DD1, а тогда углы AD1D и D1BB1 — равные соответственные углы при пересечении прямых DD1 и B1B секущей АВ. Тем самым, четырехугольник BB1DD1 — параллелограмм, так как его противоположные стороны попарно параллельны. Тем самым,
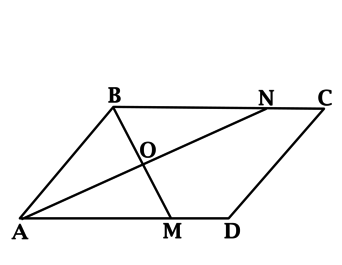
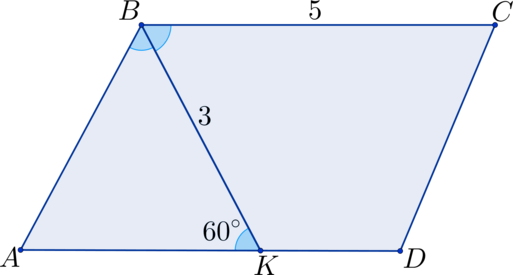
Решите задачу по данным рисунка.
Заметим, что — параллелограмм (
параллельны, поскольку лежат на противоположных сторонах параллелограмма;
параллельны, по свойству о биссектрисах противоположных углов параллелограмма). Диагональ
делит параллелограмм
на два равновеликих треугольника, поэтому его площадь равна двум площадям треугольника
то есть 22.