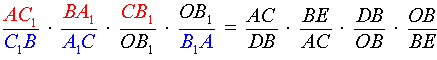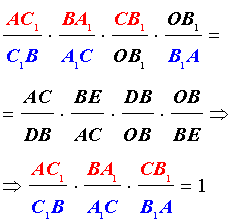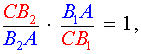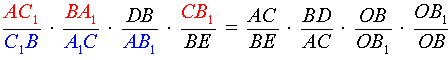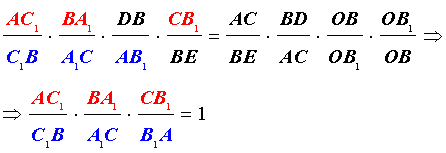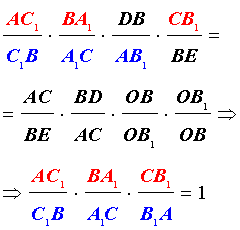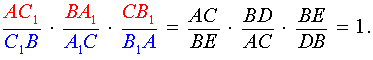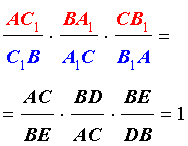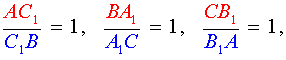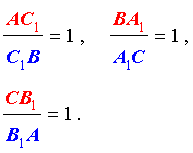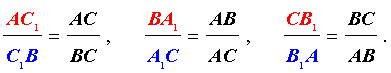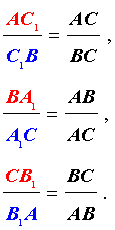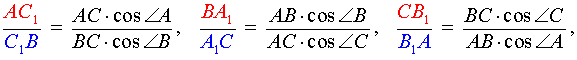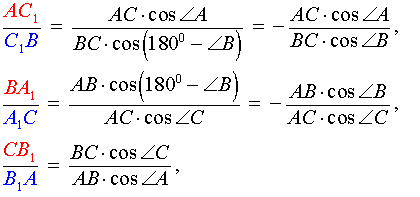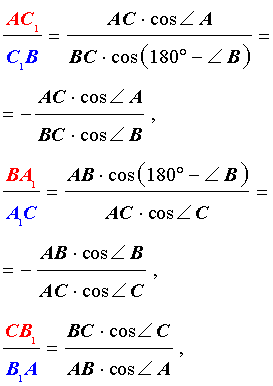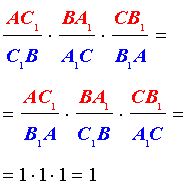Доказать что биссектрисы треугольника пересекаются в одной точке через теорему чевы

Теорема Чевы: формулировка и пример с решением

В данной публикации мы рассмотрим одну из классических теорем аффинной геометрии – теорему Чевы, которая получила такое название в честь итальянского инженера Джованни Чевы. Также разберем пример решения задачи, чтобы закрепить представленный материал.

Формулировка теоремы

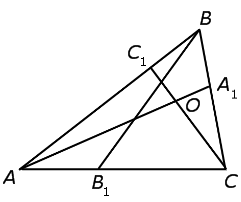
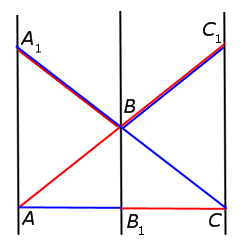
Дан треугольник ABC, в котором каждая вершина соединена с точкой на противоположной стороне.

Таким образом, мы получаем три отрезка (AA’, BB’ и CC’), которые называются чевианами.

Данные отрезки пересекаются в одной точке тогда и только тогда, когда выполняется следующее равенство:

Теорему можно, также, представить в таком виде (определяется, в каком соотношении точки делят стороны):

Тригонометрическая теорема Чевы

Примечание: все углы – ориентированные.

Пример задачи

Дан треугольник ABC с точками A’, B’ и C’ на сторонах BC, AC и AB, соответственно. Вершины треугольника соединены с данным точками, и образованные отрезки проходят через одну точку. При этом точки A’ и B’ взяты на серединах соответствующих противоположных сторон. Выясните, в каком соотношении точка C’ делит сторону AB.

Решение
Нарисуем чертеж согласно условиям задачи. Для нашего удобства примем следующие обозначения:

Остается только составить соотношение отрезков согласно теореме Чевы и подставить в него принятые обозначения:

После сокращения дробей получаем:

Значит, AC’ = C’B, т.е. точка C’ делит сторону AB пополам.

Следовательно, в нашем треугольнике отрезки AA’, BB’ и CC’ являются медианами. Решив задачу мы доказали, что они пересекаются в одной точке (справедливо для любого треугольника).

Примечание: с помощью теоремы Чевы можно доказать, что в треугольнике в одной точке, также, пересекаются биссектрисы или высоты.

Источник

Теорема Чевы

Теорема Чевы 1

.

(1)

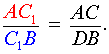(2)

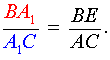(3)

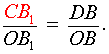(4)

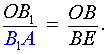(5)

Перемножая равенства (2 – 5), получим

Доказательство необходимости завершено.

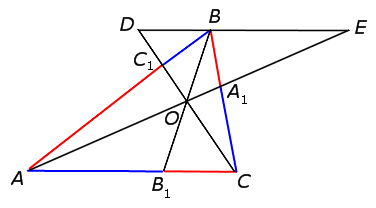
Воспользуемся методом «от противного». С этой целью обозначим буквой O точку пересечения отрезков AA₁ и CC₁ и предположим, что отрезок BB₁ не проходит через точку O (рис. 3).

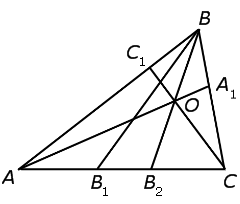
Проведём через точку O отрезок BB₂ (рис. 4).

Поскольку отрезки AA₁, BB₂ и CC₁ пересекаются в одной точке, то выполнено равенство

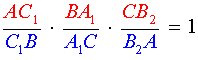(6)

Кроме того, выполнено равенство

(1)

Разделив равенство (6) на равенство (1), получим равенство

следствием которого является равенство

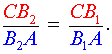(7)

Из равенства (7) вытекает, что точки B₁ и B₂ совпадают.

Доказательство достаточности завершено.

Теорема Чевы 2

.

(8)

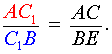(9)

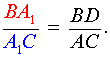(10)

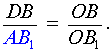(11)

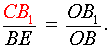(12)

Перемножая равенства (9 – 12), получим

Доказательство необходимости в случае «а» завершено.

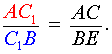(13)

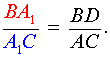(14)

Поскольку четырёхугольники ADBB₁ и BECB₁ параллелограммы, то выполнено равенство

откуда вытекает равенство

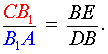(15)

Перемножая равенства (13 – 15), получим

Доказательство необходимости в случае «b» завершено.

Применения теоремы Чевы

В разделе нашего справочника «Медиана треугольника» доказана теорема о том, что медианы треугольника пересекаются в одной точке. Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим медианы AA₁, BB₁ и CC₁ треугольника ABC (рис.9).

то выполнено равенство

,

откуда вытекает, что отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке. Теорема доказана.

В разделе нашего справочника «Окружность, вписанная в треугольник» доказана теорема о том, что биссектрисы треугольника пересекаются в одной точке. Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим биссектрисы AA₁, BB₁ и CC₁ треугольника ABC (рис.10).

В соответствии со свойством биссектрисы справедливы равенства

Если перемножить эти три равенства, то мы получим равенство

,

из которого вытекает, что отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке. Теорема доказана.

В разделе нашего справочника «Высота треугольника» доказана теорема о том, что высоты треугольника пересекаются в одной точке. Приведём другое доказательство этой теоремы, основанное на теореме Чевы. С этой целью рассмотрим сначала высоты AA₁, BB₁ и CC₁ остроугольного треугольника ABC (рис.11).

то, перемножив эти три равенства, мы получим равенство

,

из которого вытекает, что отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке. Теорема о пересечении высот остроугольного треугольника доказана.

Теперь рассмотрим случай тупоугольного треугольника (рис. 12).

то, перемножив эти три равенства, мы получим равенство

,

из которого вытекает, что прямые AA₁, BB₁ и CC₁ пересекаются в одной точке. Теорема о пересечении высот тупоугольного треугольника доказана.

Доказывать теорему о том, что в случае прямоугольного треугольника все высоты пересекаются в одной точке не нужно, поскольку все высоты прямоугольного треугольника пересекаются в вершине прямого угла.

Теорема о пересечении высот треугольника доказана полностью.

Теперь с помощью теоремы Чевы докажем следующую теорему.

Из этих равенств получаем:

Отсюда с помощью теоремы Чевы заключаем, что отрезки AA₁, BB₁ и CC₁ пересекаются в одной точке. Теорема доказана.

Источник

Геометрия

понедельник, 14 сентября 2009 г.

Теорема Чевы. Простое доказательство и широкая применимость.

Помню, в школе мы доказывали, что медианы треугольника пересекаются в одной точке. И что биссектрисы треугольника пересекаются в одной точке. Более того, высоты и серединные перпендикуляры треугольника тоже обладают тем же свойством.
Вот только доказывались эти теоремы. как? Да в том-то и дело, что каждая из них доказывалась как-то по-своему, у каждой из них был свой способ.

Я хочу показать вам, дорогие читатели, единый способ доказательства этих теорем. Доказательства, использующего теорему Чевы.
Вот её формулировка:

Пусть точки A’,B’,C’ лежат на прямых BC,CA,AB треугольника . Прямые AA’,BB’,CC’ пересекаются в одной точке тогда и только тогда, когда

Прежде чем перейти к доказательству, замечу, что равенство в формулировке не такое уж заумное и трудно запоминающееся, как может показаться на первый взгляд. Действительно, чтобы получить это равенство, нам достаточно выбрать произвольную вершину треугольника, например, B, и начать обходить треугольник по часовой стрелке. Обойдя треугольник, мы пройдём по каждому из отрезков как раз в той последовательности, в которой они встречаются в равенстве.

С одной стороны,
S AOB’ /S COB’ =AB’/B’C
С другой стороны, это же отношение площадей равно отношению высот треугольников AOB’ и COB’, проведенных к основанию OB’, равно как и отношение площадей треугольников AOB и COB.

Таким образом, AB’/B’C = S AOB /S COB.

Записав аналогичные равенства для отношений CA’/A’B и AC’/C’B и затем перемножив их всех, получим требуемое утверждение.

Можно записать условие Чевы в форме синусов :
Это условие легко получить, применив теорему синусов к треугольникам ABA’ и ACA’. Для них получаем A’B/AA’= sinBAA’ /sinABA’ и A’C/AA’=sinA’AC/sinA’CA. Разделив одно равенство на другое, получаем A’B/A’C=sinBAA’ /sinA’AC * (sinBCA/sinABC )

Записав аналогичные равенство для остальных отрезков и перемножив их, получаем условие Чевы в форме синусов.

Источник

Теорема Чевы

Муниципальная научно-практическая конференция

Автор: Панкова Вера, учащаяся 9 «Б» класса

, учитель математики МБОУ СОШ №17.

Данная работа может помочь ученикам различных образовательных учреждений расширить представление о свойствах треугольника с помощью теоремы Чевы. В работе систематизированы задачи на применение теоремы Чевы для доказательства свойств замечательных точек треугольника, для обоснования некоторых преобразований плоскости, для решения задач на отыскание набольших и наименьших значений величин, а также задач разного уровня сложности. Работа может быть использована для проведения занятий на элективных курсах, при подготовке к олимпиадам, ЕГЭ и вступительным экзаменам.

В настоящее время в современной школе роль геометрии несколько занижена. Данная работа может оказать помощь в укреплении престижа школьного предмета геометрии, т. к. показывает, как всего лишь одна замечательная теорема позволяет открыть целый пласт интереснейших свойств треугольника, насладиться красотой и изяществом решаемых с её помощью задач.

В ходе работы автор, Панкова Вера, проявила большую степень самостоятельности. Используя метод анализа и сравнения имеющихся источников литературы, автор столкнулась с необходимостью использовать ещё один метод исследования – систематизация задач. В используемой литературе задачи предлагаются списком без системы по определённым темам. Тематическая же систематизация задач значительно упростила возможности отыскания приёмов решения задач. При этом большая часть задач решена Верой самостоятельно, что способствовало повышению уровня логической культуры и развитию пространственного воображения автора.

Работа может быть использована для занятий на спецкурсах, в профильном обучении, при подготовке к олимпиадам и ЕГЭ.

Работа по теме «Теорема Чевы» посвящена исследованию возможностей применения теоремы Чевы, которая не входит в программу по геометрии средней школы. Тема является актуальной, так как при решении целого класса задач, теорема Чевы позволяет легко и изящно получать решения, тогда как, традиционные подходы приводят к громоздким и утомительным доказательствам.

В центре внимания находится доказательство самой теоремы разными способами и в разных формах.

В практической части проведено сравнение традиционных способов доказательства того, что три прямые пересекаются в одной точке, и доказательств с помощью теоремы Чевы.

Главные усилия направлены на решение задач с применением теоремы и их тематическую систематизацию, позволяющую упростить поиск приёмов решения. При этом автор решает, по существу, одну задачу: показывает преимущества использования теоремы Чевы для облегчения решения задач.

Необходимо остановиться на том, что при исследовании возможностей применения теоремы Чевы, автору удалось углубить знания о замечательных точках треугольника и дополнить, известные в школьном курсе четыре замечательные точки, новыми точками и точками второго порядка, т. е. полученными в результате преобразований. Рассмотренные преобразования также являются углублением школьного курса.

Достоинством данной работы является научность, доказательность, логическая последовательность в изложении материала.

« »……………..2007 г. Руководитель

а) Теорема Чевы и замечательные точки треугольника.……………..14

б) Точки Жергона и Нагеля и теорема Чевы ………………………….17

в) Некоторые замечательные преобразования, связанные с теоремой Чевы …………………………………………………………………….19

г) Применение теоремы Чевы к решению разных задач …………….23

д) Задачи на отыскание наибольших и наименьших значений величин, связанные с теоремой Чевы ……………………………………………26

1) Первая часть работы – теоретическая. Здесь представлены различные способы доказательства прямой и обратной теоремы Чевы: доказательство с помощью подобных треугольников, два доказательства с использованием понятия площади и теорема Чевы в форме синусов. Также здесь даются определение чевиан, как отрезков, соединяющих вершину треугольника с некоторой точкой на противоположной стороне треугольника и понятие конкурентности.

2) Вторая часть работы – практическая. Здесь приведена тематическая систематизация задач на применение теоремы Чевы. Все задачи сопровождаются решениями.

а) Теорема Чевы и замечательные точки треугольника. В этой главе с помощью теоремы Чевы доказывается конкурентность замечательных линий треугольника: медиан, биссектрис, высот и серединных перпендикуляров.

б) Точки Жергона и Нагеля. С помощью теоремы Чевы здесь доказывается, что прямые, проходящие через вершины треугольника и точки касания вписанной окружности, пересекаются в одной точке (точке Жергонна), а также, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля).

в) Некоторые замечательные преобразования, связанные с теоремой Чевы. В этой главе доказывается с помощью теоремы Чевы существование изотомически сопряжённой, изогонально сопряжённой к точке пересечения чевиан относительно треугольника точки, изоциркулярного образа точки пересечения чевиан. А также приведены примеры замечательных точек 2-го порядка, т. е. полученных с помощью указанных преобразований плоскости.

г) Применение теоремы Чевы к решению разных задач. Здесь приведены задачи с решениями разного уровня сложности, которые могут использоваться для самоконтроля.

д) Задачи на отыскание наибольших и наименьших значений величин, связанные с теоремой Чевы. В этой главе решены задачи на нахождение наибольших и наименьших значений величин элементарными методами, т. е. без применения производной.

Обладая литературой более обширной,

чем алгебра и арифметика вместе взятые,

и, по крайней мере, столь же обширной

как и анализ, геометрия в большей степени,

чем любой другой раздел математики,

является богатейшей сокровищницей

интереснейших, но полузабытых вещей,

которыми, спешащее поколение

не имеет времени насладиться.

Крылатую фразу Козьмы Пруткова «Никто не обнимет необъятного» в полной мере можно отнести к геометрии треугольника. Треугольник, как кладезь прекрасных и поразительных геометрических конструкций, поистине неисчерпаем. Их пестрота и изобилие, с трудом поддающиеся какой-либо систематизации, не могут не восхищать.

Геометрия треугольника связана, как правило, с замечательными точками. Большинство же замечательных точек может быть получено следующим образом.

Пусть имеется некоторое правило, по которому можно выбрать точку А1 на стороне ВС треугольника АВС (например, выберем середину этой стороны). Затем построим аналогичные точки В1, С1 на двух других сторонах треугольника (в нашем примере – еще две середины сторон). Если это правило «удачное», то прямые АА1, ВВ1, СС1 пересекутся в некоторой точке Z. Ученым прошлого всегда хотелось иметь метод, позволяющий по положению точек на сторонах треугольника определять, пересекается ли соответствующая тройка прямых в одной точке или нет.

Универсальное условие, «закрывшее» эту проблему, нашел в 1678г. итальянский инженер Джованни Чева.

Замечательная теорема Чевы не входит в программу по геометрии для средней школы. Однако при решении целого класса задач эта теорема позволяет легко и изящно получать решения. Теорема Чевы открывает возможности для знакомства со многими новыми теоремами и свойствами треугольника, не изучаемыми по школьной программе.

Цель работы: расширить представление о свойствах треугольника с помощью теоремы Чевы.

Гипотеза: если теорема Чевы помогает расширить класс решаемых геометрических задач, то она является одной из фундаментальных теорем геометрии.

· исследовать возможности применения теоремы Чевы для доказательства свойств замечательных точек треугольника;

· научиться применять теорему Чевы для решения задач разного уровня сложности;

· тематически систематизировать задачи, решаемые с помощью теоремы Чевы.

Методы исследования: анализ и сравнение имеющихся источников литературы, систематизация задач.

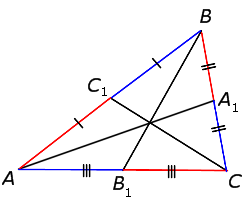
Отрезок, соединяющий вершину треугольника с некоторой точкой на противоположной стороне, называется ЧЕВИАНОЙ.

АХ, ВY, СZ – чевианы ∆ АВС.

Если все три чевианы пресекаются в одной точке Р, то будем говорить, что они КОНКУРЕНТНЫ.

1) Теорема Чевы. Если три чевианы АХ, ВY, СZ треугольника АВС конкурентны, то

Доказательство. Известно, что площади треугольников с равными высотами пропорциональны основаниям треугольников.

.

.

Перемножим, полученные равенства

.

Если три чевианы АХ, ВY, СZ удовлетворяют соотношению , то они конкурентны.

Предположим, что две первые чевианы пересекаются в точке Р, как и прежде, а третья чевиана, проходящая через точку Р, будет СZ’.

Тогда, по прямой теореме Чевы,

.

Но по условию ,

Следовательно, .

Точка совпадает с точкой Z, и мы доказали, что отрезки АХ, ВY и СZ конкурентны.

2) Рассмотрим способ доказательства теоремы Чевы с помощью подобных треугольников[4].

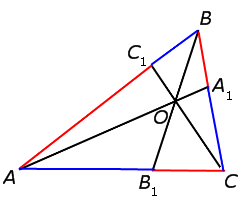
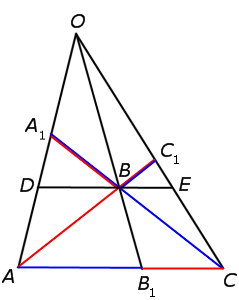
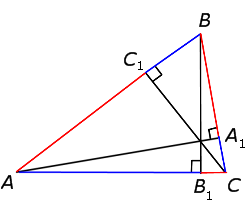
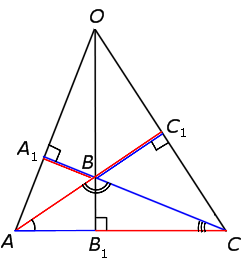
Пусть на сторонах AB, BC и AC треугольника ABC взяты соответственно точки C1, A1 и B1. Прямые AA1, BB1, CC1 пересекаются в одной точке тогда и только тогда, когда

(*)

Доказательство. Предположим, что

прямые AA1, BB1, CC1 пересекаются в точке O (рис.2). Через вершину C треугольника ABC проведем прямую, параллельную AB, и ее точки пересечения с прямыми AA1, BB1 обозначим соответственно A2, B2. Из подобия треугольников CB2B1 и ABB1 имеем равенство

(1)

Аналогично, подобия треугольников BAA1 и CA2A1 имеем равенство

(2)

Далее, из подобия треугольников BC1O и B2CO, AC1O и A2CO имеем Следовательно, имеет место равенство

(3)

Перемножая равенства (1), (2) и (3), получим требуемое равенство (*).

Докажем обратное. Пусть для точек A1, B1, C1, взятых на соответствующих сторонах треугольника ABC выполняется равенство (*). Обозначим точку пересечения прямых AA1 и BB1 через O и точку пересечения прямых CO и AB через C‘. Тогда, на основании доказанного, имеет место равенство

Учитывая равенство (*), получим равенство из которого следует совпадение точек C‘ и C1 и, значит, прямые AA1, BB1, CC1 пересекаются в одной точке.

3) Ещё один способ доказательства теоремы Чевы, использующий понятие площади.[4]

Предположим, что прямые АА1, ВВ1, СС1 пересекаются в точке О. (рис.3) Опустим из вершин А и В треугольника АВС перпендикуляры АА’, ВВ’ на прямую СС1. Треугольники АС1А’ и ВС1В’ подобны, следовательно,

Перемножая полученные равенства, получаем

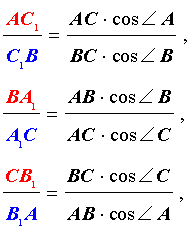
4) Теорема Чевы в форме синусов

Выберем в произвольном треугольнике АВС точки А1, В1, С1 на сторонах ВС, СА, АВ соответственно, тогда условие Чевы можно записать также в виде

Применим теорему синусов к треугольникам АСС1 и ВСС1(рис.4), имеем

Умножив одно равенство на другое, получаем:

и

Окончательно имеем:

а) Теорема Чевы и замечательные точки треугольника.

Теорема Чевы дает возможность очень просто доказать утверждения о точке пересечения медиан, биссектрис, высот (или их продолжений) и средних линий треугольника.

Медианы – это чевианы, которые связывают вершины треугольника с серединами противоположных сторон.

Задача №1. Доказать, что медианы треугольника конкурентны.

Доказательство. Так как AB1 = B1C; СА1 = А1В (рис.5);

ВС1 = С1А, то

.

По теореме Чевы отсюда следует, что медианы конкурентны.

Высоты – это чевианы, перпендикулярные сторонам или продолжениям сторон треугольника.

Их общая точка называется ортоцентром.

Применение теоремы обратной теореме Чевы для доказательства того, что три прямые пересекаются в одной точке, существенно упрощает доказательство. Сравним доказательство конкурентности высот треугольника, проводимое с помощью теоремы Чевы и доказательство другим способом.

Задача №2. Доказать, что высоты остроугольного треугольника, конкурентны.

Доказательство. Пусть АА1, ВВ1 и СС1 – высоты треугольника. (рис.6) Прямоугольные ∆ АА1С и ∆ВВ1С подобны (так как имеют общий острый угол С), поэтому

Аналогично из подобия ∆ АА1В и ∆СС1В следует:

А из подобия ∆ ВВ1А и ∆СС1А – равенство.

Перемножив все три равенства, получим:

По теореме Чевы следует, что высоты остроугольного треугольника пересекаются в одной точке, т. е. конкурентны.

Докажем, что три высоты треугольника пересекаются в одной точке.

* http://geometr. info/geometriia/treug/medvys. html

Очевидно, теорема Чевы облегчает доказательство.

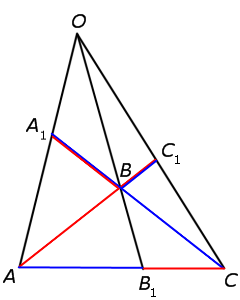
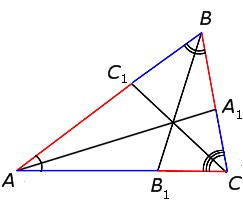
Задача №3. Доказать, что биссектрисы треугольника пересекаются в одной точке, т. е. конкурентны.

Доказательство.

Пусть АА1, ВВ1 и СС1 – биссектрисы ∆ АВС (рис.8)

Воспользуемся тем, что биссектриса треугольника делит противоположную сторону на

Рис.8 отрезки, пропорциональные

прилежащим сторонам. Согласно этому свойству

Перемножив эти равенства, получим:

Отсюда по теореме Чевы следует, что биссектрисы пересекаются в одной точке.

Четвертой замечательной точкой треугольника является точка пересечения серединных перпендикуляров к сторонам треугольника.

Серединным перпендикуляром к отрезку

называется прямая, проходящая через середину отрезка и перпендикулярная к нему (рис.9)

Задача№4. Доказать, что серединные перпендикуляры к сторонам треугольника конкурентны.

Доказательство.

Рассмотрим ∆АВС, А1,В1иС1 – соответственно середины сторон ВС, СА и АВ.(рис.10)

Но теорема Чевы создана для выявления

конкурентности чевиан, а не перпендикуляров к сторонам треугольника. Это затруднение можно

преодолеть, рассмотрев серединный треугольник А1В1С1. Поскольку средние линии параллельны сторонам исходного треугольника, то серединные перпендикуляры являются высотами серединного треугольника, конкурентность которых была уже доказана с помощью теоремы Чевы. Это означает, что серединные перпендикуляры к сторонам ∆ АВС конкурентны. Теорема доказана.

б) Точки Жергона и Нагеля и теорема Чевы.

Воспользуемся теоремой Чевы для установления еще двух замечательных точек треугольника.

Задача№5 Доказать, что прямые, проходящие через вершины треугольника и точки касания вписанной окружности, пересекаются в одной точке, называемой точкой Жергона.

Доказательство.

Пусть окружность с центром О касается сторон ∆АВС в точках А1, В1, С1 (рис.11) тогда по свойству отрезков касательных, проведенных к окружности из одной точки.

АВ1 = АС1; ВС1 = ВА1; СА1 = СВ1

Рис.11

,

Значит. Прямые АА1, ВВ1, СС1 конкурентны, т. е. пересекаются в одной точке G – точка Жергона.

Еще одна замечательная точка треугольника – точка Нагеля.

Определение. Окружность называется вневписанной в треугольник, если она касается одной стороны этого треугольника и продолжений двух других его сторон.

Задача№6 Доказать, что прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей, пересекаются в одной точке (точке Нагеля).

Пусть АВ = с; ВС = а; АС = b; по свойству равенства отрезков касательных ВХb = BZb.(рис.12)

ВХb + BZb = ВС + СХb + ZbA + AB,

СХb + ZbA = b,

ВХb + BZb = а +b +с = 2p (p – полупериметр треугольника),

ВХb = BZb.= p, аналогично, для отрезков касательных, проведенных из других двух вершин. Также СХb = ВХb – ВС = p-a; для всех отрезков касательных можно также записать

ВХc = BZc = CXb = CYb = p-a,

CYa = CXa = AYc = AZc = p-b,

AZb = AYb = BZa = BXa = p-c.

Проверим условие Чевы.

.

Следовательно, по теореме Чевы прямые, проходящие через вершины треугольника и точки касания вневписанных окружностей со сторонами треугольника конкурентны.

в) Некоторые замечательные преобразования, связанные с теоремой Чевы

Теорема Чевы позволяет получать и другие замечательные точки треугольника. Для этого нужно рассмотреть некоторые преобразования, связанные с теоремой Чевы.

Зафиксируем на плоскости треугольник АВС.

Выберем некоторую точку плоскости Z (рис.13) и

проведём через неё и вершины треугольника

прямые, пересекающие стороны треугольника

в точках А1,В1,С1 соответственно.

Каждую такую точку отразим

симметрично относительно

середины той стороны, на

которой она лежит. Полученные три точки обозначим через А2, В2, С2. Доказать, что тогда прямые АА2, ВВ2,СС2 также пересекаются в некоторой точке Zm.

Доказательство. По теореме Чевы т. к. АА1, ВВ1,СС1 пересекаются в одной точке, то

но А2 и А1, В2 и В1, С2 иС1 симметричны относительно середин сторон треугольника, => АС1=ВС2 ; С1В=АС2 ; ВА1=СА2 и т. д.

поэтому , => АА2, ВВ2,СС2

пересекаются в одной точке.

Эта точка называется изотомически сопряжённой точке Z, относительно треугольника АВС.

Задача№8

Зафиксируем на плоскости треугольник АВС. Вновь выберем некоторую точку плоскости Z и проведём через неё и вершины треугольника прямые, пересекающие стороны треугольника в точках А1,В1,С1 соответственно.(рис.14) Доказать, что прямые АА2, ВВ2,СС2, симметричные прямым АА1, ВВ1,СС1 относительно биссектрис соответствующих углов треугольника, пересекаются в одной точке Z1.

Доказательство. Здесь удобно воспользоваться теоремой Чевы в форме синусов.

,=> т. к. прямые АА2, ВВ2,СС2, симметричны прямым АА1, ВВ1,СС1 относительно биссектрис соответствующих углов треугольника, то равны углы =

=>

прямые АА2, ВВ2, СС2 тоже пересекаются в одной точке.

Эта точка называется изогонально сопряжённой точке Z относительно треугольника АВС.

С помощью изотомического и изогонального сопряжений можно получать новые замечательные точки.

Hm – антиортоцентр – точка, изотомически сопряжённая ортоцентру, т. е. точка пересечения прямых, проходящих через точки, симметричные основаниям высот относительно середин сторон, и соответствующие вершины треугольника.( Рис.16)

Im– точка пересечения антибиссектрис – точка изотомически сопряжённая центру вписанной в треугольник окружности.( Рис.17)

Gl – точка, изогонально сопряжённая точке Жергонна.( Рис.18)

Nl – точка, изогонально сопряжённая точке Нагеля.( Рис.19)

Возьмём точку Z внутри треугольника АВС. Пусть прямая АZ пересекает

описанную окружность в точке А1.

В сегмент, отсекаемый стороной ВС, впишем окружность, касающуюся дуги ВС в точке А1, а стороны ВС – в точке А2. Аналогично определим точки В2 и С2. Доказать, что прямые АА2, ВВ2, СС2 пресекаются в одной точке Zc.( Рис. 20)

Докажем, что прямые АА2, ВВ2,СС2 пересекаются в одной точке с помощью теоремы Чевы сразу в двух формулировках – в форме отношений синусов и в форме отношений отрезков, а также с помощью леммы.

Лемма Архимеда. Если окружность вписана в сегмент и касается дуги в точке А1, а хорды ВС – в точке А2, то прямая А1А2 является биссектрисой угла ВА1С.(стр.15 [5])

Доказательство. Пусть ∟ВАА1=α1, ∟САА1=α2. Поскольку А1А2 – биссектриса угла при вершине А1 треугольника ВА1С, то по свойству биссектрисы , а т. к. треугольники ВАА1 и САА1 вписаны в одну и ту же окружность, по теореме синусов ВА1=2R sin α1, CA1=2R sin α2, =>

Аналогично получаем, что ,

где β1=∟СВВ1, β2=∟АВВ1, γ1=∟АСС1, γ2=∟ВСС1. Условие Чевы для прямых АА2, ВВ2,СС2, таким образом, принимает вид

Правая часть этого равенства представляет собой выражение из условия Чевы в форме отношений синусов для прямых АА1, ВВ1,СС1, пересекающихся в точке Z. Следовательно,

Т. о. прямые АА2, ВВ2, СС2 пресекаются в одной точке Zc, которую и называют изоциркулярным образом точки Z.

г) Применение теоремы Чевы к решению разных задач

Задача№10 Точки С1 и А1 делят стороны АВ и ВС ∆ АВС в отношении 1:2.

прямые СС1 и АА1 пересекаются в точке О. Найдите отношение, в котором

прямая ВО делит сторону АС. [4]

По теореме Чевы, если прямые конкурентны, то

Задача№11 На сторонах ВС, СА и АВ ∆ АВС взяты точки А1, В1 и С1 так, что отрезки АА1, ВВ1 и СС1 пересекаются в одной точке. Прямые А1В1 и А1С1 пересекают прямую, проходящую через вершину А параллельно стороне ВС, в точках С2 и В2 соответственно. Докажите что АВ2 = АС2. [ 2]

∆АС2С1

получили условие Чевы

АВ2 = АС2

Задача№12 Доказать, что в произвольном треугольнике прямые, проходящие через вершины и делящие периметр треугольника пополам, пересекаются в одной точке. [2].

Доказательство.

Рассмотрим ∆АА1С и ∆СС1А, у них АС – общая, а так как

АС1 + АС = АС + А1С = Р,

Аналогично, можно получить остальные равенства. Проверим условие Чевы

данные прямые конкурентны.

Задача№13 На стороне АС треугольника АВС взяты точки Р и Е, на стороне ВС – точки М и К, причем АР:РЕ:ЕС = СК:КМ:МВ. Отрезки АМ и ВР пересекаются в точке О, отрезки АК и ВЕ – в точке Т. Докажите, что точки О, Т и С лежат на одной прямой.

Дано: АР:РЕ:ЕС = СК:КМ:МВ

Доказать: О, Т и С – лежат на одной прямой.

По теореме Чевы:

(1) (2)

Таким образом, с помощью теоремы Чевы, из (1) и (2) следует, что т. С1 и С2 делят отрезок АВ в одном и том же отношении и следовательно, совпадают.

д) Задачи на отыскание наибольших и наименьших значений величин, связанные с теоремой Чевы.

Теорема Чевы открывает возможность решать некоторые задачи на отыскание наибольших и наименьших значений элементарными методами.

Задача№14 Найти внутри треугольника такую точку О, чтобы произведение

АВ1• ВС1•СА1 имело наибольшую величину (А1, В1, С1 – точки пересечения прямых АО, ВО, СО со сторонами ВС, СА, АВ).

Проведём медианы АА2, ВВ2, СС2, пересекающиеся в точке М. Так как средняя геометрическая двух величин не больше их средней арифметической, то

Возводя в квадрат, каждое из полученных неравенств и перемножая квадраты, получим:

АВ1• В1С•СА1• А1В• ВС1•С1А ≤ (АВ2•ВА2•АС2)2.

Так как АВ1•СА1•ВС1=В1С•А1В•С1А, то

Неравенство обращается в равенство в случае совпадения оснований прямых Чевы с серединами соответствующих сторон; следовательно, в этом случае произведение

АВ1•СА1•ВС1 имеет наибольшую величину, равную , где а, в,с –стороны треугольника. Искомой точкой является точка пересечения медиан треугольника.

Задача№15 Для каждой из чевиан, пересекающихся внутри треугольника, выполняется соотношение называемое отношением Чевы.

Другими словами, отношение Чевы равно сумме отношений отрезков, отсечённых двумя другими чевианами на прилежащих сторонах, считая эти отрезки от вершины. Эту задачу ещё называют теоремой Ван-Обеля [4]

Проведём через вершину А прямую, параллельную основанию ВС, до пересечения её с продолжениями чевиан ВВ1 и СС1 соответственно в точках В2 и С2. Из подобия треугольников АМВ2 и ВМА1 имеем:

Из подобия треугольников АМС2 и СМА1 имеем: Следовательно

По свойству равных отношений имеем:

Или (1)

Из подобия треугольников АС1С2 и ВС1С получаем:

Из подобия треугольников АВ2В1 и ВВ1С находим:

Следовательно, (2)

Из сравнения равенств (1) и (2) получаем:

1) Пусть точка М – точка пересечения медиан, тогда

2) Пусть точка М – точка пересечения биссектрис, тогда

Задача№16 Найти внутри треугольника точку М, для которой сумма отношений Чевы для проходящих через неё прямых была бы наименьшей.

Запишем отношения Чевы:

Каждая из сумм, стоящих в скобках является суммой двух взаимно обратных величин, эта сумма не менее двух (задача 77 [6]), то

Наименьшее значение, равное 6, может получиться, если точка М есть точка пересечения медиан.

Задача№17 Разность между произведением трёх отношений Чевы и суммой их постоянна и равна 2.

()()()=λаλвλс+λа+λв+λс+

=

Задача№18 Найти внутри треугольника точку М, для которой произведение отношений Чевы для проходящих через неё чевиан было бы наименьшим.

С помощью задачи №16 понятно, что наименьшее произведение отношений равно 8, а искомая точка – точка пересечения медиан.

Задача№19 Если прямые АА1, ВВ1,СС1, выходящие из вершин треугольника АВС, пересекаются в точке М, внутри треугольника, то

Так как площади АМС и АВС относятся

как их высоты, а последние относятся как , то

. Аналогично .

Сложив найденные равенства, получим:

Докажем теперь второе равенство. Так как

И точно также , то 3 – () =2.

Задача№20 Сумма обратных величин высот треугольника равна обратной величине радиуса вписанного круга, т. е. .

Действительно

Но , а поэтому

Задача№21 Из всех треугольников, описанных около данного круга, равносторонний имеет наименьшее произведение высот.

В равностороннем треугольнике ha=hb=hc. Из соотношения

Можно заключить, что имеет наибольшее значение при

Следовательно, ha•hb•hc имеет наименьшее значение при

Приведённые в данной работе доказательства и решения задач показывают огромное значение теоремы Чевы как метода, позволяющего по положению точек на сторонах треугольника определять, пересекается ли соответствующая тройка прямых в одной точке или нет. Кроме того, работа над применением теоремы Чевы открывает возможность для знакомства со многими новыми свойствами и понятиями геометрии треугольника. Это подтверждает предположение о том, что теорема Чевы является одной из фундаментальных теорем геометрии. Думаю, работа будет интересна не только для меня, но и для учащихся, занимающихся математикой на профильном уровне.

2. «Задачи по планиметрии», часть 1, М. Наука, 1986.

4. «Геометрия на профильном уровне», Издательский дом «Первое сентября» Математика. ЕУМГ №17 2006.

5. «Элементы геометрии треугольника», библиотека «мат. просвещ.», издательство МЦНМО Москва 2002г.

6. «Задачи на максимум и минимум», ОГИЗ, Москва, 1948, Ленинград.

Источник