Доказать что число 915 327 делится на 26

Диагностическая работа 10 класс «Делимость чисел»

(Алгебра 10 класс, УМК Колягин и др.)

Не выполняя деления, найти остаток от деления числа 485638 на 5

Найти действительные корни уравнения:

Доказать, что число 9 15 – 3 27 делится на 26.

Найти все целочисленные решения уравнения: а) 26 х + 39 у = 15;

Не выполняя деления, найти остаток от деления числа 728362 на 5

Найти действительные корни уравнения:

Доказать, что число 2 36 + 4 16 делится на 17

Найти все целочисленные решения уравнения: a ) 5 х + 3 у = 17;

(Алгебра 10 класс, УМК Колягин и др.)

Не выполняя деления, найти остаток от деления числа 874569 на 5

Найти действительные корни уравнения:

Доказать, что число 25 6 + 5 13 делится на 30.

Найти все целочисленные решения уравнения: a ) 7 х – 9 у = 23;

Не выполняя деления, найти остаток от деления числа 567893 на 5

Найти действительные корни уравнения:

Доказать, что число 16 10 – 2 35 делится на 31.

Найти все целочисленные решения уравнения: : а) 36 х + 45 у = 11;

а) нет решения; b ) (7, 6); (-7,-6); (-7,6);(7,-6).

(2 36 +4 16 ):17=(2 36 +2 32 ):17=2 32 (2 4 +1):17=2 32

(25 6 +5 13 ) : 6= (5 12 +5 13 ):6=5 12 (1+ 5):6=5 12

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-760530

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В России планируют создавать пространства для подростков

Время чтения: 2 минуты

В России утверждены новые аккредитационные показатели для школ и колледжей

Время чтения: 2 минуты

В Ленобласти педагоги призеров и победителей олимпиады получат денежные поощрения

Время чтения: 1 минута

Минпросвещения сформирует новый федеральный перечень учебников

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Контрольная работа №1 Вариант-1 1.Найдите остаток от деления числа 485638 на 5, не выполняя деления

Контрольная работа №1

1.Найдите остаток от деления числа 485638 на 5, не выполняя деления.

2.Найдите последнюю цифру числа 317+425.

3.Доказать, что число 915-327 делится на 26.

4.Натуральные числа 8n+1 и 5n+2 делятся на натуральное число m≠1.

5.Доказать, что уравнение 26х+39у =15 не имеет целочисленных решений.

6.Доказать, что уравнение х2- у2= 230 не имеет целочисленных решений.

Найдите остаток от деления числа 728362 на 4, не выполняя деления. Найдите последнюю цифру числа 963+239. Доказать, что число 236-416 делится на 17. Натуральные числа 6n+5 и 7n+5 делятся на натуральное число m≠1.

5.Доказать, что уравнение 36х+45у =11 не имеет целочисленных решений.

Контрольная работа №2

1.Выполнить деление многочлена х4+ 3х3-21х2-43х+60 на многочлен

2.Не выполняя деления, найти остаток от деления многочлена х4+х3+7х2+х+3 на двучлен(х-2).

4.Найти член разложения бинома

( х2-)15, не содержащий х.

6.Решить систему уравнений

1.Выполнить деление многочлена х4- 9х3+х2+ 81х+70 на многочлен

2. Не выполняя деления, найти остаток от деления многочлена

2х4-х3- 2х2+3х на двучлен(х-1).

4.Найти член разложения бинома

(2 х2-)10, не содержащий х.

6.Решить систему уравнений

Контрольная работа №3

Степень с действительным показателем

1) 1)

2) 2)

2. Упростить выражение при

1) 1)

2) 2)

3. Сократить дробь 3. Сократить дробь

1) 1)

2) и 1. 2) и 1.

5. Найти сумму бесконечно убывающей геометрической прогрессии,

если

5. Найти второй член бесконечно убывающей геометрической прогрессии, если сумма её членов равна , а знаменатель равен

Контрольная работа №4

1. Найти область определения функции .

2. Изобразить эскиз графика функции у = х7 и перечислить её основные свойства. Пользуясь свойствами этой функции:

1) сравнить с единицей (0,95)7;

2) сравнить и .

3. Решить уравнение:

1) 2) .

3)

4. Установить, равносильны ли неравенства и

4. Решить неравенство: 1) ; 2)

5. Решить систему уравнений

6. (Дополнительно) Решить уравнение

1. Сравнить числа: 1) и ; 2) и .

2. Решить уравнение: 1) ; 2)

3. Решить неравенство .

4. Решить неравенство: 1) ; 2)

5. Решить систему уравнений

6. (Дополнительно) Решить уравнение

Контрольная работа № 6 Логарифмическая функция

2. Сравните числа и

3. Решите уравнение

4. Решите неравенство

5. Решите уравнение

6. Решите неравенство:

2. Сравните числа и

3. Решите уравнение

4. Решите неравенство

5. Решите уравнение

6. Решите неравенство:

Контрольная работа №7

Тригонометрические формулы Вариант 1

Найти значение выражения:

1) 2) 3)

2. Вычислить:

3. Упростить выражение:

4. Доказать тождество:

5. Решить уравнение

1. Найти значение выражения:

1) 2) 3)

2. Вычислить:

3. Упростить выражение:

4. Доказать тождество:

5. Решить уравнение

5. Решить уравнение

Контрольная работа № 8

1. Решите уравнение:

2. Найдите решение уравнения на отрезке .

3. Решите уравнение:

; в)

4. Решите уравнение:

а)

1. Решите уравнение:

а)

2. Найдите решение уравнения на отрезке .

3. Решите уравнение:

в)

4. Решите уравнение:

а)

Источник

Доказать что число 915 327 делится на 26

Задача 15:

Найдите остатки от деления

а) 1989 • 1990 • 1991 + 1992³ на 7;

Решение:

Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.

Задача 16:

Докажите, что n³ + 2n делится на 3 для любого натурального n.

Решение:

Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.

Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.

Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.

Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.

Задача 17:

Докажите, что n 5 + 4n делится на 5 при любом натуральном n.

Решение:

Указание: Переберите остатки от деления на 5.

Задача 18:

Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 3.

Задача 19:

Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.

Решение:

Переберите остатки от деления на 9.

Задача 20:

Докажите, что n³ – n делится на 24 при любом нечетном n.

Решение:

Указание: Докажите, что указанное число делится и на 3, и на 8.

Задача 21:

а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.

б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.

Решение:

Указание: Докажите, что указанные числа делятся и на 3 и на 8.

Задача 22:

Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.

Решение:

Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.

Задача 23:

a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.

Решение:

Проверьте, что и a и b делятся и на 3 и на 7.

Задача 24:

a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.

Решение:

Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.

Задача 25:

Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.

Решение:

Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.

Задача 26:

Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.

Решение:

Выясните возможные остатки квадратов при делении на 8.

Задача 27:

Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.

Решение:

Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.

Задача 28:

Решение:

Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 • 9 = 81), а за 1 – 9 (1 • 9 = 9).

Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.

Задача 29:

Решение:

Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.

Задача 30:

Решение:

Задача 31:

Найдите остаток от деления 2¹ºº на 3.

Решение:

Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».

Задача 32:

Найдите остаток от деления 3 1989 на 7.

Решение:

Задача 33:

Докажите, что 2222 5555 + 5555²²²² делится на 7.

Решение:

Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.

Задача 34:

Найдите последнюю цифру числа .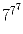

Задача 35:

а) p, p + 10, p + 14 – простые числа. Найдите p.

б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.

Решение:

Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.

Задача 36:

p и 8p² + 1 – простые числа. Найдите p.

Решение:

Задача 37:

p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.

Решение:

Задача 38:

Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.

Решение:

Рассмотрите остатки по модулю 3.

Задача 39:

а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?

б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 40:

Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.

Решение:

Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.

Задача 41:

p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.

Ответ: p = 5. Рассмотрите остатки при делении на 5.

Задача 42:

Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.

Решение:

Это число дает остаток 7 от деления на 9.

Задача 43:

Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.

Решение:

Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.

Задача 44:

Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.

Решение:

Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.

Задача 45:

x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.

Решение:

Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.

Источник