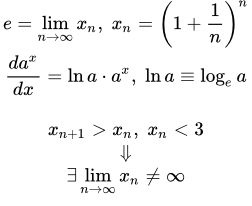Доказать что число является пределом

Доказать что число является пределом

`|x_n-a| oo) x_n=a` (читается: предел `x_n` при `n`, стремящемся к бесконечности, равен `a`). Последовательность, называется сходящейся, если существует число `a`, являющееся её пределом. Если такого числа `a` не существует, то последовательность называется расходящейся.

Часто в определении предела полагают число `k` натуральным. Однако, как нетрудно понять, получится эквивалентное определение.

Пусть выбрано произвольное `epsilon>0`. Нам нужно найти такое число `k`, что при всех `n>k` выполнялось бы неравенство `|x_n-c| k` имеет место неравенство `|x_n-c| oo)x_n=c`.

В разобранном примере число `k` удалось выбрать так, чтобы оно годилось сразу для всех `epsilon`. Такой случай не типичен.

Доказать, что `lim_(n->oo)1/n=0`.

Могут ли два разных числа быть пределами одной и той же последовательности?

Пусть `lim_(n->oo)x_n=a`. Имеет ли предел последовательность `(x_(n+1))`?

Пусть `lim_(n->oo)x_n=a`, `epsilon>o`. Можно ли утверждать, что найдётся такое число `k`, что `|x_n-a| k`?

Да. Поскольку `lim_(n->oo)x_n=a`, то по определению предела для любого положительного числа `alpha`, а следовательно, и для `alpha=epsilon//2`, найдётся число `k`, такое что `|x_n-a|k`.

Сформулируем необходимое условие существования предела.

Если последовательность имеет предел, то она ограничена.

Доказать, что последовательность `x_n=(-1)^n` не имеет предела.

Предположим противное, т. е. какое-то число `a` является пределом этой последовательности. Тогда для `epsilon=1` найдётся такое число `k`, что `|x_n-a| k`. Пусть номер `N>k`, тогда `|x_N-a| oo)y_n!=0`). При этом

Ограничимся доказательством пункта 2. Фиксируем произвольное `epsilon>0`. Нам нужно показать, что существует такое число `k`, что `|x_ny_n-ab| k`. По теореме 2.1 последовательности `(x_n)` и `(y_n)` ограничены; тем самым найдётся такое `C>0`, что `|x_n| k_1`, а также число `k_2` такое, что `|y_n-b| k_2`. Если положить `k=max`, то при `n>k` имеем:

`|x_ny_n-ab| oo)cx_n=clim_(n->oo)x_n` для любого `cinR`.

В самом деле, рассмотрим последовательность `y_n=c`. Поскольку `lim_(n->oo)y_n=c` (пример 2.1), то по пункту 2 теоремы 2.2

Показать, что `lim_(n->oo) 1/(n^2)=0`.

Поскольку `lim_(n->oo) 1/n=0`, то по пункту 2 теоремы 2.2

`lim_(n->oo) 1/(n^2)=lim_(n->oo) 1/n*lim_(n->oo) 1/n=0`.

Теорему 2.2 можно обобщить на произвольное (конечное) число слагаемых (сомножителей). В частности, `lim_(n->oo)1/n^m=0` для любого `m inN`.

Обозначим дробь, стоящую под знаком предела, через `x_n`. В числителе и знаменателе `x_n` стоят последовательности, не являющиеся ограниченными (доказывается аналогично примеру 1.6). По теореме 2.1 они не имеют предела и теорема о пределе частного (теорема 2.2 3)) «напрямую» здесь неприменима. Поступим следующим образом: поделим числитель и знаменатель на наибольшую степень `n`. По формулам сокращённого умножения `(n+2)^3-n(n-1)^2=8n^2+11n+8`, так что `x_n` можно переписать в виде:

Теперь в числителе и знаменателе `x_n` стоят сходящиеся последовательности:

По пункту 3 теоремы 2.2

Следующее полезное свойство пределов известно под названием теоремы о «зажатой» последовательности.

Для данного `epsilon>0` существует такое число `k_1`, что члены `x_n` лежат в интервале `(a-epsilon, a+epsilon)` при всех `n>k_1`, и существует такое число `k_2`, что члены `z_n` лежат в интервале `a-epsilon;a+epsilon)` при всех `n>k_2`. Положим `k=max`. Тогда при `n>k` одновременно `x_n in(a-epsilon;a+epsilon)` и `z_n in(a-epsilon;a+epsilon)` и, следовательно, `a-epsilon oo)x_n=1`.

Попробуем «зажать» `x_n` между членами последовательностей, сходящихся к одному и тому же числу, и применим теорему 2.3.

`sqrt(n^2+n) 1/(n+1) iff n/(sqrt(n^2+n))>n/(n+1)`.

Учитывая `n/(sqrt(n^2+1)) oo)n/(n+1)=1` и `lim_(n->oo)1=1`, по теореме 2.3 `lim_(n->oo)x_n=1`.

Если для любого `n inN`, `n>=n_0` выполняется неравенство `a_n oo)a_n=a`, `lim_(n->oo)b_n=b`, то `a b`. По определению предела для `epsilon=(a-b)/2` найдутся такие `k_1`, `k_2`, что для `n>k_1` выполняется `|a_n-a| k_2` выполняется `|b_n-b| k` имеем `b_n oo)1/n=0`.

В теории пределов важную роль играет следующий факт.

Всякая монотонная ограниченная последовательность имеет предел.

Эта теорема эквивалентна свойству полноты множества действительных чисел. Образно говоря, свойство полноты означает, что числовая ось является «сплошным» множеством, множеством без «дырок».

Источник

Определение предела последовательности. Свойства сходящихся последовательностей.

Числовые последовательности.

Если каждому натуральному числу n сопоставлено в соответствие некое число x_n, то говорят, что задана числовая последовательность

Как мы видим, x_n — это функция, множеством определения которой является множество N всех натуральных чисел, а множество значенией этой функции, то есть значение всех x_n, n∈N, называют множеством значений последовательности.

Множество значений последовательности может быть как конечным, так и бесконечным, но множество ее элементов всегда бесконечно, так как любые два разных элемента последовательности отличаются своими номерами.

Последовательность может быть задана формулой, которая позволяет вычислить каждый член последовательности по ее номеру. Например, если \(x_n=\frac<\left(-1\right)^n+1>2\), то каждый нечетный член последовательности будет равен 0, а каждый четный член равен 1.

Зачастую используют реккурентный способ записи формулы последовательности, когда каждый следующий член последовательности можно найти по известным предыдущим.

Определение предела последовательности.

Записать с помощью логических символов отрицания следующих утверждений:

Пользуясь определением: найти предел последовательности \(\\>\), если:

Пусть \(\displaystyle \lim_x_n=a,\ \lim_y_n=a\). Доказать, что последовательность
$$
x_<1>,\ y_<1>,\ x_<2>,\ y_<2>\ldots,\ x_, \ y_\ldots\label
$$
сходится и ее предел также равен a.

\(\triangle\) По определению предела для любого \(\varepsilon > 0\) существуют \(N_1=N_1(\varepsilon)\) и \(N_<2>=N_<2>(\varepsilon)\) такие, что для всех \(n\geq N_<1>\) выполняется неравенство \(|x_-a| N_<\varepsilon>\geq N_<1>\), и поэтому \(|z_-a|=|x_-a| Пример 4.

Таким образом, а—предел последовательности \(\left\\), если для каждой ε—окрестности точки а найдется номер, начиная с которого все члены последовательности принадлежат этой окрестности, так что вне этой окрестности либо нет ни одного члена последовательности, либо содержится конечное число членов.

С помощью логических символов данное определение можно записать следующим образом

Доказать, что последовательность \(\left\\), где \(x_n=(-1)^n\), является расходящейся.

Единственность предела последовательности.

Числовая последовательность может иметь только один предел.

Предположим, что \(\left\\) имеет два различных предела a и b, причем a Рис. 4.2

Выберем ε > 0 таким, чтобы ε—окрестности точек a и b не пересекались, то есть не имели общих точек. Возьмем, например, ε = (b − a)/3. Так как число a—предел последовательности <x_n>, то по заданному ε > 0 можно найти номер N такой, что \(x_n\in U_\varepsilon(a)\) для всех n > N. поэтому вне интервала \(U_\varepsilon(a)\) может оказаться лишь конечное число членов последовательности. В частности, интервал \(U_\varepsilon(b)\) может содержать лишь конечное число членов последовательности. Но это противоречит тому, что b—предел последовательности, так как согласно определению предела, любая окрестность точки b должна содержать бесконечное число членов последовательности. Данное противоречие показывает, что последовательность не может иметь два различных предела. Итак, сходящаяся последовательность имеет только один предел.

Ограниченность сходящейся последовательности.

Последовательность \(\left\\) называется ограниченной снизу, если существует такое число С₁, что все члены последовательности удовлетворяют условию \(x_n\geq C_1\), то есть

Последовательность \(\left\\) называется ограниченной сверху, если

Последовательность, ограниченная как сверху, так и снизу, называется ограниченной, то есть последовательность \(\left\\) называется ограниченной, если

$$ \exists \ C_1 \ \exists \ C_2: \ \forall n \ \in\mathbb \ \rightarrow C_1\leq x_n\leq C_2\label $$

Заметим, что условие \eqref равносильно следующему

$$ \exists \ C > 0: \ \forall n\in\mathbb\rightarrow\left|x_n\right|\leq C\label $$

Геометрически ограниченность последовательности означает, что все члены последовательности содержатся в С-окрестности точки нуль.

Если последовательность имеет предел, то она ограничена.

В силу теоремы 2 всякая сходящаяся последовательность является ограниченной. Обратное неверно: не всякая ограниченная последовательность является сходящейся. Например, последовательность \(\left\<\left(-1\right)^n\right\>\) ограничена, но не является сходящейся.

Доказать, что последовательность \(\left\<<\textstyle\frac1>\right\>\) является ограниченной, если \(\undersety_n=b, \ b\neq0, \ y_n\neq0 \ для \ всех \ n\in\mathbb\).

Теорема о трех последовательностях или теорема о пределе «зажатой» последовательности.

Если последовательности \(\, \ \, \ \\) таковы, что

$$x_n\leq y_n\leq z_n \ для \ всех \ n\geq N_0,\label$$

то последовательность \(\\) сходится и \(\undersety_n=a\).

По определению предела для любого \(\varepsilon > 0\) найдутся номера \(N_1=N_1(\varepsilon) \ и \ N_2=N_2(\varepsilon)\) такие, что \(x_n\in U_\varepsilon(a)\) при всех \(n\geq N_1\) и \(z_n\in U_\varepsilon(a)\) при всех \(n\geq N_2\).

Рис. 4.3

Отсюда и из условия \eqref следует, что при всех n ≥ N, где N = max(N₀, N₁, N₂), выполняется условие \(y_n\in U_\varepsilon(a)\). Это означает, что существует \(\undersety_n=a\).

\(\triangle\,\)Заметим, что \(\sqrt[n]n-1=\alpha_n > 0\), при \(n > 1\), откуда \(n=(1+\alpha_n)^n > C_n^2\alpha_n^2,\) где\(\displaystyle C_n^2=\frac2 > \frac4,\) при \(n > 2\). Следовательно, \(\displaystyle n > \frac4\alpha_n^2,\) или \(\displaystyle \alpha_n^2 0\), то \(\displaystyle 0 Пример 10.

Если \(a > 1\), то \(a=1+\alpha\), где \(\alpha > 0\), откуда \(a^n=\displaystyle \left(1+\alpha\right)^n > C_n^\alpha^\), при \(n > p\).

Пусть \(n > 2p\), тогда \(\displaystyle C_n^=\frac <(p+1)!>> \frac n<(p+1)!>\left(\frac n2\right)^p\), так как \(\displaystyle n-k > \frac n2\) при \(\displaystyle 1\leq k\leq p\). Отсюда следует, что \(\displaystyle 0 Теорема 4.

Если \(\displaystyle \lim_x_=a\) и a Следствие 2.

\(\circ\) Предположим, что неравенство \eqref не выполняется. Тогда \(a Замечание 3.

В частности, если для сходящейся последовательности \(\\>\) выполняется для всех \(n\in\mathbb\) (или для всех \(n\geq N_0)\) неравенство \(x_\geq \alpha\quad(x_ \leq\beta)\), то \(\displaystyle \lim_x_\geq \alpha\quad(\lim_ x_n\leq\beta)\). Отсюда следует, что если все члены сходящейся последовательности \(\\) принадлежат отрезку \([a,b]\), то есть \(a\leq x_n\leq b\) для всех \(n\in\mathbb\), то и предел этой последовательности принадлежит отрезку \([a,b]\), то есть \(\displaystyle a\leq\lim_x_\leq b\).

В следствии 2 утверждается, что если соответствующие члены двух сходящихся последовательностей связаны знаком нестрогого неравенства, то такое же неравенство справедливо и для пределов этих последовательностей. Короче: предельный переход сохраняет знак нестрогого неравенства. Однако знак строгого неравенства, вообще говоря, не сохраняется, то есть если \(x_n > у_n\) при \(n\geq N_0\) и последовательности \(\\>, \ \\>\) сходятся, то \(\displaystyle <\lim_x_\geq\lim_y_>\). Например, если \(x_=1+\displaystyle \frac<1>, \ y_=1-\displaystyle \frac<1>\), то \(x_n > y_, \ n\in\mathbb\quad\), но \(\displaystyle \lim_x_=\lim_y_=1\).

Источник

Как вычислить предел последовательности?

Мы приступаем к изучению нового раздела математики, который обычно называют «Математический анализ». Он начинается с темы «Производная», которая является основой для изучения дальнейших тем раздела.

Последовательность- это занумерованный ряд объектов. Можно строить последовательности чисел, функций, векторов, рассматривать последовательности событий, утверждений и т.п.

Понятие предела. Предел последовательность. Вычисление пределов

Понятие числовой последовательности.

Тогда говорят, что задана числовая последовательность, и пишут а1, а2,…,аn или (аn), где а1, а2,…,аn – члены последовательности.

Способы задания числовой последовательности.

Другим важным способом задания последовательности является рекуррентный способ, при котором задается выражение, связывающее n-й член последовательности с одним или несколькими предыдущими.

Слово рекуррентный происходит от латинского слова recurrens, что означает «возврат». Вычисляя новый, очередной член последовательности, мы как бы возвращаемся назад и используем уже вычисленные предыдущие члены.

Так же последовательность может быть задана словесным описанием, в котором определяется процесс построения членов последовательности.

Свойства числовой последовательности.

Числовые последовательности могут обладать свойствами, которые мы рассматривали при изучении обычных функций.

Числовая последовательность называется возрастающей, если каждый ее член больше предыдущего, иными словами, если для всякого верно неравенство.

Последовательность называется монотонной, если она является либо возрастающей, либо убывающей.

Последовательность а1, а2,…,аn .. называется ограниченной, если для ее членов можно указать общую границу, т.е. если существует такое число С, что неравенство выполняется для всех номеров n.

Иными словами, последовательность (yn) ограничена сверху, если существует число М такое, что для любого n выполняется неравенство уnМ. Число М называют верхней границей последовательности.

Последовательность (уn) ограничена снизу, если существует число m такое, что для любого n выполняется неравенство уп. Число m называют нижней границей последовательности.

Например, последовательность 1, 4, 9, 16, …, п2, … ограничена снизу. В качестве нижней границы можно взять число 1 или любое число меньше 1.

Понятие предела последовательности.

Рассмотрим две числовые последовательности (уп) и (хп).

(уn):1,3, 5,7,9, …,2n-1,…; (xn):

Изобразим члены этих последовательностей точками на координатной прямой (рис. 1 для (уп) и рис. 2 для (хп)).

Замечаем, что члены второй последовательности (хn) как бы « сгущаются» около точки 0, а у первой последовательности (уп) такой «точки сгущения» нет.

В подобных случаях математики говорят так: последовательность (хn) сходится, а последовательность (уп) расходится.

Возникает естественный вопрос: как узнать, является ли конкретная точка, взятая на прямой, «точкой сгущения» для членов заданной последовательности. Чтобы ответить на данный вопрос, введем новый математический термин.

Опр 1. Пусть а — точка прямой, а r— положительное число. Интервал (а-r, а +r) называют окрестностью точки а (рис. 3), а число r— радиусом окрестности.

Какова окрестность точки 6, если радиус этой окрестности равен 0,02? Ответ: (5,98; 6,02), так как 6-0,02˂ 6 ˂ 6+0,02

Теперь мы можем ответить на поставленный выше вопрос. Но термин «точка сгущения для членов заданной последовательности» обычно заменяют термином «предел последовательности».

Опр 2. Число b называется пределом последовательности (yn), если в любой заранее выбранной окрестности точки b содержатся все члены последовательности, начиная с некоторого номера.

Пишут: уп b (читают: уп стремится к b или уп сходится к b) (читают: предел последовательности уп при стремлении п к бесконечности равен b; но обычно слова «при стремлении п к бесконечности» опускают).

Вычисление предела последовательности.

Рассмотрим предел последовательности, когда х стремится к предельному значению. Простейшим способом вычисления предела является подстановка предельного значения (конкретного числа) в подпредельное выражение, т.е. подставляем число 4 вместо х.

Определение конечного предела последовательности

Приводится определение конечного предела последовательности. Рассмотрены связанные с этим свойства и эквивалентное определение. Приводится определение, что точка a не является пределом последовательности. Рассмотрены примеры, в которых доказывается существование предела, используя определение.

Здесь мы рассмотрим определение конечного предела последовательности. Случай последовательности, сходящейся к бесконечности, рассмотрен на странице «Определение бесконечно большой последовательности».

Определение предела последовательности

Предел последовательности – это такое число a, если для любого положительного числа ε > 0 существует такое натуральное число Nε, зависящее от ε, что для всех натуральных n > Nε выполняется неравенство |xn – a| Читайте также: Какие свойства элементарных функций?

Определение, что число a не является пределом

Утверждение, что число a не является пределом последовательности, означает, что можно выбрать такую ε — окрестность точки a, за пределами которой будет находиться бесконечное число элементов последовательности.

Рассмотрим пример. Пусть задана последовательность с общим элементом. Любая окрестность точки содержит бесконечное число элементов. Однако эта точка не является пределом последовательности, поскольку и любая окрестность точки также содержит бесконечное число элементов. Возьмем ε — окрестность точки с ε = 1. Это будет интервал ( –1, +1).

Все элементы, кроме первого, с четными n принадлежат этому интервалу. Но все элементы с нечетными n находятся за пределами этого интервала, поскольку они удовлетворяют неравенству xn > 2. Поскольку число нечетных элементов бесконечно, то за пределами выбранной окрестности будет находиться бесконечное число элементов. Поэтому точка не является пределом последовательности.

Также можно показать, что любая точка a не может являться пределом этой последовательности. Мы всегда можем выбрать такую ε — окрестность точки a, которая не содержит либо точку 0, либо точку 2. И тогда за пределами выбранной окрестности будет находиться бесконечное число элементов последовательности.

Эквивалентное определение предела последовательности

Можно дать эквивалентное определение предела последовательности, если расширить понятие ε — окрестности. Мы получим равносильное определение, если в нем, вместо ε — окрестности, будет фигурировать любая окрестность точки a.

Предел последовательности – это такое число a, если для любой его окрестности существует такое натуральное число N, так что все элементы последовательности с номерами принадлежат этой окрестности. Это определение можно представить и в развернутом виде.

Предел последовательности

Вначале введем определения числовой последовательности и основные понятия, связанные с числовыми последовательностями.

Для понятия числовой последовательности существуют понятия монотонности и ограниченности.

Предел числовой последовательности

Приведем вначале несколько определений предела числовой последовательности.

С понятием предела числовой последовательности связано понятие сходимости и расходимости числовой последовательности.

Свойства предела числовой последовательности

Теоремы, связанные с понятием предела числовой последовательности

Теорема Вейерштрасса

Пусть числовая последовательность (x_n) монотонно возрастает (убывает), тогда:

Теорема Больцано-Вейерштрасса

Из всякой ограниченной числовой последовательности left(x_n ight) можно извлечь по крайней мере одну подпоследовательность, которая имеет конечный предел.

Теорема — Критерий Больцано-Коши

Для того чтобы числовая последовательность (x_n) имела конечный предел, необходимо и достаточно, чтобы для любого varepsilon >0 существовал номер N, зависящий от varepsilon, такой, что для любых номеров n, m >N выполняется равенство left|x_n-x_m ight|

Примеры задач на вычисление пределов числовой последовательности

Рассматривая далее задачи, мы введем универсальные правила для вычисления некоторых числовых последовательностей.

Пример 1. Найти предел числовой последовательности _ frac<3n^4+2n-1> <4n^3+5n^2-8>>

Пример 2. Найти предел числовой последовательности _ frac <7n^7+5n^2+3>>

Правило 2: Если у числовой последовательности, записанной в виде дроби, степень числителя меньше степени знаменателя, то данный предел равен 0.

Пример 3. Найти предел числовой последовательности _ frac<2n^3-2n+4> <4n^3+8n^2-3>>

Правило: Если у числовой последовательности, записанной в виде дроби, степень числителя равна степени знаменателя, то данный предел равен отношению коэффициентов, стоящих при старших степенях.

Источник

Число e – его смысл и доказательство сходимости последовательности

Определение числа e

Этот предел является частным случаем второго замечательного предела. Число e иногда называют числом Эйлера или числом Непера. Это самое используемое число в математическом анализе. Оно примерно равно
.
Число e можно представить в виде ряда:
.

Далее приводится объяснение, почему оно так популярно в математике, и дается доказательство существования конечного предела (1).

Смысл числа e

Таким образом, смысл применения числа e заключается в том, что через него выражается производная показательной функции, и без него просто нельзя обойтись.

Доказательство сходимости последовательности

Здесь мы покажем, что последовательность с общим членом
(2)
имеет конечный предел. Для этого мы применим теорему Вейерштрасса о пределе монотонной последовательности. Тогда нам нужно доказать, что
1) последовательность (2) монотонна;
2) последовательность (2) ограничена.

Доказательство можно выполнять различными способами.

Применение бинома Ньютона

Отсюда получаем ограниченность :
.

Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.

Применение неравенства Бернулли

Итак, мы показали, что последовательность монотонна и ограничена. Тогда по теореме Вейерштрасса, она имеет конечный предел.

Использование вспомогательной последовательности

Для исследования сходимости исходной последовательности, иногда бывает удобно взять вспомогательную последовательность, которую легче исследовать. При этом предел исходной последовательности должен выражаться через предел вспомогательной.

Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.

Элементы исходной последовательности выражаются через :
.
Далее замечаем, что
.
Применяем теорему о пределе частного числовой последовательности:
.
Поскольку последовательность имеет конечный предел, то и исходная последовательность имеет конечный предел.

Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник