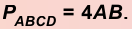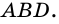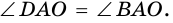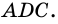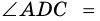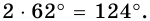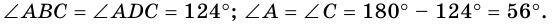Доказать что диагонали ромба взаимно перпендикулярны

Инструменты пользователя

Инструменты сайта

Боковая панель

Геометрия:

Контакты

Ромбом называется параллелограмм, все стороны которого равны (рис.1).

Ромб обладает всеми свойствами параллелограмма.

Рассмотрим особое свойство ромба.

Теорема 1. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

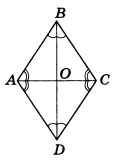
Доказательство. Рассмотрим ромб ABCD (рис.2).

Требуется доказать, что АС ⊥ BD и каждая диагональ делит соответствующие углы ромба пополам. Докажем, например, что ∠ ВАС = ∠ DAC.

По определению ромба АВ = AD, поэтому треугольник BAD равнобедренный. Так как ромб — параллелограмм, то его диагонали точкой О делятся пополам. Следовательно, АО — медиана равнобедренного треугольника BAD, а значит, высота и биссектриса этого треугольника. Поэтому АС ⊥ BD и ∠ ВАС = ∠ DAC, что и требовалось доказать.

Пример 1. Определить углы ромба ABCD (рис.3) при условии, что его меньшая диагональ АС равна стороне ромба.

Решение. Так как по условию диагональ АС равна стороне ромба (а в ромбе все стороны равны), то треугольник ABC — равносторонний и, значит, ∠ ABC = 60°. Тогда (теорема 1) ∠ BAD = 120°. Наконец, по той же теореме ∠ D = ∠ B = 60° и ∠ BCD = ∠ BAD = 120°.

Пример 2. Сторона ромба составляет с его диагоналями два угла, из которых один больше другого на 50%. Вычислить углы ромба.

Решение. Пусть условию задачи удовлетворяет рисунок 2.

Пример 3. Укажите номера верных утверждений.

Источник

Ромб и квадрат

Ромбом называется параллелограмм, у которого все стороны равны.

Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма. Наряду с ними ромб обладает особым свойством. Рассмотрим его.

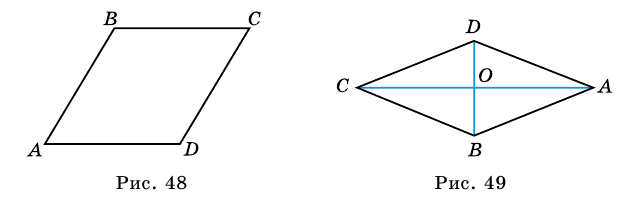
Рассмотрим ромб ABCD (рис. 169). Требуется доказать, что его диагонали АС и BD взаимно перпендикулярны и каждая диагональ делит соответствующие углы ромба пополам. Докажем, например, что ∠ВАС = ∠DAC.

По определению ромба все его стороны равны, в частности АВ = AD, поэтому треугольник BAD равнобедренный. Так как ромб является параллелограммом, то его диагонали точкой О пересечения делятся пополам. Следовательно, отрезок АО — медиана равнобедренного треугольника BAD, проведённая к основанию, а значит, высота и биссектриса этого треугольника. Поэтому AC ⊥ BD и ∠BAC = ∠DAC, что и требовалось доказать.

Квадратом называется прямоугольник, у которого все стороны равны.

Прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т. е. ромбом. Отсюда следует, что квадрат обладает всеми свойствами прямоугольника и ромба. Сформулируем основные свойства квадрата.

Источник

Диагонали ромба

Поскольку ромб является одним из видов параллелограмма, то диагонали ромба в точке пересечения делятся пополам.

Кроме этого, диагонали ромба обладают другими свойствами.

(Свойство диагоналей ромба)

Диагонали ромба пересекаются под прямым углом.

Диагонали ромба являются биссектрисами его углов.

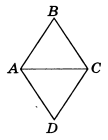
AC и BD — диагонали.

AC и BD — биссектрисы углов ромба.

Рассмотрим треугольник ABC.

Следовательно, треугольник ABC — равнобедренный с основанием AC (по определению равнобедренного треугольника).

Так как диагонали ромба в точке пересечения делятся пополам, то AO=OC.

Значит, BO — медиана треугольника ABC (по определению медианы).

Следовательно, BO — высота и биссектриса треугольника ABC (по свойству равнобедренного треугольника).

BD — биссектриса углов ABC (и ADC).

Из треугольника ABD аналогично доказывается, что AC — биссектриса углов BAD и BCD.

Что и требовалось доказать.

2 Comments

А оно надо так стараться?
Все маленькие треугольники равны по трем сторонам, следовательно углы посередине равны, получаем
4x = 360
x = 90
И про биссектрисы теорема сразу следует из равенства углов

Justifier, стараться надо всегда) Ваше доказательство вполне рабочее. Только надо каждый шаг обосновать. По длине окажется не короче приведенного выше. Геометрия тем и хороша, что доказать утверждение можно разными способами. Доказали по-своему — отлично!

Источник

Ромб и его свойства, определение и примеры с решением

Ромбом называют параллелограмм, у которого все стороны равны (рис. 48).

Так как ромб является параллелограммом, то он имеет все свойства параллелограмма.

1. Сумма любых двух соседних углов ромба равна 180°.

2. У ромба противолежащие углы равны.

3. Диагонали ромба точкой пересечения делятся пополам.

4. Периметр ромба

Кроме того, ромб имеет еще и такое свойство.

5. Диагонали ромба взаимно перпендикулярны и делят его углы пополам.

Доказательство:

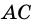
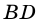
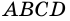
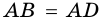
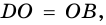
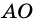
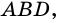
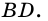
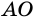
Пусть и — диагонали ромба (рис. 49), — точка их пересечения. Поскольку и то — медиана равнобедренного треугольника проведенная к основанию Поэтому является также высотой и биссектрисой треугольника

Следовательно, 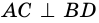и

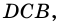
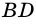
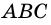
Аналогично можно доказать, что диагональ АС делит пополам угол а диагональ делит пополам углы и

Пример:

Угол между высотой и диагональю ромба проведенными из одной вершины, равен 28°. Найдите углы ромба.

Решение:

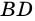
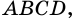
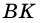
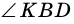
Пусть — диагональ ромба а — его высота (рис. 50), = 28°.

1) В

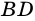
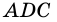
2) Так как делит угол пополам, то

3) Тогда

Ответ. 124°, 56°, 124°, 56°.

Рассмотрим признаки ромба.

Теорема (признаки ромба). Если в параллелограмме: 1) две соседние стороны равны, или 2) диагонали пересекаются под прямым углом, или 3) диагональ делит пополам углы параллелограмма, — то параллелограмм является ромбом.

Доказательство:

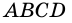
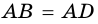
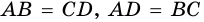
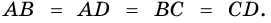
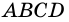
1) Пусть — параллелограмм (рис. 48). Так как (по условию) и (по свойству параллелограмма), то Следовательно, — ромб.

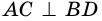
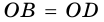
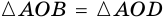
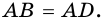
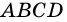
2) Пусть (рис. 49). Поскольку (по свойству параллелограмма), то (по двум катетам). Следовательно, По п. 1 этой теоремы — ромб.

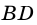
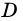
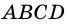
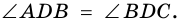
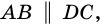
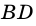
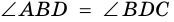
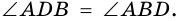
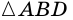
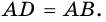
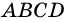
3) Диагональ делит пополам угол параллелограмма (рис. 49), то есть Так как — секущая, то (как внутренние накрест лежащие). Следовательно, Поэтому по признаку равнобедренного треугольника — равнобедренный и По п. 1 этой теоремы — ромб.

Пример:

Доказательство:

Пусть 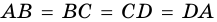(рис. 48).

1) Так как противолежащие стороны четырехугольника попарно равны, то — параллелограмм по признаку параллелограмма.

2) У параллелограмма соседние стороны равны. Поэтому — ромб (по признаку ромба).

Слово «ромб» греческого происхождения, которое в древние времена означало вращающееся тело, веретено, волчок. Ромб тогда связывали с сечением веретена, на которое намотаны нити.

В «Началах» Евклида термин «ромб» встречается единожды, а свойства ромба Евклид вообще не рассматривал.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Свойства диагоналей ромба — основные формулы и доказательство теоремы

При решении математических и физических задач необходимо уметь правильно находить некоторые параметры ромба. Свойства диагоналей могут уменьшить количество и время вычислений. Однако в интернете информация не систематизирована. Кроме того, некоторые сайты наполняются ошибочными данными, которые и путают новичков. Специалисты предлагают специальный алгоритм, помогающий в решении. Однако для этого следует ознакомиться с теорией.

Общие сведения

На начальных этапах при расчетах следует правильно опознать фигуру. Для каждого геометрического тела существуют основные признаки, по которым она идентифицируется. Кроме того, некоторые параметры взаимосвязаны между собой некоторыми зависимостями. У каждой из них есть такие характеристики: размер сторон, углы, периметр, площадь, а также свойства, полученные при доказательстве теорем.

В любой дисциплине с физико-математическим уклоном существуют аксиомы и теоремы. Первые не требуют доказательства, а для вторых — оно необходимо. Последние доказываются на основании аксиом или доказательств других теорем. При изучении какой-либо фигуры следует начинать с определения, исходя из которого можно получит некоторую важную информацию.

Информация о ромбе

Ромбом называется параллелограмм, который имеет равные стороны. Частным его случаем считается квадрат, у которого внутренние углы при вершинах прямые. Фигуры отличаются размером сторон и углами. Однако для всего типа действуют признаки и свойства. Некоторые путают эти два термина. Однако они существенно отличаются между собой.

С помощью признаков можно правильно распознать фигуру, а потом применить необходимые формулы для решения задач. Свойства используются только после идентификации. Они позволяют вычислить некоторые параметры или доказать теоремы. Достаточно двух признаков для точного определения типа фигуры.

Чтобы не запутаться в терминологии математики предлагают простые определения. Признаками является характерные параметры, которые присущи определенному типу геометрического тела. Свойства — совокупность утверждений, которые применяются для нахождения параметров, величин, доказательства тождеств и решения уравнений.

Основные признаки

Ромб имеет такие же признаки, как и параллелограмм. Однако существуют некоторые критерии, по которым можно отличить эти две фигуры:

Однако под эти признаки попадает не только ромб, но и квадрат. Существует специальный алгоритм, позволяющий выяснить принадлежность четырехугольника к той или иной группе. Он состоит из следующих шагов:

Например, у четырехугольника с прямыми внутренними углами диагонали пересекаются в некоторой точке, и образуют 4 треугольника с прямым углом. Следует идентифицировать тип фигуры. Для этого нужно воспользоваться вышеописанным алгоритмом:

Алгоритм является очень простым. При его применении не возникает проблем вообще.

При использовании признаков и алгоритма специалисты-математики гарантируют точность определения. После идентификации фигуры необходимо обратить внимание на ее свойства.

Важные свойства

Ромб обладает всеми свойствами параллелограмма, которые следует учитывать. Ошибка некоторых новичков заключается в том, что они при поиске свойств не обращают внимания на частные случаи. Из-за невнимательности некоторые задачи решаются очень долго, а иногда произвести вычисления просто невозможно. К основным свойствам параллелограмма относятся следующие:

Ромб обладает также свойствами, которые присущи только ему. Это связано с тем, что он является частным случаем класса параллелограммов. К ним необходимо отнести следующие:

Некоторые из свойств были получены при доказательстве теорем. Для выведения третьего свойства использовалась теорема Пифагора.

Теоремы о диагоналях

В геометрии всего две теоремы о диагоналях ромба. Для удобства их можно объединить в одну с такой формулировкой: диагонали ромба взаимно перпендикулярны и являются биссектрисами внутренних углов фигуры. Для доказательства следует рассмотреть сначала первое свойство, которое называется теоремой о свойстве диагоналей ромба.

Для этого необходимо начертить произвольный ромб ABCD с диагоналями, которые будут обозначаться АС = d1 и BD = d2. Они пересекаются в некоторой точке W. По восьмому свойству параллелограмма: AW = CW, т. е. они будут делиться на два равных отрезка (половина длины диагонали).

После этого нужно рассмотреть треугольник ABC, который является равнобедренным по определению ромба, а также по третьему признаку. Если AW = CW, то BW является его медианной. В равнобедренном треугольнике она является биссектрисой, а также высотой. Последняя — проходит под прямым углом к противолежащей стороне. Следовательно, перпендикулярность двух диагоналей доказана.

В треугольнике ABC отрезок BW — биссектриса угла B. Аналогично необходимо доказывать для углов A, С и D (рассматриваются треугольники BAD, BCD и ADC соответственно). Таким методом доказано и второе свойство ромба. Однако для решения задач недостаточно признаков и свойств. Для этих целей необходимо использовать формулы.

Формулы для вычислений

Каждую геометрическую характеристику ромба можно определить, используя некоторые соотношения. В задачах бывают известны определенные значения. Однако их бывает недостаточно, поскольку для вычисления какого-либо параметра следует найти промежуточные величины.

Чтобы правильно понимать формулы, следует ввести некоторые обозначения. Они позволят заметно сократить записи. Этот особый подход часто применяют математики. Пусть дан ромб, который имеет такие параметры:

Кроме того, у него есть такие характеристики, как площадь (размерность) и периметр. Они обозначаются литерами S и P соответственно.

Периметр и размерность

Периметром геометрической фигуры называется величина, которая эквивалентна суммарному значению всех его сторон. Площадь — характеристика геометрического тела, которая показывает его размерность. Следует отметить, что размерность существует только у двумерной фигуры. Если последняя принадлежит трехмерному пространству, то необходимо вычислять ее объем, поскольку размерности у нее нет.

Для определения периметра существует одна формула P = 4a. Однако сторону можно выражать через S, R, D, d1, d2, высоту h, а также через углы f и g. Для S существует больше соотношений. Некоторые из них можно также дополнительно вывести, выражая через некоторые параметры. Базовыми формулами являются следующие:

В последнее соотношение необходимо верно подставлять значения. Нужно обратить внимание на то, что берется произведение большей диагонали d1 на тангенс острого угла g, и наоборот — значение меньшей диагонали, умноженной на тангенс тупого угла g.

Длина стороны

В задачах определенного типа возникает необходимость найти длину стороны. Для нахождения этого параметра ромба существуют также формулы и соотношения, которые помогут получить верный ответ. К базовым из них можно отнести следующие:

Чтобы вычисления были верными, необходимо учитывать, что в 5 и 6 пунктах угол f — острый, a g — тупой. Функция «sqrt» применяется в различных математических пакетах и языках программирования. Она эквивалентна квадратному корню из числа, которое находится под корнем.

Соотношения для диагоналей

Существуют определенные задачи, в которых необходимо найти диагонали ромба. Можно, конечно, не пользоваться готовыми формулами, а выводить их. Математики рекомендуют осуществлять такие операции, поскольку идет тренировка мозга. Однако в некоторых ситуациях, например на контрольной или экзамене, время не хватает. Следовательно, на решение нужно тратить меньше времени.

Как бы быстро ни считал человек в уме или пользовался калькулятором, лишние вычисления занимают много времени. Следовательно, для оптимизации нужно пользоваться готовыми соотношениями, позволяющими находить нестандартные параметры. К ним можно отнести вычисление длины диагоналей ромба (d1 — большая, d2 — меньшая). Для этого следует применять такие формулы:

В 11 и 12 формулах следует обратить особое внимание на обозначения углов. Острый угол — f, а тупой — g. Следует отметить, что все 12 пунктов — базовые формулы для нахождения диагоналей. Однако можно выводить соотношения самостоятельно, как в пунктах 5 и 6 (замена a 2 на S).

Вписанная окружность

Когда в ромб вписана окружность, то появляются другие соотношения. Очень часто математики специально вписывают ее, поскольку в результате такой операции открывается больше возможностей. Базовые соотношения следующие:

Необходимо отметить, что R = D / 2. Если умножить каждое из соотношений на 2, то можно получить значение диаметра D вписанной окружности.

Таким образом, очень важным шагом при решении задачи является идентификация геометрической фигуры. После этого можно применять основные формулы для нахождения неизвестных величин.

Источник