Доказать что диагональные матрицы перестановочны
Являются ли матрицы перестановочными
Вариант №3
Задание № 1. Алгебра матриц
2) Произведение матриц АВ и ВА. Выяснить, является ли данные матрицы перестановочными.
Решение.
1) Найдем 2А:
Найдем 3B:
Вычисляем 2А-3В: 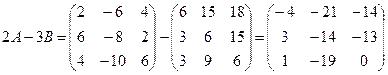
2)
Так как АВ≠BA, то матрицы А и В не являются перестановочными.
Задание № 2. Определители
Вычислить определитель пятого порядка:
Решение.
Запишем матрицу в виде:
Преобразуем 1-ый столбец таким образом, чтобы в нем оказалось максимальное количество нулей.
Полученную матрицу разложим по элементам 1-ого столбца и преобразуем ее:
Добавим 4-ую строку к 3-ой:
| C 3 +C 4 = | 11 /4 | 3 /4 | 3 /4 | 3 /4 |
| -2 | ||||
| -2 | ||||
| -1 |
Добавим 3-ую строку к 4-ой:
| C 4 +C 3 = | 11 /4 | 3 /4 | 3 /4 | 3 /4 |
| -2 | ||||
| -2 | ||||
| -2 | -1 |
Умножим 1-ую строку на (k = 2 / 11 /4 = 8 /11) и добавим к 2-ой:
| C 2 + 8 /11C 1 = | 11 /4 | 3 /4 | 3 /4 | 3 /4 |
| 28 /11 | 6 /11 | 6 /11 | ||
| -2 | ||||
| -2 | -1 |
Полученную матрицу разложим по элементам первого столбца и преобразуем ее:
Умножим 1-ую строку на (k = 2 / 28 /11 = 11 /14) и добавим к 2-ой:
| C 2 + 11 /14C 1 = | 28 /11 | 6 /11 | 6 /11 |
| 3 /7 | 17 /7 | ||
| -1 |
Полученную матрицу разложим по элементам первого столбца и преобразуем ее:
Определитель равен ∆ = 4 * 11 /4 * 28 /11 * ( 3 /7*2 – (-1)* 17 /7) = 92
Ответ:
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9530 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Доказать, что для того чтобы квадратная матрица А была перестановочна со всеми квадратными матрицами того же порядка, необходимо и достаточно, чтобы матрица А была скалярной.
Пусть порядок А равен n и для любой квадратной матрицы B порядка n выполнено AB = BA.
Рассмотрим в качестве матрицы B матрицу, у которой все элементы равны нулю, кроме i-го диагонального. Пусть он равен d.
Тогда в AB все стобцы будут нулевые, кроме i-го, который будет равен i-му столбцу матрицы A, умноженному на d.
Перебирая все i от 1 до n, получаем, что матрица A необходимо должна быть диагональной. Теперь докажем что она должна быть скалярной.
Рассмотрим в качестве матрицы B матрицу элементарного преобразования, которое меняет местами 1-ый и i-ый столбцы.
Рассматриваются матрицы, результатом умножения которых на любую прямоугольную матрицу является перестановка ее строк или столбцов.
Непосредственным вычислением легко проверяются следующие свойства матрицы перестановок.
Таким образом, если в i-ой строке матрицы перестановок P единица расположена в j-ом столбце, то умножение матрицы P слева на матрицу A приводит к перемещению j-ой строки матрицы A в позицию i-ой строки.
Аналогично, если в i-ом столбце матрицы перестановок P единица расположена в j-ой строке, то умножение матрицы P справа на матрицу A приводит к перемещению j-го столбца матрицы A в позицию i-го столбца.
Если матрицы перестановок P получена из единичной матрицы E перестановкой местами двуз строк (или двух столбцов), то такая матрица называется элементарной матрицей перестановок.
При умножение слева элементарной матрицы перестановок на матрицу A происходит перестановка соответствующих строк матрицы A.
Умножение справа элементарной матрицы перестановок на матрицу A приводит к перестановке соответствующих столбцов матрицы A.
Для любой матрицы перестановок P справедливы следующие свойства:
где 
где 
Терема 1. Произведение матриц перестановок одного и того же порядка есть матрица перестановок.
Терема 2. Матрица перестановок n-го порядка может быть представлена в виде произведения (n – 1) элементарных матриц перестановок.
Терема 3. Квадрат элементарной матрицы перестановок есть единичная матрица.
Доказать утверждение
В формулировке утверждения присутствуют слова «необходимо и достаточно».
Это означает, что Ваше доказательство должно состоять из двух частей:
Часть первая. НЕОБХОДИМОСТЬ.
Вы должны привести пример двух матриц A и D таких, что D — диагональная,
A — не диагональная, и матрицы A и D не перестановочны (AD не равно DA).
Часть вторая. ДОСТАТОЧНОСТЬ.
Здесь уже примерами не обойтись. Требуется рассуждение.
Нужно доказать, что ЛЮБЫЕ диагональные матрицы A и D перестановочны (AD=DA).
Небольшое уточнение.
В #4 я предполагаю, что мы заранее зафиксировали размер матриц, например, 3×3.
И это же как бы подразумевается и в старт-посте.
Но строго говоря, утверждение старт-поста должно формулироваться так:
Пусть n — произвольное натуральное число.
Для того, чтобы квадратная матрица А размера n x n была перестановочна
со всеми диагональными матрицами размера n x n, необходимо и достаточно,
чтобы матрица А сама была диагональна.
Если мы зафиксировали n, например, n=3, то в ПЕРВОЙ ЧАСТИ доказательства
(НЕОБХОДИМОСТЬ) можно привести один какой-нибудь пример двух матриц A и D
размера 3×3 таких, что D — диагональная, A — не диагональная,
и матрицы A и D не перестановочны (AD не равно DA).
Но если мы не зафиксировали n, то одного примера не достаточно.
Необходимо некоторое рассуждение, показывающее, что при любом n
такой пример существует.
Вы не понимаете, что такое НЕОБХОДИМОСТЬ.
Пока был пост №4 — я думал, что Вы описались, и не стал комментировать. Но потом появился пост №7, дублирующий Ваши грубейшие заблуждения.
То, что Вы предлагаете, НЕОБХОДИМОСТЬ не доказывает даже близко.
Доказать утверждение о вещественной треугольной матрице

Как привести матрицу к унитреульной матрице или верхней треугольной матрице? Добавлено через 14.
Доказать утверждение
Объясните, как доказать или опровергнуть утверждение о произвольных множествах A, B, C методом.
Доказать утверждение
Подскажите, как быть с такими гипотезами, что то торможу, как аксиомы применить к такому, похоже.
Доказать утверждение
Доказать,что пересечение двух подгрупп А и В группы G будет подгруппой конечного индекса в группе.
Нет: a11^2 + a12^2 + a13^2; a22^2 + a23^2; a33^2.
Решение
Значит, матрицы A еще нет (то есть она не дана), и ее существование нужно доказать.
Диагонализируемость в данном случае не нужна, да ее и нет, как правило.
Треугольная матрица Х вычисляется из уравнения X 2 =C для треугольной же матрицы С с положительной диагональю так. Вначале вычисляем диагональные элементы из уравнений
» />
Затем, зная диагональные элементы Х и учитывая положительность диагональных элементов С, вычисляем элементы, стоящие на диагонали, параллельной главной, из формулы
» />
После этого переходим к следующей диагонали и т.д.
Рекомендую проделать все выкладки для матриц порядков 2, 3, 4. Все станет ясно.
Доказать утверждение
Докажите, что любое счетное линейно упорядоченное множество изоморфно некоторому подмножеству.
Доказать утверждение
Помогите доказать, пожалуйста:help:
Доказать утверждение
Здравствуйте. Как доказать следующее утверждение: Изоморфные графы имеют одинаковые хроматические.
Доказать утверждение
Подскажите пожалуйста как доказываются такого рода утверждения: A\subseteq B тогда и только тогда.
Доказать что диагональные матрицы перестановочны
Виктор Цекунов
Навигация
Affiliations
Template tips
2. Алгебра
___________________________________________________________________________
Оказываю платные услуги: решение задач по высшей математике. Оплата WebMoney.
Заказы направляйте сюда: Платные услуги
___________________________________________________________________________
2.1. Арифметика целых чисел.
2.2. Матрицы и определители.
2.3. Системы линейных уравнений.
2.4. Множества и отображения.
2.5. Комплексные числа.
2.8. Алгебраические уравнения.
2.9. Элементы теории полей.
2.10. Линейные пространства.
2.11. Линейные операторы.
2.12. Квадратичные формы.
2.1. Арифметика целых чисел.
2.1-1. Используя алгоритм Евклида сократить дробь: 169/448.
Решение:
Применяя алгоритм Евклида, получаем равенства (в правой части равенств после плюса стоят остатки):
448 = 169∙2 + 110,
169 = 110∙1 + 59,
110 = 59∙1 + 51,
59 = 51∙1 + 8,
51 = 8∙6 + 3,
8 = 3∙2 + 2,
3 = 2∙1 + 1,
2 = 1∙2.
Так как последний отличный от нуля остаток равен 1, то наибольший общий делитель чисел 448 и 169
НОД(448, 169) = 1.
Это означает, что числа 448 и 169 – взаимно простые. Следовательно, дробь
169/448 несократима.
2.1-2. Используя алгоритм Евклида сократить дроби: 490/1372; 92400/13960
Решение:
1) Д робь 490/1372:
Применяя алгоритм Евклида, получаем равенства (в правой части равенств после плюса стоят остатки):
1372 = 490∙2 + 392,
490 = 392∙1 + 98,
392 = 98∙4.
Так как последний отличный от нуля остаток равен 98, то наибольший общий делитель чисел 1372 и 490
НОД(1372, 490) = 98.
Сокращаем дробь на 98
(490:98)/(1372:98) = 5/14.
Вычислим M ₁.
M ₁ = 30636⁻¹ mod 13 или
30636 M ₁ mod 13=1,
30636 mod 13 · M ₁ mod 13=1,
8 · M ₁ mod 13=1, отсюда
8 M ₁ может принимать значения 14, 27, 40, …
Т.к. 40 делится на 8, то из уравнения
8 M ₁ = 40 находим
M ₁=40/8=5.
Вычислим M ₃.
M ₃ = 17316⁻¹ mod 23 или
17316 M ₃ mod 23=1,
17316 mod 23 · M ₃ mod 23=1,
20 · M ₃ mod 23=1, отсюда
20 M ₃ может принимать значения 24, 47, 70, 93, 116, 139, 162, 185, 208, 231,
254, 277, 300, …
Т.к. 300 делится на 20, то из уравнения
20 M ₃ = 300 находим
M ₃=300/20=15.
Вычислим M ₄.
M ₄ = 11063⁻¹ mod 36 или
11063 M ₄ mod 36=1,
11063 mod 36 · M ₄ mod 36=1,
11 · M ₄ mod 36=1, отсюда
11 M ₄ может принимать значения 37, 73, 109, 145, 181, 217, 253, …
Т.к. 253 делится на 11, то из уравнения
11 M ₄ = 253 находим
M ₄=253/11=23.
Подставим всё в (1)
x = (6 · 30636 · 5 + 33 · 10764 · 12 + 19 · 17316 · 15 + 14 · 11063 · 23) mod398268 =
= 13678970 mod398268 = 137858.
Ответ: x = 137858.
________________________________________________________________________________________________
2.2. Матрицы и определители.
2.2-2. Найдите все матрицы, перестановочные с матрицей
Решение:
Пусть матрица %20%D0%9C%D0%90%D0%A2.jpg)
АВ = ВА. (1)
Вычислим произведения матриц: АВ и ВА.
Итак, мы получили
det ( λA ) = λ ⁿ· detA и формула (1) доказана!
2. Из формулы (1) при n = 4, det A = 3 получаем
det 3 A = 3⁴· det A = 3⁴·3 = 3⁵= 243.
Ответ: det 3A = 3⁴·det A = 243.
2.3. Системы линейных уравнений.
2.3-2. Дана система уравнений:
Как выглядит базисное решение этой системы?
( к 2-й строке +3-ю строку, умноженную на (-2) )
( поменяем местами 2-ю и 3-ю строки )
2.3-4. Проверить, является ли система линейных уравнений
невырожденной, и решить её по формулам Крамера.
Решение:
1. Матрица А данной системы:
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =
= (разложим определитель по 1-му столбцу) =
= (к 3-й строке прибавим 2-ю строку, умноженную на 3) =
= (разложим определитель по 1-му столбцу) =
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =
= (разложим определитель по 1-му столбцу) =
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =
= (разложим определитель по 1-му столбцу) =
2.5. Комплексные числа.
2.11. Линейные операторы.
Разложим определитель по 1-му столбцу
2.12. Квадратичные формы.
2.12-1. Как определить являются ли линейными преобразования каких-либо выражений?
________________________________________________________________________________________________
2.13. Тензоры.
2.13-1. Вычислить свертку Cijbkj+BmEikm
Описание файла
Просмотр DJVU-файла онлайн
Матрицы 2.9. Показать, что: а) для выполнимости клеточного умножения двух блочных квадратных матриц достаточно, чтобы диагональные клетки были квадратными, причем порядки соответствующих диагональных клеток были равны между собой. Является ли это условие необходимым? б) для выполнимости клеточного умножения блочной матрицы на себя необходимо и достаточно, чтобы все ее диагональные клетки были квадратными. 2.10. Доказать, что множество верхних (нижних) квазитреугольных матриц одинакового порядка и одинаковой клеточной структуры замкнуто относительно умножения. 2.11. Пусть А и  — квазидиагональные матрицы одного порядка и одинаковой клеточной структуры. Доказать, что: а) произведение АВ есть квазидиагональная матрица, диагональные клетки которой равны произведениям А,,В„одноименных диагональных клеток сомножителей; б) матрицы А и В перестановочны тогда и только тогда, когда перестановочны их одноименные диагональные клетки.
2.12. Пусть А Е К «» и В Е Кв»»‘ — произвольные матрицы. Доказать тождество АВ О 1 А 1
А О О в котором 1 и 1„— единичные матрицы порядка т и и соответственно, а символом О обозначены нулевые матрицы подходящих размеров. 2.13. Пусть А — произвольная квадратная матрица. Доказать, что симметрическая матрица, перестановочная с матрицей А, перестановочна также с матрицей Ат. Верно ли обратное: если некоторая матрица перестановочна и с А, и с А
, то она обязательно симметрическая? 2.14. Доказать, что квадратная матрица А порядка п кососимметрическая тогда и только тогда, когда соотношение х гАх = 0 выполнено для любого вектор-столбца я е К»»
2.15. Пусть матрицы А и В симметрические. Доказать, что: а) А+ В и оА для любого о е К вЂ” симметрическая матрица; б) А
— симметрическая матрица при любом й е Я, в) матрица АВ является симметрической тогда и только тогда, когда матрицы А и В перестановочны. 25
Матрицы специального вида 2.16. Доказать, что если А и  — симметрические квадратные матрицы одинакового порядка, то матрица С = (АВ)»А является симметрической для любого и Е И. 2.17. Показать, что для любой матрицы А матрица ААт является симметрической. 2.18. Пусть матрицы А и В кососимметрические. Доказать, что: а) А + В и оА для любого о е И вЂ” кососимметрическая матрица; б) А» — кососимметрическая матрица при нечетном й и симметричная матрица при четном а; в) матрица АВ является симметрической тогда и только тогда, когда матрицы А и В перестановочны.
г) Сформулировать и доказать необходимое и достаточное условие кососимметричности произведения АВ. 2.19. Доказать, что произведение симметрической и кососимметрической матриц является кососимметрической матрицей тогда и только тогда, когда эти матрицы перестановочны. 2.20. а) Пусть А — произвольная симметрическая матрица. Доказать, что матрица А+Ат симметрическая, а матрица А — Ат кососимметрическая.
б) Доказать, что любую квадратную матрицу можно разложить в сумму симметрической и кососимметрической матриц. Единственно ли такое разложение? 2.21. Разложить матрицу А в сумму симметрической и косо- симметрической матриц: 1 — 1 2 1 3 — 2; в)А= — 2 2 0 а) А= 3 10 ‘ б) 2 О 2 О 1 — 2 О 0 — 1 2.22. Доказать, что если матрицы А и В обе симметрические или кососимметрические, то а) их коммутатор
А, В] — кососимметрическая матрица, б) их произведение Йордана А* — симметрическая матрица. 2.23. Доказать, что всякая кососимметрическая матрица является коммутатором диагональной и симметрической матрицы. 2.24. а) Пусть А — симметрическая матрица.
Доказать, что величина
г Ат неотрицательна, причем равна нулю тогда и только тогда, когда матрица А нулевая. Глава 1. Матрицы б) Сформулировать и доказать аналогичное утверждение для кососимметрических матриц. 2.25. Пусть А и  — симметрические матрицы одного порядка. Доказать, что выполнено неравенство сг(АВ)з ( 1г(АзВз), которое переходит в равенство тогда и только тогда, когда матрицы А и В перестановочны. 2.26. Доказать, что если симметрическая матрица А нильпотентна с индексом нильпотентности, равным двум, то А — нулевая.
Верно ли данное утверждение для кососимметрической матрицы А? 2.27. Найти: а) все ортогональные матрицы второго порядка; б) все симметрические ортогональные и кососимметрические ортогональные матрицы второго порядка. 2.28. Пусть вектор-столбец т удовлетворяет условию ттх = 1. Доказать, что матрица У = 1 — 2ххт является одновременно симметрической и ортогональной. 2.29. Доказать, что множество ортогональных матриц одного порядка замкнуто относительно операции умножения матриц.
2.30. Показать, что матрица А = (аб) Е К»»» ортогональна тогда и только тогда, когда для ее строк (столбцов) имеет место соотношение в / и Е пьа,ь=д,
аыаь =4 ь=1 ь=1 2.31. Доказать, что вещественная треугольная матрица ортогональна тогда и только тогда, когда она диагональна, причем элементы ее главной диагонали равны 1 или — 1. / А1 2.32. Доказать, что блочная матрица А
, в которой матрица А и единичная матрица 1 — квадратные одного порядка, ортогонвльна в том и только в том случае, когда А = О.
, в которой матрица А и единичная матрица 1 — квадратные одного порядка, нильпотентна в том и только в том случае, когда нильпотентна матрица 1+ Аз.
Найти все периодические матрицы второго порядка с периодом, равным двум. 2.42. Доказать, что произведение двух перестановочных периодических матриц является периодической матрицей. Верно ли это утверждение, если матрицы не перестановочны? 2.43. Доказать, что если А»‘ + А
‘ +. + А + 1 = О для некоторого т е 1Ч, то матрица А периодическая. 1 А1 2.44. Доказать, что блочная матрица 1
, в которой ‘См. также задачи 8.1, 16.56. См. также задачи 9.61, 16.5?. 2. 34. Доказать, что сумма и произведение двух перестановочных нильпотентных матриц является нильпотентной матрицей. Верно ли это утверждение, если матрицы не перестановочны? 2.35.1 Найти все нильпотентные матрицы второго порядка с индексом нильпотентности 2. 2.36. Доказать, что треугольная матрица нильпотентна тогда и только тогда, когда ее главная диагональ нулевая.
2.38. Доказать, что коммутатор треугольных матриц одного вида является нильпотентной матрицей. 2.39. Показать, что квазитреугольная матрица нильпотентна тогда и только тогда, когда нильпотентны все ее клетки на главной клеточной диагонали. Глава 1. Матрицы 28 матрица А и единичная матрица 1 — квадратные одного порядка, периодическая в том и только в том случае, когда матрица 1+А 2 является периодической. 2.45.
Экспонентой матрицы А (по аналогии с экспонентой числа) называют сумму ряда СО ехр А = 1+
— А». И ь=1 (2.1) — 4 — 2, б)А= 2.47. Д оказать, что если А — диагональная матрица, то ехр А также диагональна, причем если А = йа8(оы. а„1, то ехр А = йаб
е ‘. е «1. 0 11 2.48. Доказать, что если А =
, то для любого а Е К ехр(аА) = сова 1+япа А. 2.49.
Доказать, что если А — периодическая матрица с периодом 2, то для любого а е К ехр(оА) = сЬо 1+зло А. 2.50. Доказать, что если матрицы А и В перестановочны, то ехр(А + В) = ехр А ехр В. 2.51. Квадратная матрица А с неотрицательными элементами называется стохастической, если все ее строчные суммы равны 1. Если же при этом еще и каждая столбцовая сумма также равна 1, то матрица называется деамсды сглохастической.
Доказать, что: а) произведение стохастических матриц является стохастической матрицей; Сходимость ряда в (2.1) понимается как сходимость рядов, получающихся при вычислении ках
дого элемента матрицы — суммы ряда в правой части. а) Пользуясь признаком сравнения, доказать абсолютную сходимость ряда (2.1) для любой квадратной матрицы А.
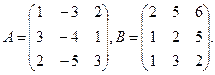
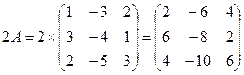
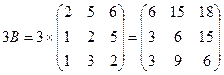
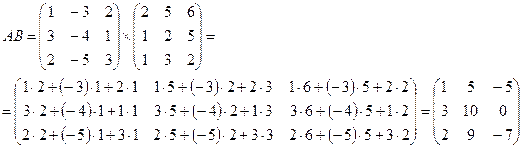
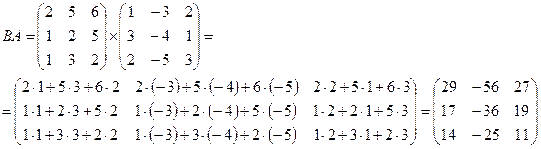
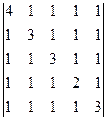
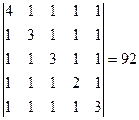




.jpg)
%20%D0%9C%D0%90%D0%A2.jpg)
%20%D0%9C%D0%90%D0%A2.jpg)
%20%D0%9C%D0%90%D0%A2.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
%20%D0%9C%D0%90%D0%A2.jpg)
%20%D0%9C%D0%90%D0%A2.jpg)