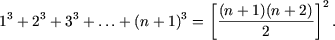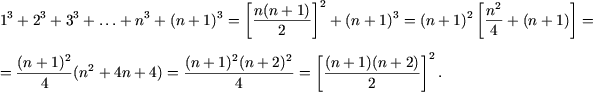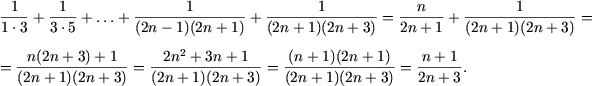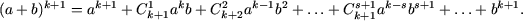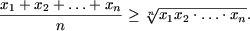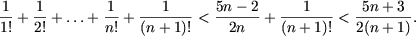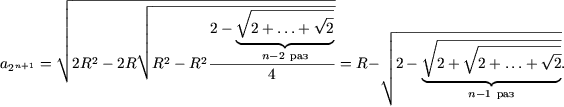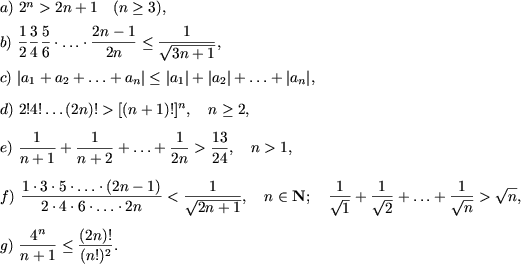Доказать что для любого натурального числа n значение выражения
Доказать что для любого натурального числа n значение выражения
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
т. е. утверждение справедливо и при n + 1.
Пример 1. Доказать следующие равенства
Решение. a) При n = 1 равенство примет вид 
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Используя предположение индукции, получим
Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.
c) При n = 1 равенство истинно: 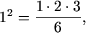
d) При n = 1 равенство справедливо: 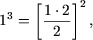
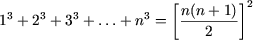
e) Утверждение P(1) справедливо: 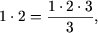
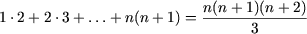
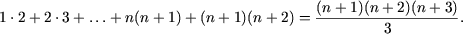
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1) справедливо: 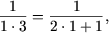
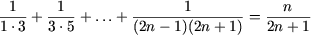
Действительно, учитывая, что P(n) имеет место, получим
Таким образом, равенство доказано.
g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть,
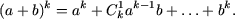
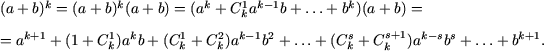
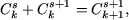
Пример 2. Доказать неравенства
Решение. a) При n = 1 получаем истинное неравенство
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
Рассмотрим следующие два случая:
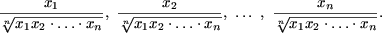
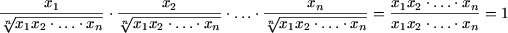
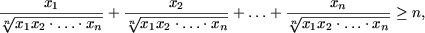
sin 2n a + cos 2n a ≤ 1 и покажем, что имеет место P ( n + 1). Действительно, sin 2(n + 1) a + cos 2(n + 1) a = sin 2n a ·sin 2 a + cos 2n a ·cos 2 a 2n a + cos 2n a ≤ 1 (если sin 2 a ≤ 1, то cos 2 a 2 a ≤ 1, то sin 2 a n О N sin 2n a + cos 2n ≤ 1 и знак равенства достигается лишь при n = 1.
e) При n = 1 утверждение справедливо: 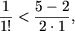
Допустим, что 
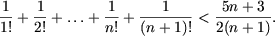
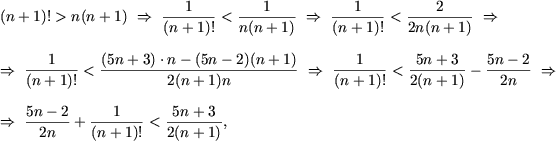
Поскольку при n > 10 имеем 
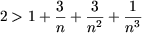
Пример 3. Доказать, что для любого n О N

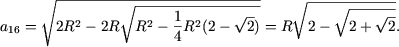
 | (2) |
Как ранее было показано при n = 1, что эта формула справедлива. Пусть (2) выполняется при n = k. Вычислим 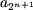
Замечание. Из (2) следует, что длина окружности равна
I. Доказать равенства
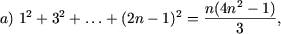 |
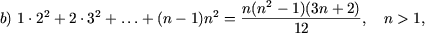 |
 |
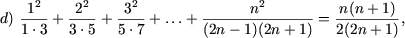 |
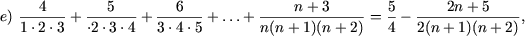 |
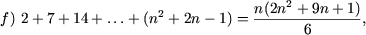 |
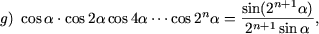 |
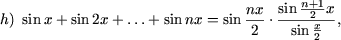 |
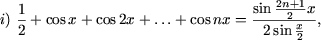 |
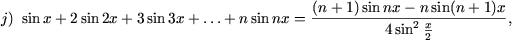 |
 |
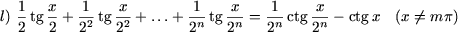 |
 |
II. Доказать неравенства
III. Доказать, что при любом натуральном n число an делится на b
IV. Показать, что 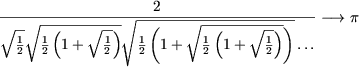
VI. Пусть даны n произвольных квадратов. Доказать, что эти квадраты могут быть разрезаны так, чтобы из получившихся частей можно было образовать квадрат.
Применение метода математической индукции к решению задач на делимость натуральных чисел
Рубрика: Математика: алгебра и начала анализа, геометрия
Дата публикации: 02.05.2015 2015-05-02
Статья просмотрена: 9372 раза
Библиографическое описание:
Баданин, А. С. Применение метода математической индукции к решению задач на делимость натуральных чисел / А. С. Баданин, М. Ю. Сизова. — Текст : непосредственный // Юный ученый. — 2015. — № 2 (2). — С. 84-86. — URL: https://moluch.ru/young/archive/2/128/ (дата обращения: 06.12.2021).
В математических олимпиадах часто встречаются достаточно трудные задачи на доказательство делимости натуральных чисел. Перед школьниками возникает проблема: как найти универсальный математический метод, позволяющий решать подобные задачи?
Оказывается, большинство задач на доказательство делимости можно решать методом математической индукции, но в школьных учебниках уделяется очень мало внимания этому методу, чаще всего приводится краткое теоретическое описание и разбирается несколько задач.
Метод математической индукции мы находим в теории чисел. На заре теории чисел математики открыли многие факты индуктивным путем: Л. Эйлер и К. Гаусс рассматривали подчас тысячи примеров, прежде чем подметить числовую закономерность и поверить в нее. Но одновременно они понимали, сколь обманчивыми могут быть гипотезы, прошедшие «конечную» проверку. Для индуктивного перехода от утверждения, проверенного для конечного подмножества, к аналогичному утверждению для всего бесконечного множества необходимо доказательство. Такой способ предложил Блез Паскаль, который нашел общий алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число (трактат «О характере делимости чисел).
Метод математической индукции используется, чтобы доказать путем рассуждений истинность некоего утверждения для всех натуральных чисел или истинность утверждения начиная с некоторого числа n.
Решение задач на доказательство истинности некоторого утверждения методом математической индукции состоит из четырех этапов (рис. 1):
Рис. 1. Схема решения задачи
1. Базис индукции. Проверяют справедливость утверждения для наименьшего из натуральных чисел, при котором утверждение имеет смысл.
2. Индукционное предположение. Предполагаем, что утверждение верно для некоторого значения k.
3. Индукционный переход. Доказываем, что утверждение справедливо для k+1.
4. Вывод. Если такое доказательство удалось довести до конца, то, на основе принципа математической индукции можно утверждать, что утверждение верно для любого натурального числа n.
Рассмотрим применение метода математической индукции к решению задач на доказательство делимости натуральных чисел.
Пример 1. Доказать, что число 5 
1) Проверим, что эта формула верна при n = 1: число 
2) Пусть эта формула верна для n = k, т. е. число 
3) Докажем, что формула верна и для n = k + 1, т. е.

4) Оба условия принципа математической индукции выполнены, следовательно, предложение истинно при всех значениях n.
Пример 2. Доказать, что сумма кубов трех последовательных натуральных чисел делится на 9.
Докажем утверждение: «Для любого натурального числа n выражение n 3 +(n+1) 3 +(n+2) 3 кратно 9.
1) Проверим, что эта формула верна при n = 1: 13+23+33=1+8+27=36 кратно 9.
2) Пусть эта формула верна для n = k, т. е. k 3 +(k+1) 3 +(k+2) 3 кратно 9.
3) Докажем, что формула верна и для n = k + 1, т. е. (k+1) 3 +(k+2) 3 +(k+3) 3 кратно 9. (k+1) 3 +(k+2) 3 +(k+3) 3 =(k+1) 3 +(k+2) 3 + k 3 + 9k 2 +27 k+ 27=(k 3 +(k+1) 3 +(k+2) 3 )+9(k 2 +3k+ 3).
Полученное выражение содержит два слагаемых, каждое из которых делится на 9, таким образом, сумма делится на 9.
4) Оба условия принципа математической индукции выполнены, следовательно, предложение истинно при всех значениях n.
Пример 3. Доказать, что при любом натуральном n число 3 2n+1 +2 n+2 делится на 7.
1) Проверим, что эта формула верна при n = 1: 3 2*1+1 +2 1+2 = 3 3 +2 3 =35, 35 кратно 7.
2) Пусть эта формула верна для n = k, т. е. 3 2 k +1 +2 k +2 делится на 7.
3) Докажем, что формула верна и для n = k + 1, т. е.
4) Оба условия принципа математической индукции выполнены, следовательно, предложение истинно при всех значениях n.
Многие задачи на доказательство в теории делимости натуральных чисел удобно решать с применением метода математической индукции, можно даже сказать, что решение задач данным методом вполне алгоритмизировано, достаточно выполнить 4 основных действия. Но универсальным этот метод назвать нельзя, т. к. присутствуют и недостатки: во-первых, доказывать можно только на множестве натуральных чисел, а во-вторых, доказывать можно только для одной переменной.
Для развития логического мышления, математической культуры этот метод является необходимым инструментом, ведь ещё великий русский математик А. Н. Колмогоров говорил: «Понимание и умение правильно применять принцип математической индукции, является хорошим критерием логической зрелости, которая совершенно необходима математику».
1. Виленкин Н. Я. Индукция. Комбинаторика. — М.: Просвещение, 1976. — 48 с.
2. Генкин Л. О математической индукции. — М., 1962. — 36 с.
3. Соломинский И. С. Метод математической индукции. — М.: Наука, 1974. — 63с.
4. Шарыгин И. Ф. Факультативный курс по математике: Решение задач: Учеб.пособие для 10 кл. сред.шк. — М.: Просвещение, 1989. — 252 с.
5. Шень А. Математическая индукция. — М.: МЦНМО,2007.- 32 с.