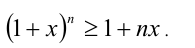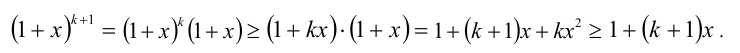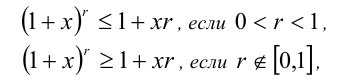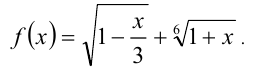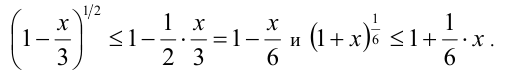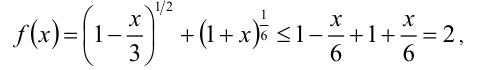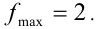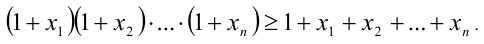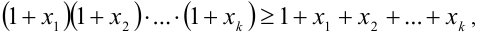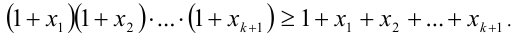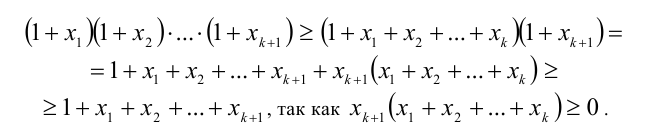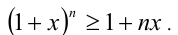Доказать что если x 1 то справедливо неравенство
Доказать что если x 1 то справедливо неравенство
x ≥ –1, n – натуральное число. Докажите, что (1 + x) n ≥ 1 + nx.
Решение 1
Докажем неравенство индукцией по n.
База. При n = 1 неравенство превращается в равенство.
Шаг индукции. Пусть уже доказано, что (1 + x) n ≥ 1 + nx. Тогда (1 + x) n+1 ≥ (1 + nx)(1 + x) = 1 + nx + x + nx² ≥ 1 + (n + 1)x.
Решение 2
3. Из решения 2 видно, что неравенство верно и при нецелых n > 1.
Источники и прецеденты использования
| книга | |
| Автор | Генкин С.А., Итенберг И.В., Фомин Д.В. |
| Год издания | 1994 |
| Название | Ленинградские математические кружки |
| Издательство | Киров: «АСА» |
| Издание | 1 |
| глава | |
| Номер | 16 |
| Название | Неравенства |
| Тема | Алгебраические неравенства и системы неравенств |
| задача | |
| Номер | 056 |
| книга | |
| Автор | Алфутова Н.Б., Устинов А.В. |
| Год издания | 2002 |
| Название | Алгебра и теория чисел |
| Издательство | МЦНМО |
| Издание | 1 |
| глава | |
| Номер | 1 |
| Название | Метод математической индукции |
| Тема | Индукция |
| параграф | |
| Номер | 2 |
| Название | Тождества, неравенства и делимость |
| Тема | Индукция (прочее) |
| задача | |
| Номер | 01.032 |
Неравенства Бернулли
Неравенства Бернулли
Бернулли Якоб (1654-1705) — швейцарский учёный, профессор Базель-ского университета (Швейцария). Известен своими работами по дифференциальной геометрии, вариационному исчислению и математической физике.
Теорема 1 (неравенство Бернулли с натуральным показателем). При любом действительном x (x > — 1) и при любом натуральном n справедливо неравенство
Доказательство. Воспользуемся для доказательства методом полной математической индукции (по параметру n ).
1) При n=1 имеем: 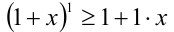
Сформулируем без доказательства неравенство Бернулли в случае, когда показатель степени в неравенстве не является натуральным.
Теорема 2 (неравенство Бернулли с произвольным показателем). Пусть 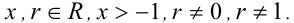
причём неравенства обращаются в равенства только при x = 0.
Пример №135.
Найти наибольшее значение функции
Решение:
Дважды воспользуемся на области определения функции неравенством Бернулли:
Складывая эти неравенства, получаем неравенство
причём равенство достигается при x = 0 (в каждом из двух неравенств). Поэтому f(о) = 2 — наибольшее значение функции.
Ответ:
Рассмотрим, наконец, обобщённое неравенство Бернулли для нескольких действительных чисел.
Теорема 3 (неравенство Бернулли для n чисел). Пусть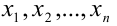
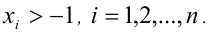
Доказательство (методом математической индукции).
1) При n = 1 неравенство, очевидно, выполняется.
и докажем, что тогда оно выполняется и при n = k + 1, т.е.
В частности, при 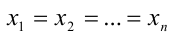
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института