Доказать что inf x sup x

Доказать, что множества чисел бесконечны
доброго времени суток. Объясните мне пожалуйста, с чего вообще начинается доказательство кагого.

Доказать, что противоположные стороны четырёхугольника равны между собой.
1. диагонали четырехугольника пересекаются в точке О, причем одна из диагоналей этой точкой.

У вас путаное объяснение и вы не учитываете возможность бесконечности, но принцип правильный.

Действуйте ясно. Вам требуется доказать, что нижняя грань некоторого множества будет равна такому-то числу. По определению для этого нужно убедиться, что 1) данное число является нижней границей; 2) никакое число, большее данного, не является нижней границей.

Даны два множества. Найти произведение элементов одновременно принадлежащим обоим множествам.
Даны два множества. Найти произведение элементов одновременно принадлежащим обоим множествам.

Доказать что множества эквивалентны
Докажите, что множества А= <точки на параболе>и В= <точки эллипса>эквивалентны на пополненной.

Доказать, что мощность множества счетна
Здравствуйте. Как доказать, что мощность множества рациональных чисел счетна?

Источник

Доказать что inf x sup x

Доказывать надо для верхней грани, так как доказательство для нижней аналогичное.

Рассмотрите два случая:

Для первого случая докажите, что наибольший элемент и является наименьшей верхней границей. Доказывать надо от противного.

Пункт а)

Доказывать будем в обратную сторону, то есть

Нужно доказать два пункта:

Доказательство 1

Докажем, что − sup < x >является нижней границей < − x >, то есть

Будем доказывать от противного:

Так как y ∈ < − x >, то − y ∈ < x >(по определению множеств < x >и < − x >).

Из определения sup < x >:

Но − y тоже принадлежит < x >, поэтому неравенство должно выполняться и для него тоже:

Получаем два противоречащих друг другу неравенства:

Итак, мы показали, что

То есть, − sup < x >является нижней границей множества < − x >.

Доказательство 2

По определению sup < x >:

∀ ε > 0 ∃ x ′ ∈ < x >: x ′ > sup < x >− ε

Неравенство в конце умножим на − 1 :

∀ ε > 0 ∃ x ′ ∈ < x >: − x ′ − sup < x >+ ε

Но если x ′ ∈ < x >, то y ′ = − x ′ принадлежит < − x >(по определению множеств < x >и < − x >).

Поэтому верно следующее

∀ ε > 0 ∃ y ′ ∈ < − x >: y ′ − sup < x >+ ε

Пункт б)

Доказывать будем в обратную сторону, то есть

Нужно доказать два пункта:

Доказательство 1

Докажем, что − in f < x >является верхней границей < − x >, то есть

Будем доказывать от противного:

Умножим неравенство в конце на − 1 :

Так как y ∈ < − x >, то − y ∈ < x >(по определению множеств < x >и < − x >).

Из определения in f < x >:

Но − y тоже принадлежит < x >, поэтому неравенство должно выполняться и для него тоже:

Получаем два противоречащих друг другу неравенства: in f < x >≤ − y − y in f

Итак, мы показали, что

То есть, − in f < x >является верхней границей множества < − x >.

Доказательство 2

По определению in f < x >:

∀ ε > 0 ∃ x ′ ∈ < x >: x ′ in f < x >+ ε

Неравенство в конце умножим на − 1 :

∀ ε > 0 ∃ x ′ ∈ < x >: − x ′ − in f < x >− ε

Но если x ′ ∈ < x >, то y ′ = − x ′ принадлежит < − x >(по определению множеств < x >и < − x >).

Поэтому верно следующее

∀ ε > 0 ∃ y ′ ∈ < − x >: y ′ − in f < x >− ε

Источник

Существование верхней (нижней) грани.

Докажем еще одну теорему, которая опирается на свойство непрерывности действительных чисел.

Терема о существовании верхней (нижней) грани.Сначала введем несколько определений.

Определение. Числовое множество X называется ограниченным, если оно ограничено сверху и снизу.

В символической записи эти определения будут выглядеть следующим образом:

ограничено снизу, если ∃m ∀x ∈ X : x ≥ m и

Пустое множество будем считать ограниченным по определению.

Определение. Для любого числа a R неотрицательное число

называется его абсолютной величиной или модулем. Для абсолютных величин чисел справедливо неравенство |a+b|

Теорема 4.3.1. Числовое множество X ограничено тогда и только тогда, когда существует число C такое, что для всех элементов x из этого множества выполняется неравенство 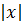≤ C.

Очевидно, что равенство 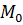= sup X равносильно двум условиям:

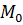
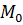
1) ∀x ∈ X выполняется неравенство x ≤ , т.е. — верхняя граница множества X ;

1) ∀x ∈ X выполняется неравенство x ≥ ;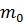

2) ∀ε > 0 ∃xε ∈ X так, что выполняется неравенство xε

Чтобы доказать противоположное неравенство, возьмем число y

Источник

Точные грани числовых множеств

Верхняя и нижняя грани числовых множеств.

Множество X вещественных чисел (X ⊂ \(\mathbb\)) называется ограниченным сверху, если существует вещественное число C такое, что все элементы множества X не превосходят C, то есть
$$
\exists C \ \in \ \mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \leq \ C.\label
$$

Всякое вещественное число C, обладающее свойством \eqref, называется верхней гранью числового множества X.

Аналогично, множество X ⊂ \(\mathbb\) называется ограниченным снизу, если
$$
\exists C’\in\mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \geq \ C’.\label
$$

Всякое вещественное число С ‘ , удовлетворяющее условию \eqref, называют нижней гранью числового множества X.

Если числовое множество множество ограничено как сверху, так и снизу, его называют ограниченным, то есть <X — ограниченное множество>\(\Leftrightarrow\left\ <\exists C’\in \ \mathbb\ \exists C\in\mathbb: \ \forall x\in X \ \rightarrow \ C’ \ \leq \ x \ \leq \ C\right\>\).

Записать ⌉A с помощью кванторов, если A = <C — верхняя грань множества X ⊂ \(\mathbb\)>.

По условию \(B=\left\<\exists C \ \in \ \mathbb: \ \forall x \ \in \ X \ \rightarrow \ x \ \geqslant \ C\right\>\). Поэтому
$$
\rceil B=\left\<\forall C \ \in \ \mathbb: \ \exists x_C \ \in \ X \ \rightarrow \ x_C Определение 1.

Число M называется точной верхней гранью числового множества X, если выполняются следующие условия:

Число M = sup X, вообще говоря, может как принадлежать, так и не принадлежать множеству X. Например, если X — множество чисел x таких, что 1 ≤ x Замечание 2.

Из определения точной верхней грани множества следует, что если у числового множества X есть точная верхняя грань M, то она единственна.

Число m называется точной нижней гранью числового множества X, если выполняются следующие условия:

Если непустое множество вещественных чисел X ограничено сверху, то существует sup X; если непустое множество X ограничено снизу, то существует inf X.

Докажем существование верхней точной грани. По условию множество X не пусто, то есть содержит хотя бы один элемент. Возможны два случая:

Первый случай. Предположим, что все элементы множества X неотрицательны. По условию множество X ограничено сверху, а значит выполняется условие \eqref. Пусть C=c₀,c₁c₂…c_n…; тогда c₀ — неотрицательное целое число, причем C x’.\label$$

Возьмем произвольное число x ∈ X и пусть x = a₀,<a_n>. Чтобы проверить выполнение условия \eqref, рассмотрим три произвольных случая:

$$x\not\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label$$

$$x\in X_k \ \ \ \ \ при \ k=0,1,2,…,\label$$

$$\exists m: \ x\in X_, \ x\not\in X_\label$$

Из \eqref следует, что \(a_0 удовлетворяет произвольный элемент \(\widetilde x\in X_m\), так как

Из неравенства \eqref следует, что sup X есть нижняя грань множества Y. Точная нижняя грань множества Y, то есть число inf Y, есть наибольшая из всех нижних граней множества Y. Значит, sup X ≤ inf Y.

Источник

Пусть множество всех произведений xy, где x принадлежит , а y принадлежит . Причем x>=0 y>=0

C cуммой я вроде справился, а тут совсем непонятно

задан 24 Сен 12:55

sanyapp
25 ● 1 ● 5
77&#037 принятых

@sanyapp: под всегда понимается одноэлементное множество, состоящее из x. То есть исправление всё равно некорректное.

Для случая неотрицательных чисел утверждение очевидно, и доказывается точно так же, как и для суммы.

@caterpillar не понял про нестрогое неравенство @falcao формулировка такая дана в демидовиче, то что xy (24 Сен 16:24) sanyapp

@sanyapp, приведите свои рассуждения для случая суммы. Чтобы стало понятнее, в каком месте Вы не видите, что они повторяются и для произведения. И я не писал про нестрогое неравенство. Я писал про строгое.

@sanyapp: а можно ссылку на страницы задачника?

Доказательство в другую сторону (на содержательном уровне) такое: полагаем a=sup X, b=sup Y. Берём eps > 0. Находим в X точку x > a-eps. В Y находим точку y > b-eps. Тогда при достаточно малом eps будет xy > (a-eps)(b-eps). Устремляем eps к нулю (справа). Это даст sup(XY)>=ab.

@caterpillar: я хотел своими глазами такие обозначения увидеть. Жаль, что в переизданиях классического задачника оставляют явную «архаику».

@sanyapp: если пределы пока не изучались, то достаточно рассмотреть разницу между числами и оценить её сверху: ab-(a-eps)(b-eps) (24 Сен 23:37) falcao

@falcao cтраница 11 http://pm-pu.ru/stuff/analiz/books/demidovich_sbornik.pdf на 8мой странице есть определение sup и inf, с 1 пунктом у меня получилось, а вот второй пункт пока нет. Мне надо как-то показать, что для любого еps>0 сущ. x’y’ принадл. что supsup — eps (25 Сен 14:19) sanyapp

Ну, считайте, что c=ab-eps. При рассуждении от противного это будет мажорантой (да, верхней границей) для XY. Но это вполне бессмысленное занятие так расписывать.

@sanyapp: выше всё было подробно расписано с участием eps на вполне формальном уровне.

Источник