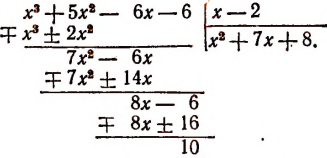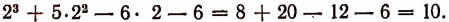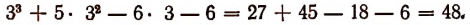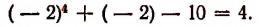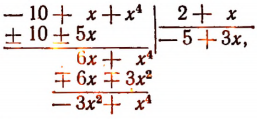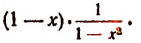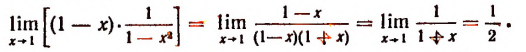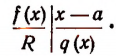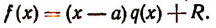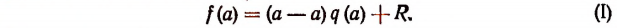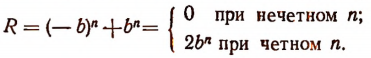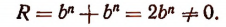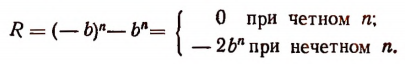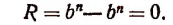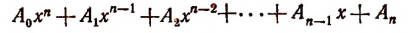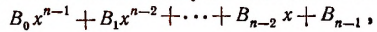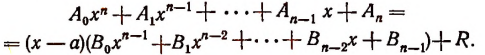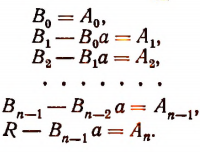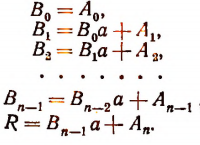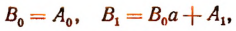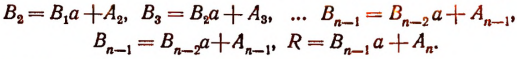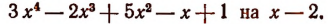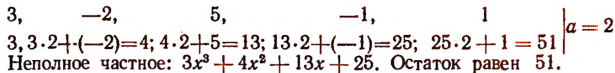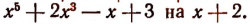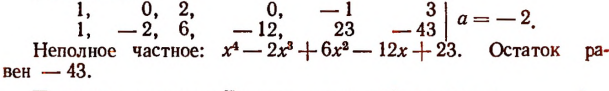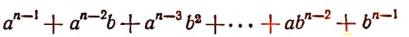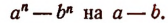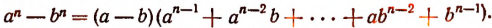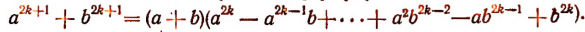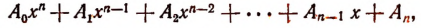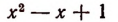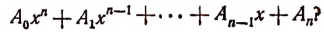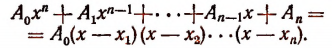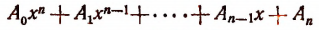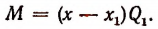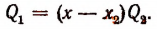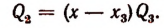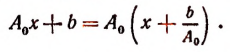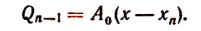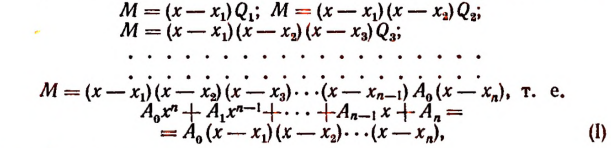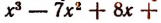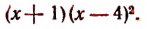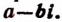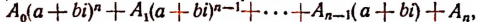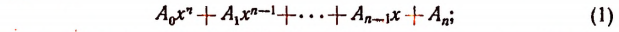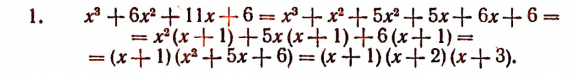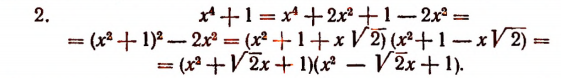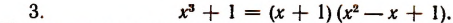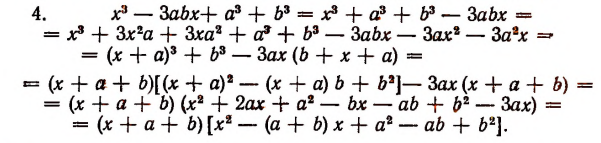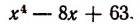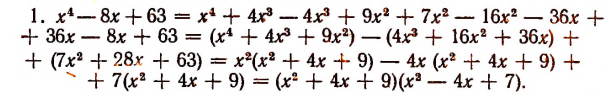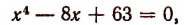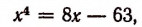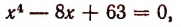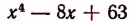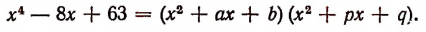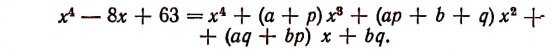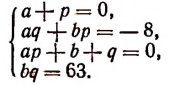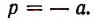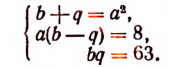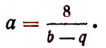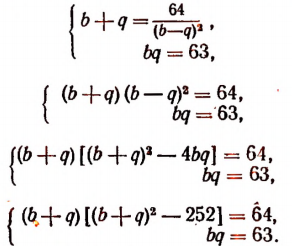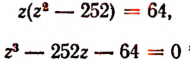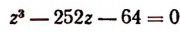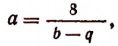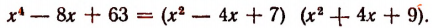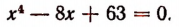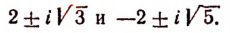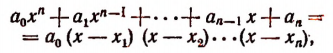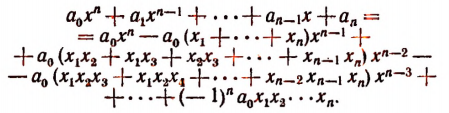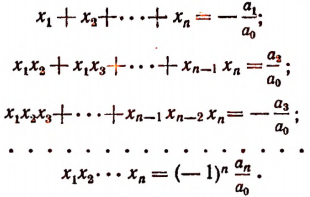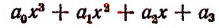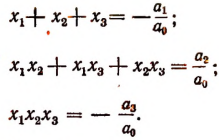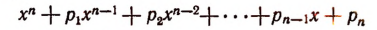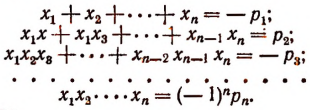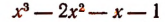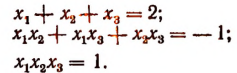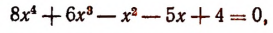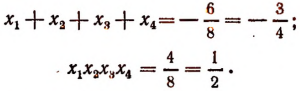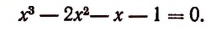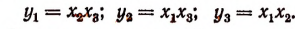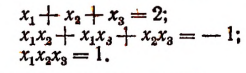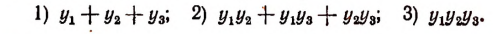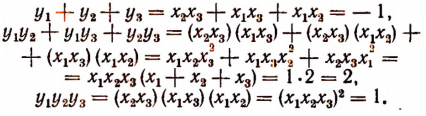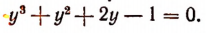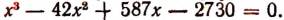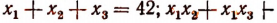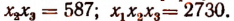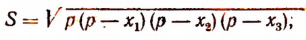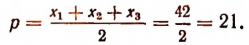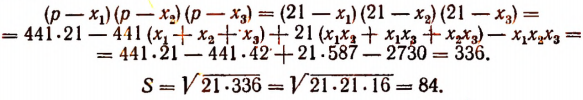Доказать что многочлен делится на многочлен
Класс: 11
Презентация к уроку
Цель урока:
Тип урока: урок ознакомления с новым материалом.
Оборудование: мультимедиа проектор, презентация к уроку, компьютерный класс.
Ход урока
I. Организационный момент
Наша задача сегодня в совместной деятельности подтвердить слова Декарта (слайд 1). Тема нашего урока (слайд 2) «Теорема Безу» настолько значима, что даже используется в заданиях ЕГЭ и различных олимпиадах. Теорема Безу облегчает решение многих заданий, содержащих уравнения высших степеней. К сожалению, она изучается только на профильном уровне.
II. Возникновение проблемной ситуации
На этом уроке мы научимся решать уравнения высших степеней, а алгоритм решения выведем сами.
III. Актуализация опорных знаний
(По формуле разложения на множители квадратного трехчлена:
ах 2 + bх + с = a(x – x1)(x-x2), где х1 и х2 корни трехчлена).
Найдите корни трехчлена двумя способами. Какими?
(по формуле корней квадратного уравнения и по теореме Виета).
Это значит, что трехчлен делится на каждый из двучленов: х – 6 и х + 1.
Обратите внимание на свободный член нашего трехчлена и найдите его делители (±1, ±2, ±3, ±6).
Какие из делителей являются корнями трехчлена? (-1 и 6)
Какой вывод можно сделать? (Корни трехчлена являются делителями свободного члена).
IV. Выдвижение гипотезы
Так какой же одночлен поможет подобрать корни многочлена?
Выпишите его делители: ±1; ±2; ±4.
Найдите значения многочлена для каждого делителя. С помощью электронных таблиц и непосредственно:
Лекция по теме»Делимость многочленов»
Муниципальное бюджетное общеобразовательное учреждение
Средняя общеобразовательная школа п. Надвоицы
Тема: ДЕЛИМОСТЬ МНОГОЧЛЕНОВ
Забровская Алина, Зотикова Елена, Степанович Арина, обучающиеся 8 «а» класса МБОУ СОШ п. Надвоицы
Руководитель: Шалагинова Людмила Сергеевна, учитель математики
Действия с многочленами
2.1 Сложение (вычитание) многочленов
2.2 Умножение многочленов
3.1 Свойства теории делимости многочленов
3.2 Деление многочленов столбиком
Применение теории делимости
4.2 Разложение на множители
4.3 Сокращение дробей
4.4 Решение уравнений
Применение схемы Горнера при решении уравнений с параметром
Список используемой литературы и ссылки
В работе рассматриваются основы теории делимости многочленов и её применение. Кратко рассказывается об истории возникновения теории делимости. В работе представлены формулировки и основные понятия теории делимости многочленов. Показан основой принцип деления и его приложения.
Эта тема выбрана, потому что на уроках алгебры мы изучали сложение, вычитание, умножение многочленов, а вот деление многочленов нет.
Цель нашей работы : изучить теорию делимости многочленов и области ее применения.
Для достижения этой цели мы изучили основные понятия, теоремы и алгоритмы теории делимости. С помощью основ теории делимости многочленов можно делить многочлены, раскладывать многочлены на множители, решать уравнения, сокращать дроби, решать математические задачи.
Изучить основные понятия, теоремы и алгоритмы теории делимости.
Показать использование теории делимости многочленов в решении алгебраических задач.
Создать обучающие видеоуроки для учащихся по данной теме проекта.
Подобрать задачи для самостоятельного решения для учащихся 8-11 классов на применение теории делимости многочленов.
Применение теории делимости многочленов является важной частью работы: теорема Безу и её следствие, разложение многочленов на множители, сокращение дробей, решение уравнений. Поэтому в работе есть задачи на применение теории делимости многочленов и задания для самостоятельного решения.
Методами исследования являлись: анализ учебной и дополнительной литературы, собственный анализ.
В нашей работе представлены обучающие видеоуроки, где рассматриваются основы теории делимости многочленов. Они позволят разобраться ученикам в задачах, которые сложно решить, не зная данной теории. Также в работе представлен наш отчёт о проведённых уроках в некоторых классах нашей школы.
*Данный многочлен можно привести к стандартному виду. Говорят, что многочлен имеет стандартный вид, если все его члены записаны в стандартном виде и среди них нет подобных: 17aуу– 7ay 2 +5aуу+a =17ay 2 – 7ay 2 +5ay 2 +а=15ay 2 +а
Многочлены, которые состоят из двух и трех членов, имеют специальные названия – двучлен и трехчлен соответственно. Так х+у – это двучлен, а 2x 3 q−qx 2 +7b – трехчлен.
В своей работе мы будем использовать многочлены стандартного вида первой степени, второй, третьей и четвёртой. (Степенью многочлена называют наибольшую из степеней входящих в него одночленов).
2. Действия с многочленами
2.1 Сложение (вычитание) многочленов
Суммой (разностью) двух многочленов называется многочлен, коэффициенты которого являются суммой (разностью) коэффициентов при подобных членах этих многочленов.
На практике для нахождения суммы и разности многочленов используют правила раскрытия скобок, перед которыми стоит знак плюс (знак минус).
2.2 Умножение многочленов
Чтобы умножить многочлен на одночлен, нужно умножить каждый член многочлена на этот одночлен и сложить полученные произведения.
Чтобы умножить многочлен на многочлен, нужно умножить каждый член первого многочлена на каждый член второго многочлена полученные одночлены сложить.
3. Делимость многочленов
3.1 Свойства теории делимости многочленов
Теория делимости многочленов имеет следующие свойства:
1) Если P 1 (x) и P 2 (x) делятся на Q(x); то P 1 (x) + P 2 (x) и P 1 (x) _ P 2 (x)делятся на Q(x);
3) Если P(x) делится на Q(x), а Q(x) делится на H(x), то P(x) делится на H(x).
4) Если ненулевой многочлен P(x) делится на Q(x), то deg P(x) ≥ deg Q(x),где deg(Р(x) и Q(x)-степени этих многочленов.
5) Еесли deg P(x) = deg Q(x); то P(x) делится на Q(x) тогда и только тогда, когда эти многочлены пропорциональны (многочлены называются пропорциональными, если один из них получается из другого умножением на число, отличное от 0).
3.2 Деление многочленов столбиком
В алгебре, деление многочленов столбиком — алгоритм деления многочлена f(x) на многочлен g(x), степень которого меньше или равна степени многочлена f(x). Алгоритм представляет собой обобщенную форму деления чисел столбиком, легко реализуемую вручную.
Целью алгоритма деления многочленов в столбик является нахождение частного q(x) и остатка r(x) для заданных делимого f(x) и ненулевого делителя g(x).
Пример: Покажем, что
Частное и остаток от деления могут быть найдены в ходе выполнения следующих шагов:
в). Вычитаем полученный после умножения многочлен из делимого, записываем результат под чертой
г). Повторяем предыдущие 3 шага, используя в качестве делимого многочлен, записанный под чертой.
Первую лекцию о делимости многочленов мы провели в своём 8-а классе. На диаграмме показаны результаты самостоятельной работы «Деление многочлена на двучлен». Из 22 учеников полностью справилось 50% учеников.
Одно из заданий работы
С лекцией о делимости многочленов мы выходили в 8-в, 9-а и 10-б классы. После лекции мы проводили небольшие самостоятельные работы. Результаты работ можно увидеть на диаграммах.




Предлагаем задачи для самостоятельного решения:
1.Выполните деление с остатком многочлена 2 x 2 − 9x − 3 на х-2
Основные труды относятся к решению алгебраических уравнений. В 1819 году опубликовал способ приближённого вычисления действительных корней многочлена, который называется теперь способом Руффини-Горнера (этот способ был известен китайцам еще в XIII веке). Работа была напечатана в философских работах Королевского научного сообщества.
Схема Горнера – способ деления многочлена Р(х) на бином x−a. Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число a, взятое из бинома x−a.
Покажем схему Горнера для многочлена четвёртой степени (частный случай).
Непосредственное применение схемы Горнера проще всего показать на примерах.
Пример №1: Разделить 5x 4 +5x 3 +x 2 −11 на x−1,используя схему Горнера.
Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число 5, просто перенеся его из соответствующей ячейки первой строки:
Следующую ячейку заполним по такому принципу: 1⋅5+5=10:
Аналогично заполним и четвертую ячейку второй строки: 1⋅10+1=11:
Для пятой ячейки получим: 1⋅11+0=11:
И, наконец, для последней, шестой ячейки, имеем: 1⋅11+(−11)=0:
Задача решена, осталось только записать ответ:
Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления 5×4+5×3+x2−11 на x−1. Естественно, что так как степень исходного многочлена 5x 4 +5x 3 +x 2 −11 равнялась четырём, то степень полученного многочлена 5x 3 +10x 2 +11x+11 на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остаток от деления многочлена 5x 4 +5x 3 +x 2 −11 на x−1. В нашем случае остаток равен нулю, т.е. многочлены делятся нацело.
Пример №2 : Разделить многочлен x 4 +3x 3 +4x 2 −5x−47 на x+3 по схеме Горнера.
Решение: Сразу оговорим, что выражение x+3 нужно представить в форме x−(−3). В схеме Горнера будет участвовать именно −3. Так как степень исходного многочлена x 4 +3x 3 +4x 2 −5x−47 равна четырём, то в результате деления получим многочлен третьей степени:
Полученный результат означает, что
x 4 +3x 3 +4x 2 −5x−47 =(x+3)(x 3 +0⋅x 2 +4x−17)+4=(x+3)(x 3 +4x−17)+4
В этой ситуации остаток от деления x 4 +3x 3 +4x 2 −5x−47 на x+3 равен 4.
С лекцией о делимости многочленов по схеме Горнера мы выходили в 8-в и 11 классы. После лекции мы проводили небольшие самостоятельные работы. Результаты работ можно увидеть на диаграммах.
Одно из заданий работы
Одно из заданий работы
Предлагаем задачи для самостоятельного решения:
1.Разделить многочлен 
2.Разделить многочлен 

4. Применение теории делимости
Дата рождения: 31 марта 1730 г
Место рождения: страна Франция, Немур.
Дата смерти:27 сентября 1783.
Научная сфера: теория чисел.
Что и требовалось доказать.
Важнейшим следствием теоремы Безу является то, что корни целочисленного многочлена являются делителями его свободного члена.
Задачи на применение теоремы Безу и следствия из теоремы:
1. Найти остаток от деления многочлена 

Решение: Исходя из теоремы Безу, искомый остаток соответствует значению многочлена в точке 




Ответ: остаток равен 5.
2. Найти значение f (x) = x 3 − 3x 2 + 7x − 5 в точке 3.
Решение : Напомним теорему Безу: Значение многочлена f (x) в точке c равно остатку от деления f (x) на (x − c). Разделим f (x) = x 3 − 3x 2 + 7x – 5 на х-3:
Предлагаем задачи для самостоятельного решения:
2. Найти корни многочлена по схеме Горнера: f (x) = x 3 + 2 x 2 – 5 x – 6.
Разложение на множители
Запись нашего решения:
Предлагаем задачи для самостоятельного решения:
Разложить на множители многочлены:
Теорема Безу и ее применение в математике с примерами решения
Иллюстрация теоремы Безу на примерах:
Пусть требуется, например, разделить многочлен 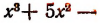
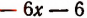
Можно предсказать, что остаток при этом делении будет равен 10. Проверим это:
Предсказание было сделано следующим образом.
Рассматривая делитель х—2, мы видим, что в нем из независимой переменной х вычитается число 2. Это число 2 мы подставили в делимое вместо переменного х и получили 10, т. е. как раз остаток.
Таким образом, оказалось, что остаток от деления многочлена на х—2 равен значению делимого при х = 2.
Это правило определения остатка, сформулированное в общем виде, и будет являться теоремой Безу.
При делении многочлена 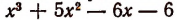
(Проверьте это непосредственным делением.)
При делении многочлена 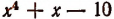
(Проверьте это непосредственным делением.)
При делении многочлена 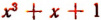
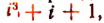
Приведенные примеры никак не могут рассматриваться как доказательства теоремы Безу: они даны лишь для того, чтобы облегчить понимание самой формулировки теоремы Безу.
Формулировка и доказательство теоремы Безу
При делении многочлена п-й степени относительно х, расположенного по убывающим степеням х, на двучлен (х — а остаток равен значению делимого при х = а
буква а может обозначать любое действительное или мнимое число, т. е. любое комплексное число).
Прежде чем доказывать теорему, сделаем несколько подготовительных пояснений.
1. В формулировке теоремы не случайно сказано: «расположенного по убывающим степеням х».
Если производить деление, расположив делимое и делитель по возрастающим степеням х, то тогда нельзя утверждать, что остаток всегда будет равен значению делимого при х = а.
Например, если многочлен 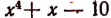
то мы никогда не получим остатка, равного числу 4, т. е. значению делимого при x = — 2.
2. Мы знаем, что существуют такие алгебраические выражения, которые теряют смысл при некоторых отдельных значениях входящих в него букв. Например, 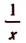
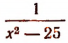
Заметим, что многочлен любой целой положительной степени никогда не теряет смысла. При всяком значении переменной он принимает определенное значение.
3. Произведение двух множителей, из которых один обращается в нуль, а другой принимает определенное значение, всегда равно нулю. Если же один множитель обращается в нуль, а другой теряет смысл, то о таком произведении нельзя говорить, что оно равно нулю. О таком произведении ничего определенного сказать нельзя. В каждом отдельном случае необходимо особое исследование.
Рассмотрим, например, произведение
При х = 1 первый множитель обращается в нуль, а второй теряет смысл. Нельзя утверждать, что это произведение при х = 1 равно нулю.
Итак, при х = 1 само произведение 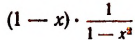
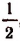
Доказательство теоремы Безу
Пусть f(x) обозначает собой произвольный многочлен n-й степени относительно переменной х, расположенный по убывающим степеням х, и пусть при делении на двучлен х — а получилось в частном q(x), а в остатке R (см. схему деления):
Очевидно, что q(х) будет некоторый многочлен (п — 1)-й степени относительно х, а остаток R будет величиной постоянной, т. е. не зависящей от х.
Если бы остаток R был многочленом хотя бы первой степени относительно х, то это означало бы, что процесс деления не доведен до конца. Итак, R от х не зависит
По свойству деления (делимое равно произведению делителя на частное плюс остаток) получим тождество
Это равенство справедливо прн всяком значении х, значит, оно будет справедливым и при х = а.
Подставляя в левую и правую части этого равенства вместо переменной х число а, получим:
Здесь символ f(a) обозначает собой уже не f(x) т.е. не многочлен относительно х, а значение этого многочлена при х = a.
q(а) обозначает значение q(x) при х = а.
Остаток R остался таким, каким он был раньше, так как R от х не зависит.
Произведение (а — a)q(a) равно нулю, так как множитель (а — а) равен нулю, а множитель q(a) есть определенное число. (Многочлен q(x) ни при каком определенном значении х не теряет смысла.)
Поэтому из равенства (I) получим:
что и требовалось доказать.
Пример:
При делении многочлена 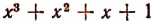
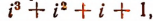
Следствия из теоремы Безу
Следствие 1. Если многочлен делится без остатка на х — а, то а необходимо будет корнем этого многочлена.
Следствие 2. Если а есть корень какого-либо многочлена, то это условие будет достаточным для делимости этого многочлена без остатка на х — а.
Эти два следствия можно объединить и выразить следующим образом:
Для делимости многочлена на x — а необходимо и достаточно, чтобы а было корнем этого многочлена.
Применения теоремы Безу
Поинтересуемся делимостью выражений вида 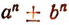
В выражении 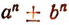
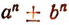
а) При делении 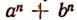
Значит, 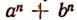
б) При делении 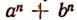
Значит, 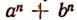
в) При делении 
Значит, 
г) При делении 
Значит, 
Другие важные применения теоремы Безу изложены в следующих главах.
Правило Горнера. Правило Горнера позволяет вычислять коэффициенты частного и остаток при делении многочлена, расположенного по убывающим степеням х, на двучлен х — а, не производя самого деления. При делении многочлена
на двучлен x — а в частном получим многочлен степени (п — 1):
а в остатке — некоторое число R.
По свойству деления
Раскрыв скобки в правой части этого равенства и объединив члены с одинаковыми степенями х, получим тот же многочлен, что и в левой части.
Приравнивая коэффициенты при одинаковых степенях х, найдем, что
Вычисления можно располагать так: коэффициенты делимого:
коэффициенты частного и остаток:
Примеры:
1. С помощью правила Горнера найти частное и остаток при делении многочлена
Решение:
2. Разделить
Решение:
Пользуясь правилом Горнера, легко найти частное
Отсюда вытекает формула
Аналогично можно получить и формулу
Теорема Гаусса
Если бы мы не знали никаких других чисел, кроме натуральных, то сказали бы, что уравнение 2х— 3 = 0 не имеет ни одного корня, так как нет ни одного натурального числа, которое удовлетворяло бы этому уравнению.
Уравнение 2х + 3 =0 не имеет ни одного корня в области положительных чисел.
Уравнение 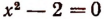
Уравнение 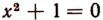
Выражение
в котором х есть независимая переменная, 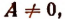
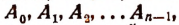
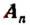
Корнем данной целой рациональной функции называется такое значение (действительное или мнимое) переменной х, при котором эта целая рациональная функция обращается в нуль.
В области действительных чисел не всякая целая рациональная функция имеет корень. Например, целая рациональная функция
не имеет ни одного действительного корня.
В связи с этим возникает следующий важный вопрос. Можно ли утверждать, что среди комплексных чисел найдется хоть одно число, являющееся корнем целой рациональной функции
Этот вопрос на протяжении длительного исторического периода оставался неразрешенным. В 1799 году Гаусс в возрасте 22 лет дал первое строгое доказательство теоремы о существовании корня целой рациональной функции.
Теорема Гаусса гласит: Всякая целая рациональная функция с любыми комплексными коэффициентами имеет по крайней мере один корень (действительный или мнимый).
В настоящее время существует несколько различных доказательств этой фундаментальной теоремы алгебры, но все они сложны и не входят в курс элементарной алгебры.
Теорема Гаусса еще раз свидетельствует нам ту общность в решении различных вопросов, которую придает им введение в науку комплексных чисел.
Свойства целой рациональной функции
Теорема Гаусса позволяет открыть и доказать другие важные свойства целой рациональной функции.
1. Всякую целую рациональную функцию п-й степени можно представить в виде произведения коэффициента высшего члена на п линейных множителей, т. е.
Эти линейные множители могут быть все действительными или все мнимыми и могут быть частью действительными и частью мнимыми.
Доказательство:
обозначим для краткости буквой М. По теореме Гаусса М имеет по крайней. мере один корень х, (действительный или мнимый). Тогда по следствию из теоремы Безу многочлен М должен делиться без остатка на 
Обозначив буквой 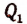
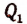
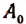
По теореме Гаусса функция 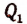
Обозначив этот корень буквой 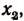
Число 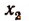
Применяя такие же рассуждения к функции 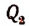
Степени функций 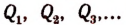
Продолжая этот процесс, мы придем к равенству
где 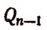
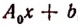
Обозначив корень функции 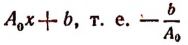

Пользуясь полученными равенствами, найдем последовательно:
что и требовалось доказать.
Из равенства (I) непосредственно видно, что числа 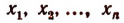
Правая часть равенства (I) не может обратиться в нуль ни при каком значении переменной х, отличном от значений
Следовательно, целая рациональная функция п-й степени не может иметь более п корней.
Если все числа 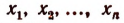
Если же среди чисел 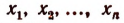
Пусть оказалось, что
а остальные корни отличны от 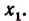
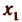
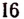
Значит, число — 1 есть простой ксрень, а число 4 есть корень кратности 2 или двукратный корень.
2. Если целая рациональная функция с действительными коэффициентами имеет комплексный корень 
в котором 
Заменив в последнем равенстве i числом —i, получим:
Теперь допустим, что 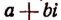
тогда окажется, что P + Qi = 0. Отсюда следует, что Р = 0 и Q = 0. Но в таком случае окажется равным нулю и выражение Р—Qi, т. е. окажется корнем целой рациональной функции (1) и число 
3. Всякая целая рациональная функция с действительными коэффициентами степени выше 2-й разложима либо на действительные линейные множители, либо на действительные множители 2-й степени, либо на действительные множители, среди которых имеются и линейные и второй степени. (Доказательство 3-го свойства опускается.)
Примеры разложения целой рациональной функции с действительными коэффициентами степени выше второй на действительные неприводимые множители
Получилось разложение на действительные линейные множители.
Получилось разложение на действительные множители 2-й степени.
Получился один множитель линейный, а другой 2-й степени.
Получился один множитель линейный, а другой 2-й степени.
Теоретически доказано (как уже отмечалось), что всякая целая рациональная функция с действительными коэффициентами степени выше 2-й разложима на действительные множители 1-й и 2-й степени.
Однако осуществление этого разложения не всегда достигается легко. Например, попробуем разложить на множители
Решим эту задачу двумя способами.
(Полученные многочлены 2-й степени имеют мнимые корни, а потому неразложимы на действительные линейные множители.)
Изложенный способ носит слишком искусственный характер. Его трудно придумать.
Второй способ, изложенный ниже, будет менее искусственным.
2. Прежде всего исследуем характер корней многочлена 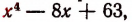
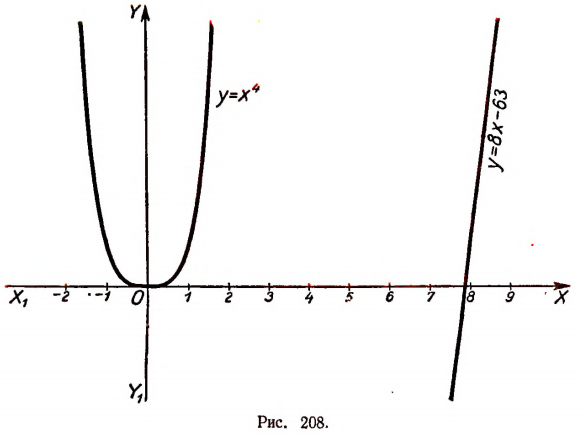
Переписав это уравнение в виде
построим графики функций 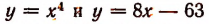
а значит, и многочлена
будут все мнимыми. Поэтому среди действительных множителей, на которые разлагается этот многочлен, не может быть ни одного линейного.
Итак, выяснено, что действительными множителями разложения многочлена 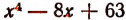
Таким образом, будем иметь, что
Остается определить а, b, р и q.
Перемножив многочлены, стоящие в правой части последнего равенства, получим:
Но поскольку нам необходимо, чтобы правая часть этого равенства превратилась в такой же многочлен, который стоит в левой части, потребуем выполнения следующих условий:
Получилась система четырех уравнений с четырьмя неизвестными a, b, р, q.
Из первого уравнения
Подставив во второе и третье уравнение — а вместо р, получим систему:
Из второго уравнения этой системы
Подставив это в первое уравнение, получим систему:
Обозначим b + q буквой z. Тогда первое уравнение последней системы примет вид:
Делителями числа 64 являются: ± 1; ± 2; ± 4; ± 8; ± 16; ± 32; ± 64.
Испытывая эти делители, обнаружим, что число 16 является корнем уравнения
Значит, мы можем взять b + q = 16. Кроме того, bq = 63. Отсюда примем b = 7 и q = 9. Пользуясь равенством
получим, что а = —4. Наконец, из равенства р = —а найдем, что р = — 4.
Теперь задача решена полностью. Мы получили:
Имея это разложение, мы легко обнаруживаем все корни многочлена 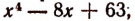
Этими корнями будут комплексные числа
Формулы Виета
Было доказано, что целая рациональная функция разлагается иа множители по формуле:
где 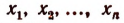
Сравнивая коэффициенты при одинаковых степенях буквы х в левой и правой частях последнего равенства, получим формулы:
Эти формулы носят название формул Виета, по имени открывшего их замечательного французского математика Франсуа Виета. Оии связывают корни и коэффициенты целой рациональной функции. Например, для
Для приведенной функции
формулы Виета принимают вид:
Примеры:
1. Не решая уравнения
найти сумму и произведение его корней.
Решение:
2. Пусть 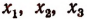
Составить новое уравнение, корнями которого были бы числа:
Решение:
Согласно формулам Виета
Теперь найдем значения трех выражений:
Искомым уравнением будет
3. Сторонами треугольника являются корни уравнения
Не решая этого уравнения, найти площадь треугольника.
Решение:
Обозначим корни данного уравнения через 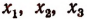
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института