Доказать что множества эквивалентны

Эквивалентность множеств

Определение 1.2. Если каждому элементу множества A сопоставлен единственный элемент множества B и при этом всякий элемент множества B оказывается сопоставленным одному и только одному элементу множества A, то говорят, что между множествами A и B существует взаимно однозначное соответствие. Множества A и B в этом случае называют эквивалентными или равномощными.

Эквивалентность множеств обозначается следующим образом: A

Эквивалентность множеств обладает следующим свойством транзитивности.

Докажем это свойство. Так как A

B, то для всякого элемента a Î А существует единственный элемент b Î B. Но так как B

C, то для всякого элемента b Î B существует единственный элемент c Î C. Сопоставим этот элемент элементу a Î А. Значит, для всякого элемента a Î А существует единственный элемент c Î C и для всякого элемента c Î C существует единственный элемент a Î А. Следовательно, A

Очевидно, что два конечных множества эквивалентны тогда и только тогда, когда количество элементов в них одинаково. Например, множества А = <4, 5, 6>и В = <x, y, z> эквивалентны, A

B. Взаимно однозначное соответствие может быть установлено между элементами 4 и x, 5 и y, 6 и z.

Мощностью конечного множества А (обозначается çАç) называется число элементов этого множества. Например, мощность множества А = <1, 2>равна çАç= 2.

Рассмотрим задачу определения мощности объединения n конечных множеств.

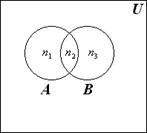
Пусть n = 2 и A и B – два пересекающихся множества. Докажем с помощью диаграммы Эйлера – Венна следующее соотношение:

Из рис. 1.3 видим, что

Формула (1.1) справедлива и для случая, если множества A и B не пересекаются. В этом случае

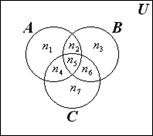
Пусть n = 3 и A, B и С – три пересекающихся множества. В этом случае справедливо следующее соотношение:

Из рис. 1.4 видим, что

что и доказывает формулу (1.2).

Формула (1.2) справедлива и для случая, если множества A, B и С попарно не пересекаются. В этом случае

В общем случае мощность объединения n множеств определяется по формуле:

Эта формула выводится индукцией по n, [3].

Если множества А_i попарно не пересекаются, т.е. А_i ÇА_j = Æ, i ¹ j,то получим частный случай формулы (1.3):

В общем случае справедливо неравенство

Понятие эквивалентности годится и для бесконечных множеств. Пусть, например, A = <1, 2, 3, …, n,…>, B = <– 1, –2, …, –n, …>. Тогда A

B. Взаимно однозначное соответствие устанавливается по правилу: элементу nÎ A соответствует элемент – nÎ B, т.е. n « – n.

B. Взаимно однозначное соответствие устанавливается по правилу: n « 2 n.

A = <1, 2, 3, …, n,…> – множество натуральных чисел, B = <…, –n, …– 2, –1, 0, 1, 2, …, n, …> – множество всех целых чисел.

Перепишем множество B следующим образом:

B = <0, –1, 1, – 2, 2, …, –n, n, …>, так, что 0 будет на первом месте, –1 на втором, 1 на третьем, –2 на четвертом и т.д. Нетрудно заметить, что отрицательные числа будут стоять на местах с четными номерами, а 0 и положительные числа – на местах с нечетными номерами. Поэтому взаимно однозначное соответствие между множествами A и B устанавливается по правилу: для всякого n ³ 0 элементу a = 2n +1 из множества A (т.е. нечетному элементу) соответствует элемент b = n из множества B; элементу a = 2n из множества A (т.е. четному элементу) соответствует элемент b = –n из множества B. Таким образом, реализуется взаимно однозначное соответствие между множествами A и B: 1 « 0, 2 « –1, 3 « 1, 4 « –2 и т.д.

Примеры 1.18 и 1.19 показывают, что множество может быть эквивалентно своему подмножеству. Так, в примере 1.18 BÌ A, а в примере 1.19 A Ì B. И в том, и в другом случае A

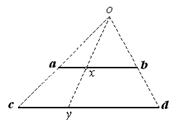
Установить эквивалентность множеств, т.е. установить взаимно однозначное соответствие между их элементами можно различными путями. На рис. 1.5 показано, что множества точек двух отрезков [a, b] и [c, d] эквивалентны.

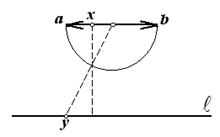
Таким же образом можно установить эквивалентность множеств точек двух интервалов. На рис.1.6 показано, что множества точек любого интервала (a, b) эквивалентно множеству точек всей прямой.

Для установления эквивалентности двух множеств можно применять следующую теорему.

Теорема Бернштейна. Если множество A эквивалентно части множества B, а множество B эквивалентно части множества A, то множества A и B эквивалентны.

Применим теорему Бернштейна для доказательства того, что множество точек любого отрезка эквивалентно множеству точек любого интервала.

Пусть A = [a, b] – произвольный отрезок, а B = (c, d) – произвольный интервал.

Таким образом, выполняются условия теоремы Бернштейна. Поэтому A

Итак, все интервалы, отрезки и вся прямая эквивалентны между собой.

Источник

Теория функций действительного переменного/Эквивалентные множества

Определение: Множество A называется эквивалентным множеству B, если существует биекция f:А→B. В этом случае говорят также, что множество A имеет одинаковую мощность с множеством B. Обозначение:A

Доказательство строится на определении эквивалентного множества и свойств биекции:

B₂,то A 1 × A 2 ∼ B 1 × B 2 <\displaystyle A_<1>\times A_<2>\sim B_<1>\times B_<2>> .

Tеорема 3: Пусть < A x >x ∈ X <\displaystyle \\>_> и < B y >y ∈ Y <\displaystyle \\>_> — два семейcтва попарно непересекающихся множеств, и пусть существует такая биекция: f:X→Y, что A_x

Tеорема 4: Если A 3 ⊂ A 2 ⊂ A 1 <\displaystyle A_<3>\subset A_<2>\subset A_<1>> и A₃

Понятие эквивалентности двух множеств было бы бессодержательным, если б оказалось, что все бесконечные множества эквивалентны между собой. Однако это не так, что и вытекает из следyщей теоремы.

Упражнения [ править ]

1. Установите биекцию между;

2. Доказать, что если A\B

6. Установите биекцию между

Источник

Эквивалентность множеств

Определение 1.2. Если каждому элементу множества A сопоставлен единственный элемент множества B и при этом всякий элемент множества B оказывается сопоставленным одному и только одному элементу множества A, то говорят, что между множествами A и B существует взаимно однозначное соответствие. Множества A и B в этом случае называют эквивалентными или равномощными.

Эквивалентность множеств обозначается следующим образом: A

Эквивалентность множеств обладает следующим свойством транзитивности.

Докажем это свойство. Так как A

B, то для всякого элемента a Î А существует единственный элемент b Î B. Но так как B

C, то для всякого элемента b Î B существует единственный элемент c Î C. Сопоставим этот элемент элементу a Î А. Значит, для всякого элемента a Î А существует единственный элемент c Î C и для всякого элемента c Î C существует единственный элемент a Î А. Следовательно, A

Очевидно, что два конечных множества эквивалентны тогда и только тогда, когда количество элементов в них одинаково. Например, множества А = <4, 5, 6>и В = <x, y, z> эквивалентны, A

B. Взаимно однозначное соответствие может быть установлено между элементами 4 и x, 5 и y, 6 и z.

Мощностью конечного множества А (обозначается çАç) называется число элементов этого множества. Например, мощность множества А = <1, 2>равна çАç= 2.

Рассмотрим задачу определения мощности объединения n конечных множеств.

Пусть n = 2 и A и B – два пересекающихся множества. Докажем с помощью диаграммы Эйлера – Венна следующее соотношение:

Из рис. 1.3 видим, что

Формула (1.1) справедлива и для случая, если множества A и B не пересекаются. В этом случае

Пусть n = 3 и A, B и С – три пересекающихся множества. В этом случае справедливо следующее соотношение:

Из рис. 1.4 видим, что

что и доказывает формулу (1.2).

Формула (1.2) справедлива и для случая, если множества A, B и С попарно не пересекаются. В этом случае

В общем случае мощность объединения n множеств определяется по формуле:

Эта формула выводится индукцией по n, [3].

Если множества А_i попарно не пересекаются, т.е. А_i ÇА_j = Æ, i ¹ j,то получим частный случай формулы (1.3):

В общем случае справедливо неравенство

Понятие эквивалентности годится и для бесконечных множеств. Пусть, например, A = <1, 2, 3, …, n,…>, B = <– 1, –2, …, –n, …>. Тогда A

B. Взаимно однозначное соответствие устанавливается по правилу: элементу nÎ A соответствует элемент – nÎ B, т.е. n « – n.

B. Взаимно однозначное соответствие устанавливается по правилу: n « 2 n.

A = <1, 2, 3, …, n,…> – множество натуральных чисел, B = <…, –n, …– 2, –1, 0, 1, 2, …, n, …> – множество всех целых чисел.

Перепишем множество B следующим образом:

B = <0, –1, 1, – 2, 2, …, –n, n, …>, так, что 0 будет на первом месте, –1 на втором, 1 на третьем, –2 на четвертом и т.д. Нетрудно заметить, что отрицательные числа будут стоять на местах с четными номерами, а 0 и положительные числа – на местах с нечетными номерами. Поэтому взаимно однозначное соответствие между множествами A и B устанавливается по правилу: для всякого n ³ 0 элементу a = 2n +1 из множества A (т.е. нечетному элементу) соответствует элемент b = n из множества B; элементу a = 2n из множества A (т.е. четному элементу) соответствует элемент b = –n из множества B. Таким образом, реализуется взаимно однозначное соответствие между множествами A и B: 1 « 0, 2 « –1, 3 « 1, 4 « –2 и т.д.

Примеры 1.18 и 1.19 показывают, что множество может быть эквивалентно своему подмножеству. Так, в примере 1.18 BÌ A, а в примере 1.19 A Ì B. И в том, и в другом случае A

Установить эквивалентность множеств, т.е. установить взаимно однозначное соответствие между их элементами можно различными путями. На рис. 1.5 показано, что множества точек двух отрезков [a, b] и [c, d] эквивалентны.

Таким же образом можно установить эквивалентность множеств точек двух интервалов. На рис.1.6 показано, что множества точек любого интервала (a, b) эквивалентно множеству точек всей прямой.

Для установления эквивалентности двух множеств можно применять следующую теорему.

Теорема Бернштейна. Если множество A эквивалентно части множества B, а множество B эквивалентно части множества A, то множества A и B эквивалентны.

Применим теорему Бернштейна для доказательства того, что множество точек любого отрезка эквивалентно множеству точек любого интервала.

Пусть A = [a, b] – произвольный отрезок, а B = (c, d) – произвольный интервал.

Таким образом, выполняются условия теоремы Бернштейна. Поэтому A

Итак, все интервалы, отрезки и вся прямая эквивалентны между собой.

Счетные множества

Определение 1.3. Множество, эквивалентное множеству натуральных чисел N = <1, 2, 3, …, n,…>, называется счетным.

Можно сказать также, что множество счетно, если его элементы можно перенумеровать.

Следующие множества являются счетными.:

Чтобы установить счетность некоторого множества, достаточно указать взаимно однозначное соответствие между элементами данного множества и множества натуральных чисел. Для примера 1.19 взаимно однозначное соответствие устанавливается по следующим правилам: для множества A₁: –n « n; для множества A₂: 2 n « n; для множества A₃: 2n « n; счетность множества A₄ установлена в примере 1.19;

Установить счетность множеств можно также, используя следующие теоремы о счетных множествах (приводятся без доказательств).

Теорема 1. Всякое бесконечное подмножество счетного множества счетно.

Множество A = <3, 6, …, 3n,…> счетно, т.к. A – бесконечное подмножество множества натуральных чисел, A Ì N.

Теорема 2. Объединение конечной или счетной совокупности счетных множеств счетно.

Множество A = <0, 1, …, n,…> неотрицательных целых чисел счетно, множество B = <0, –1, …, –n,…> неположительных целых чисел тоже счетно, поэтому множество всех целых чисел С = АÈB = <…, –n, …– 2, –1, 0, 1, 2, …, n, …> тоже счетно.

Теорема 3. Множество всех рациональных чисел, т.е. чисел вида , где p и q целые числа, счетно.

Геометрический смысл пары (a_k, b_n) – точка на плоскости с рациональными координатами (a_k, b_n). Поэтому можно утверждать, что множество всех точек плоскости с рациональными координатами счетно.

Теорема 6. Множество всех корней многочленов любых степеней с рациональными коэффициентами счетно.

Источник

Математика, которая мне нравится

Математика для школьников и студентов, обучение и образование

2. Эквивалентность множеств. Счетные и несчетные множества

Определение. Мощностью конечного множества называется число элементов в этом множестве.

Обозначение. Мощность множества будем обозначать .

Любые два конечные множества можно сравнивать по их мощности.

Однако для бесконечных множеств такой способ сравнения не подходит (возьмем, например, множество прямоугольников и множество рациональных чисел).

Рассмотрим способ сравнения множеств, применимый как для конечных, так и для бесконечных множеств. Для этого нам понадобится следующее определение.

Определение. Говорят, что между множествами и установлено взаимно однозначное соответствие, если:

1) каждому элементу множества соответствует только один элемент множества ;

2) каждый элемент множества при этом соответствует некоторому элементу множества ;

3) разным элементам множества соответствуют разные элементы множества .

Тогда можно определить и эквивалентные множества:

Определение. Множества и называются эквивалентными или равномощными, если между ними можно установить взаимно однозначное соответствие.

Таким образом, мы имеем теперь возможность сравнивать по количеству элементов как конечные, так и бесконечные множества.

Приведем несколько примеров.

Пример 2. Покажем, что множество натуральных чисел эквивалентно множеству четных положительных чисел. Для этого установим между этими множествами взаимно однозначное соответствие следующим образом:

иначе: каждому элементу поставим в соответствие элемент множества четных положительных чисел.

Так как множество четных положительных чисел является подмножеством множества натуральных чисел, то этот пример показывает, что бесконечное множество может быть эквивалентно своему подмножеству. В случае конечных множеств такая ситуация невозможна: между конечными множествами и можно установить взаимно однозначное соответствие тогда и только тогда, когда .

Пример 3. Покажем, что множество целых чисел эквивалентно множеству натуральных чисел . Для этого установим между этими множествами взаимно однозначное соответствие следующим образом:

иначе: каждому элементу поставим в соответствие элемент , если 0″ title=»Rendered by QuickLaTeX.com» height=»12″ width=»43″ style=»vertical-align: 0px;»/>, и элемент , если множества натуральных чисел.

Определение. Множество называется счетным, если оно эквивалентно множеству натуральных чисел.

Иначе говоря, множество счетно, если все элементы этого множества можно занумеровать. Таким образом, множества четных положительных чисел и множество целых чисел счетны.

Пример 4. Покажем, что множество положительных рациональных чисел счетно. В самом деле, запишем каждое положительное рациональное число в виде несократимой дроби, запишем его в бесконечную таблицу, а затем перенумеруем числа в таблице способом, указанным на рис. 4:

Пример 5. Множества

счетны, а следовательно, эквивалентны. В самом деле, установим взаимно однозначное соответствие следующим образом:

Пример 6. Любой отрезок эквивалентен отрезку . Искомое взаимно однозначное соответствие можно установить как аналитически, например, формулой:

так и геометрически (см. рис. 5):

Пример 7. Установим взаимно однозначное соответствие между точками интервала и точками полуинтервала . Заметим, что множество и множество равны (множества и определены в примере 4; обозначим . Тогда , . Пусть . Если , то поставим ему в соответствие по закону, описанному в примере 4; если же , то поставим ему в соответствие себя: . Таким образом, устанавливается взаимно однозначное соответствие между и . Следовательно, множества и эквивалентны.

В заключение заметим, что не все бесконечные множества являются счетными. Так, например, можно доказать, что множество точек любого отрезка не является счетным.

Задачи.

1. Докажите, что множество рациональных чисел счетно.

2. Докажите, что множества и равномощны.

3. Установите взаимно однозначное соответствие между элементами множеств и .

Комментариев: 2

1 Stas:

Здравствуйте! В одной из книжек МЦНМО по теории множеств дано упражнение доказать, что некоторые свойства отображения эквивалентны. Корректен ли этот вопрос по отношению к свойствам, ведь определение эквивалентности применяется к множествам, а не к свойствам?

Здравствуйте! Вообще говоря, эквивалентными могут быть и свойства, и даже определения. Поэтому, думаю, что вопрос корректен. Вероятно, Вы спрашиваете, считая, что речь идет о конкретном определении, а подразумевается эквивалентность в более общем смысле.

Источник