Доказать что множество открыто

Замкнутые и открытые множества

Одна из основных задач теории точечных множеств — изучение свойств различных типов точечных множеств. Познакомимся с этой теорией на двух примерах и изучим свойства так называемых замкнутых и открытых множеств.

Приведем примеры замкнутых и открытых множеств. Всякий отрезок есть замкнутое множество, а всякий интервал — открытое множество. Несобственные полуинтервалы и замкнуты, а несобственные интервалы и открыты. Вся прямая является одновременно и замкнутым и открытым множеством. Удобно считать пустое множество тоже одновременно замкнутым и открытым. Любое конечное множество точек на прямой замкнуто, так как оно не имеет предельных точек. Множество, состоящее из точек

Наша задача состоит в том, чтобы выяснить, как устроено произвольное замкнутое или открытое множество. Для этого нам понадобится ряд вспомогательных фактов, которые мы примем без доказательства.

1. Пересечение любого числа замкнутых множеств замкнуто.

2. Сумма любого числа открытых множеств есть открытое множество.

3. Если замкнутое множество ограничено сверху, то оно содержит свою верхнюю грань. Аналогично, если замкнутое множество ограничено снизу, то оно содержит свою нижнюю грань.

4. Если множество замкнуто, то его дополнение открыто и обратно.

Предложение 4 показывает, что между замкнутыми и открытыми множествами имеется весьма тесная связь: одни являются дополнениями других. В силу этого достаточно изучить одни замкнутые или одни открытые множества. Знание свойств множеств одного типа позволяет сразу выяснить свойства множеств другого типа. Например, всякое открытое множество получается путем удаления из прямой некоторого замкнутого множества.

В силу предложения 4, отсюда сразу вытекает, что всякое открытое множество на прямой представляет собой не более чем счетную сумму непересекающихся интервалов. В силу предложений 1 и 2, ясно также, что всякое множество, устроенное, как указано выше, действительно является замкнутым (открытым).

Как видно из нижеследующего примера, замкнутые множества могут иметь весьма сложное строение.

Канторово совершенное множество

Рассмотрим некоторые свойства этого множества. Множество замкнуто, так как оно образуется путем удаления из прямой некоторого, множества непересекающихся интервалов. Множество не пусто; во всяком случае в нем содержатся концы всех выброшенных интервалов.

Можно показать, что множество имеет мощность континуума. В частности, отсюда следует, что канторово совершенное множество содержит, кроме концов смежных интервалов, еще и другие точки. Действительно, концы смежных интервалов образуют лишь счетное множество.

Разнообразные типы точечных множеств постоянно встречаются в самых различных разделах математики, и знание их свойств совершенно необходимо при исследовании многих математических проблем. Особенно большое значение имеет теория точечных множеств для математического анализа и топологии.

Исследования Н.Н. Лузина и его учеников показали, что имеется глубокая связь между дескриптивной теорией множеств и математической логикой. Трудности, возникающие при рассмотрении ряда задач дескриптивной теории множеств (в частности, задач об определении мощности тех или иных множеств), являются трудностями логической природы. Напротив, методы математической логики позволяют более глубоко проникнуть в некоторые вопросы дескриптивной теории множеств.

Источник

Математика, физика на «отлично»

Открытые и замкнутые множества

В курсе математического анализа на первом курсе ВУЗов встречается много непонятного и непривычного. Одна из первых таких «новых» тем — это открытые и замкнутые множества. Постараемся дать пояснения по данной тематике.

Перед тем, как приступить к постановке определений и задач, напомним значение используемых обозначений и кванторов :
∈ — принадлежит
∅ — пустое множество
Ε — множество действительных чисел
х* — закреплённая точка
А* — множество граничных точек
: — такое, что
⇒ — следовательно
∀ — для каждого
∃ — существует
U_ε(х) — окрестность х по ε
Uº_ε(х) — проколотая окрестность х по ε

Итак,
Определение 1: Множество М ∈ Ε называется открытым, если для любого у ∈ М найдётся такое ε > 0, что окрестность y по ε строго меньше М
С помощью кванторов определение запишется следующим образом:
М ∈ Ε — открытое, если ∀ у∈М ∃ ε>0 : U_ε(y) Определение 2: Точка x* ∈ E называется граничной точкой множества М, если в любой окрестности точки х содержатся точки как из множества М, так и из его дополнения.
Теперь с помощью кванторов:
х*∈ E — граничная точка, если ∀U_ε(x) ∩ М ≠ ∅ и ∀U_ε(x) ∩ Е\М

Определение 3: Множество называется замкнутым, если ему принадлежат все граничные точки. Пример — отрезок [a, b]

Стоит отметить, что существуют множества, которые одновременно и открытые, и замкнутые. Это, например, всё множество действительных чисел и пустое множество (позднее будет доказано, что это 2 возможных и единственных случая).

Докажем несколько теорем, связанных с открытым и замкнутым множествами.

Теорема 1: Пусть множество А — открытое. Тогда дополнение к множеству А является замкнутым множеством.
Доказательство: Обозначим дополнение множества А как множество В:
В = Е\А
Доказывать будем от противного.
Предположим, что В — незамкнутое. Тогда существует граничная точка х*, которая не принадлежит В, а значит — принадлежит А. По определению граничной точки окрестность х* имеет пересечение как с В, так и с А. Однако с другой стороны х* является внутренней точкой открытого множества А, поэтому вся окрестность точки х* лежит в А. Отсюда делаем вывод, что множества А и В пересекаются не по пустому множеству. Такого быть не может, поэтому наше предположение неверно и В является замкнутым множеством, ч. т. д.
В кванторах доказательство можно записать короче:
Предположим, что В — незамкнутое, тогда:
(1) ∃ х∈А*:х∈A ⇒ ∀U_ε(x) ∩ В ≠ ∅ (определение граничной точки)
(2) ∃ х∈А*:х∈A ⇒ ∀U_ε(x) ⊂ А ≠ ∅ (определение открытоко множества)
Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — замкнутое, ч. т. д.

Теорема 2: Пусть множество А — замкнутое. Тогда дополнение к множеству А является открытым множеством.
Доказательство: Обозначим дополнение множества А как множество В:
В = Е\А
Доказывать будем от противного.
Предположим, что В — замкнутое множество. Тогда любая граничная точка лежит в В. Но так как А — также замкнутое множество, то все граничные точки принадлежат и ему. Однако точка не может одновременно принадлежать множеству и его дополнению. Противоречие. В — открытое множество, ч. т. д.
В кванторах это выглядеть будет следующим образом:
Предположим, что В — замкнутое, тогда:
(1) ∀ х∈А*:х∈A (из условия)
(1) ∀ х∈А*:х∈В (из предположения)
Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — открытое, ч. т. д.

Теорема 3: Пусть множество А — замкнутое и открытое. Тогда А = Е или А = ∅
Доказательство: Начнём записывать подробно, но сразу использую кванторы.
Предположим, что множество С — замкнутое и открытое, причём С ≠ ∅ и С ≠ Е. Тогда очевидно, что С ⊆ Е.
(1) ∃ х∈А*:х∈С ⇒ ∀U_ε(x) ∩ Е\С ≠ ∅ (определение граничной точки, которая принадлежит С)
(2) ∃ х∈А*:х∈A ⇒ ∀U_ε(x) ⊂ В (определение открытого множества С)
Из (1) и (2) следует, что Е\С ∩ С ≠ ∅, но это неверно. Противоречие. С не может быть одновременно и открытым, и замкнутым, ч. т. д.

Математический анализ — это фундаментальная математика, сложная и непривычная для нас. Но надеюсь, что-то стало понятнее после прочтения статьи. В добрый путь!

Источник

Пересечение любого конечного семейства открытых множеств есть открытое множество.

Доказательство.

1) Действительно, если точка а принадлежит объединению открытых множеств, то она принадлежит по крайней мере, одному из этих множеств, которое по условию теоремы является открытым. Значит, ему принадлежит некоторая окрестность О(а) точки а, но тогда эта окрестность принадлежит и объединению всех открытых множеств. Следовательно, точка а является внутренней точкой объединения. Так как а – произвольная точка объединения, то оно состоит лишь из внутренних точек, и, значит, по определению является открытым множеством.

2) Пусть теперь Х – пересечение конечного числа открытых множеств . Если а есть точка множества Х, то она принадлежит каждому из открытых множеств , и, следовательно, является внутренней точкой каждого из открытых множеств. Другими словами, существуют интервалы , которые целиком содержатся соответственно в множествах . Обозначим через наименьшее из чисел . Тогда интервал будет содержаться одновременно во всех интервалах , т.е. будет целиком содержаться и в , и в . и в , т.е. . Отсюда заключаем, что любая точка является внутренней точкой множества Х, т.е. множество Х является открытым.

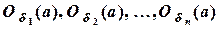
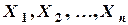
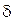
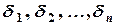
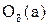
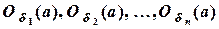
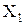
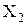
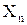
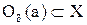
Из этой теоремы следует, что пересечение конечного числа окрестностей точки а есть опять окрестность этой точки. Заметим, что пересечение бесконечного числа открытых множеств не всегда является открытым множеством. Например, пересечением интервалов ,… является множеством, состоящее из одной точки а, которое, не является открытым множеством (почему?).

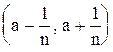
Точка а называется предельной точкой множества Х, если в любой проколотой окрестности 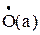этой точки имеется, по крайней мере, одна точка множества Х.

Так, точка является предельной точкой отрезка [0, 1], так как в любом проколотом интервале точки есть точка, принадлежащая этому отрезку. Например, точка , удовлетворяющая неравенству . И таких точек, очевидно, много.

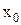
предельные точки множества могут принадлежать ему и могут не принадлежать. Можно доказать, что в любой проколотой окрестности предельной точки а множества Х имеется бесконечно много точек множества Х.

Множество Х называется замкнутым множеством, если оно содержит все свои предельные точки.

Так,всякий отрезок есть замкнутое множество. Интервал (0, 1) не является замкнутым множеством, так как ему не принадлежат две его предельные точки 0 и 1. Множество всех рациональных чисел Q не является замкнутым, так как не содержит некоторые свои предельные точки. В частности, число 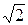является предельной точкой множества Q (докажите!), но Q.

Так как каждая точка множества R является предельной точкой этого множества и принадлежит ему, то R – замкнутое множество.

Пустое множество условимся также считать замкнутым,так как оно содержит все свои предельные точки,которых у него нет.

Всякое конечное множество является замкнутым, так как множество его предельных точек является пустым множеством Æ, которое принадлежит самому множеству.

Теорема:

1) Объединение конечного числа замкнутых множеств есть замкнутое множество;

Источник

§1 определение и примеры метрических пространств

§6. Теоремы об открытых и замкнутых множествах

Теорема 1. Объединение любого числа открытых множеств – множество открытое.

Пусть G k – открытые множества.

Докажем, что – открытое множество.

Получили, что любая точка х о  G – внутренняя, а это означает, что G – открытое множество. 

Пусть G k ( k = 1,2, …, n ) – открытые множества.

Докажем, что – открытое множество.

Замечание 1. Пересечение бесконечного числа открытых множеств может и не быть аоткрытым множеством.

Пусть F k – замкнутые множества.

Докажем, что множества замкнутое, т.е. оно содержит все свои предельные точки.

Теорема 4. Объединение конечного числа замкнутных непустых множеств– замкнутое множество.

Пусть множества F k – замкнутые.

Замечание 2. Объединение бесконечного числа замкнутых множеств может быть множеством открытым.

§7. Последовательности точек метрического пространства

Определение 4. Пусть ( x n ) – последовательность точек метрического пространства ( Х,  ). Точка а  Х называется пределом последовательности ( x n ) если:

Если последовательность ( x n ) имеет конечный предел, то она называется сходящейся, в противном случае – расходящейся.

Обратное не всегда имеет место.

Для сходящихся последовательностей справедливы теоремы.

Теорема 1. Если ( x n ) – сходящаяся последовательность метрического пространства ( Х,  ), то её предел единственный.

§8. Свойства сходящихся последовательностей в некоторых

Теорема 1 ( о покоординатной сходимости последовательности в м. пр. R m ). Для того, чтобы последовательность точек метрического пространства R m

Если выполняются равенства (1), то говорят, что последовательность ( х n ) сходится к точке а покоординатно.

Докажем, что выполняются равенства (1).

В силу равенства (2) (по определению предела последовательности) в м.пр. R m будем иметь:

2. Пусть выполняются равенства (1).

Теорема 2 ( Больцана-Вейерштрасса в м.пр. R m ). Из всякой ограниченной последовательности пространства R m можно выделить сходящуюся подпоследовательность.

Чвстный случай этой теоремы для пространства R 1 был доказан на первом курсе.

Докажем с помощью критерия равномерной сходимости.

Известно, что фукциональная последовательность ( x n ) равномерно сходится да предельной фукции х тогда и только тогда, когда

Замечание 1. Поскольку любая норма задает метрику,

то в нормированном пространстве А также можно определить предел последовательности элементов нормированного пространства.

§9. Полные метрические пространства

Примером фундаментальной последовательности является любая сходящаяся последовательность точек метрического пространства.

В пространстве R любая фундаментальная последовательность – сходящаяся. Но для любого м.пр. не всякая фундаментальная последовательность метрического пространства ( Х,  ) сходится в этом пространстве.

Па определению фундаментальной последовательности и определению метрики в пространстве R m

По определению фундаментальной последовательности

Таким образом, мы доказали, что

0 N  N  m,n > N  x ( t )  x n ( t )    t  [ a,b ].

Банохавыми пространствоми, являются пространства:

Примерами гильбертовых пространств являются перечисленные пространства из примеров §4. Предгильбертовое пространство из примера 3 §4 не является полным относительно нормы (2) и поэтому не является гильбертовым.

Источник

Открытое множество

Для просмотра формул ваш браузер должен поддерживать MathML.

Объявления		Последний пост
	Математики, программисты, репетиторов (платформа SapioX)	28.01.2021 12:47
	Число «Пи» рассчитано с рекордной точностью на «бюджетном» компьютере	27.08.2021 22:26
	Senior lecturer in Mathematics Linkoping (Швеция)	04.09.2021 23:16

Да, речь идёт о вещественной прямой. Я доказывала, что любое открытое множество является объединением интервалов с рациональными концами. Но преподавателю это не понравилось.

Вот моё доказательство:
M- открытое множество. Рассмотрим объединение U всех интервалов с рациональными концами, являющихся подмножествами нашего множества. Докажем, что это объединение совпадает со всем множеством. Действительно, если m — какая-то точка из М, то существует интервал (m1,m2) в М, содержащий m (это следует из того, что М — открытое). На любом интервале можно найти рациональную точку. Пусть на (m1, m) — это m3, на (m,m2) — это m4. Тогда точка m покрыта объединением U, а именно, интервалом (m3,m4). Таким образом, мы доказали, что каждая точка m из М покрыта объединением U. Кроме того, как очевидно следует из построения U, никакая точка, не содержащаяся в М, не покрыта U. Значит, U и М совпадают.

Важным следствием из этой теоремы является тот факт, что любое открытое множество есть счётное объединение интервалов.

Подскажите, пожалуйста, что делать. Преподаватель сказал, что «объединение U всех интервалов с рациональными концами есть сама вещественная прямая и что U не является подмножеством нашего множества M». Я окончательно запуталась. Заранее спасибо!

Редактировалось 1 раз(а). Последний 16.06.2012 15:42.

Спасибо за помощь! Но на диктофон записать не получится, поскольку там, где я учусь, нельзя с собой брать ни телефоны, ни диктофоны, ни флешки.

Редактировалось 1 раз(а). Последний 16.06.2012 23:05.

Источник