Доказать что множество вещественных чисел несчетно

Несчётность множества вещественных чисел

Чтобы показать несчётность всего множества вещественных чисел, достаточно показать несчётность интервала . [18]

Пусть все числа указанного промежутка уже занумерованы некоторым образом. Тогда их можно выписать в следующем виде:

Здесь a_ij — j-я цифра i-ого числа. Очевидно, что все числа указанного вида действительно принадлежат рассматриваемому промежутку, если только в каждом числе не все цифры сразу являются нулями или девятками.

Далее предлагается рассмотреть следующее число:

Пусть каждая цифра d_i этого числа удовлетворяет следующим трём свойствам:

§

§

§

Такое число действительно существует на указанном промежутке, так как оно является вещественным, не совпадает ни с нулём, ни с единицей, а десятичных цифр достаточно, чтобы третье свойство выполнялось. Кроме этого, x интересно тем фактом, что оно не совпадает ни с одним из чисел x_j, выписанных выше, ведь иначе j-я цифра числа x совпала бы с j-ой цифрой числа x_j. Пришли к противоречию, заключающемуся в том, что как бы числа рассматриваемого промежутка ни были занумерованы, всё равно найдётся число из этого же промежутка, которому не присвоен номер. [18]

Это свидетельствует о том, что множество вещественных чисел не является счётным. Его мощность называется мощностью континуума.

Расширенная числовая прямая (читается «эр с чертой») — множество вещественных чисел , дополненное двумя элементами: (положительная бесконечность) и (отрицательная бесконечность), то есть

Бесконечности и , которые не являются числами в обычном понимании этого слова, также называют бесконечными числами, в отличие от вещественных чисел , называемых конечными числами. При этом для любого вещественного числа по определению полагают выполненными неравенства

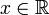
Cледует отличать расширенную числовую прямую от множества вещественных чисел, дополненного одной бесконечностью . Такая система называется проективной прямой, и обозначается

Множество вещественных чисел линейно упорядоченно по отношению . Однако в нет максимального и минимального элементов. Если рассматривать систему вещественных чисел как линейно упорядоченное множество, то ее расширение до системы как раз состоит в добавлении максимального ( ) и минимального ( ) элементов.

Благодаря этому, в системе всякой непустое множество имеет точную верхную грань (конечную, если множество ограничено сверху, и , если не ограничено сверху). Аналогичное утверждение справедливо и для точной нижней грани. Этим объясняется удобство введения элементов и .

Билет 16 вопрос 1

Системное проектирование

К концу 20 века не только существенно возросла сложность проектируемых объектов, но и их воздействие на общество и окружающую среду, тяжкость последствий аварий из-за ошибок разработки и эксплуатации, высокие требования к качеству и цене, сокращению сроков выпуска новой продукции. Необходимость учета этих обстоятельств заставляла вносить изменения в традиционный характер и методологию проектной деятельности.

При создании объектов их уже необходимо было рассматривать в виде систем, то есть комплекса взаимосвязанных внутренних элементов с определенной структурой, широким набором свойств и разнообразными внутренними и внешними связями. Сформировалась новая проектная идеология, получившая название системного проектирования.

Системное проектирование комплексно решает поставленные задачи, принимает во внимание взаимодействие и взаимосвязь отдельных объектов-систем и их частей как между собой, так и с внешней средой, учитывает социально-экономические и экологические последствия их функционирования. Системное проектирование основывается на тщательном совместном рассмотрении объекта проектирования и процесса проектирования, которые в свою очередь включают ещё ряд важных частей, показанных на рисунке 1.

Источник

Множество всех действительных чисел не счетно. Г. Кантор

И тем не менее несчетные множества суще­ствуют. Оказывается, множество всех дейст­вительных чисел — не счетно. Этот заме­чательный факт, как и теорема о счетности множества всех рациональных чисел, впервые в 1874 г. был доказан знаменитым немецким математиком Г. Кантором, основателем современной теории множеств.

Воспроизводим доказательст­во Кантора. Доказываем, что несчетным являет­ся уже множество всех действительных чисел интервала 1 (0; 1).

Каждое такое действительное число может быть записано в виде бесконечной десятичной дроби с целой частью нуль. При этом каждому действительному числу соответствует лишь од­на такая запись, за исключением действительных чисел, выражаемых конечными десятичны­ми дробями: каждое такое число, например 0,2476622021711, может быть записано двумя способами в виде бесконечной десятичной дроби:

Одна из этих записей начиная с некоторого момента содержит одни лишь нули, а другая— одни девятки. Если мы согласимся не употреблять записей, в которых, начиная с какого-нибудь места, идут одни девятки, то каждое действительное число будет иметь лишь един­ственную запись в виде бесконечной десятич­ной дроби. Докажем теперь теорему о несчет­ности множества действительных чисел от про­тивного: предположим, что множество дей­ствительных чисел [мы говорим все время о чис­лах X интервала (0 ; 1)] счетно, т.е. может быть занумеровано посредством натуральных чисел. Тогда вся совокупность действительных чисел интервала (0 ; 1) может быть записана в виде последовательности: х₁, х₂. Запишем разложение числа x_n в бесконечную десятичную дробь в виде:

суть последовательные десятичные знаки числа x_n, причем, согласно заключенному нами условию, не может слу­читься, что все десятичные знаки начиная с некоторого суть девятки. Итак, все действительные числа х [интерва­ла (0; 1)] предполагаются записанными в виде:
Табл: I

Приведем наше предположение к противоре­чию, найдя действительное число с, заклю­ченное между 0 и 1 и заведомо не входящее в табл. I. Для этого рассмотрим цифры, стоя­щие по диагонали в табл. I, а именно:

и выберем для каждого n натуральное число b_n, не превосходящее число 8 и отличное от числа a ( n) _n (например, при а ( n) _n (n) _n=8 полагаем b_n=7). Рассмотрим бесконечную десятичную дробь

то на n-м месте в разложении числа с мы должны были бы иметь цифру

тогда как действительно имеем

1 Под интервалом (а; b) числовой прямой понимает­ся множество всех действительных чисел х, удовлет­воряющих неравенству а

Источник

Пронумеровать все действительные числа на отрезке [0,1]

В качестве доказательства несчетности действительных чисел во всех учебниках по теории множеств приводится так называемый диагональный метод Кантора (подробнее можно ознакомиться в книге «Что такое математика?», авторы Курант, Роббинс, §4. Математический анализ бесконечного. 2. Счетность множества рациональных чисел и несчетность
континуума.). Данный метод доказывает несчетность подмножества действительных чисел, принадлежащих диапазону [0,1]. Однако, если присмотреться к доказательству, становится ясно, что оно не учитывает экспоненциальный рост возможных вариантов с каждым увеличиеним порядкового номера в десятичной дроби.

Кантор рассуждает следующим образом (но только в отношении бесконечных десятичных дробей): расположем десятичные дроби произвольным образом в виде списка, далее пронумеруем их и рассмотрим диагональ. Если к каждой цифре на диагонали прибавить 1, то мы получим число, которого нет в данном списке. Вот как раз таки этот момент на интуитивном уровне вызывает сомнение.

Недостаток диагонального метода

Для того, чтобы понять о чем речь, давайте попробуем рассмотреть идею диагонального метода на следующем примере. Рассмотрим конечные дроби вида: 0,a₁a₂a₃a₄a₅, сформируем из них список так, чтобы получился квадрат размером 5*5, как это показано на рисунке ниже:

Идея моего подхода

Чтобы пронумеровать все действительные числа, принадлежащие диапазону [0, 1], их надо располагать в виде экспоненциально растущего дерева. Рассмотрим десятичные дроби, записанные в двоичной системе. Пусть k – количество знаков после запятой, n – размер алфавита системы счисления. Тогда количество возможных вариантов дробей начиная с k=1 и до ∞ будет функцией от k, это видно на рисунке ниже:

Назовем каждую строку в вышеприведенной таблице – уровнем. Таким образом k – это и номер уровня, и количество знаков после запятой одновременно.

Введем два порядковых номера:

Каждая отдельная цифра в позиции десятичного числа располагается в отдельной ячейке. Напротив каждой такой цифры записываем 2 индекса C и L следующим образом: N C L, где N – значение цифры.

Cтановится очевидно, что С и L – это функции от k и цифр самого числа N: С = fC(k; N), L = fL(k; N). Также становится очевидно, что мы можем пронумеровать все числа из диапазона [0,1], т.к. мы последовательно проходим по каждому уровню и последовательно нумеруем все возможные комбинации на данном уровне.

Осталось вывести аналитическую зависимость для счетчиков C = f C (N) и L = f L (k;N).

Для удобства обозначим L(k;N) как L_k.
Будем считать, что L₀ — 1 = 0.

Если внимательно изучить таблицу, то вырисовывается следующая закономерность:
L_k = (L_k-1 — 1)*S + N + 1,
где k >= 1, N – текущая цифра в дроби, S = |<0,1>| = 2 – размер алфавита двоичной системы счисления. Запись |A| означает мощность множества A, для конечного множества – это количество элементов в нем.

Очевидно, что C содержит сумму всех комбинаций для всех предыдущих уровней плюс L числа для текущего уровня, т.е. C(N) = Σ_i∈[1,k-1]2 i + L(k; N).

Примеры

Рассмотрим произвольное число 0,0101. Его порядковый номер C(0,0101) = 2 1 + 2 2 + 2 3 + L₄ = 2 + 4 + 8 + 6 = 20.

Рассмотрим произвольное число 0,1001. Его порядковый номер C(0,1001) = 2 1 + 2 2 + 2 3 + L₄ = 2 + 4 + 8 + 10 = 24.
L₁ = (L₀ — 1)*2 + 1 + 1 = 0*2 + 1 + 1 = 2
L₂ = (L₁ — 1)*2 + 0 + 1 = (1 — 1)*2 + 0 + 1 = 3
L₃ = (L₂ — 1)*2 + 0 + 1 = (2 — 1)*2 + 0 + 1 = 5
L₄ = (L₃ — 1)*2 + 1 + 1 = (3 — 1)*2 + 1 + 1 = 10

Выводы

Таким образом мы получили алгоритм, который последовательно нумерует абсолютно все действительные числа из диапазона [0,1], при этом, если взять произвольную десятичную дробь произвольной длины, то мы можем вычислить ее уникальный прядковый номер.

Источник

1.21 Несчетные множества

Мы рассмотрели счетные множества. Примеры их можно про­должить. Кроме того, как мы показали, сумма конечного числа или счетного числа счетных множеств есть снова счетное множество. Есте­ственно возникает вопрос: «а существуют ли вообще несчетные мно­жества?». Положительный ответ на него дает следующая теорема:

Множество действительных чисел, заключенных между 0 и 1, несчетно.

Множество действительных чисел D включает в себя множество R рациональных чисел и множество Q иррациональных чисел. Любое иррациональное число можно представить бесконечной непериоди­ческой десятичной дробью.

Множество R – счетное, если мы докажем, что множество Q – несчетное, то несчетным будет и множество D.

Где Аij – J-я десятичная цифра числа AI.

Построим десятичную дробь

С помощью Диагональной процедуры Кантора, а именно: за B1 примем произвольную цифру, не совпадающую с А11; за B2 – произ­вольную цифру, не совпадающую с А22, и т. д. Вообще за BN примем произвольную цифру, не совпадающую с AMn. Построенная таким образом дробь b не совпадает ни с одной дробью a. От a1 она отли­чается по крайней мере первой цифрой, от a2 – по крайней мере второй цифрой и т. д.

Таким образом, никакое счетное множество иррациональных (действительных) чисел, лежащих на отрезке [0; 1], не исчерпывают этого отрезка. Следовательно, множество иррациональных чисел и мно­жество действительных чисел на отрезке [0; 1] является несчетным.

Любые множества, эквивалентные отрезку [0; 1], являются Несчетными:

1. Множество всех точек любого отрезка [ А; B ].

2. Множество всех точек прямой.

3. Множество всех прямых на плоскости.

4. Множество всех непрерывных функций одной или нескольких переменных и т. д.

Источник

Как вообразить несчетное множество?

Как известно, бесконечности бывают разных типов. Бывают счетные, бывают несчетные. Несчетные делятся на множества мощности континуум и все остальные. Счетные множества это такие, элементы которых можно упорядочить в длинный ряд и занумеровать натуральными числами. С несчетными такой фокус не удается. Тогда как же можно представить несчетное множество, в частности множество вещественных чисел [0;1)? Ответ — дерево бесконечной высоты.

Для меня несчетные множества всегда выглядели как непонятное, туманное облако символов витающее где-то на задворках мозга. Но вот недавно
облако скондесировалось в пару не слишком аккуратных, но компактных кристаллов. О них собственно и речь.
Чтобы избежать путаницы, под несчетным множеством будем подразумевать множество мощности континуум (к таким относятся вещественные числа, иррациональные числа, множество всех подмножеств натуральных чисел и другие).

Карусель

Как известно из википедии и других достоверных источников, мощность вещественных чисел отрезка [0;1) является континуумом. Вещественные числа из этого отрезка нельзя посчитать натуральными числами, т.е. сделать так чтобы одному натуральному числу соответствовало одно вещественное и наоборот. Для неверующих проведем диагональную процедуру Кантора.

Представим чисела отрезка [0,1) в двоичной системе счисления и получим набор бесконечных последовательностей единиц и нулей.

Допустим, мы упорядочили такой набор в виде бесконечного списка как на рисунке. Упорядочив, получим квадратную таблицу в каждой ячейке которой находится либо 1, либо 0. Рассмотрим ячейки располагающиеса на главной диагонали.

Инвертировав диагональ(000010. ) получим последовательность не попадающую в наш список, так как полученная последовательнось отличается от каждой попавшей в список хотя бы одним элементом. Последовательность номер n будет отличаться от диагональной в n-ой позиции. Следовательно, диагональная последовательность отсутствует в списке.

Исходя из приведенной схемы несчетное множество можно представлять в виде непрерывногенерируемых последовательностей. Инвертировали одну диагональную последовательность — вставили её в начало списка — сгенерировали новую и так далее. Такая карусель выглядит сомнительно.

Дерево

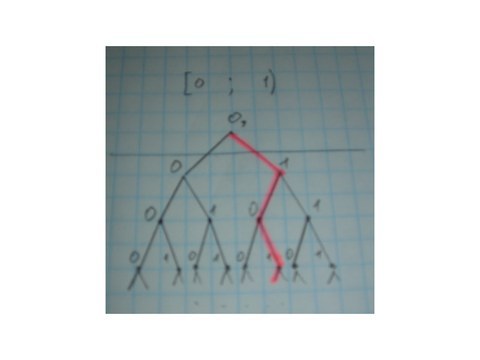
Получается, множество максимальных путей в бинарном дереве бесконечной высоты имеет мощность континуум, что эквивалентно мощности вещественных чисел отрезка [0;1).

Если вернуться к интерпретации бинарных последовательностей как двоичных дробей, то рациональные дроби вида 0,x(y) будут выглядеть в виде конечной кривулины х и бесконечной последовательности кривулин y, иррациональные числа будут выглядеть как одна бесконечная неповторяющаяся кривулина x.

Смешная загогулина

В полученном результате есть одна загвоздка: Количество путей максимальной длинны, исходящих из корня двоичного дерева бесконечной высоты несчетно. Количество же вершин такого дерева можно посчитать. Это легко сделать последовательно нумеруя вершины сверху вниз.

Для дерева конечной высоты расклад другой:
Количество путей максимальной длинны, исходящих из корня в двоичном дереве высотой N равно 2^(N-1), а количество вершин почти в два раза больше — 2^N — 1. Устремляя N к бесконечности получим, что счетная бесконечность вершин в два раза “больше” несчетной бесконечности путей.
Вот такой псевдопарадокс, иллюстрирующий работу интуиции.

Источник