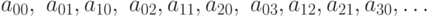Доказать что множество всех конечных подмножеств счетного множества счетно

Счетные множества

Множество называется счетным, если оно равномощно множеству 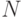натуральных чисел, то есть если его можно представить в виде (здесь — элемент, соответствующий числу ; соответствие взаимно однозначно, так что все различны).

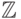
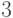
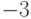
Например, множество целых чисел счетно, так как целые числа можно расположить в последовательность , , , , , , ,

(а) Подмножество счетного множества конечно или счетно.

(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.

(а) Пусть — подмножество счетного множества . Выбросим из последовательности те члены, которые не принадлежат (сохраняя порядок оставшихся). Тогда оставшиеся члены образуют либо конечную последовательность (и тогда конечно), либо бесконечную (и тогда счетно).

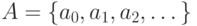
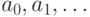
(в) Пусть имеется счетное число счетных множеств Расположив элементы каждого из них слева направо в последовательность ( ) и поместив эти последовательности друг под другом, получим таблицу

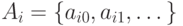
Замечание. В доказательстве утверждения (б) теоремы 2 есть тонкий момент: на каждом шаге мы должны выбрать один из оставшихся элементов множества ; такие элементы есть, но у нас нет никакого правила, позволяющего такой выбор описать. При более формальном построении теории множеств тут нужно сослаться на специальную аксиому, называемую аксиомой выбора. Законность этой аксиомы вызывала большие споры в начале 20-го века, но постепенно к ней привыкли, и эти споры сейчас почти не воспринимаются. В середине века великий логик Курт Гедель доказал, что аксиому выбора нельзя опровергнуть, пользуясь остальными аксиомами теории множеств, а в 1960-е годы американский математик Пол Дж.Коэн доказал, что ее нельзя и вывести из остальных аксиом. (Конечно, понимание этих утверждений требует подробного изложения теории множеств как аксиоматической теории.)

30. Такой же тонкий момент (хотя и менее очевидный) есть и в доказательстве утверждения (в). Можете ли вы догадаться, где он? (Ответ: мы знаем, что множества счетны, то есть что существует взаимно однозначное соответствие между и . Но нужно выбрать и фиксировать эти соответствия, прежде чем удастся построить соответствие между объединением всех и .)

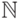
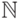
Еще несколько примеров счетных множеств:

31. Докажите, что любое семейство непересекающихся интервалов на прямой конечно или счетно. (Указание: в каждом интервале найдется рациональная точка.)

33. Докажите, что множество точек строгого локального максимума любой функции действительного аргумента конечно или счетно.

Докажите, что множество точек разрыва неубывающей функции Действительного аргумента конечно или счетно.

Источник

06. Теоремы о счетных множествах. Множества мощности континуум

Если рассмотреть любое конечное множество и любое его собственное (непустое и не совпадающее с ним самим) подмножество, то элементов в подмножестве меньше, чем в сам множестве, т. е. часть меньше целого.

Обладают ли бесконечные множества таким свойством? И может ли иметь смысл утверждение, что в одном бесконечном множестве «меньше» элементов, чем в другом, тоже бесконечном? Ведь про два бесконечных множества мы можем пока только сказать, эквивалентны они или нет. А существуют ли вообще неэквивалентные бесконечные множества?

Приведём забавную фантастическую историю из книги Н. Я. Виленкина «Рассказы о множествах». Действие происходит в далёком будущем, когда жители разных галактик могут встречаться друг с другом. Поэтому для всех путешествующих по космосу построена огромная гостиница, протянувшаяся через несколько галактик.

В этой гостинице бесконечно много номеров (комнат), но, как и положено, все комнаты пронумерованы, и для любого Натурального числа n есть комната с этим номером.

Однажды в этой гостинице проходил съезд космозоологов, в котором участвовали представители всех галактик. Так как галактик тоже бесконечное множество, все места в гостинице оказались занятыми. Но в это время к директору гостиницы приехал его друг и попросил поселить его в эту гостиницу.

«После некоторых размышлений директор обратился к администратору и сказал:

– Куда же я дену жильца этого номера? – удивлённо спросил администратор.

– А его переселите в № 2. Жильца же из № 2 отправьте в № 3, из № 3 – в № 4 и т. д.»

Вообще, пусть постоялец, живущий в номере K, переедет в номер K+1, как это показано на следующем рисунке:

Тогда у каждого снова будет свой номер, а № 1 освободится.

Таким образом, нового гостя удалось поселить – именно потому, что номеров в гостинице бесконечно много.

Первоначально участники съезда занимали все номера гостиницы, следовательно, между множеством космозоологов и множеством N Было установлено взаимно однозначное соответствие: каждому космозоологу дали по номеру, на двери которого написано соответствующее ему натуральное число. Естественно считать, что делегатов было «столько же», сколько имеется натуральных чисел. Но приехал ещё один человек, его тоже поселили, и количество проживающих увеличилось на 1. Но их снова осталось «столько же», сколько и натуральных чисел: ведь все поместились в гостиницу!

Мы пришли к удивительному выводу: если к множеству, которое равномощно N, добавить ещё один элемент, получится множество, которое снова равномощно N. Но ведь совершенно ясно, что делегаты-космозоологи представляют собой часть того множества людей, которые разместились в гостинице после приезда нового гостя. Значит, в этом случае часть не «меньше» целого, а «равна» целому!

Итак, из определения эквивалентности (которое не приводит ни к каким странностям в случае конечных множеств) следует, что часть бесконечного множества может быть эквивалентна всему множеству.

Новый постоялец не удивился, когда на другое утро ему предложили переселиться в № 1000000. Просто в гостиницу прибыли запоздавшие космозоологи из галактики ВСК-3472, и надо было разместить ещё 999999 жильцов.

Эта задача оказалась весьма сложной. Но и в этом случае нашёлся выход.

«В первую очередь администратор приказал переселить жильца из № 1 в № 2.

– А жильца из № 2 переселите в № 4, из № 3 – в № 6, вообще, из номера N – в номер 2n.

Определение. Множество А, равномощное множеству натуральных чисел N, называется Счетным множеством (имеет мощность счетного множества). Если множество В является бесконечным и не равномощно множеству N, то его называют несчетным.

Множество, которое является конечным или счетным, еще называют не более чем счетным .

Пусть множество А является счетным. По определению, тогда существует биекция А на N, т. е. каждому аÎА соответствует единственный номер nÎN и множество А обращается в некоторую последовательность <аn>.

Теорема 1. Любое подмножество счетного множества не более чем счетно.

Доказательство. Пусть А = — счетное множество и В Í А. Если В конечное множество, то утверждение доказано. Предположим, что В бесконечное множество. Те элементы А, которые попали в В будут иметь некоторые номера в порядке возрастания: . Тогда необходимая нам биекция, показывающая, что В является счетным множеством, задается в виде: ® k.

Теорема 2. Объединение конечного или счетного числа счетных множеств является счетным множеством.

Теорема 3. Любое бесконечное множество содержит счетное подмножество.

Доказательство. Выберем в заданном множестве А какой-либо элемент, придав ему единичный индекс: а1. Среди всех оставшихся элементов множества А найдется не равный а1 элемент (в силу бесконечности А). Его мы обозначим через а2. Продолжая этот процесс до бесконечности мы получим необходимое нам счетное множество .

Доказательство. Пусть множество М – А не более чем счетно. Тогда множество М = АÈ(М – А) по теореме 2 не более чем счетно. Это противоречит тому, что множество М несчетно и, следовательно, наше исходное предположение не верно. Таким образом, множество М – А несчетно. Последнее еще не означает равномощности множеств М и М – А. Докажем ее. Выделим из М – А счетное множество В. Обозначим через С множество С = (М – А) – В. Справедливы равенства М = АÈВÈС и М – А = ВÈС. Множество АÈВ счетно (теорема 2). Следовательно, существует биекция f из АÈВ на А. Теперь можно построить биекцию g из М на М – А по правилу:

Теорема 5. Если множество С бесконечно, а В не более чем счетно, то множество ВÈС равномощно множеству С.

Доказательство. Если множество С счетно, то множество ВÈС также счетно и следовательно они равномощны. Если же множество С не счетно, то мы можем воспользоваться теоремой 4, положив в ней А = СÇВ, а М = С.

Теорема 6. Если множество С является бесконечным, то существует его подмножество В такое, что В¹С и В равномощно с С.

Доказательство. По теореме 3 мы можем выделить из множества С его счетное подмножество А. Если множество С счетно, то в качестве В из утверждения теоремы можно взять В=А. Если же С не счетно, то можно положить В=С-А и утверждаемое вытекает из теоремы 4.

Теорема 7. Множество рациональных чисел Q является счетным.

Доказательство. Обозначим через Р множество всех пар натуральных чисел (p, q), таких что p и q не имеют общих целых делителей, кроме единицы. Для пары натуральных чисел (p, q) введем ее высоту m = p + q. Обозначим Рn множество пар натуральных чисел высоты n. Нетрудно проверить, что каждое множество Рn является конечным и содержит не более, чем n-1 член. Так как Р = Èn Рn, то множество Р счетно в силу теоремы 2.

Теорема 8. Множество точек интервала (0,1) является несчетным.

Доказательство (Диагональный метод Кантора). Доказательство проведем от противного, предположив, что множество точек интервала (0,1) является счетным. Тогда все точки можно записать в виде последовательности:

Множества, равномощные множеству точек интервала (0, 1), называются множествами мощности Континуум .

Задачи.

1. Показать, что если множества А и В являются счетными, то и их произведение А´В является счетным.

2. Установить биекцию между множеством N всех натуральных чисел и множеством Q всех четных положительных чисел.

3. Установить биекцию между множеством N всех натуральных чисел и множеством Р всех четных чисел.

Источник

Счетные множества

Множество называется счетным, если оно равномощно множеству 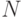натуральных чисел, то есть если его можно представить в виде (здесь — элемент, соответствующий числу ; соответствие взаимно однозначно, так что все различны).

Например, множество целых чисел 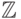счетно, так как целые числа можно расположить в последовательность , , , , , , ,

(а) Подмножество счетного множества конечно или счетно.

(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.

(а) Пусть — подмножество счетного множества . Выбросим из последовательности те члены, которые не принадлежат (сохраняя порядок оставшихся). Тогда оставшиеся члены образуют либо конечную последовательность (и тогда конечно), либо бесконечную (и тогда счетно).

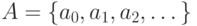
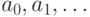
(в) Пусть имеется счетное число счетных множеств Расположив элементы каждого из них слева направо в последовательность ( ) и поместив эти последовательности друг под другом, получим таблицу

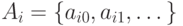
Замечание. В доказательстве утверждения (б) теоремы 2 есть тонкий момент: на каждом шаге мы должны выбрать один из оставшихся элементов множества ; такие элементы есть, но у нас нет никакого правила, позволяющего такой выбор описать. При более формальном построении теории множеств тут нужно сослаться на специальную аксиому, называемую аксиомой выбора. Законность этой аксиомы вызывала большие споры в начале 20-го века, но постепенно к ней привыкли, и эти споры сейчас почти не воспринимаются. В середине века великий логик Курт Гедель доказал, что аксиому выбора нельзя опровергнуть, пользуясь остальными аксиомами теории множеств, а в 1960-е годы американский математик Пол Дж.Коэн доказал, что ее нельзя и вывести из остальных аксиом. (Конечно, понимание этих утверждений требует подробного изложения теории множеств как аксиоматической теории.)

30. Такой же тонкий момент (хотя и менее очевидный) есть и в доказательстве утверждения (в). Можете ли вы догадаться, где он? (Ответ: мы знаем, что множества счетны, то есть что существует взаимно однозначное соответствие между и . Но нужно выбрать и фиксировать эти соответствия, прежде чем удастся построить соответствие между объединением всех и .)

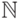
Еще несколько примеров счетных множеств:

31. Докажите, что любое семейство непересекающихся интервалов на прямой конечно или счетно. (Указание: в каждом интервале найдется рациональная точка.)

33. Докажите, что множество точек строгого локального максимума любой функции действительного аргумента конечно или счетно.

Докажите, что множество точек разрыва неубывающей функции Действительного аргумента конечно или счетно.

Источник

Доказать, что множество всех конечных подмножеств счетного множества счётно

Как доказать, что множество всех конечных подмножеств счетного множества счётно?

Мне кажется, можно использовать теорему о том, что объединение счётного числа не более чем счётных множеств не более, чем счётно, но как понять, что всех конечных подмножеств именно счетное множество?

Доказать, что множество счетно
Доказать, что, если множество всех предельных точек множества M \subseteq ^ <1>счётно, то M тоже.

Множество всех подмножеств счетного множества имеет мощность континуума
Тут два варианта: либо помогите с доказательством, либо (что будет еще лучше), направьте на.

Доказать, пользуясь определением мощности, что множество конечных десятичных дробей счетно
Доказать, пользуясь определением мощности, что множество конечных десятичных дробей счетно.

Доказать, что множество счетно
Здравствуйте, если у кого-нибудь есть идеи, то дайте хотя подсказку. Доказать, что множество всех.

Счётно ли множество всех функций f : A → B, если множество A конечно, B — счётно?
Счётно ли множество всех функций f : A → B, если множество A конечно, B — счётно?

Доказать, что множество простых чисел счётно
Как в данном случае строить биекцию между простыми числами и натуральными?

Дано множество. Разработать программу формирования и вывода всех подмножеств данного множества
Дано множество. Разработать программу формирования и вывода всех подмножеств данного множества.

Можно ли утверждать, что множество всех положительных пятизначных чисел счетно
Можно ли утверждать, что множество всех положительных пятизначных чисел счетно? Ответ обосновать

Источник

ТЕОРЕМЫ О СЧЁТНЫХ МНОЖЕСТВАХ

Теорема 1. Любое подмножество счётного множества конечно или счётно. Так как множество счётно, то . Рассмотрим множество . Тогда некоторые из , то есть . Очевидно, это множество конечно или счётно. ■

Теорема 2 (О минимальности счётного множества). Из любого бесконечного множества можно выделить счётное подмножество так, что множество останется бесконечным. . Так как множество бесконечно, то и этот процесс не окончится. Таким образом, мы получим счётное множество и, по крайней мере, счётное множество .■

Теорема 3 (Об идемпотентности). Объединение 1)конечного числа конечных множеств конечно, 2)счётного числа конечных множеств счётно, 3)конечного числа счётных множеств счётно, 4)счётного числа счётных множеств счётно.

■. Доказательство заключается в указании процедуры пересчёта.

1) выписываем все элементы первого множества, потом все элементы второго, не совпадающие с элементами первого и так далее. 2) Множество строим пересчётом например, по следующей схеме: , выбрасывая совпадающие элементы.

3) Пересчёт

проводим, например, по следующей схеме:

4) . Множество строим пересчётом, например, по следующей схеме: , выбрасывая совпадающие элементы. ■

Комментарий. Точно таким же способом пересчёта можно показать счётность множества рациональных чисел, расположив их в виде бесконечной матрицы, выбрасывая совпадающие элементы:

НЕСЧЁТНЫЕ МНОЖЕСТВА

Я возражаю. против употребления актуально

бесконечной величины как чего-либо завершенного,

что никогда не позволительно в математике.

Карл Фридрих Гаусс (1777-1855)

Комментарий. Предыдущие теоремы доказывались установлением биекции между элементами данного множества и элементами множества натуральных чисел. Множество точек отрезка [0, 1] эквивалентно множеству точек отрезка [2,4]; взаимно однозначное соответствие осуществляет, например, функция . Легко установить биекцию между отрезком и всей числовой осью. Это можно сделать, например, в два этапа. Во-первых, с помощью функции устанавливаем биекцию между интервалом и всей числовой осью. Во-вторых, выделим на интервале какую-нибудь последовательность попарно различных точек, например . Точке 0 сопоставим точку , а точке 1 сопоставим точку . Теперь последовательности биективно сопоставляется последовательность , а остальные точки отрезка и интервала соответствуют сами себе. Правило такого сопоставления называется “отелем Гильберта”:

Эту биекцию можно провести иначе. Пусть – это множество точек интервала , согнутого в виде полуокружности, а – это множество точек числовой оси. Тогда между элементами этих множеств легко установить биекцию. Точка –есть пересечение прямой с числовой осью. И, наоборот, взяв любую точку из и, проведя ту самую прямую , мы получим ту единственную точку , которая поставлена в соответствие с .

Таким образом, на любом конечном отрезке и на бесконечной прямой, грубо говоря, “одинаковое число точек”. Более того можно показать, что на любом конечном отрезке и в любом конечномерном пространстве любой размерности тоже “одинаковое число точек”. Проецирование с центром в точке S устанавливает биекцию между точками сферы и плоскости.

Это, кстати, подвергает сомнению понимание размерности пространства, как минимальное число параметров, необходимых для описания положения точки в пространстве. Действительно, рассмотрим точку, принадлежащую единичному квадрату с координатами x=0,a₁a₂a₃… и y=0,b₁b₂b₃… в виде десятичных дробей. Здесь a_i и b_i — цифры в десятичной записи дробей. Сопоставим этой точке точку единичного отрезка с координатой z=0,a₁b₁a₂b₂a₃b₃…(кодировка Кантора).

Ясно, что разным точкам единичного квадрата таким отображением сопоставляются разные точки отрезка. При очевидных уточнениях получаем взаимно однозначное отображение квадрата в отрезок. Совершенно аналогично получается взаимно однозначное отображение -мерного куба в отрезок. Заметим, что существует непрерывное отображение отрезка в квадрат, которое проходит через любую точку квадрата. Оно называется кривой Пеано. Но “количество точек” на отрезке не является счётным.

Разумеемся, прямая не состоит из точек, а плоскость из прямых. Речь идёт о размещении точек на прямой, как воробьёв на ветке. Поэтому выражение “количество точек” на отрезке это эвфемизм, который следует понимать, как количество точек, которые можно поместить на отрезке.

Теорема (Кантора о несчётности точекотрезка ). Множество точек отрезка не счётно. 1. Диагональная процедура Кантора. . Пустьмножество точек отрезка счётно, и все они перечислены: . Построим дробь так, что любая цифра, не содержащая , и так далее. Так как существуют числа, которые могут записывается двояко, например , то не должно содержать цифр 0 и 9. Очевидно, что числа нет в списке всех чисел отрезка , что противоречит условию. ■

. 2. Метод триад Кантора. . Занумеруем все числа отрезка : , а отрезок разобьём на три части. Это равносильно записи числа в троичной системе счисления. Число не попадёт, по крайней мере, в одну из них. Разобьём её на три части. Число не попадёт, по крайней мере, в одну из них. И так далее. В результате получим ССС, то есть существует и единственна точка, принадлежащая всем сегментам сразу. Но её нет в списке всех чисел отрезка по определению. ■

Комментарий. Вспомним начала анализа.

Определение.Если в сегмент вложены сегменты так, что , а , то такая система называется СВС (системой вложенных сегментов).

Определение.Говорят, что (длина сегмента стремится к нулю, при условии, что ), если .

Определение.СВС, у которой называется ССС (системой стягивающих сегментов).

Аксиома Кантора-Дедекинда. В любой СВС существует хоть одна точка, принадлежащая всем им сразу.

Так как рациональные приближения числа можно изобразить системой стягивающихся сегментов, то действительному числу будет соответствовать единственная точка числовой оси, если в системе стягивающих сегментов будетединственная точка, принадлежащая всем им сразу (теорема Кантора). Покажем это.

■. . Пусть и две такие точки, причём , . Так как, , то . Но, с другой стороны, , а, т.е. начиная с некоторого номера , будет меньше любой константы. Это противоречие и доказывает требуемое. ■

Биекция между множеством действительных чисел и числовой осью называется полнотой действительной оси.Утверждение, что на действительной оси “нет дырок” фактически постулируется, то есть является предметом математической веры.

Определение. Мощность несчётного множества точек отрезка называетсямощностью континуума или алеф один.

Примеры. 1. Множество иррациональных чисел несчётно и имеет мощность континуума. Если бы оно было бы счётно, то объединение дух счётных множеств иррациональных и рациональных чисел было бы счётным.

2. Множество всех последовательностей нулей и единиц равномощно множеству всех подмножеств натурального ряда.

■ Сопоставим с каждой последовательностью множество номеров мест, на которых стоят единицы: например, последовательность из одних нулей соответствует пустому множеству, из одних единиц натуральному ряду, а последовательность 10101010. — множеству нечётных чисел. Это множество имеет мощность континуума, так как каждой такой последовательности можно биективно сопоставить дробь , а это двоичное представление действительного числа. То есть множество всех подмножеств натурального ряда, то есть счётного множества, имеет мощность континуума.■

3. Множество бесконечных последовательностей цифр 0, 1, 2, 3

равномощно множеству бесконечных последовательностей цифр 0 и 1, то есть имеет мощность континуума.

■ Закодируем цифры 0, 1, 2, 3 группами 00, 01, 10, 11. Обратное преобразование разбивает последовательность нулей и единиц на пары, после чего каждая пара заменяется на цифру от 0 до 3. ■

4. Множество бесконечных последовательностей цифр
0,1,2 равномощно множеству бесконечных последовательностей цифр 0 и 1, то есть имеет мощность континуума.

■ Закодируем цифры 0, 1 и 2 последовательностями 0, 10 и 11. Теперь всякая последовательность нулей и единиц однозначно разбивается на такие блоки слева направо. ■

5. Доказать, что множество всех бесконечных последовательностей из 0,1,2, в которых 0 и 1 встречаются конечное число раз, счетно.

6. Доказать, что множество точек плоскости, лежащих на графике любой функции, заданной на отрезке [0,1], имеет мощность континуума.

■ Множеству таких точек можно поставить в соответствие множество точек отрезка [0,1], которое имеет мощность континуума. ■

Комментарий. Существуют ли множества с мощностью, большей чем ? Мы показали, что множество всех подмножеств то есть счётного множества с мощностью имеет мощность континуума . Можно ли построить натуральный ряд алефов?

Пример. Покажем, что множество всех действительных функций, непрерывных и нет, имеет мощность, большую, чем .

■. . Пусть существует биекция между точками действительной оси и всеми действительными функциями, то есть . Это фактически означает, что определено множество функций двух переменных . Эти функции определены и при , то есть . Рассмотрим функцию, отличную от неё, например, функцию . В силу биекции, при каком-то . Тогда . Но . То есть . ■

Таким образом, множества с мощностью, большей, чем существуют. Построить их можно, воспользовавшись следующей теоремой.

Теорема 1 (Кантора о больших алефах). Каково бы ни было множество A, множество его подмножеств имеет большую мощность, то есть . ■. Множество эквивалентно части множества , состоящей из одноэлементных подмножеств, то есть . Покажем, что равенство не возможно. . Пусть существует биекция между и подмножеством множества . Сам элемент может как принадлежать , так и нет. Организуем подмножество тех , для которых , то есть . Поскольку существует биекция, то , “представляющее” множество , которое может как принадлежать , так и нет. Пусть . Но в множестве собраны все те элементы , которые не принадлежат своим подмножествам, то есть . Но если , то, так как в множестве собраны все те элементы , которые не принадлежат своим подмножествам, то . Таким образом, множество не существует и биекция невозможна. ■

Комментарий. Страна состоит из округов, каждый из которых имеет депутата в парламенте. Однако он не обязан жить в своём округе. Президент выделил для депутатов, не живущих в своём округе, отдельный округ и обязал всех их переселиться туда. Очевидно, этот округ должен иметь и своего депутата. Но он не может жить ни в самой этой области, ни вне ее.

Теорема 2 (Бернштейна об эквивалентности). Пусть множество эквивалентно некоторому подмножеству множества , а множество эквивалентно некоторому подмножеству множества . Тогда бесконечные множества и эквивалентны, то есть . Пусть множества , а множества . При этом множества , то есть . (см. рис.) Другими словами, и . Теперь множество уже не нужно и требуется доказать, что . Пусть биекцию между множествами и

обеспечивает функция . Тогда , а и так далее. То есть . Таким образом, функция переводит , , то есть . Фактически это множество тех элементов, которые получаются из любого кратным применением , а это множество тех элементов, которые получаются из любого кратным применением . Пересечение всех может быть пусто, а может быть и нет это все элементы, у которых сколь угодно много раз можно находить прообраз. Таким образом, множество разбивается на непересекающиеся слои и “ядро” , причём слои , слои , а на “ядре” функция всё время переставляет элементы между собой. Теперь ясно, как построить биекцию между множеством и множеством . Так как , то достаточно

переместить с помощью функции на место , на место и так далее. Опять работает идея “отеля Гильберта”. Теперь очевидно, что бесконечные множества и эквивалентны. ■

Теперь можно дать определение бесконечному множеству:

Определение (Дедекинд). Множество называют бесконечным, если оно эквивалентно хоть одному собственному подмножеству.

Комментарий. Множества можно рассматривать в двух аспектах: как неупорядоченные и как наделенные некоторым порядком их элементов. Для любых множеств определяется понятие мощности или кардинального числа множества. Для кардинальных чисел (мощностей) строится своя арифметика. Однако чтобы доказывать более тонкие теоремы для бесконечных множеств, понятия множества, лишенного всякой структуры, мало. Для того, чтобы ввести структуру на множестве, его надо арифметизировать, то есть каждому элементу сопоставить некоторую числовую характеристику. Так появляются упорядоченные множества, из которых соответственно и получается обобщение порядковых чисел — трансфинитные ординальныечисла. Каждому ординалу соответствует вполне определенный кардинал, то есть мощность любого вполне упорядоченного множества, которое представляет данный ординал. Сложнее обратное соответствие. Каждое множество определенной мощности можно вполне упорядочить многими способами (бесконечным количеством способов, если оно бесконечно). Поэтому каждому кардиналу соответствует бесконечное множество ординалов, которое Кантор называет числовым классом.

Источник