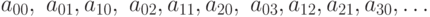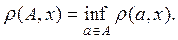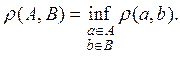Доказать что множество всех многочленов с рациональными коэффициентами счетно

5)F= <(0,0,1,1,1), (0,1,0,1,0), (1,1,1,0, 0)>, не совпадающее с F. Очевидно, что если к множеству (3 ↔ 5) F снова применить ту же операцию при i = 3, j ≠ 5, то получим множество F;

Пример 1.24.

Пусть F= <. Возьмем в качестве элемента а цифру 6. Тогда получим множество R:

Если операцию расширения отношения применить к двум множествам F и Т, используя в качестве элемента а эти же символы F и T, а затем выполнитьоперацию объединения двух получившихся множеств, то получим новое отношение Q, представляющее собой композицию отношений F и Т:

Пример 1.25

Исключив 2-й и 4-й элементы в каждом кортеже множества F= <(а, b, b, с, d), (а, а, b, с, d), (а, с, с, с, d)>, получим новое множество М:

г) удвоение позиции. Пусть F— множество кортежей длины n. Выберем J-ю позицию какого-либо кортежа и повторно запишем находящийся в этой позиции элемент в заранее указанное место в том же кортеже. Тем самым мы выполним операцию удвоения позиции. Условное обозначение этой операции имеет вид D_j F. Выполняется она для каждого кортежа множества F.

Пример 1.26.

Рассмотрим отношение вида:

Допустим, что j-й элемент повторно записывается в каждый кортеж справа. Пусть j = 2, тогда

Рассмотренных операций достаточно для того, чтобы получить представление о том, что является объектом изучения в реляционной алгебре. С другими операциями этой алгебры можно ознакомиться, обратившись к специальной литературе. Например, в некоторых источниках рассмотрена операция конкатенации (расширенного декартова произведения двух отношений).

Источник

Счетные множества

Множество называется счетным, если оно равномощно множеству 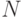натуральных чисел, то есть если его можно представить в виде (здесь — элемент, соответствующий числу ; соответствие взаимно однозначно, так что все различны).

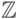
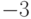
Например, множество целых чисел счетно, так как целые числа можно расположить в последовательность , , , , , , ,

(а) Подмножество счетного множества конечно или счетно.

(в) Объединение конечного или счетного числа конечных или счетных множеств конечно или счетно.

(а) Пусть — подмножество счетного множества . Выбросим из последовательности те члены, которые не принадлежат (сохраняя порядок оставшихся). Тогда оставшиеся члены образуют либо конечную последовательность (и тогда конечно), либо бесконечную (и тогда счетно).

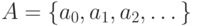
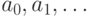
(в) Пусть имеется счетное число счетных множеств Расположив элементы каждого из них слева направо в последовательность ( ) и поместив эти последовательности друг под другом, получим таблицу

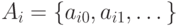
Замечание. В доказательстве утверждения (б) теоремы 2 есть тонкий момент: на каждом шаге мы должны выбрать один из оставшихся элементов множества ; такие элементы есть, но у нас нет никакого правила, позволяющего такой выбор описать. При более формальном построении теории множеств тут нужно сослаться на специальную аксиому, называемую аксиомой выбора. Законность этой аксиомы вызывала большие споры в начале 20-го века, но постепенно к ней привыкли, и эти споры сейчас почти не воспринимаются. В середине века великий логик Курт Гедель доказал, что аксиому выбора нельзя опровергнуть, пользуясь остальными аксиомами теории множеств, а в 1960-е годы американский математик Пол Дж.Коэн доказал, что ее нельзя и вывести из остальных аксиом. (Конечно, понимание этих утверждений требует подробного изложения теории множеств как аксиоматической теории.)

30. Такой же тонкий момент (хотя и менее очевидный) есть и в доказательстве утверждения (в). Можете ли вы догадаться, где он? (Ответ: мы знаем, что множества счетны, то есть что существует взаимно однозначное соответствие между и . Но нужно выбрать и фиксировать эти соответствия, прежде чем удастся построить соответствие между объединением всех и .)

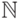
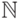
Еще несколько примеров счетных множеств:

31. Докажите, что любое семейство непересекающихся интервалов на прямой конечно или счетно. (Указание: в каждом интервале найдется рациональная точка.)

33. Докажите, что множество точек строгого локального максимума любой функции действительного аргумента конечно или счетно.

Докажите, что множество точек разрыва неубывающей функции Действительного аргумента конечно или счетно.

Источник

Операции с многочленами с рациональными коэффициентами

Эта программа проводит операции с многочленами с целыми коэффициентами, а мне надо переделать её на такую же, но с рациональными коэффициентами. Я пытался эти коэффициенты выражать через двумерный динамический массив, но там я полностью запутался и в итоге ничего не работало. Я веду к тому, что коэффициенты должны выражаться, как числитель поделенный на знаменатель и не совсем понимаю, как это должно выглядить.

Мощность множества всех многочленов с рациональными коэффициентами
Какова мощность множества всех многочленов с рациональными коэффициентами

Многочлены от одного x с рациональными коэффициентами образуют кольцо
Нужно доказать, что многочлены от одного неизвестного с рациональными коэффициентами относительно.

Операции с рациональными дробями
Привет! Пытаюсь сделать задачу. Не понимаю как работать с record. Я так понимаю, что мне нужно.

Операции с рациональными дробями
Даны две дроби a/b и c/d (a, b, c, d– натуральные числа). Составьте программу, в которой в виде.

Решение

Написать программу, которая бы выполняла операции над рациональными дробями
Мне нужно написать программу, которая бы выполняла операции над рациональными дробями: сложение.

Иррациональное число между двумя рациональными
Даны два рациональных числа A и B. Требуется доказать, что между ними есть иррациональное число C.

Корректная работа с огромными рациональными числами.
Здравствуйте Форумчане, как вы считаете, полезно ли будет, если я выложу на форум мой проект.

Задание с многочленами
Не могу понять как решить это задание, так как с математикой у меня не очень. Помогите пожалуйста.

Источник

Следующая теорема устанавливает тесную связь между понятиями точки прикосновения и предельной точки, с одной стороны, и понятием продела — с другой.

Теорема 5. Для того чтобы точка х была точкой прикосновения множества М, необходимо и достаточно, чтобы существовала последовательность 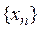точек множества М, сходящаяся к х; для того чтобы точка х была предельной для М — необходимо и достаточно, чтобы существовала сходящаяся к х последовательность, состоящая из попарно различных точек множества М.

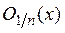
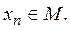
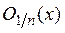
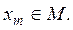
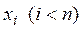
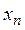
Доказательство. Необходимость. Если x — точка прикосновения множества М, то в каждой ее окрестности содержится хотя бы одна точка Эти точки образуют последовательность, сходящуюся к х. Если точка х — предельная для М, то в каждой окрестности можно найти точку отличную от всех (так как число таких точек конечно). Точки попарно различны и образуют последовательность, сходящуюся к х.

Пусть А и В — два множества в метрическом пространстве R. Множество А называется плотным в В, если 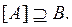В частности, множество А называется всюду плотным (в R), если его замыкание [А] совпадает со всем пространством R. Например, множество рациональных чисел всюду плотно на числовой прямой.

Примеры пространств, имеющих всюду плотное счетное множество[2]. Рассмотрим те же самые примеры, которые указаны в § 8.

1. Пространство, описанное в примере 1 §8, сепарабельно тогда и только тогда, когда оно состоит из счетного числа точек. Это непосредственно вытекает из того, что в этом пространстве [М] = М для любого множества М.

Все пространства, перечисленные в примерах 2-7 § 8, сепарабельны. Укажем в каждом из них по счетному всюду плотному множеству, предоставляя детали доказательств читателю.

2. Рациональные точки.

3. Совокупность векторов с рациональными координатами.

4. Совокупность векторов с рациональными координатами.

5. Совокупность всех многочленов с рациональными коэффициентами.

6. Совокупность последовательностей, в каждой из которых все члены рациональны, и лишь конечное (но произвольное) число их отлично от нуля.

7. Совокупность всех многочленов с рациональными коэффициентами.

Пространство ограниченных последовательностей (пример 8 § 8) не сепарабельно. Действительно, рассмотрим всевозможные последовательности, состоящие из нулей и единиц. Они образуют множество мощности континуума (так как каждую из них можно сопоставить с двоичным разложением некоторого действительного числа, заключенного между 0 и 1). Расстояние между двумя такими точками, определяемое формулой (6) § 8, равно 1. Окружим каждую из этих точек сферой радиуса 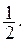Эти сферы не пересекаются. Если некоторое множество всюду плотно в рассматриваемом пространстве, то в каждой из указанных сфер должно содержаться хотя бы по одной точке из этого множества, и, следовательно, оно не может быть счетно.

(1) Пусть А — некоторое множество в метрическом пространстве R и х — точка этого же пространства. Расстоянием от точки х до множества А называется число

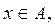
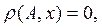
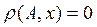
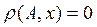
Если то однако из того, что не следует, что Из определения точки прикосновения непосредственно получаем в том и только в том случае, если х есть точка прикосновения множества А.

Таким образом, замыкание [А] множества А может быть определено как совокупность всех тех точек, расстояние которых от множества А равно нулю.

(2) Аналогично можно определить расстояние между двумя множествами. Если А, В — два множества в R, то

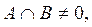
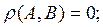
Если то обратное, вообще говоря, неверно.

(3) Если А — множество в метрическом пространство R, то совокупность А’ его предельных точек называется его производным множеством.

В то время как, применяя к [М] еще раз операцию замыкания, мы всегда получим снова [М], равенство (М’)‘ = М’, вообще говоря, не имеет места. Действительно, возьмем, например, множество А точек вида 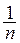на числовой прямой. Его производное множество А’ состоит из единственной точки 0, а множество А» = (А’)‘ будет уже пустым множеством. Если мы рассмотрим на прямой множество В всех точек вида то есть точка 0, а B'» — пустое множество.

Источник

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Мощность всех рациональных функций одного переменного

Найти мощность всех рациональных функций одного переменного.
Решаю эту задачу так: пользуюсь условием, что множество рациональных чисел счетное.
Если представить множество многочленов в виде матрицы, а их коэффициенты будут рациональные, то все возможные варианты одного из коэффициентов составят счетное множество. Далее я пронумерую эти коэффициенты в матрице, значит множество коэффициентов счетное.
Далее я объединяю счетное множество коэфициентов со счетным множеством всех возможных рациональных значений одного коэффициента. Получаю в итоге счетное множество.

Заслуженный участник

Последний раз редактировалось ИСН 20.02.2013, 17:39, всего редактировалось 1 раз.

Заслуженный участник

Заслуженный участник

Последний раз редактировалось gris 20.02.2013, 18:14, всего редактировалось 3 раз(а).

Вообще-то рациональной функцией называют отношение двух многочленов с действительными коэффициентами. Очевидно, что это не подходит к Вашему решению, так как даже множество постоянных функций несчётно.

Если же понимать под рациональной функцией многочлен с рациональными коэффициентами, на что у Вас явный намёк, то идея понятна, но слова «объединение счетного множества коэфициентов со счетным множеством всех возможных рациональных значений одного коэффициента» не имеют отношения к множеству всех многочленов с рациональными коэффициентами или просто невнятно сформуированы.
Лучше подумать о счётном объединении некоторых конечных прямых произведений счётных множеств.

Заслуженный участник

Последний раз редактировалось gris 20.02.2013, 18:29, всего редактировалось 1 раз.

Заслуженный участник

Заслуженный участник

Последний раз редактировалось gris 20.02.2013, 18:57, всего редактировалось 1 раз.

Ну немножко не так. Дело в том, что множество всех непрерывных функций континуально. Впрочем, это же тоже надо доказывать. Наверное, лучше через коэффициенты. Один многочлен или два — никакой разницы. Главное, что рациональная функция задаётся конечным множеством действительных коэффициентов.

Заслуженный участник

Найти мощность всех рациональных функций одного переменного.
Решал эту задачу на контрольной так: решил взять одну из этих рациональных функций , ее мощность континуум, потому что мощность прямой континуум. Так я утверждал, что мощность всех рациональных функций будет не меньше континуума. Но преподаватель сказал, что так нельзя решать задачу.

Решил так сделать: рассматриваю все возможные многочлены, которые конечны. Из их коэффициентов составил матрицу. Так как коэффициенты действительные, то есть там рациональные и ирациональные числа могут быть.
Значит множество всех возможных значений одного коэффициента будет континуум. Далее я помню, что у меня многочлены конечные, значит коэффициенты сами в многочлене я могу пронумеровать, их будет конечное число в этом случае. Теперь самих многочленов бесконечно много, но сами многочлены я тоже могу пронумеровать. Значит, все коэффициенты всех возможных многочленов я могу пронумеровать. Тогда их множество счетное. А множество всех возможных значений одного коэффициента континуум. Тогда получается объединение континуум множеств, число их счетное. Тогда результат будет континуум.

Заслуженный участник

Последний раз редактировалось gris 04.03.2013, 18:35, всего редактировалось 4 раз(а).

Последний раз редактировалось kola1357 04.03.2013, 19:39, всего редактировалось 1 раз.

Вот тут проблема в том, что у нас не было на лекции теорем, с помощью которых можно бы было доказать, что не больше континуума.

Но вот есть такая идея, если получилось доказать, что функции, их множество континуум, то и тоже мощность континуум, как объединение 2-ух континуум множеств, а это тоже континуум. Тогда если возьмем бесконечные многочлены, тогда получается объединение континум множеств, число которых счетно, так как сами коэффициенты мы можем пронумеровать. Тогда мощность одного бесконечного многочлена рациональной функции континуум. Теперь если взять все возможные многочлены, их мощность континнум, так как можно установить взаимно-однозначное соответствие с натуральным рядом. Тогда опять получается объединение счетных множеств, каждое из которых континуум, тоже будет континуум.

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Источник