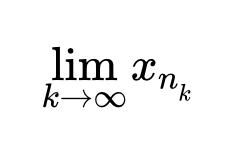Доказать что монотонная последовательность будет сходящейся если сходится ее подпоследовательность

Научный форум dxdy

Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки

Правила форума

Доказать что последовательность сходится (90)

Доказать что монотонная последовательность сходиться, если сходится некоторая ее подпоследовательность.

Дайте подсказу пожалуйста. Не знаю с чего начать

Заслуженный участник

В монотонном случае сходимость равносильна ограниченности. Докажите, что из ограниченности подпоследовательности следует ограниченность всей последовательности.

Можете кратко написать доказательство от противного? а то я пока никак не соображу (

Мой вариант решения.
(1) Каждый элемент подпоследовательности начиная с какого-то номера больше элемента самой последовательности.

(1.1) Допустим что при выкидывании Q элементов последовательности получаеться подпоследовательность P1 каждый элемент которой больше соответствующего элемента последовательности . Докажем
(1.2) что из этого (1.1) следует что при выкидывание Q+1 элемента подпоследовательности P1 получаеться подпоследовательность P2, каждый элемент которой начиная с некоторого номера больше соответствующего элемента в последовательности .

Очевидно что каждый элемент последовательности P2 больше соответствующиего элемента последовательности P1, откуда и следует (1.2)
Доказательство (1) конец.

из (1) и из того что подпоследовательность сходиться следует
что все элементы последовательности меньше верхней грани подпоследовательности. Следовательно последовательность ограничена.

Таким образом получаеться что последовательность ограничена сверху и монотонно возрастает, следовательно последовательность сходится.

Источник

Предел монотонной последовательности

Монотонная последовательность. Точные грани последовательности.

Последовательность \(\\>\) называют возрастающей (неубывающей), если для любого \(n\in\mathbb\) выполняется неравенство
$$
x_\geq x_.\label
$$
Аналогично последовательность\(\\>\) называют убывающей (невозрастающей), если для любого \(n\in\mathbb\) справедливо неравенство
$$
x_\leq x_.\label
$$
Если неравенство \eqref можно записать в виде \(x_>x_\), а неравенство \eqref — в виде \(x_ 0 \ \exists x_<\varepsilon>\in X:x_<\varepsilon>>M-\varepsilon\>.\label
$$
Аналогично определение точной нижней грани \(\displaystyle \inf\) числового множества \(X\) можно записать в виде
$$
\displaystyle \\Leftrightarrow\<\forall x\in X\rightarrow x\geq m\>\wedge\<\forall\varepsilon>0\ \exists x_<\varepsilon>\in X:x_ <\varepsilon>0\ \exists N_<\varepsilon>:x_>>a-\varepsilon\>,\label
$$
$$
[b=\displaystyle \inf\\>]\Leftrightarrow\<\forall n\in N\rightarrow x_\geq b\>\wedge\<\forall\varepsilon 0\) (рис. 6.1) найдется член последовательности, больший \(a-\varepsilon\), то есть
$$
\forall\varepsilon>0 \ \exists N_<\varepsilon>:x_>>a-\varepsilon.\label
$$

Рис. 6.1

Аналогично разъясняется определение \eqref точной нижней грани последовательности.

Признак сходимости монотонной последовательности.

Если последовательность \(\<>\>\) является возрастающей и ограниченной сверху, то существует
$$
\lim_x_=\sup\\>.\nonumber
$$

Если последовательность \(\\>\) является убывающей и ограниченной снизу, то существует
$$
\lim_x_=\inf\\>.\nonumber
$$

\(\circ\) Ограничимся доказательством теоремы для случая ограниченной сверху и возрастающей последовательности.

Если последовательность \(\\>\) ограничена сверху, то есть множество чисел \(x_<2>,x_<2>, \ldots,x_, \ldots\) ограничено сверху, то по теореме о существовании верхней грани существует точная верхняя грань этой последовательности, определяемая условиями \eqref, \eqref. Так как \(\\>\) — возрастающая последовательность, то
$$
\forall n\geq N_<\varepsilon>\rightarrow x_>\leq x_.\label
$$

Из \eqref-\eqref следует, что
$$
\forall\varepsilon>0 \ \exists N_<\varepsilon>:\forall n\geq N_<\varepsilon>\rightarrow a-\varepsilon Замечание 1.

Теорема 1 остается справедливой для последовательности, ограниченной сверху (снизу) и возрастающей (убывающей), начиная с некоторого номера.

Источник

Подпоследовательности и частичные пределы последовательностей

Определение подпоследовательности

Свойства подпоследовательностей

Свойство 3 является следствием свойств 1 и 2.

Частичный предел последовательности

Произвольная последовательность может иметь конечное или бесконечное число частичных пределов ⇑.

5. Свойство частичного предела последовательности
Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.
Доказательство ⇓

Верхний и нижний частичные пределы

Рассмотрим множество частичных пределов последовательности. Эта теорема утверждает, что верхняя и нижняя грани этого множества являются ее элементами. То есть множество частичных пределов последовательности замкнуто, оно содержит свою границу. Для произвольного множества это может не выполняться. Например, для открытого интервала не существует наибольшего и наименьшего элемента, поскольку и верхняя грань b и нижняя a не принадлежит этому множеству.

Если последовательность не ограничена сверху, то ее верхний частичный предел равен плюс бесконечности:
.
Соответственно, если последовательность не ограничена снизу, то
.

Если последовательность ограничена, то ее верхний и нижний частичные пределы конечны.

8. Теорема о неравенстве между верхним и нижним частичными пределами
Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.
Доказательство ⇓

9. Связь верхних и нижних пределов между последовательностями n> и <–x_n>.
Имеет место очевидное равенство:
.

10. Свойства верхних и нижних пределов суммы последовательностей
Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.
Доказательство ⇓

11. Свойство верхних пределов произведения последовательностей
Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.
Доказательство ⇓

Применяя равенство
,
можно получить другие подобные соотношения.

Доказательство свойств и теорем

Далее перечислены определения и свойства, которые мы будем использовать при доказательстве свойств подпоследовательностей.

1. Свойство подпоследовательностей сходящейся последовательности

2. Свойство последовательности, все подпоследовательности которой сходятся к одному числу

5. Свойство частичного предела последовательности

Все свойства ⇑ Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.

Возьмем произвольную окрестность точки a : ⇑. В качестве первого члена подпоследовательности возьмем любой член последовательности, принадлежащий этой окрестности.

6. Теорема о существовании верхнего и нижнего частичных пределов

В этом случае точка является верхним частичным пределом последовательности.

Пусть последовательность ограничена сверху и при этом любой отрезок содержит только конечное число членов последовательности.

Поскольку мы выбирали самые правые отрезки с бесконечным числом членов, то точка c является верхним частичным пределом последовательности.

7. Свойство верхнего и нижнего частичных пределов

8. Теорема о неравенстве между верхним и нижним частичными пределами

Все свойства ⇑ Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.

10. Свойства верхних и нижних пределов суммы последовательностей

Все свойства ⇑ Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.

Докажем второе неравенство:
.
Умножим первое неравенство на – 1 :
.
Применим свойство 8 ⇑:
.

11. Свойство верхних пределов произведения последовательностей

Все свойства ⇑ Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.

Из (10.1) и (10.2) следует, что
.
Свойство доказано.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник